NHP MN PHNG TRNH O HM RING CHNG

NHẬP MÔN PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG

CHƯƠNG 0 Nhắc lại về phương trình vi phân -Phương trình tách biến -Phương trình tuyến tính -Phương trình cấp 2 hệ số hằng -Phương trình cấp 2 tổng quát

CHƯƠNG 1. CHUỖI FOURIER Chuỗi Fourier đầy đủ Chuỗi Fourier sin Chuỗi Fourier cosin Hội tụ và khả vi Thực hành với Matlab

KHAI TRIỂN TAYLOR Một hàm khả vi vô hạn lần có thể khai triển thành dạng chuỗi Taylor quanh điểm x 0 nằm trong khoảng xác định. Dạng như sau: Trong đó:

VÍ DỤ Tìm khai triển Taylor, Maclaurin của hàm số y=sinx trong lân cận của điểm x 0=0

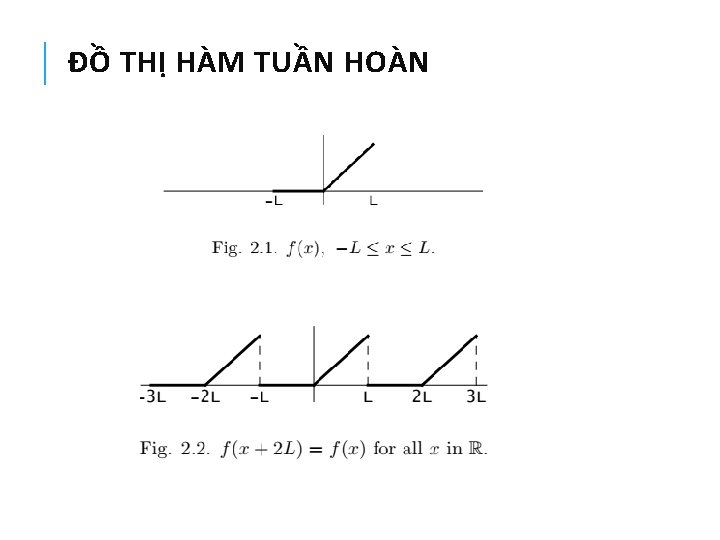
ĐỊNH NGHĨA HÀM TUẦN HOÀN Một hàm số xác định trên R gọi là tuần hoàn nếu tồn tại số T>0 sao cho: Giá trị nhỏ nhất của T gọi là chu kỳ cơ bản hay đơn giản là chu kỳ của hàm f. Dễ thấy nếu f là hàm tuần hoàn với chu kỳ T thì:

ĐỒ THỊ HÀM TUẦN HOÀN

BIỂU DIỄN HÀM TUẦN HOÀN

FOURIER (1976 – 1830)

BIỂU DIỄN FOURIER

BIỂU DIỄN FOURIER – HỆ SỐ a 0 Lấy tích phân hai vế ta có: Vậy hệ số a 0 được xác định bởi công thức:

BIỂU DIỄN FOURIER – HỆ SỐ ai Nhân hai vế với cosnx và lấy tích phân hai vế ta có: Vậy các hệ số ai được xác định bởi công thức:

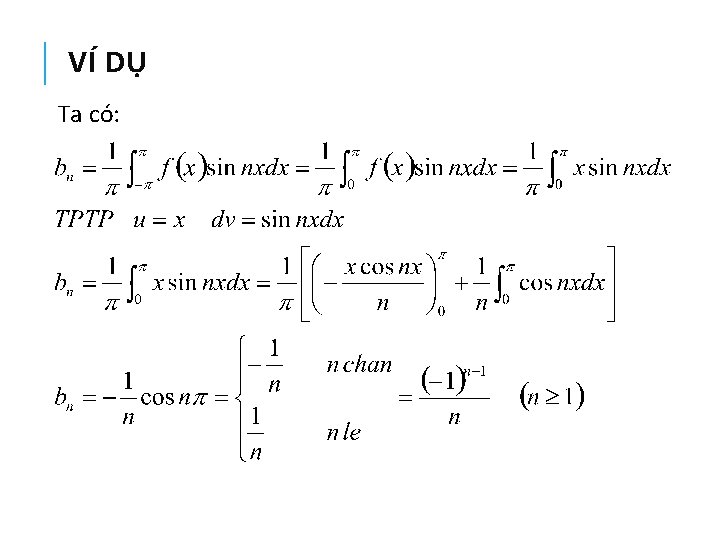
BIỂU DIỄN FOURIER – HỆ SỐ bi Nhân hai vế với sinmx và lấy tích phân hai vế ta có: Vậy các hệ số bi được xác định bởi công thức:

ĐỊNH NGHĨA. CHUỖI FOURIER VÀ HỆ SỐ FOURIER

CHÚ Ý Có thể chuỗi Fourier của một hàm không hội tụ về hàm tại những điểm xác định trong TXĐ của hàm số. Do đó thay vì viết dấu = ta sử dụng ký hiệu sau: Phần sau (mục hội tụ) sẽ nói rõ hơn về vấn đề này. Ta xét chuỗi Fourier của hàm liên tục từng khúc vì nhiều hàm trong ứng dụng chỉ liên tục từng khúc chứ không liên tục.

MỞ RỘNG HÀM

VÍ DỤ Vậy chuỗi Fourier cần tìm:

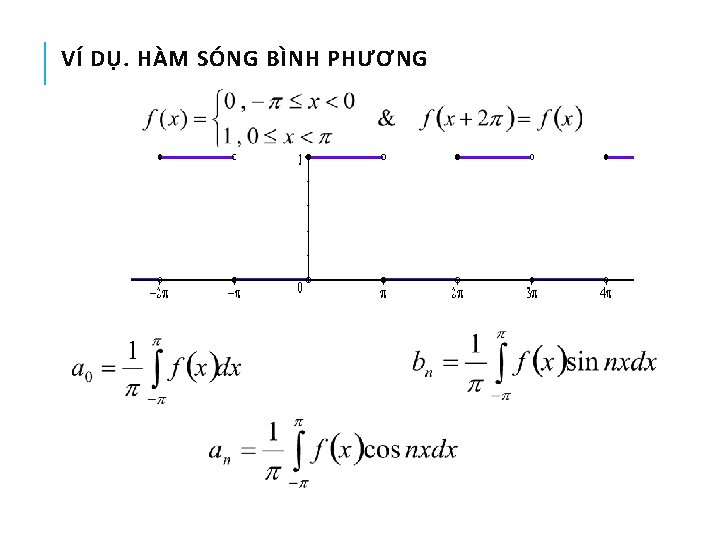
VÍ DỤ. HÀM SÓNG BÌNH PHƯƠNG

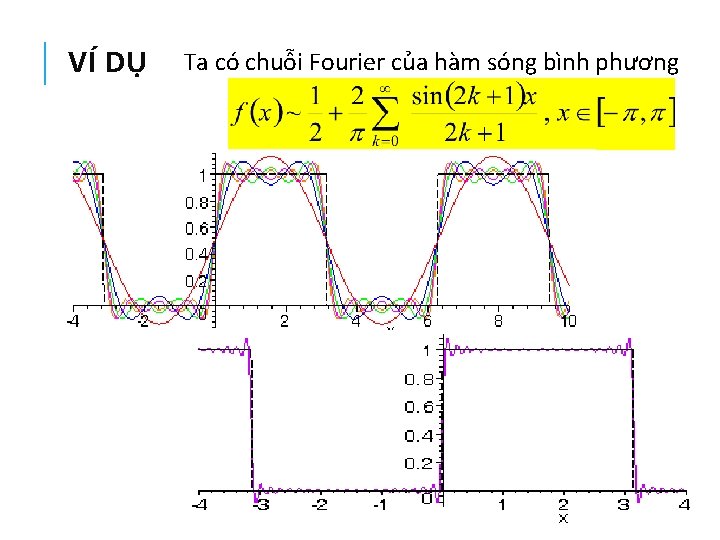
VÍ DỤ Ta có chuỗi Fourier của hàm sóng bình phương

TÍNH CHẤT

BÀI TẬP

CHUỖI FOURIER TỔNG QUÁT (ĐẦY ĐỦ) Xét hàm f(x) liên tục từng khúc và có chu kỳ là P=2 L Ta muốn xây dựng chuỗi Fourier cho hàm này. Đặt hàm g như sau: Dễ thấy:

CHUỖI FOURIER TỔNG QUÁT (ĐẦY ĐỦ) Như vậy hàm g(u) là hàm tuần hoàn với chu kỳ 2 pi. Giả sử có chuỗi Fourier tương ứng Với:

BIẾN ĐỔI Ta có: Trong đó:

ĐỊNH NGHĨA CHUỖI FOURIER VÀ HỆ SỐ FOURIER Cho hàm f(x) liên tục từng khúc và có chu kỳ 2 L xác định với mọi x. Khi đó chuỗi Fourier của hàm f(x) là chuỗi. Trong đó:

TÍNH CHẤT

VÍ DỤ Cho hàm tuần hoàn với chu kỳ P=2 L=4: Đáp án

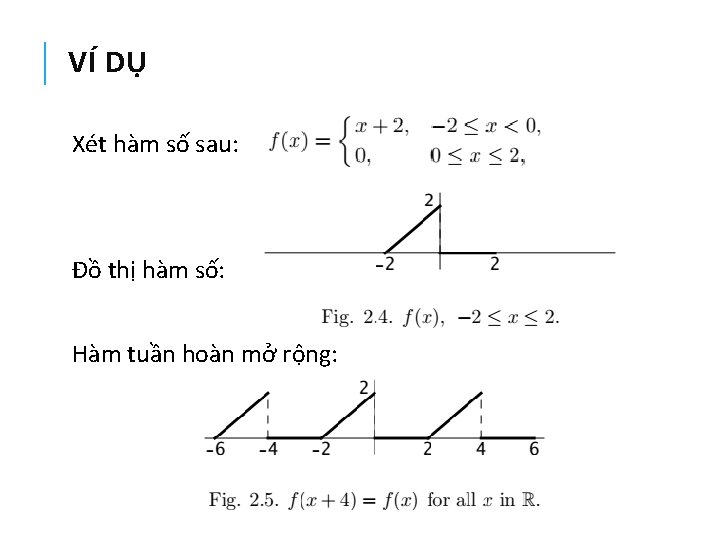
VÍ DỤ Xét hàm số sau: Đồ thị hàm số: Hàm tuần hoàn mở rộng:

TÍNH TOÁN HỆ SỐ FOURIER Ta có: Chuỗi Fourier:

TRÊN TẬP XÁC ĐỊNH HÀM SỐ Như vậy, theo định lý 2. 5, trên [-2, 2] ta có: Chú ý hàm ban đầu có điểm nhảy tại x=0. F(0+)=2 và F(0 -)=0 nên giá trị trung bình là 1.

ĐỊNH LÝ HỘI TỤ là giá trị trung bình các giới hạn trái và phải của hàm f tại điểm x. Chuỗi Fourier của hàm tuần hoàn, trơn từng khúc hội tụ đến giá trị trung bình của hàm số với mọi x.

VÍ DỤ Cho f(x) là hàm chu kỳ 2 với f(x)=x 2 nếu 0<x<2 Nếu x là số nguyên chẵn thì giá trị f(x) xác định bởi: Hãy tìm chuỗi Fourier của hàm này.

VÍ DỤ Đáp án: Nếu thay x=0 ta có: Nếu thay x=1 ta có:

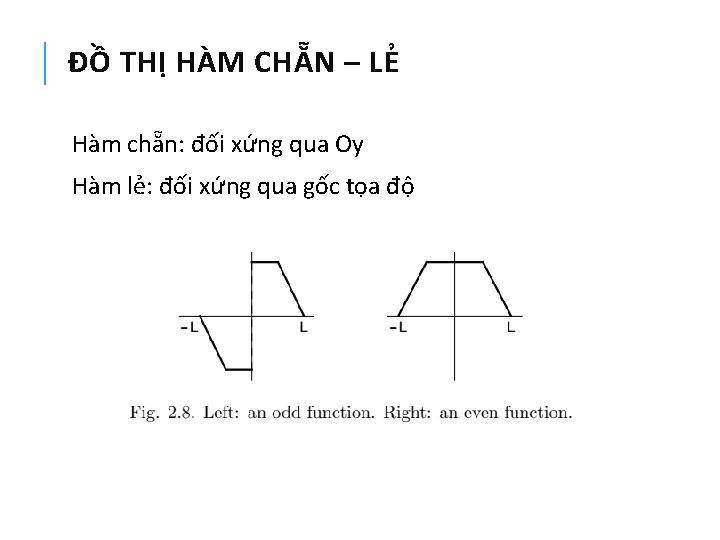
CHUỖI FOURIER SINE VÀ COSINE Hàm chẵn và hàm lẻ Hàm số f(x) xác định với mọi x gọi là chẵn nếu Hàm số f(x) xác định với mọi x gọi là lẻ nếu Tính chất: - Hàm chẵn đối xứng qua Oy - Hàm lẻ đối xứng qua gốc tọa độ O

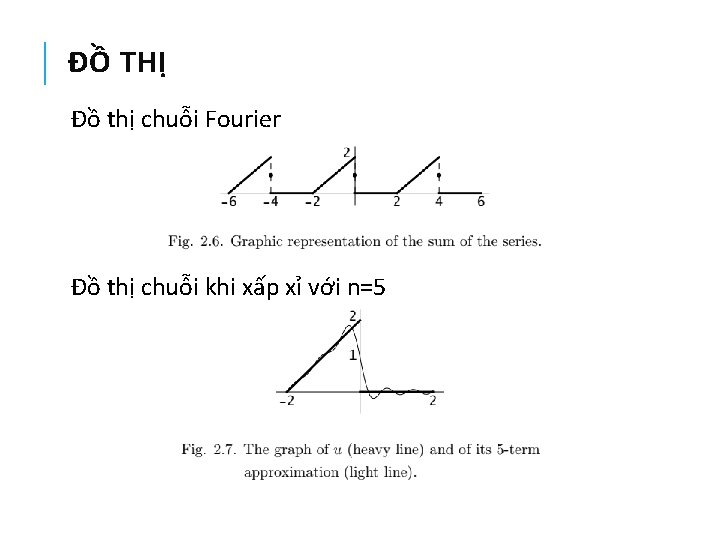
ĐỒ THỊ Đồ thị chuỗi Fourier Đồ thị chuỗi khi xấp xỉ với n=5

ĐỒ THỊ HÀM CHẴN – LẺ Hàm chẵn: đối xứng qua Oy Hàm lẻ: đối xứng qua gốc tọa độ

VÍ DỤ + Tích hai hàm chẵn Hàm chẵn + Tích hai hàm lẻ Hàm chẵn + Tích một hàm chẵn và một hàm lẻ Hàm lẻ + Chuỗi Fourier của các hàm chẵn chỉ gồm các phần tử cosine + Chuỗi Fourier của các hàm lẻ chỉ gồm các phần tử sine

TÍNH CHẤT Nếu f(x) là hàm chẵn và tuần hoàn với chu kỳ 2 L thì: + Hàm: là hàm chẵn + Hàm: là hàm lẻ + Tích phân hàm chẵn, hàm lẻ trên miền đối xứng

TÍCH PH N HÀM CHẴN – LẺ Trên tập xác định đối xứng. Hàm chẵn có tích phân gấp 2 lần trên 1 nửa miền. Hàm lẻ có tích phân bằng 0.

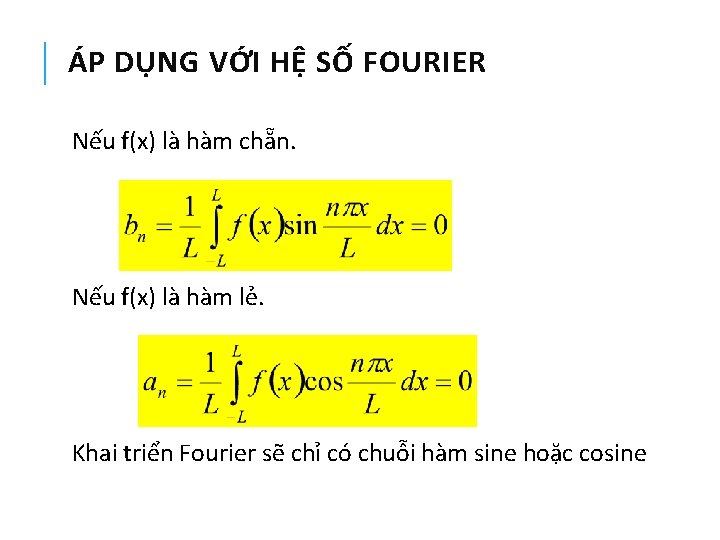
ÁP DỤNG VỚI HỆ SỐ FOURIER Nếu f(x) là hàm chẵn. Nếu f(x) là hàm lẻ. Khai triển Fourier sẽ chỉ có chuỗi hàm sine hoặc cosine

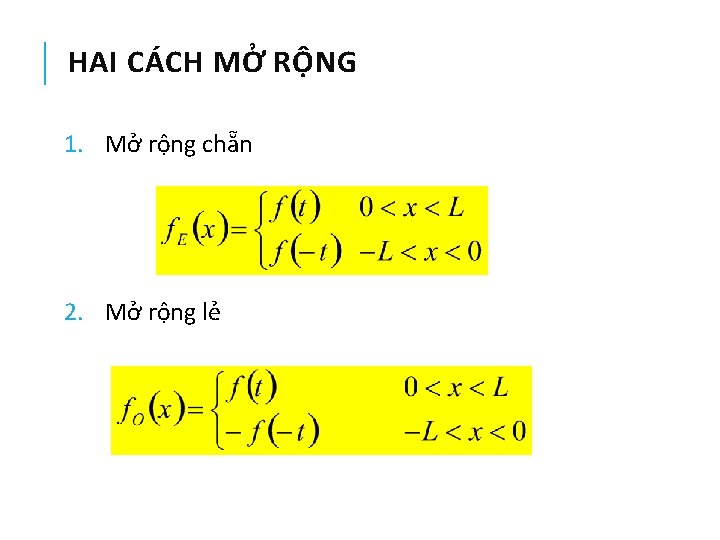
MỞ RỘNG CHẴN VÀ LẺ Nếu hàm số tuần hoàn với mọi t thì chuỗi Fourier xác định duy nhất. Tuy nhiên nếu hàm số chỉ xác định trong khoảng 0<x<L nhưng ta vẫn muốn biểu diễn giá trị hàm này dạng chuỗi hàm Fourier thì? ? ? 1. Mở rộng hàm số ra toàn khoảng (-L, L) tức là mở rộng giá trị hàm số trên (-L, 0) 2. Mở rộng tuần hoàn ra toàn trục số theo công thức 3. Tìm chuỗi Fourier

CHÚ Ý - Với mỗi cách mở rộng trên (-L, 0) khác nhau sẽ cho chuỗi Fourier khác nhau - Các chuỗi đều hội tụ về hàm ban đầu trên (0, L) nhưng sẽ khác nhau trong khoảng (-L, 0) - Ta thường đưa ra các mở rộng tự nhiên: Mở rộng hàm chẵn Mở rộng hàm lẻ

HAI CÁCH MỞ RỘNG 1. Mở rộng chẵn 2. Mở rộng lẻ

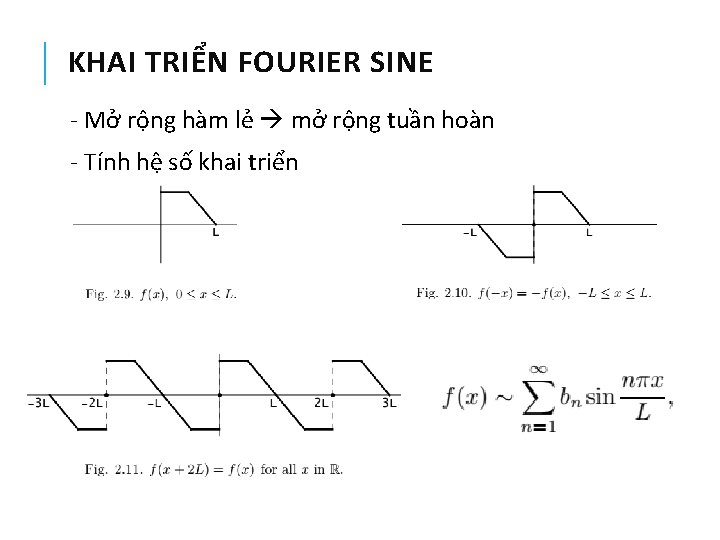
KHAI TRIỂN FOURIER SINE - Mở rộng hàm lẻ mở rộng tuần hoàn - Tính hệ số khai triển

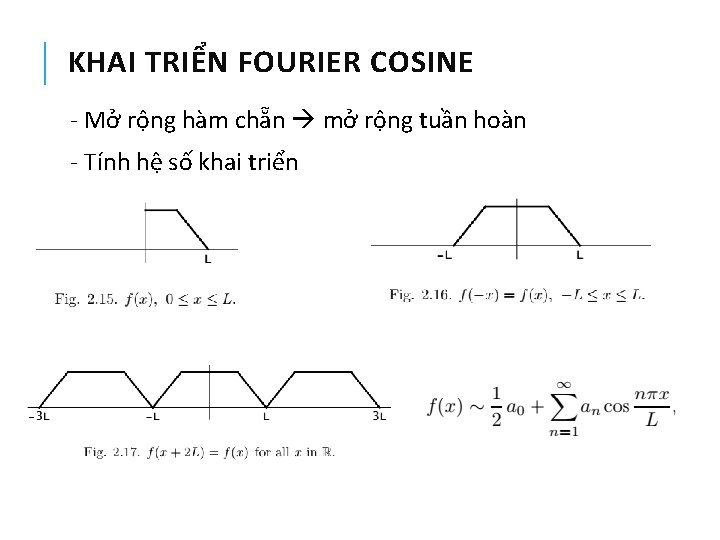
KHAI TRIỂN FOURIER COSINE - Mở rộng hàm chẵn mở rộng tuần hoàn - Tính hệ số khai triển

VÍ DỤ - HÀM CHẴN Khai triển Fourier:

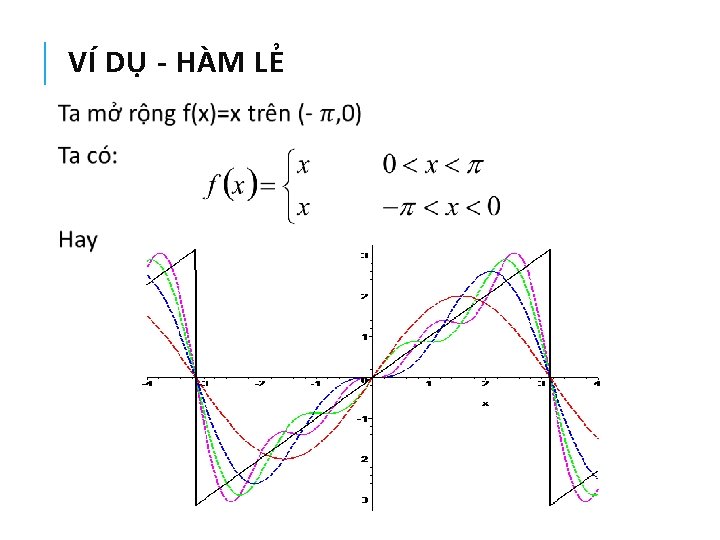
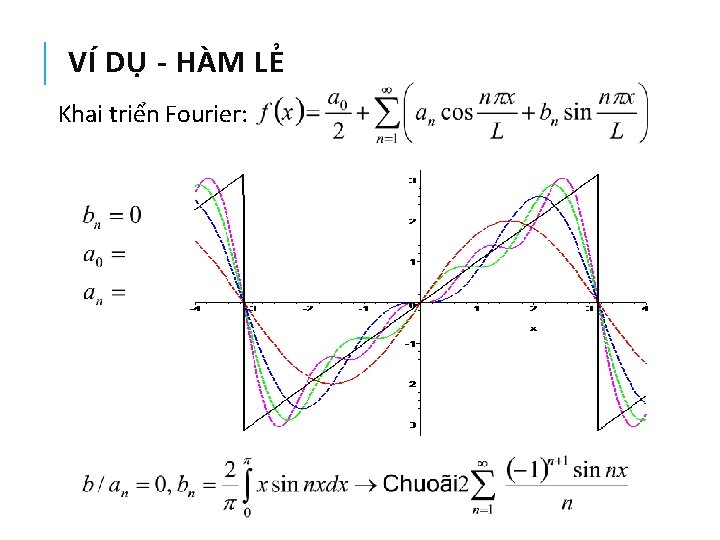
VÍ DỤ - HÀM LẺ Khai triển Fourier:

CHUỖI FOURIER SINE VÀ COSINE Định nghĩa. Giả sử hàm số f(x) liên tục từng khúc trong khoảng [0, L]. Khi đó: Chuỗi Fourier cosine của hàm f là chuỗi: Chuỗi Fourier sine của hàm f là chuỗi:

VI PH N TỪNG PHẦN Định lý. Giả sử hàm số f là liên tục với mọi x, tuần hoàn với chu kỳ 2 L, có đạo hàm là f’ và đạo hàm của nó trơn từng khúc với mọi x. Khi đó, chuỗi Fourier của f’ là chuỗi: Nhận được bằng việc lấy vi phân từng phần chuỗi:

TÍCH PH N TỪNG PHẦN Định lý. Giả sử hàm số f là liên tục với mọi x, tuần hoàn với chu kỳ 2 L và chuỗi Fourier: Có thể không hội tụ. Khi đó: và chuỗi bên vế phải hội tụ với mọi x.

ĐỊNH LÝ 2. 13 i) Nếu f liên tục trên [-L, L] và f(-L)=f(L) và f’ là trơn từng khúc trên [-L, L). Khi đó chuỗi Fourier đầy đủ của hàm f có thể lấy đạo hàm theo từng thành phần và chuỗi kết quả chính là chuỗi Fourier của f’. Chuỗi này hội tụ đến f’ tại nhưng điểm mà f’’ tồn tại.

ĐỊNH LÝ 2. 13 ii) Nếu f liên tục trên [0, L] và f(0)=f(L)=0 và f’ là trơn từng khúc trên [0, L]. Khi đó chuỗi Fourier sine của hàm f có thể lấy đạo hàm theo từng thành phần và chuỗi kết quả chính là chuỗi Fourier cosine của f’. Chuỗi này hội tụ đến f’ tại nhưng điểm mà f’’ tồn tại. iii) Nếu f liên tục trên [0, L] và f’ là trơn từng khúc trên [0, L]. Khi đó chuỗi Fourier cosine của hàm f có thể lấy đạo hàm theo từng thành phần và chuỗi kết quả chính là chuỗi Fourier sine của f’. Chuỗi này hội tụ đến f’ tại nhưng điểm mà f’’ tồn tại.

THỰC HÀNH MATLAB

BÀI TẬP 1 Khai triển Fourier đầy đủ các hàm sau, xác định sự hội tụ trên [ -L; L] và vẽ đồ thị trên [-3 L; 3 L]

BÀI TẬP 2 Khai triển Fourier sine và cosine các hàm sau, xác định sự hội tụ trên [0; L] và vẽ đồ thị trên [-3 L; 3 L]