Nha Trang 2000 Nha Trang Vietnam Aug 14







































- Slides: 42

Nha Trang 2000 Nha Trang, Vietnam, Aug. 14 -18, 2000 SOLUTION OF EIGENVALUE PROBLEM FOR NON-CLASSICALLY DAMPED SYSTEM WITH MULTIPLE EIGENVALUES * In-Won Lee: Professor, KAIST Man-Cheol Kim: Senior Researcher, KRRI Kyu-Hong Shim: Postdoctoral Researcher, KAIST

OUTLINE l PROBLEM DEFINITION l PROPOSED METHOD l NUMERICAL EXAMPLES l CONCLUSIONS Structural Dynamics & Vibration Control Lab. , KAIST, Korea 1

l PROBLEM DEFINITION • Dynamic Equation of Motion (1) where : Mass matrix, Positive definite : Damping matrix : Stiffness matrix, Positive semi-definite : Displacement vector : Load vector Structural Dynamics & Vibration Control Lab. , KAIST, Korea 2

• Methods of Dynamic Analysis • Step by step integration method • Mode superposition method • Mode Superposition Method • Free vibration analysis should be first performed Structural Dynamics & Vibration Control Lab. , KAIST, Korea 3

• Condition of Classical Damping (2) • Example : Rayleigh Damping Structural Dynamics & Vibration Control Lab. , KAIST, Korea 4

• Eigenproblem of classical damping systems (3) where : Real eigenvalue : Natural frequency : Real eigenvector(mode shape) - Low in cost - Straightforward Structural Dynamics & Vibration Control Lab. , KAIST, Korea 5

• Quadratic eigenproblem of non-classically damped systems (4) where : Complex eigenvalue : Complex eigenvector(mode shape) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 6

(5) where : Complex Eigenvalue : Complex Eigenvector (6) - Very expensive An efficient eigensolution technique of non-classically damped systems is required. Structural Dynamics & Vibration Control Lab. , KAIST, Korea 7

• Current Methods for Solving the Non-Classically Damped Eigenproblems • Transformation method: Kaufman (1974) • Perturbation method: Meirovitch et al (1979) • Vector iteration method: Gupta (1974; 1981) • Subspace iteration method: Leung (1995) • Lanczos method: Chen (1993) • Efficient Methods Structural Dynamics & Vibration Control Lab. , KAIST, Korea 8

l PROPOSED METHOD • Find p Smallest Eigenpairs Solve Subject to For and : multiple or close roots If p=1, then distinct root where Structural Dynamics & Vibration Control Lab. , KAIST, Korea 9

• Relations between and Vectors in the Subspace of (7) where (8) (9) • Let subspace of and respect to , then be the vectors in the be orthonormal with (10) (11) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 10

• Introducing Eq. (10) into Eq. (7) (12) • Let where (13) : Symmetric • Then (14) or (15) or (16) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 11

• Multiple or Close Eigenvalues • Multiple eigenvalues case : is a diagonal matrix. Eigenvalues : Eigenvectors : • Close eigenvalues case : is not a diagonal matrix. - Solve the small standard eigenvalue problem. (13) - Get the following eigenpairs. Eigenvalues : Eigenvectors : Structural Dynamics & Vibration Control Lab. , KAIST, Korea (10) 12

• Newton-Raphson Technique (17) (18) (19) where (20) (21) : unknown incremental values Structural Dynamics & Vibration Control Lab. , KAIST, Korea 13

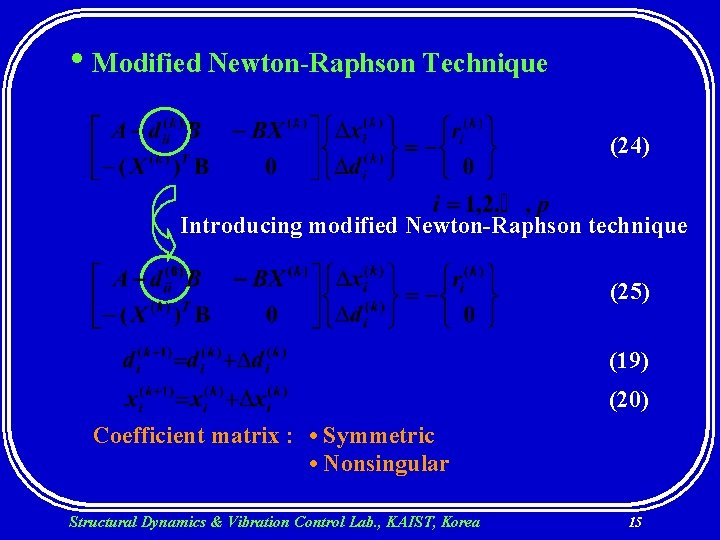
• Introducing Eqs. (19) and (20) into Eqs. (17) and (18) and neglecting nonlinear terms (22) (23) where : residual vector • Matrix form of Eqs. (22) and (23) (24) Coefficient matrix : • Symmetric • Nonsingular Structural Dynamics & Vibration Control Lab. , KAIST, Korea 14

• Modified Newton-Raphson Technique (24) Introducing modified Newton-Raphson technique (25) (19) (20) Coefficient matrix : • Symmetric • Nonsingular Structural Dynamics & Vibration Control Lab. , KAIST, Korea 15

• Algorithm of Proposed Method • Step 1: Start with approximate eigenpairs • Step 2: Solve for and • Step 3: Compute Structural Dynamics & Vibration Control Lab. , KAIST, Korea 16

• Step 4: Check the error norm. Error norm = n If the error norm is more than the tolerance, then go to Step 2 and if not, go to Step 5. • Step 5: Check if is a diagonal matrix, go to Step 6, if not, go to Step 7. Structural Dynamics & Vibration Control Lab. , KAIST, Korea 17

• Step 6: Multiple case • Step 7: Close case • Go to step 8. • Step 8: Check the error norm. Error norm = • Stop ! Structural Dynamics & Vibration Control Lab. , KAIST, Korea 18

• Initial Values of the Proposed Method • Intermediate results of the iteration methods - Vector iteration method - Subspace iteration method • Results of the approximate methods - Static Condensation method - Lanczos method Structural Dynamics & Vibration Control Lab. , KAIST, Korea 19

l NUMERICAL EXAMPLES • Structures • Cantilever beam(distinct) • Grid structure(multiple) • Three-dimensional framed structure(close) • Analysis Methods • Proposed method • Subspace iteration method (Leung 1988) • Lanczos method (Chen 1993) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 20

• Comparisons • Solution time(CPU) • Convergence • Convex with 100 MIPS, 200 MFLOPS Structural Dynamics & Vibration Control Lab. , KAIST, Korea 21

Cantilever Beam with Lumped Dampers (Distinct Case) Material Properties 1 2 3 4 5 Tangential Damper : c = 0. 3 Rayleigh Damping : = = 0. 001 Young’s Modulus : 1000 99 100 101 Mass Density : 1 C Cross-section Inertia : 1 Cross-section Area : 1 System Data Number of Equations : 200 Number of Matrix Elements : 696 Maximum Half Bandwidths : 4 Mean Half Bandwidths : 4 Structural Dynamics & Vibration Control Lab. , KAIST, Korea 22

• Results of Cantilever Beam Structure (Distinct) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 23

• CPU Time for 10 Lowest Eigenpairs, Cantilever Beam Structural Dynamics & Vibration Control Lab. , KAIST, Korea 24

Starting values of proposed method : 1 st, 2 nd eigenpairs : 3 rd, 4 th eigenpairs : 5 th, 6 th eigenpairs : 7 th, 8 th eigenpairs : 9 th, 10 th eigenpairs Convergence by Lanczos method(Chen 1993) Cantilever beam (distinct) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 25

: Proposed Method : Subspace Iteration Method (q=2 p) Convergence of the 1 st eigenpair Cantilever beam (distinct) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 26

: Proposed Method : Subspace Iteration Method (q=2 p) Convergence of the 5 th eigenpair Cantilever beam (distinct) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 27

Grid Structure with Lumped Dampers (Multiple Case) Material Properties Tangential Damper : c = 0. 3 100@0. 1=10 Rayleigh Damping : = = 0. 001 Young’s Modulus : 1, 000 Mass Density : 1 Cross-section Inertia : 1 Cross-section Area : 1 System Data Number of Equations : 590 Number of Matrix Elements : 8, 115 Maximum Half Bandwidths : 15 100@0. 1=10 Mean Half Bandwidths : 14 Structural Dynamics & Vibration Control Lab. , KAIST, Korea 28

• Results of Grid Structure (Multiple) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 29

• CPU Time for 10 Lowest Eigenpairs, Grid Structure Structural Dynamics & Vibration Control Lab. , KAIST, Korea 30

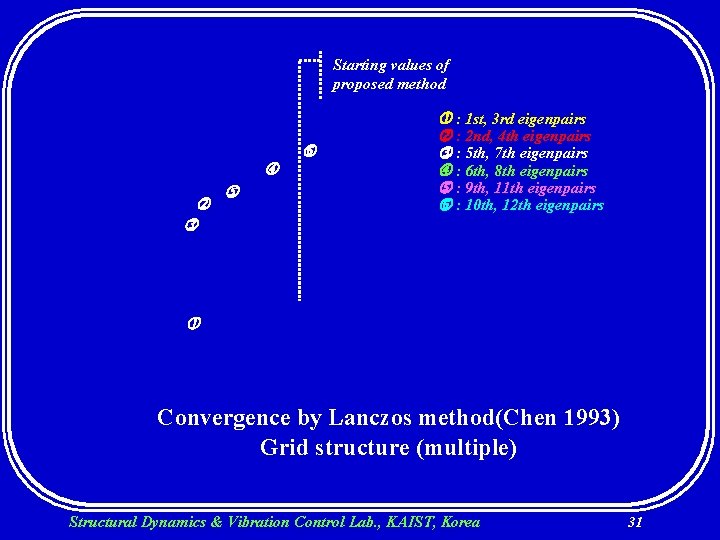
Starting values of proposed method : 1 st, 3 rd eigenpairs : 2 nd, 4 th eigenpairs : 5 th, 7 th eigenpairs : 6 th, 8 th eigenpairs : 9 th, 11 th eigenpairs : 10 th, 12 th eigenpairs Convergence by Lanczos method(Chen 1993) Grid structure (multiple) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 31

: Proposed Method : Subspace Iteration Method (q=2 p) Convergence of the 2 nd eigenpair Grid structure (multiple) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 32

: Proposed Method : Subspace Iteration Method (q=2 p) Convergence of the 9 th eigenpair Grid structure (multiple) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 33

Three-Dimensional Framed Structure with Lumped Dampers(Close Case) 2@3. 01=6. 02 2@3=6 6@3. 01=18. 06 6@3=18 12@3=36 Structural Dynamics & Vibration Control Lab. , KAIST, Korea 34

Material Properties Lumped Damper : c = 12, 000. 0 Rayleigh Damping : =-0. 1755 = 0. 02005 Young’s Modulus : 2. 1 E+11 Mass Density : 7, 850 Cross-section Inertia : 8. 3 E-06 Cross-section Area : 0. 01 System Data Number of Equations : 1, 128 Number of Matrix Elements : 135, 276 Maximum Half Bandwidths : 300 Mean Half Bandwidths : 120 Structural Dynamics & Vibration Control Lab. , KAIST, Korea 35

• Results of Three-Dimensional Frame Structure (Close) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 36

• CPU Time for 12 Lowest Eigenpairs, 3 -D. Frame Structural Dynamics & Vibration Control Lab. , KAIST, Korea 37

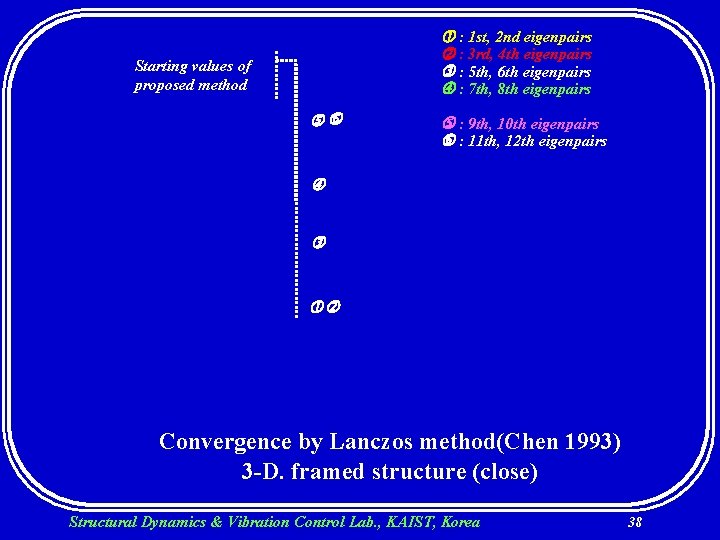
: 1 st, 2 nd eigenpairs : 3 rd, 4 th eigenpairs : 5 th, 6 th eigenpairs : 7 th, 8 th eigenpairs Starting values of proposed method : 9 th, 10 th eigenpairs : 11 th, 12 th eigenpairs Convergence by Lanczos method(Chen 1993) 3 -D. framed structure (close) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 38

: Proposed Method : Subspace Iteration Method (q=2 p) Convergence of the 9 th eigenpair 3 -D. framed structure (close) Structural Dynamics & Vibration Control Lab. , KAIST, Korea 39

l CONCLUSIONS • The proposed method • is simple • guarantees numerical stability • converges fast. An efficient Eigensolution technique ! Structural Dynamics & Vibration Control Lab. , KAIST, Korea 40

Thank you for your attention. Structural Dynamics & Vibration Control Lab. , KAIST, Korea 41
 Dừng chân nghỉ lại nha trang
Dừng chân nghỉ lại nha trang Marso 29 1891
Marso 29 1891 Words with root words
Words with root words Aug q
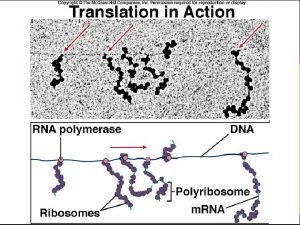
Aug q Aug methionine start codon
Aug methionine start codon Aug comm device
Aug comm device Amino acids table
Amino acids table Translasjon
Translasjon Muôn thiên thần cánh trắng
Muôn thiên thần cánh trắng Tình yêu thiên chúa như trăng như sao
Tình yêu thiên chúa như trăng như sao Bọn em hai đứa cùng tên
Bọn em hai đứa cùng tên Tập thơ vầng trăng quầng lửa
Tập thơ vầng trăng quầng lửa Uyen trang nguyen
Uyen trang nguyen Lóa màu trắng hoa
Lóa màu trắng hoa Trang ngy
Trang ngy Vẽ trang trí chậu cảnh lớp 8
Vẽ trang trí chậu cảnh lớp 8 Dr trang ha
Dr trang ha Mối quan hệ giữa gen và tính trạng
Mối quan hệ giữa gen và tính trạng Nhà văn o'hen ri
Nhà văn o'hen ri Vẽ trang trí đồ vật có dạng hình chữ nhật
Vẽ trang trí đồ vật có dạng hình chữ nhật Tạo đặc điểm và thiết kế trang phục rối
Tạo đặc điểm và thiết kế trang phục rối Prince of songkla university trang campus
Prince of songkla university trang campus Hàm trạng thái
Hàm trạng thái Các trạng thái của tiến trình
Các trạng thái của tiến trình Gấu trắng
Gấu trắng Dr thu-trang phung
Dr thu-trang phung Con bướm trắng lượn cành hồng
Con bướm trắng lượn cành hồng Trang tr
Trang tr Vẽ cổng trại
Vẽ cổng trại Trang tnh
Trang tnh Vẽ và trang trí lọ hoa
Vẽ và trang trí lọ hoa để nguyên nước chấm cổ truyền
để nguyên nước chấm cổ truyền Các bước trang trí hình vuông
Các bước trang trí hình vuông Bài tập về nhà
Bài tập về nhà Fcclainc.org logo
Fcclainc.org logo Tôi vui mừng tiến bước về nhà cha
Tôi vui mừng tiến bước về nhà cha Chuỗi cung ứng th true milk
Chuỗi cung ứng th true milk Bớt đầu thì bé nhất nhà
Bớt đầu thì bé nhất nhà Nhà máy thủy điện thác bà
Nhà máy thủy điện thác bà Một nhà thơ chân chính
Một nhà thơ chân chính Bài tập về nhà
Bài tập về nhà Nhà hình xoắn ở dưới ao
Nhà hình xoắn ở dưới ao Nhà tôi ở hà nội cách hồ gươm không xa
Nhà tôi ở hà nội cách hồ gươm không xa