NFAs With Transitions Definition and examples Transition table

NFA’s With ε-Transitions • • • Definition and examples Transition table and ECLOSS Definition of delta-hat and string testing Given e-NFA find equivalent NFA Given e-NFA find equivalent DFA 1

Definition of ε-Transitions • ε-Transitions: Spontaneous transitions between states. • Occur on the empty string, e, at any point in the processing of the input string • Another way to let NFA be in more than one state at the same time. 2

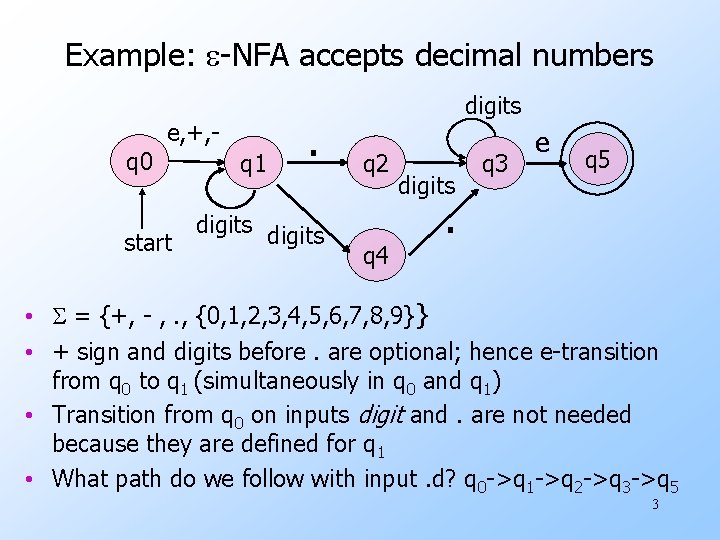
Example: e-NFA accepts decimal numbers e, +, q 0 start q 1 . digits q 2 q 4 digits q 3 e q 5 . • S = {+, - , . , {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}} • + sign and digits before. are optional; hence e-transition from q 0 to q 1 (simultaneously in q 0 and q 1) • Transition from q 0 on inputs digit and. are not needed because they are defined for q 1 • What path do we follow with input. d? q 0 ->q 1 ->q 2 ->q 3 ->q 5 3

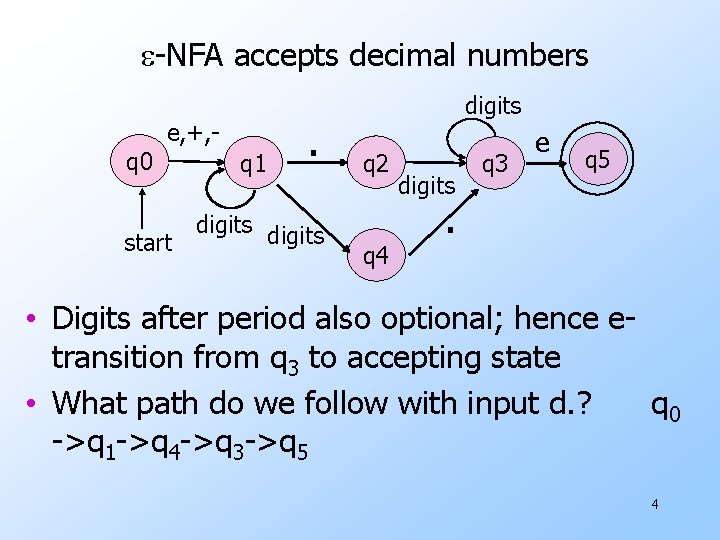
e-NFA accepts decimal numbers e, +, q 0 start q 1 . digits q 2 q 4 digits q 3 e q 5 . • Digits after period also optional; hence etransition from q 3 to accepting state • What path do we follow with input d. ? q 0 ->q 1 ->q 4 ->q 3 ->q 5 4

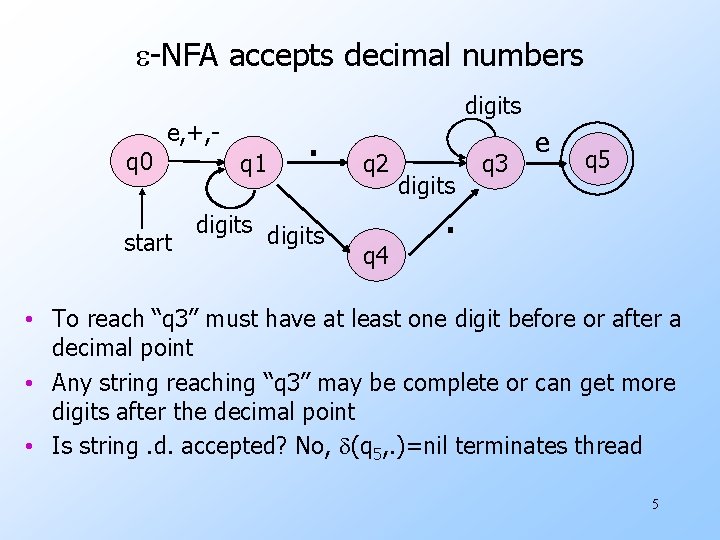
e-NFA accepts decimal numbers e, +, q 0 start q 1 . digits q 2 q 4 digits q 3 e q 5 . • To reach “q 3” must have at least one digit before or after a decimal point • Any string reaching “q 3” may be complete or can get more digits after the decimal point • Is string. d. accepted? No, d(q 5, . )=nil terminates thread 5

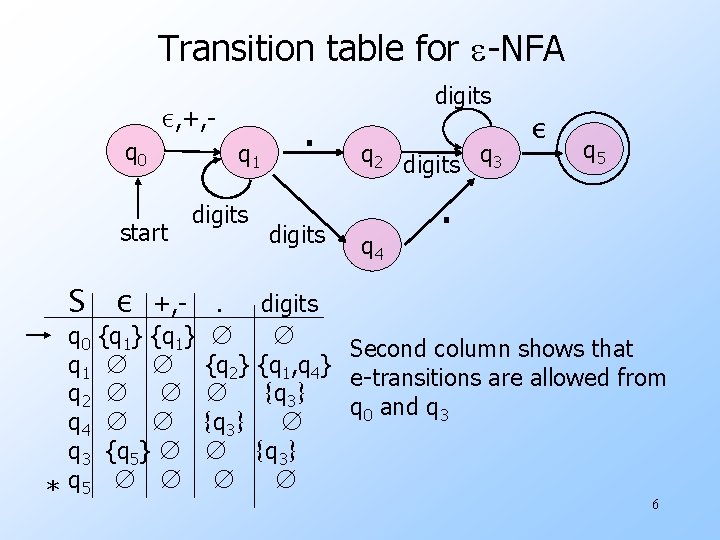
Transition table for e-NFA q 0 ε, +, - start S ε q 0 q 1 q 2 q 4 q 3 * q 5 q 1 digits +, {q 1} ∅ ∅ ∅ {q 5} ∅ ∅ ∅ . ∅ {q 2} ∅ {q 3} ∅ ∅ . digits q 2 digits q 3 q 4 ε q 5 . digits ∅ Second column shows that {q 1, q 4} e-transitions are allowed from {q 3} q 0 and q 3 ∅ {q 3} ∅ 6

e-Closure of states Both ECLOSE(q) (used in text) and CL(q) (used on slides) denote the set of states {q, all states reached from q by εtransitions, both directly and indirectly} e-closure of a set of states = union of the e-closures of each state. e-closure of the empty set = empty set CL(nil) = nil 7

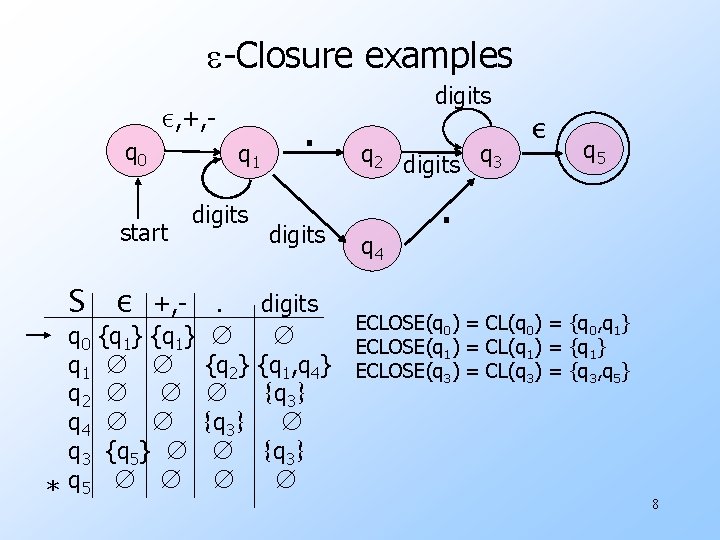
e-Closure examples q 0 ε, +, - start S ε q 0 q 1 q 2 q 4 q 3 * q 5 q 1 digits +, {q 1} ∅ ∅ ∅ {q 5} ∅ ∅ ∅ . ∅ {q 2} ∅ {q 3} ∅ ∅ . digits ∅ {q 1, q 4} {q 3} ∅ digits q 2 digits q 3 q 4 ε q 5 . ECLOSE(q 0) = CL(q 0) = {q 0, q 1} ECLOSE(q 1) = CL(q 1) = {q 1} ECLOSE(q 3) = CL(q 3) = {q 3, q 5} 8

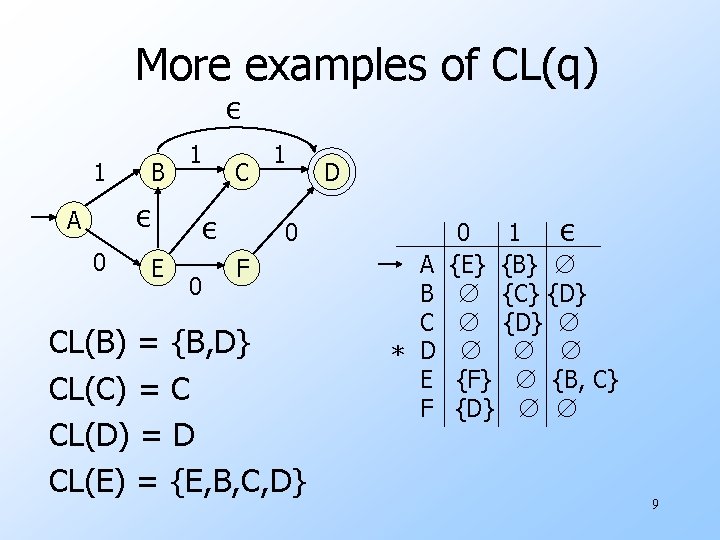
More examples of CL(q) ε 1 B ε A 0 E 1 C ε 0 1 D 0 F CL(B) = {B, D} CL(C) = C CL(D) = D CL(E) = {E, B, C, D} A B C * D E F 0 1 ε {E} {B} ∅ ∅ {C} {D} ∅ ∅ ∅ ∅ {F} ∅ {B, C} {D} ∅ ∅ 9

Using CL(q) to define d˄ (q, w) when e-transitions may be present. Basis: d˄ (q, ε) = CL(q) d˄ (q, a) = CL(d(q, a)) Induction: Let w=xa and (q, x)={p 1, …pk} be all and only the states reached from q in the processing of string x, including states reached by etransitions. d˄ (q, w) = CL(d˄ (q, xa)) = CL(d(d˄ (q, x), a)) = CL(d({p 1…pk}, a)) = CL({d(p 1, a), …, d(pk, a)}) = CL(d(p 1, a))UCL(d(p 2, a))U…UCL(d(pk, a)) Each CL(d(pi, a)) in string unions can be evaluated from the transition table ˄(q, w). of the e-NFA, resulting in a set of states that is d ˄ (q 0, w) contains an accepting state. L(ε-NFA) = set of strings w such that d 10

Is string 011 accepted by e-NFA below? Use the method of all prefixes with ECLOSS on all states 0 1 ε A {E} {B} ∅ B ∅ {C} {D} C ∅ {D} ∅ *D ∅ ∅ ∅ E {F} ∅ {B, C} ˄d(A, ε) = CL(A) = {A} F {D} ∅ ∅ ˄d(A, 0) = CL(E) = {E, B, C, D} d˄(A, 01)=CL(∅UCUDU∅U)=CL({C, D})=CL(C)UCL(D)={C, D} d˄ (A, 011) = CL(DU∅)=CL(D)={D} accepted Are strings 0110 and 0111 Accepted? No, d˄ (A, 0110) = CL(d(D, 0)) = CL(nil) = nil terminates thread Similarly for 0111. 11

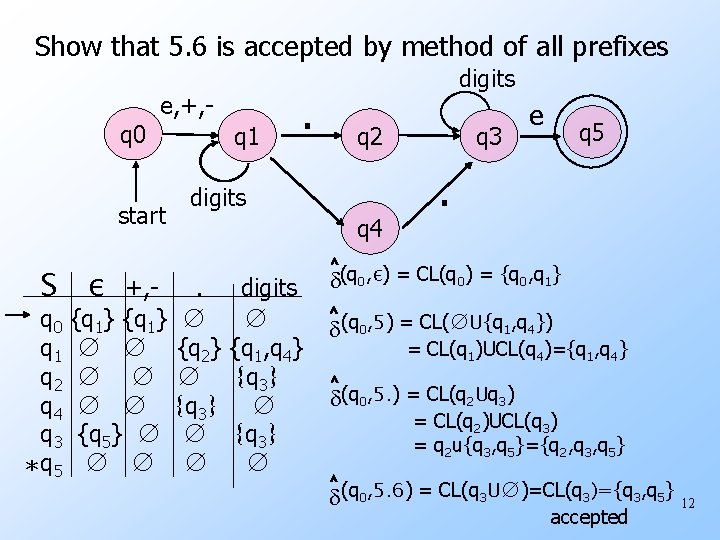
Show that 5. 6 is accepted by method of all prefixes e, +, q 0 start S ε q 0 q 1 q 2 q 4 q 3 * q 5 +, {q 1} ∅ ∅ ∅ {q 5} ∅ ∅ ∅ q 1 . digits q 2 digits q 4. ∅ {q 2} ∅ {q 3} ∅ ∅ digits ∅ {q 1, q 4} {q 3} ∅ q 3 e q 5 . d˄(q 0, ε) = CL(q 0) = {q 0, q 1} d˄ (q 0, 5) = CL(∅U{q 1, q 4}) = CL(q 1)UCL(q 4)={q 1, q 4} d˄ (q 0, 5. ) = CL(q 2 Uq 3) = CL(q 2)UCL(q 3) = q 2 u{q 3, q 5}={q 2, q 3, q 5} d˄ (q 0, 5. 6) = CL(q 3 U∅)=CL(q 3)={q 3, q 5} 12 accepted

Given e-NFA find the equivalent NFA • Given an ε-NFA that has states QE, alphabet ΣE, start state q 0 E, final states FE, and transition function δE. Construct NFA with • ΣN= ΣE, QN=QE and q 0 N = CL(q 0 E) • For ever state q in QE, compute δN(q, a) from δE(q, a) as follows: • Let S = CL(q). • δN(q, a) is the union over all p in S of δE(p, a) • FN = the set of states q such that CL(q) contains a state of FE. 13

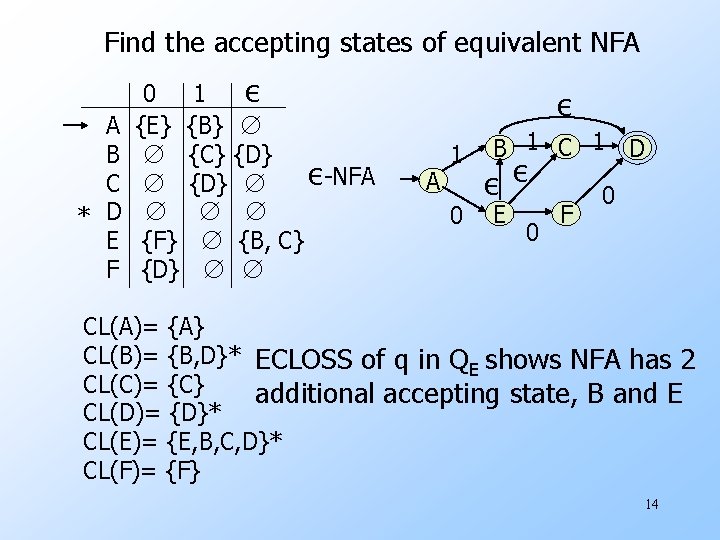
Find the accepting states of equivalent NFA A B C * D E F 0 1 ε {E} {B} ∅ ∅ {C} {D} ε-NFA ∅ {D} ∅ ∅ {F} ∅ {B, C} {D} ∅ ∅ ε A 1 0 B 1 C 1 D εε E 0 F 0 CL(A)= {A} CL(B)= {B, D}* ECLOSS of q in Q shows NFA has 2 E CL(C)= {C} additional accepting state, B and E CL(D)= {D}* CL(E)= {E, B, C, D}* CL(F)= {F} 14

Construct the transition table of equivalent NFA ε-NFA A B C * D E F 0 1 ε {E} {B} ∅ ∅ {C} {D} ∅ ∅ ∅ ∅ {F} ∅ {B, C} {D} ∅ ∅ Let S = CL(q). δN(q, a) is the union over all p in S of δE(p, a) CL(A) = {A} d. N(A, 0)=d. E(A, 0)={E}, d. N(A, 1)=d. E(A, 1)={B} CL(B) = {B, D} d. N(B, 0)=d. E(B, 0) U d. E(D, 0)=nil U nil = nil d. N(B, 1)=d. E(B, 1) U d. E(D, 1)={C} U nil = {C} CL(C) = {C} d. N(C, 0)=d. E(C, 0)=nil, d. N(C, 1)=d. E(C, 1)={D} CL(D) = {D} d. N(D, 0)=d. E(D, 0)=nil, d. N(D, 1)=d. E(D, 1)=nil 15

More construct the transition table of equivalent NFA A B C * D E F 0 1 ε {E} {B} ∅ ∅ {C} {D} ∅ ∅ ∅ ∅ {F} ∅ {B, C} {D} ∅ ∅ ε-NFA Let S = CL(q). δN(q, a) is the union over all p in S of δE(p, a) CL(E) = {E, B, C, D} d. N(E, 0)=d. E(E, 0) U d. E(B, 0) U d. E(C, 0) U d. E(D, 0)={F} U nil={F} d. N(E, 1)=d. E(E, 1) U d. E(B, 1) U d. E(C, 1) U d. E(D, 1)=nil U {C} U {D} U nil={C, D} CL(F) = {F} d. N(F, 0) = d. E(F, 0) ={D}, dn(F, 1) = d. E(F, 1) = nil 16

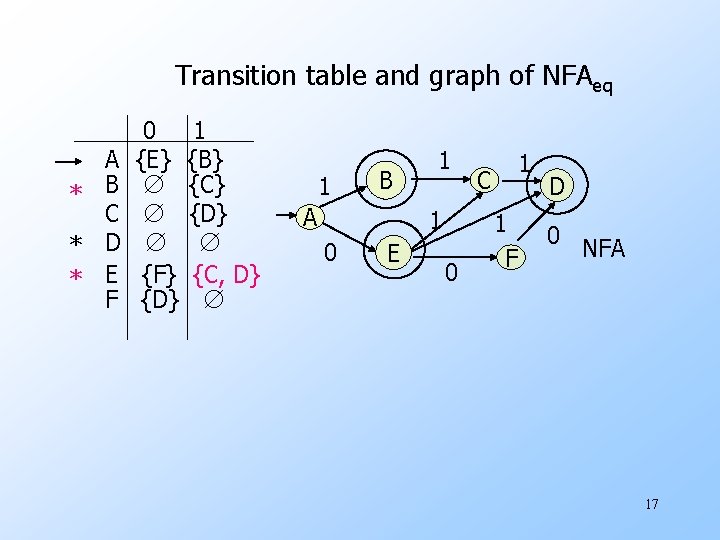
Transition table and graph of NFAeq A * B C * D * E F 0 1 {E} {B} ∅ {C} ∅ {D} ∅ ∅ {F} {C, D} {D} ∅ 1 B A 1 1 0 E 0 1 C 1 F D 0 NFA 17

Cpt. S 317 Fall 2020 Assignment 4 For the e-NFA defined by the transition table below: 1. Find the ECLOSE of each state 2. Test the acceptance of string bab by the e-NFA using the method of all prefixes. 3. Derive the transition function table of the equivalent NFA (show your algebra). 4. Test the acceptance of string bab by NFAeq using the method of all prefixes e a b c ->p nil p q r q p q r nil *r p r nil p 18

Given e-NFA find equivalent DFA Add ECLOSS to lazy subset construction start state of DFA is CL(q 0 E), where q 0 E is start state of e-NFA “lazy” subset construction of DFA from e-NFA same as for DFA from NFA except that we use the ECLOSS of the states in the transition table of e-NFA 19

Lazy sublet construction of the equivalent DFA A B C D * E F • • • 0 1 ε {E} {B} ∅ ∅ {C} {D} ∅ ∅ ∅ ∅ {F} ∅ {B, C} {D} ∅ ∅ ε-NFA CL(A)= {A} CL(B)= {B, D} CL(C)= {C} CL(D)= {D} CL(E)= {E, B, C, D} CL(F)= {F} Since CL(A)={A}, {A} is the start state DFAeq Use transition table of e-NFA with ECLOSS of states to find where {A} goes under 0 and 1. d. D(A, 0)=CL(E)={E, B, C, D} d. D(A, 1)=CL(B)={B, D} {E, B, C, D} and {B, D} are states of DFAeq Find where they go under 0 and 1 20 Continue until no new subset are encountered

Lazy sublet construction of the equivalent DFA A B C D * E F 0 1 ε {E} {B} ∅ ∅ {C} {D} ∅ ∅ ∅ ∅ {F} ∅ {B, C} {D} ∅ d. E(E, 0) ε-NFA CL(A)= {A} CL(B)= {B, D} CL(C)= {C} CL(D)= {D} CL(E)= {E, B, C, D} CL(F)= {F} {E, B, C, D} is a state of DFAeq Find where it go under 0 and 1 d. D({E, B, C, D}, 0)=CL(d. E(E, 0)Ud. E(B, 0)Ud. E(C, 0)Ud. E(D, 0)) CL(FU∅U∅U∅)=CL(F)=F d. D({E, B, C, D}, 1)=CL(d. E(E, 1)Ud. E(B, 1)Ud. E(C, 1)Ud. E(D, 1)) CL(∅UCu. DU∅)=CL({C, D})=CL(C)UCL(D)={C, D} 21

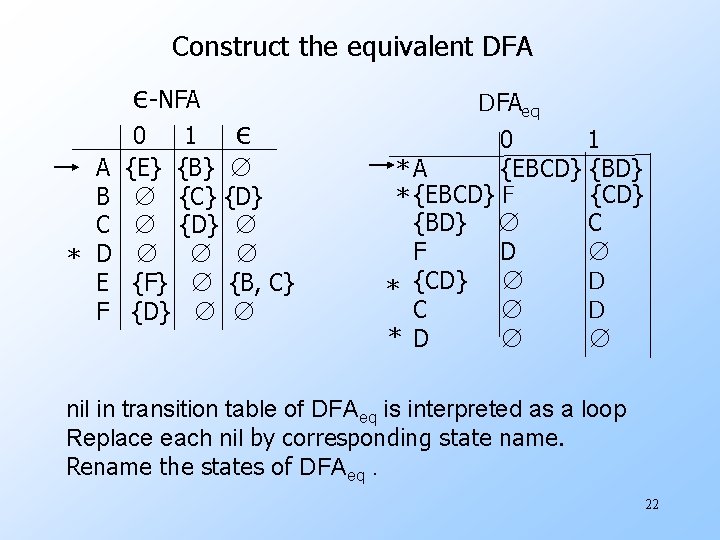
Construct the equivalent DFA ε-NFA A B C * D E F 0 1 ε {E} {B} ∅ ∅ {C} {D} ∅ ∅ ∅ ∅ {F} ∅ {B, C} {D} ∅ ∅ DFAeq 0 1 {EBCD} {BD} *A {CD} * {EBCD} F {BD} ∅ C F D ∅ D * {CD} ∅ C ∅ D * D ∅ ∅ nil in transition table of DFAeq is interpreted as a loop Replace each nil by corresponding state name. Rename the states of DFAeq. 22

Rename the states in DFAeq 0 1 A {BCDE} {BD} {CD} * {BCDE} F C * {BD} F D F * {CD} D C C D D D *D * * q 0 q 1 q 2 q 3 q 4 q 5 q 6 0 q 1 q 3 q 2 q 6 q 4 q 5 q 6 1 q 2 q 4 q 5 q 3 q 6 q 6 e-NFA accepts string 011. Use the delta-hat to show that DFAeq accepts string 011. 23

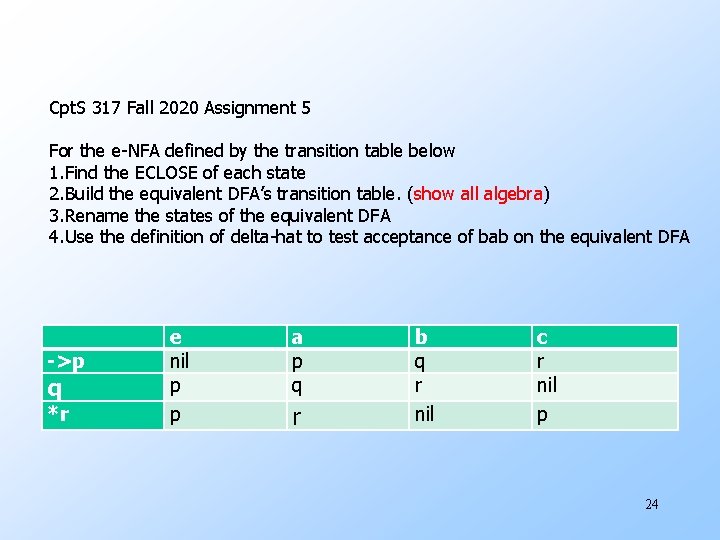
Cpt. S 317 Fall 2020 Assignment 5 For the e-NFA defined by the transition table below 1. Find the ECLOSE of each state 2. Build the equivalent DFA’s transition table. (show all algebra) 3. Rename the states of the equivalent DFA 4. Use the definition of delta-hat to test acceptance of bab on the equivalent DFA ->p q *r e nil p p a p q r b q r nil c r nil p 24