NFAs accept the Regular Languages 1 Equivalence of

NFAs accept the Regular Languages 1

Equivalence of Machines Definition: Machine is equivalent to machine if 2

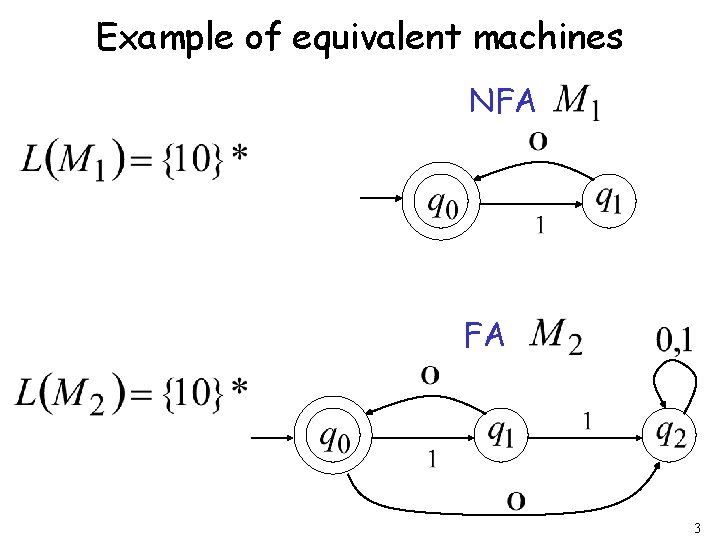
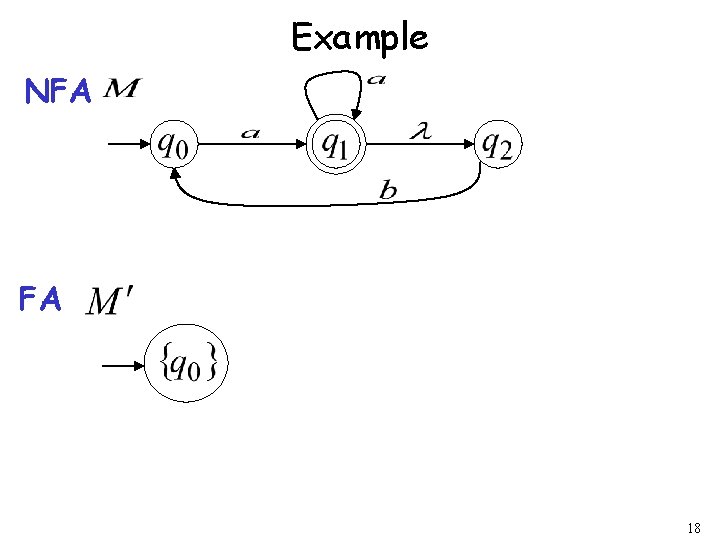
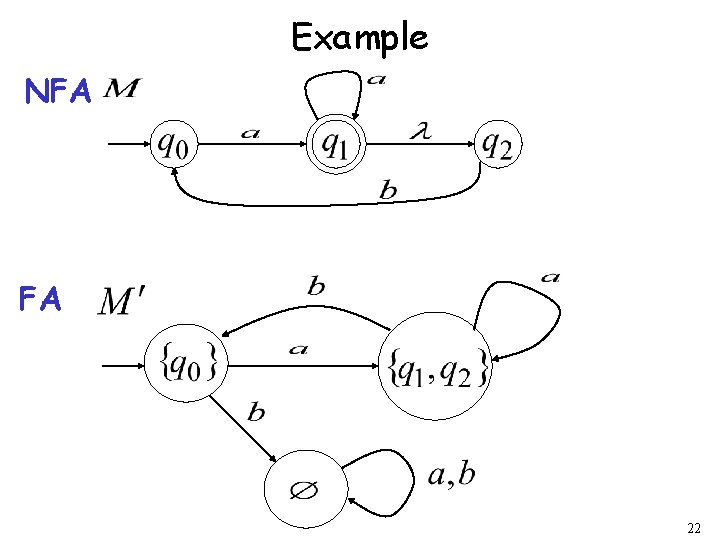
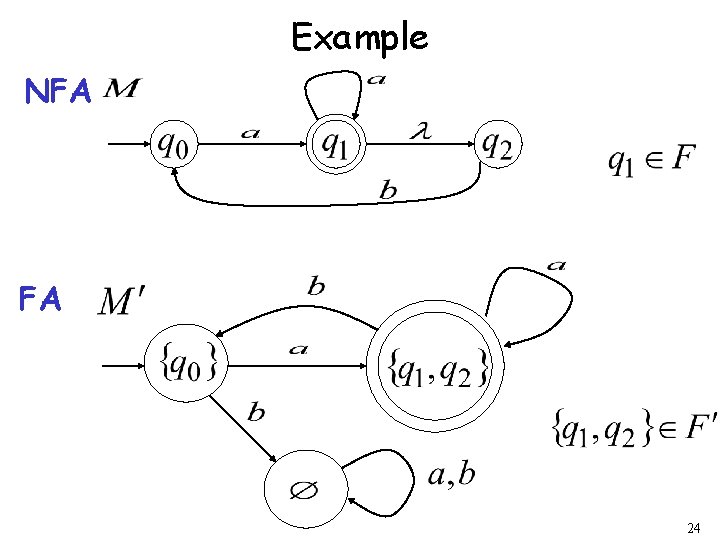
Example of equivalent machines NFA FA 3

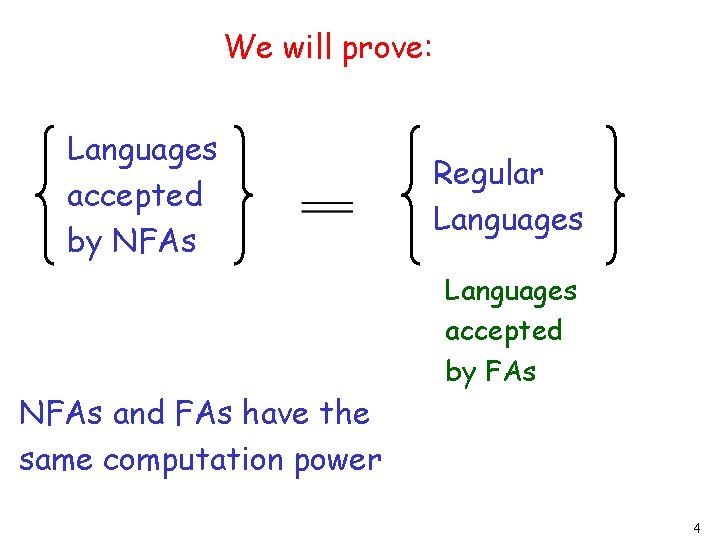
We will prove: Languages accepted by NFAs and FAs have the same computation power Regular Languages accepted by FAs 4

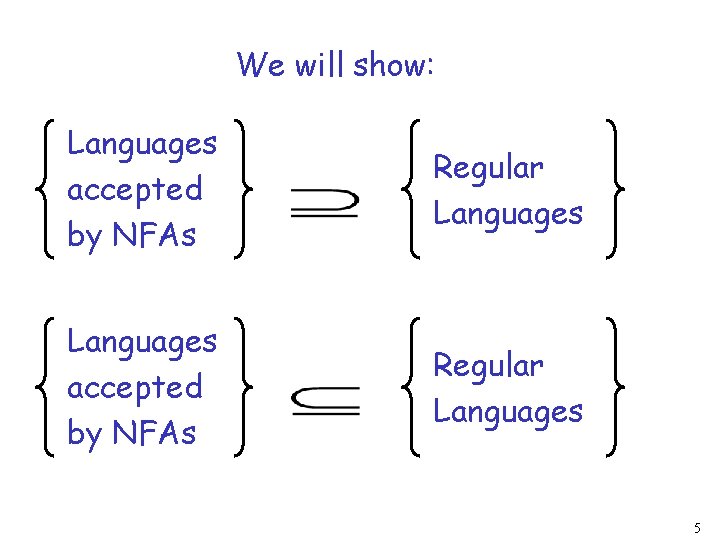
We will show: Languages accepted by NFAs Regular Languages 5

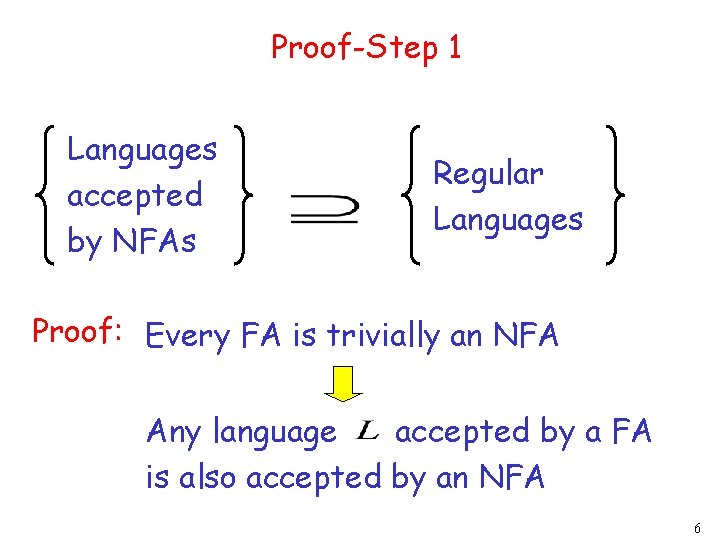
Proof-Step 1 Languages accepted by NFAs Regular Languages Proof: Every FA is trivially an NFA Any language accepted by a FA is also accepted by an NFA 6

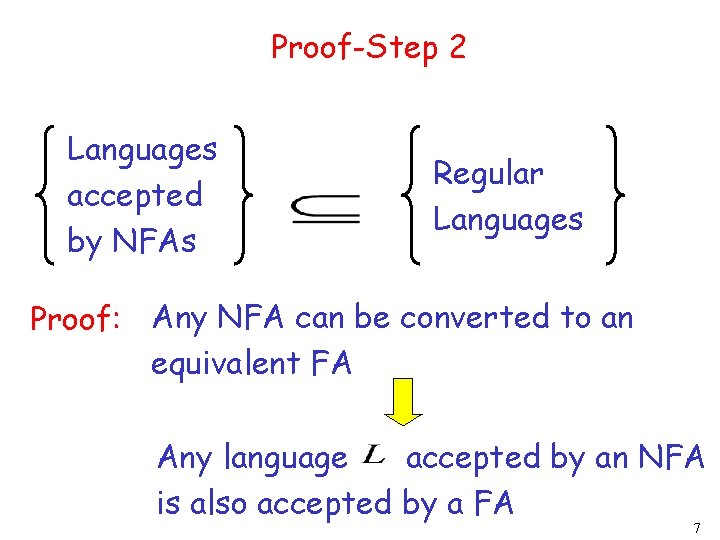
Proof-Step 2 Languages accepted by NFAs Regular Languages Proof: Any NFA can be converted to an equivalent FA Any language accepted by an NFA is also accepted by a FA 7

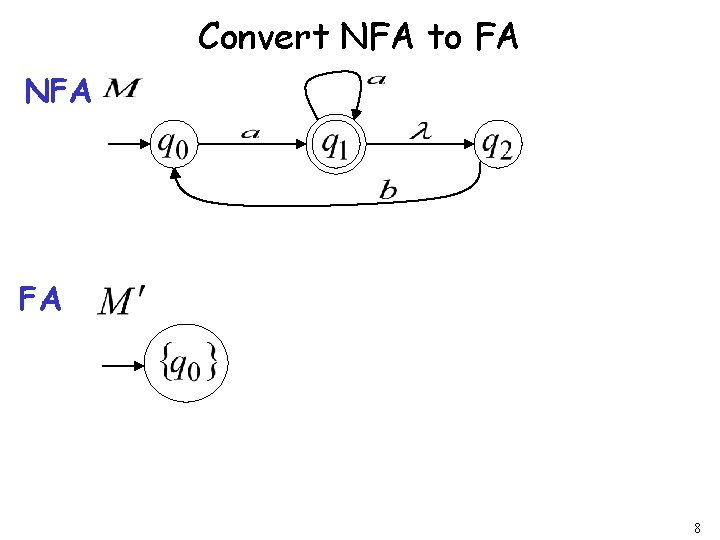
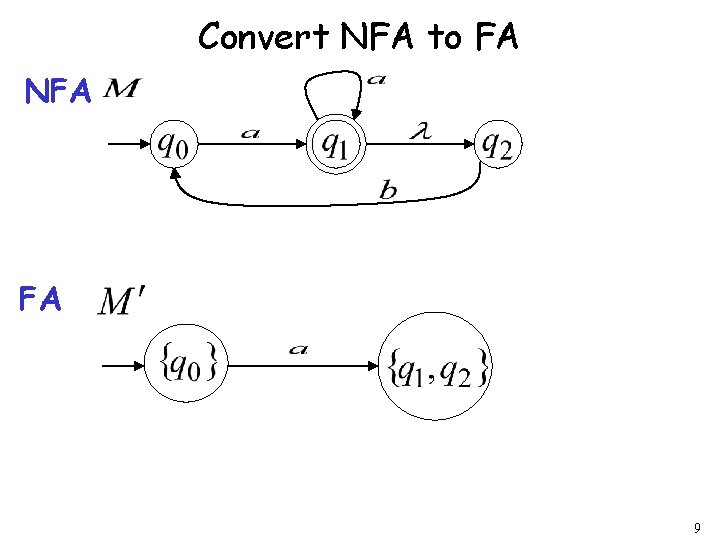
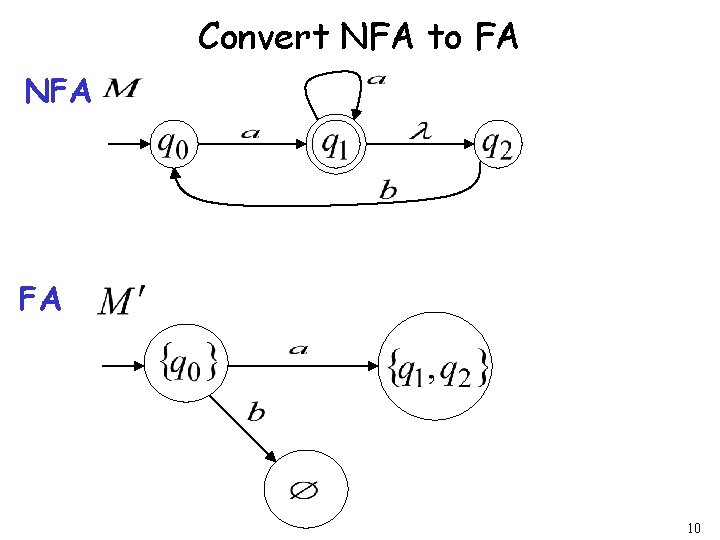
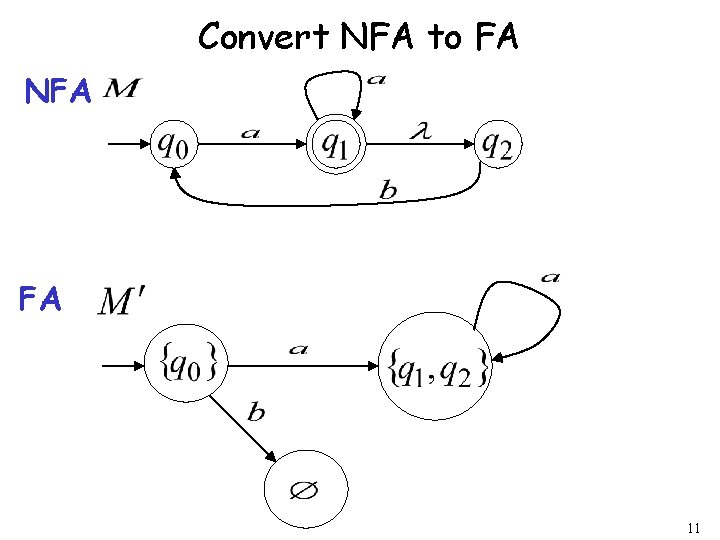
Convert NFA to FA NFA FA 8

Convert NFA to FA NFA FA 9

Convert NFA to FA NFA FA 10

Convert NFA to FA NFA FA 11

Convert NFA to FA NFA FA 12

Convert NFA to FA NFA FA 13

Convert NFA to FA NFA FA 14

NFA to FA: Remarks We are given an NFA We want to convert it to an equivalent FA With 15

If the NFA has states the FA has states in the powerset 16

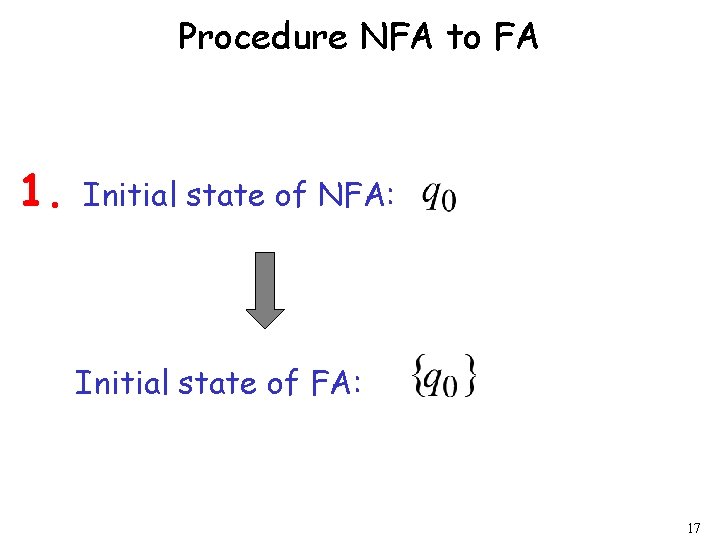
Procedure NFA to FA 1. Initial state of NFA: Initial state of FA: 17

Example NFA FA 18

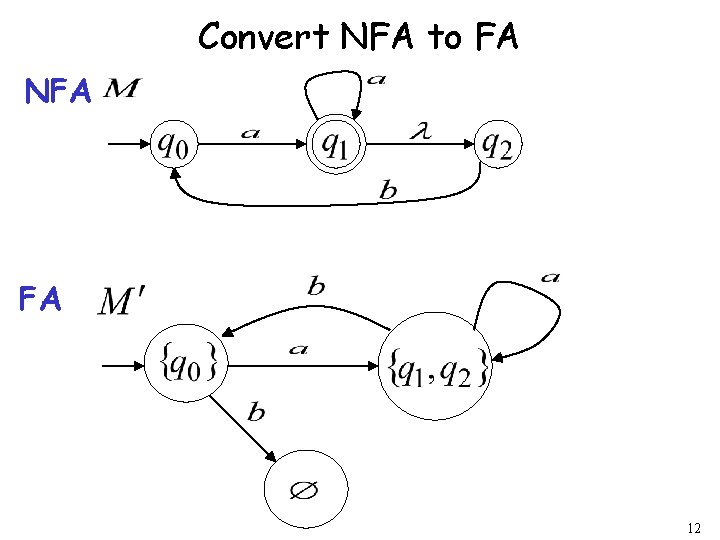
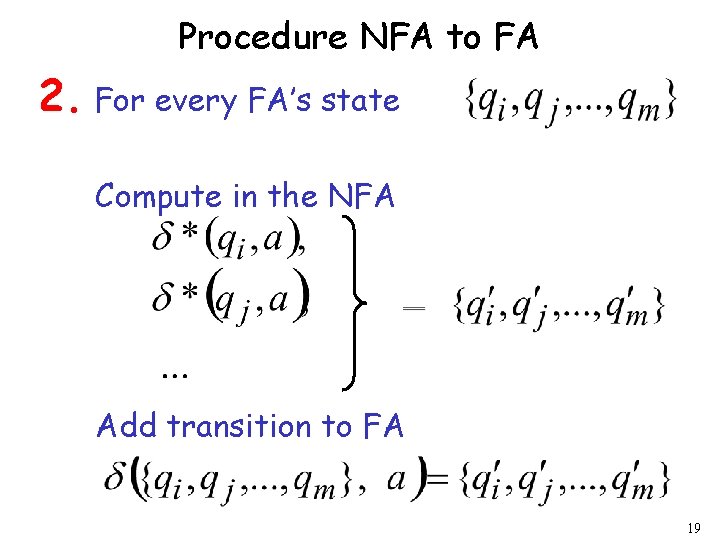
Procedure NFA to FA 2. For every FA’s state Compute in the NFA Add transition to FA 19

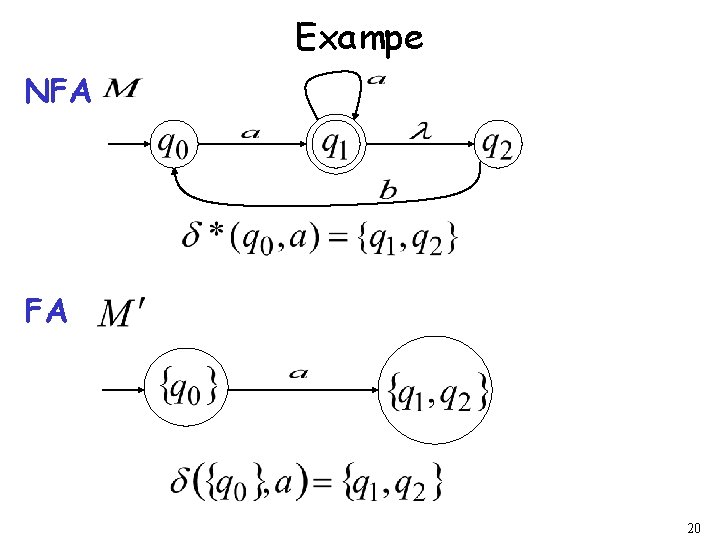
Exampe NFA FA 20

Procedure NFA to FA Repeat Step 2 for all letters in alphabet, until no more transitions can be added. 21

Example NFA FA 22

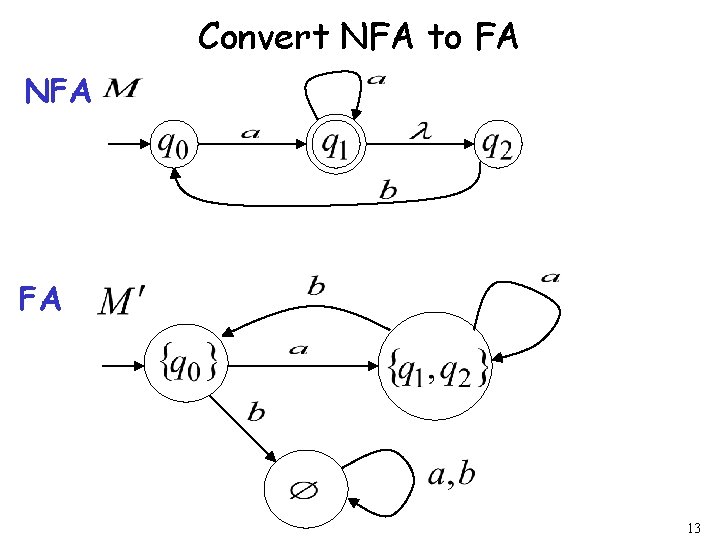
Procedure NFA to FA 3. For any FA state If is accepting state in NFA Then, is accepting state in FA 23

Example NFA FA 24

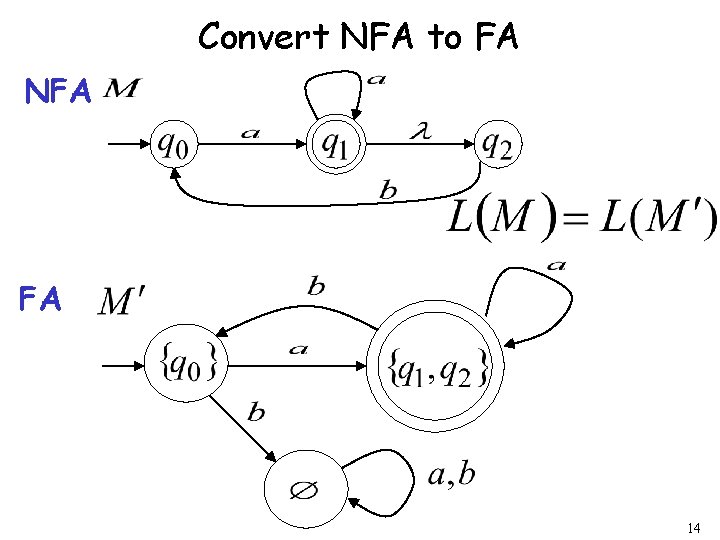
Theorem Take NFA Apply procedure to obtain FA Then and are equivalent : 25

Proof AND 26

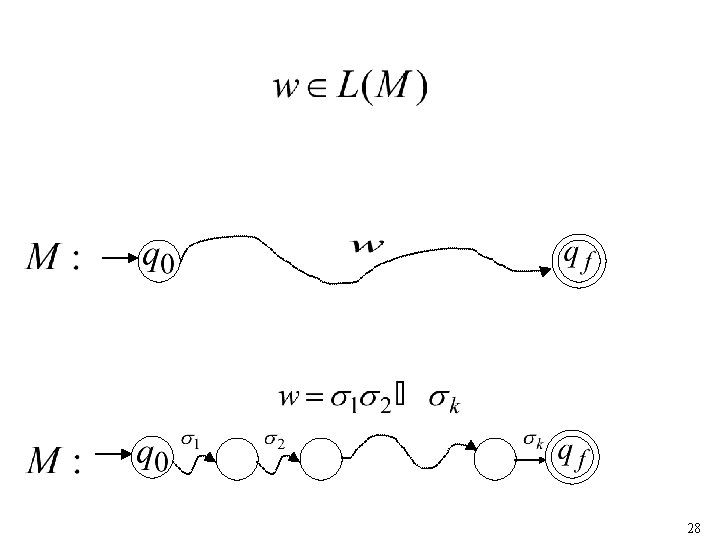
First we show: Take arbitrary: We will prove: 27

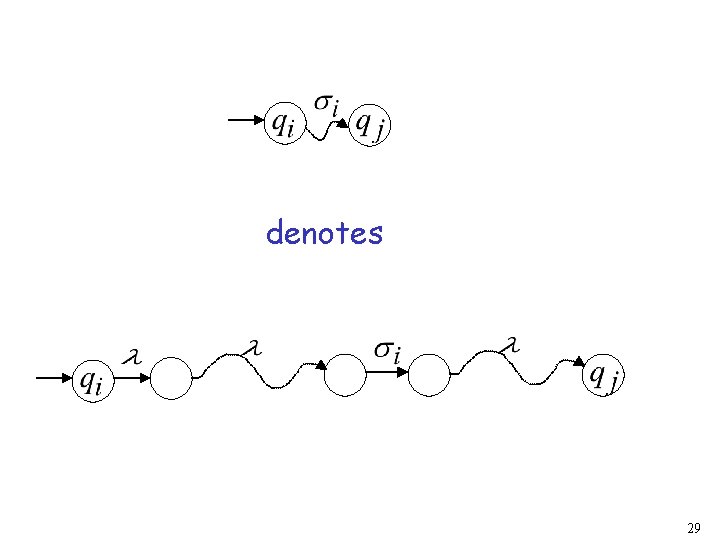
28

denotes 29

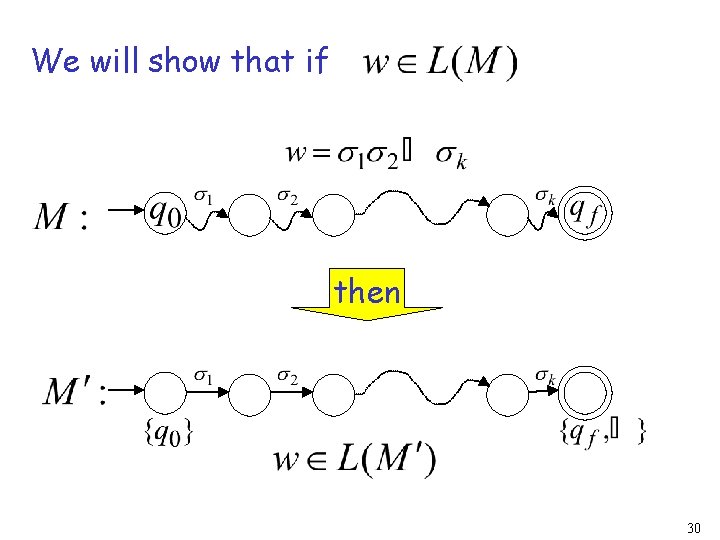
We will show that if then 30

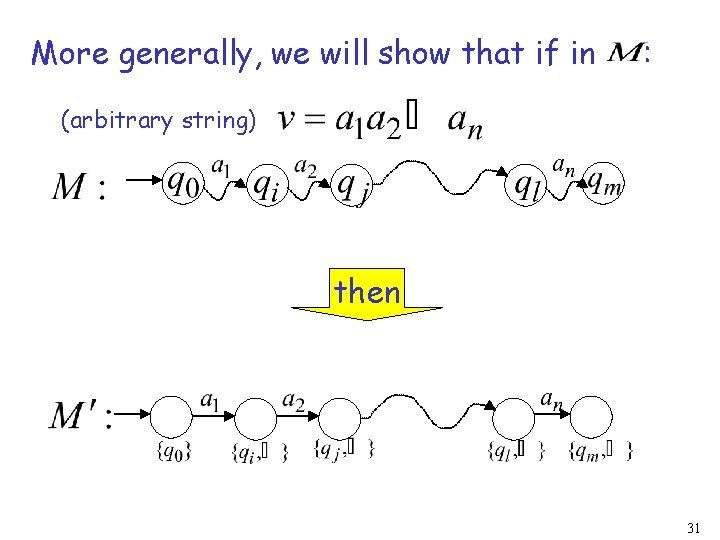
More generally, we will show that if in : (arbitrary string) then 31

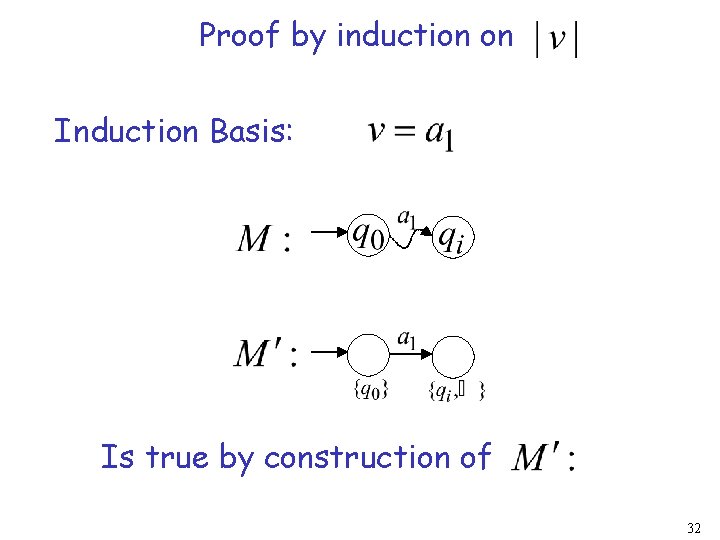
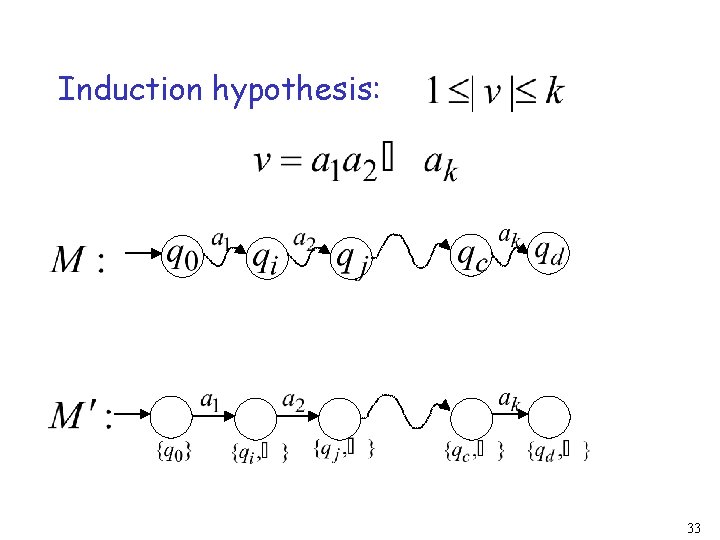
Proof by induction on Induction Basis: Is true by construction of 32

Induction hypothesis: 33

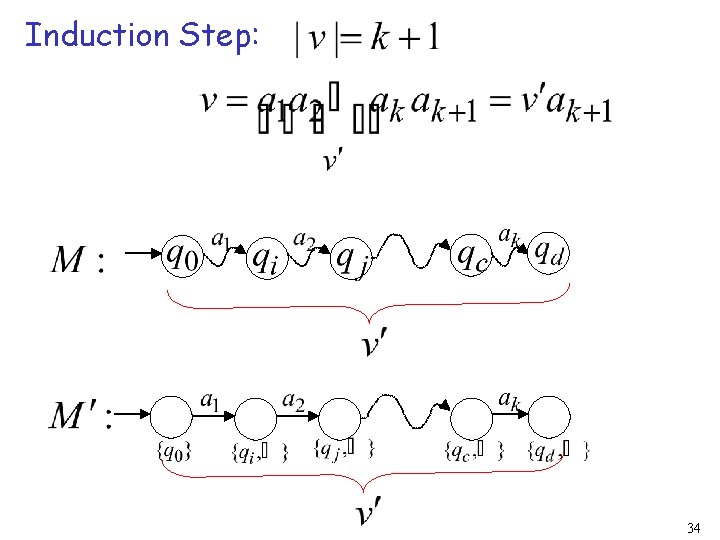
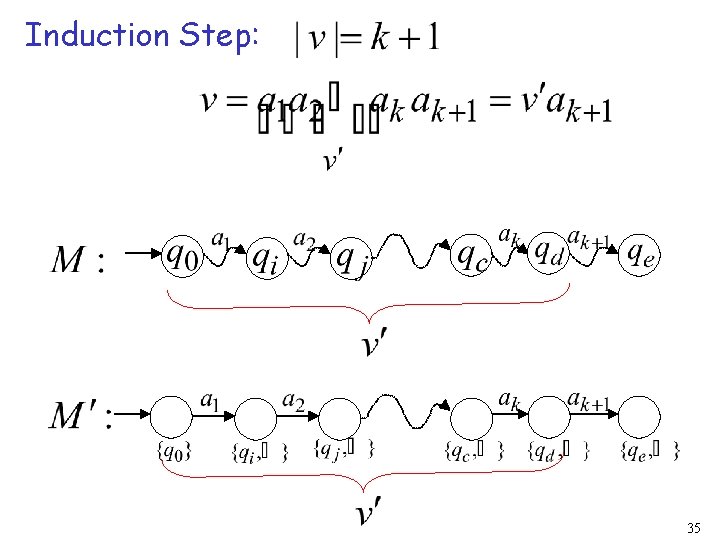
Induction Step: 34

Induction Step: 35

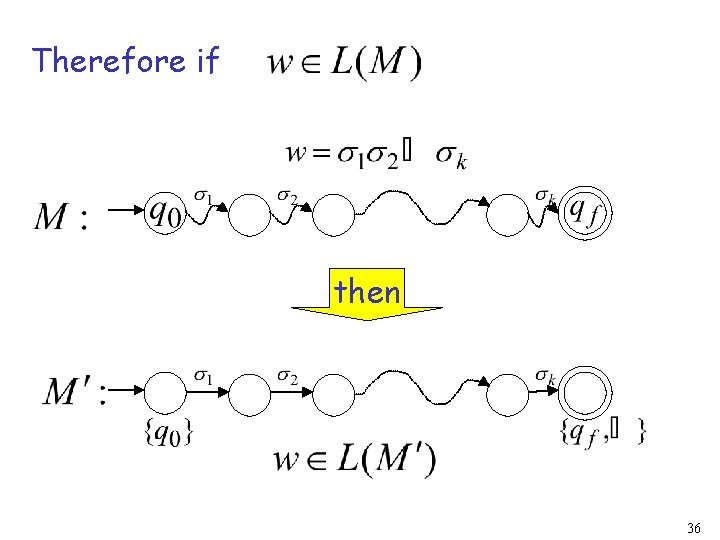
Therefore if then 36

We have shown: We also need to show: (proof is similar) 37

Single Accepting State for NFAs 38

Any NFA can be converted to an equivalent NFA with a single accepting state 39

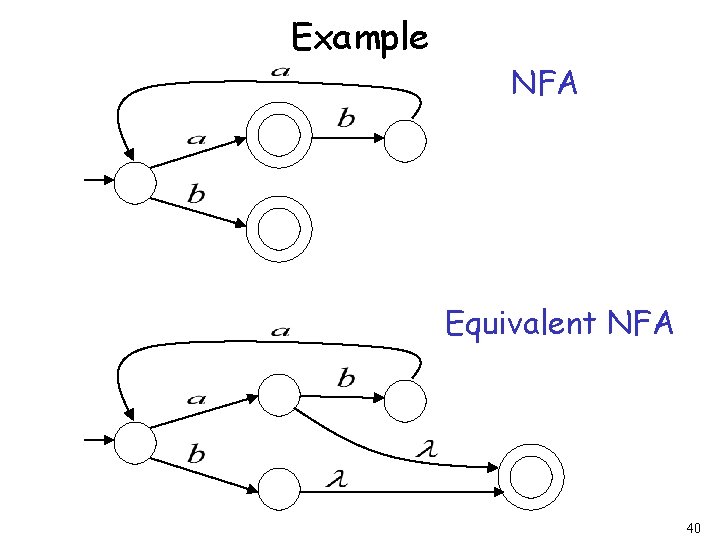
Example NFA Equivalent NFA 40

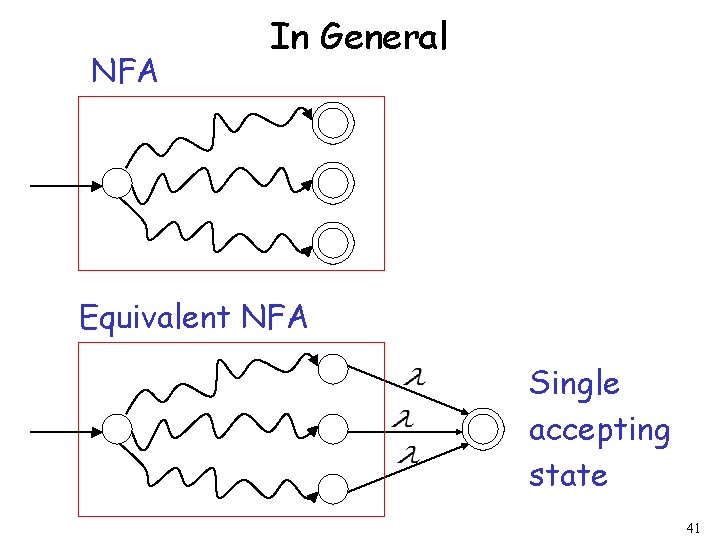
NFA In General Equivalent NFA Single accepting state 41

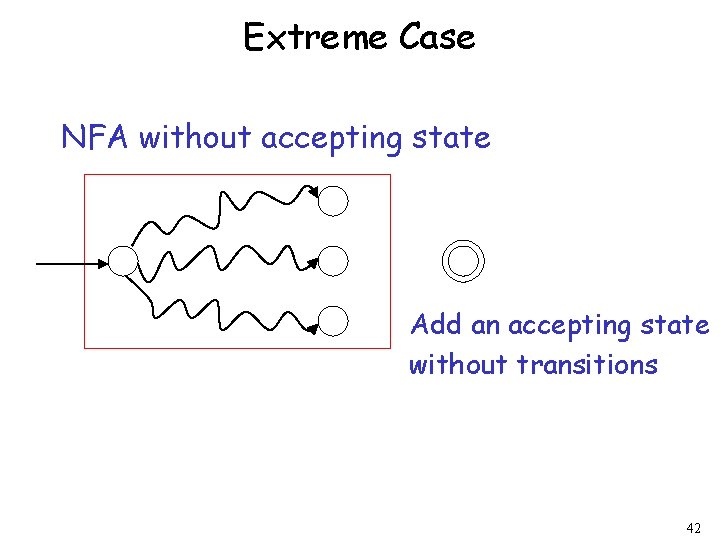
Extreme Case NFA without accepting state Add an accepting state without transitions 42

Properties of Regular Languages 43

For regular languages we will prove that: and Union: Concatenation: Star: Reversal: Are regular Languages Complement: Intersection: 44

We say: Regular languages are closed under Union: Concatenation: Star: Reversal: Complement: Intersection: 45

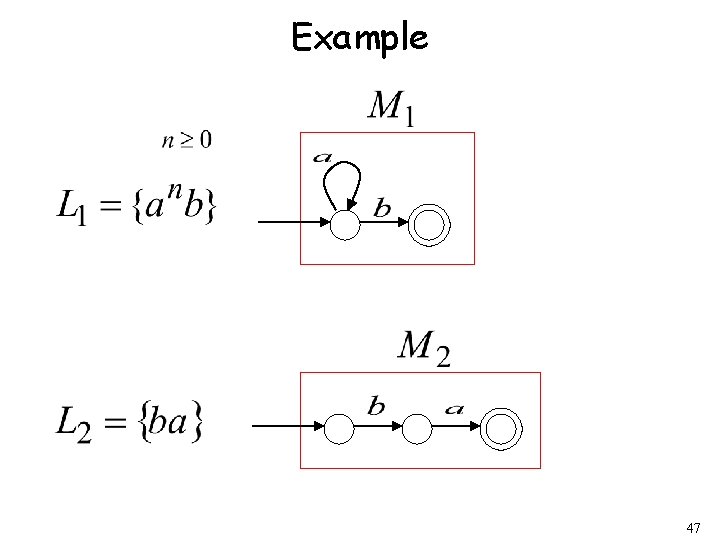
Regular language NFA Single accepting state Regular language NFA Single aceepting state 46

Example 47

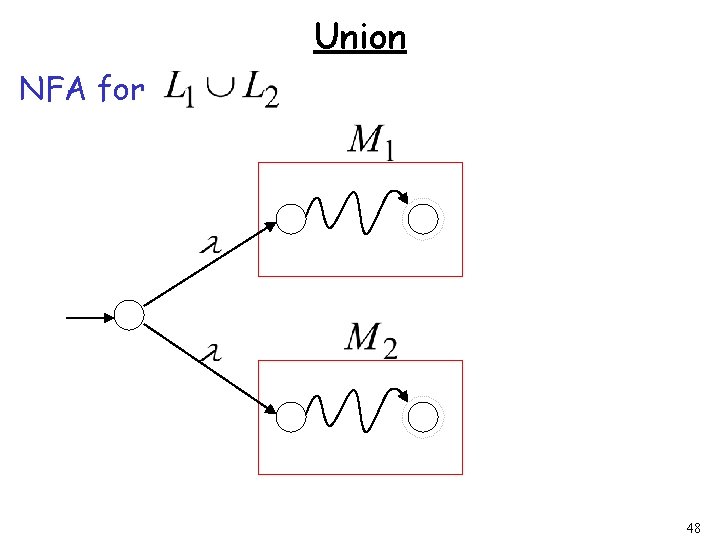
Union NFA for 48

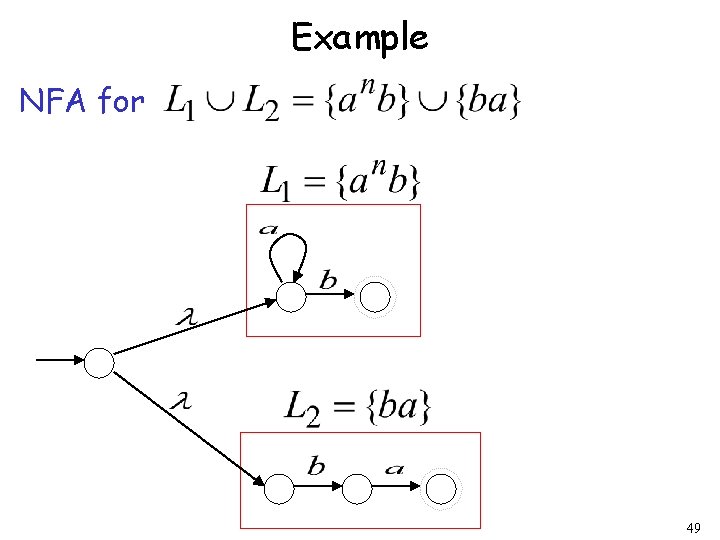
Example NFA for 49

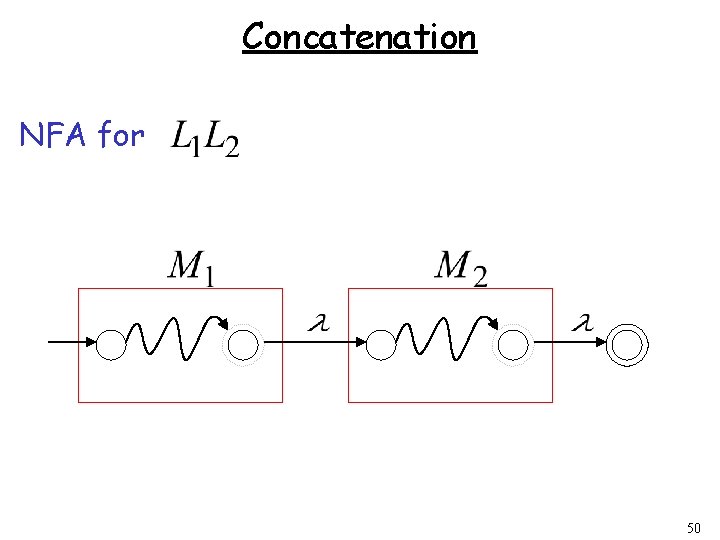
Concatenation NFA for 50

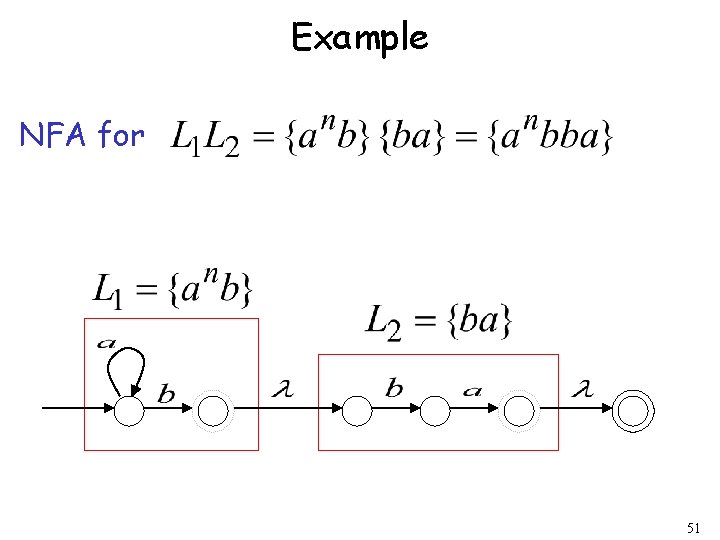
Example NFA for 51

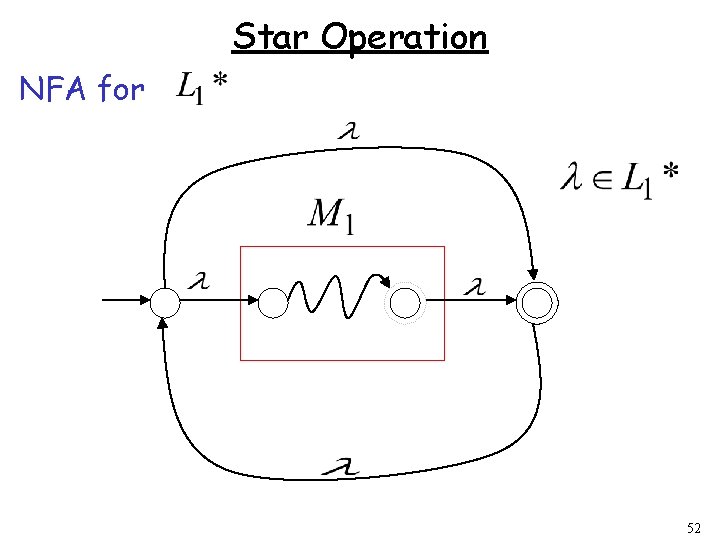
Star Operation NFA for 52

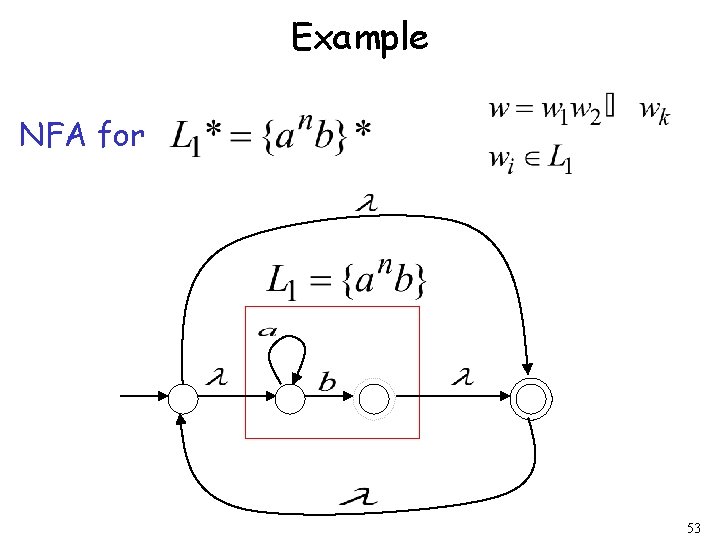
Example NFA for 53

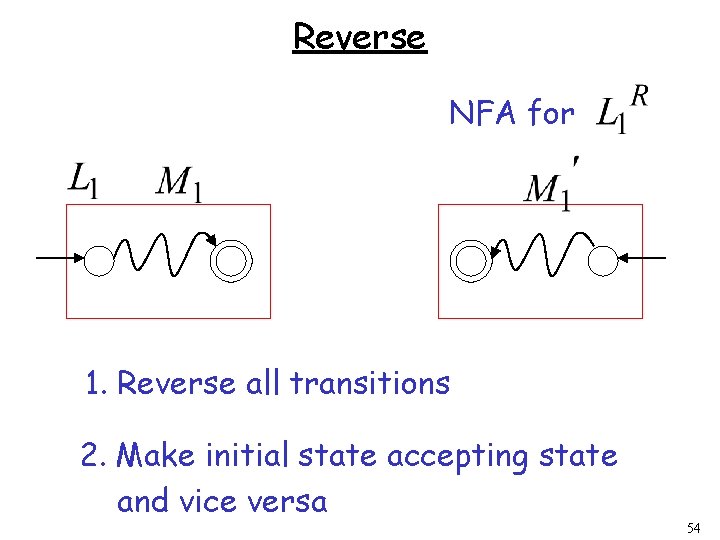
Reverse NFA for 1. Reverse all transitions 2. Make initial state accepting state and vice versa 54

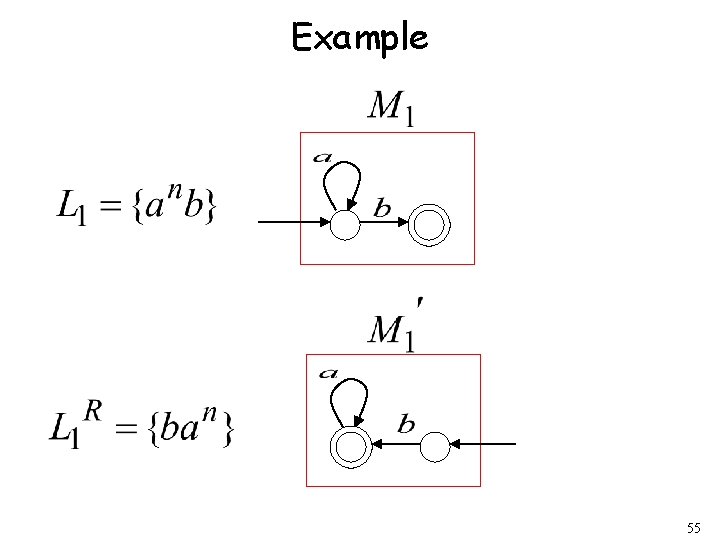
Example 55

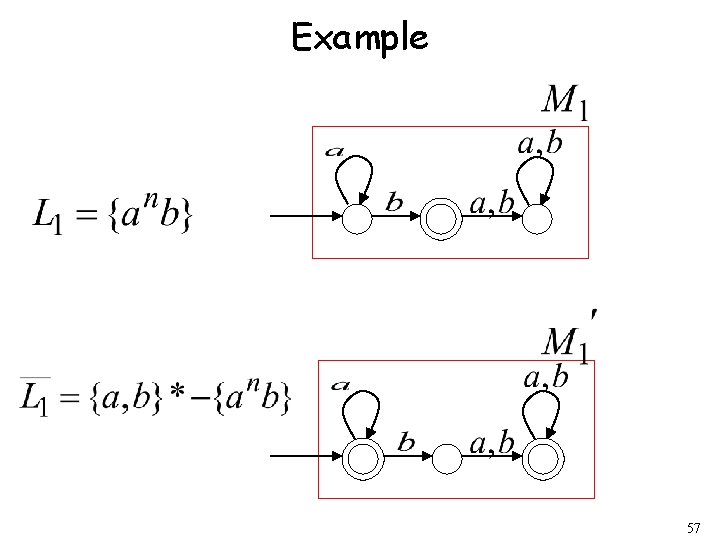
Complement 1. Take the FA that accepts 2. Make final states non-final, and vice-versa 56

Example 57

Intersection regular We show regular 58

De. Morgan’s Law: regular regular 59

Example regular 60

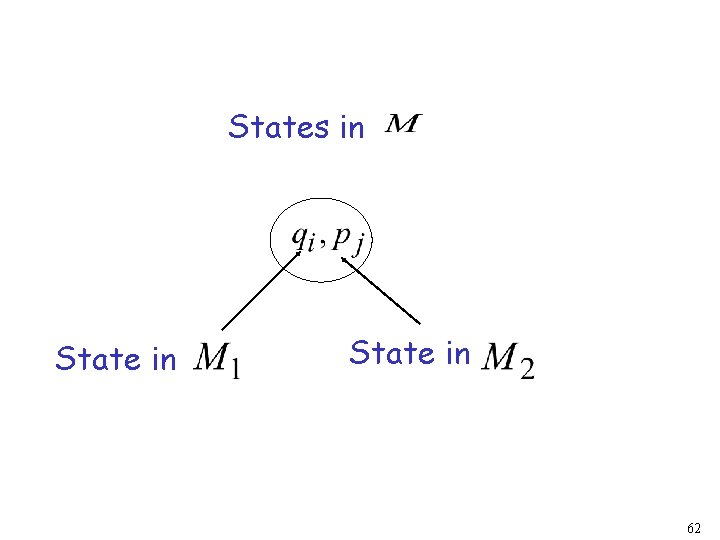
Another Proof for Intersection Closure Machine FA Machine for FA Construct a new FA that accepts simulates in parallel for and 61

States in State in 62

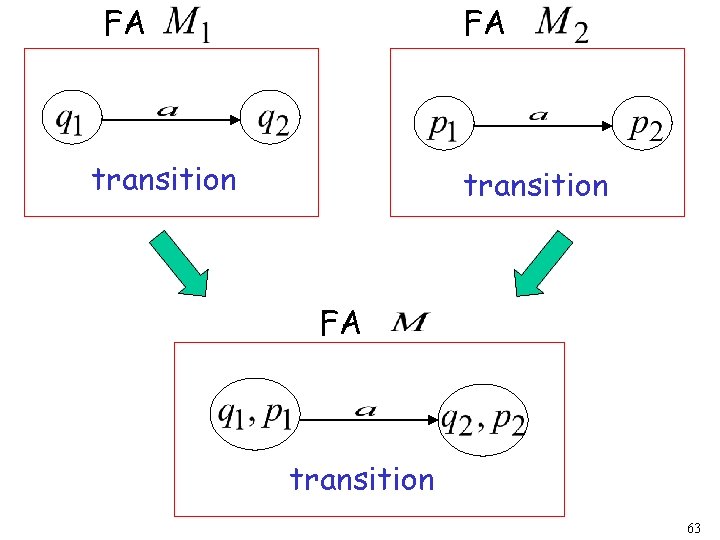
FA FA transition 63

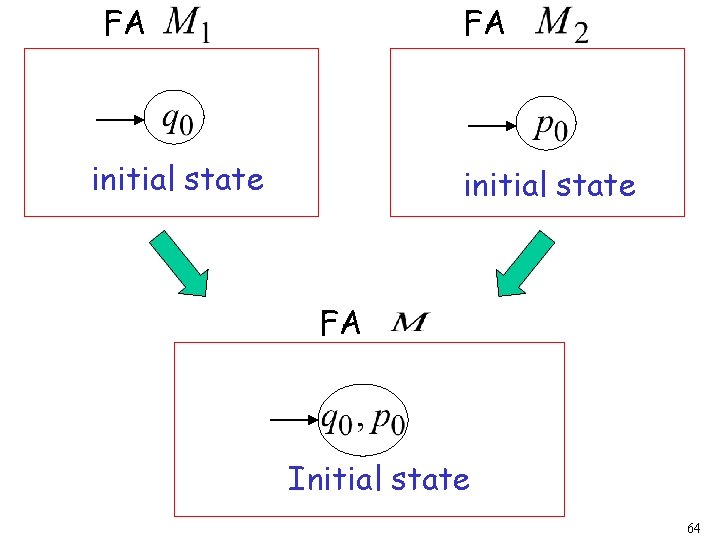
FA FA initial state FA Initial state 64

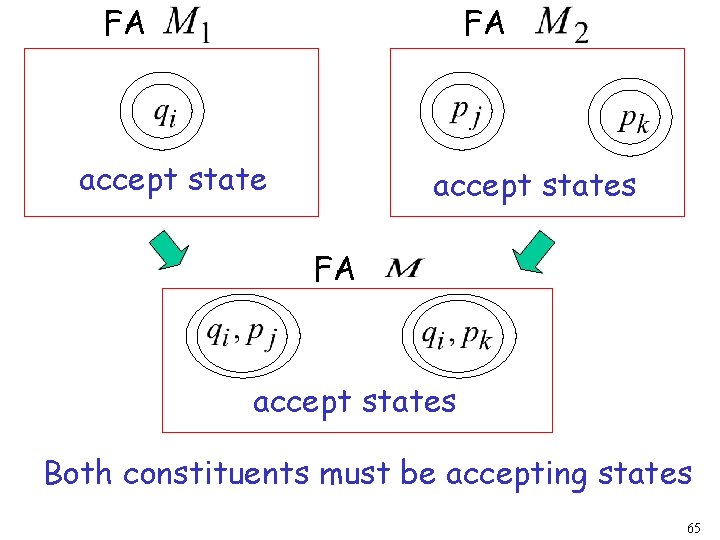
FA FA accept states Both constituents must be accepting states 65

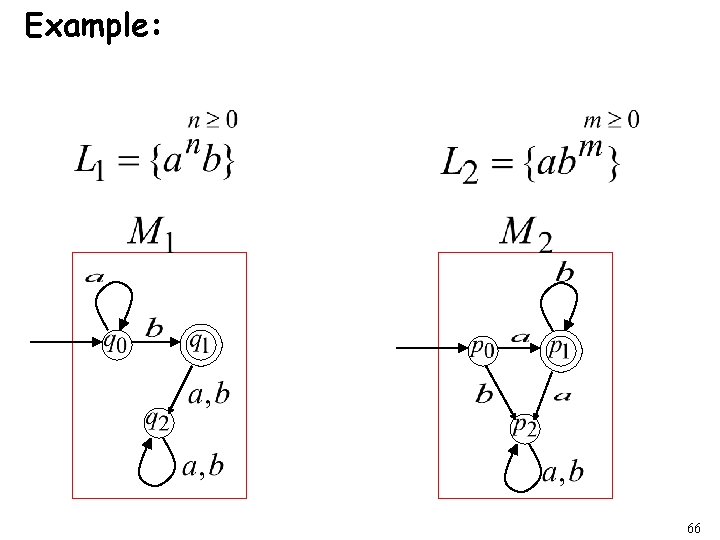
Example: 66

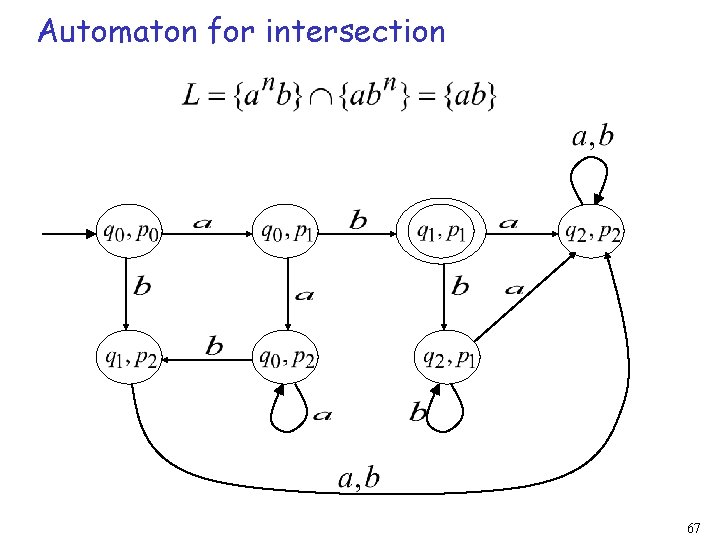
Automaton for intersection 67

simulates in parallel accepts string and if and only if accepts string and accepts string 68