Nexhat Makaj Arsimtar i matematiks SHFMU Mic SOKOLI

Nexhat Maçkaj Arsimtar i matematikës SHFMU “ Mic SOKOLI”

Objectivat o ü ü ü Në fund të orës nxënësit duhet të jenë në gjendje: Të kuptojnë vektorët me vetitë e tij. Të gjejnë shumën e vektorëve. Të analizojnë shumën e vektoritëve të kundërtë

Mjetet e nevojshme : o o o o Video projektori Laptopi Kompasi Lapsi Trekëndëshi Fletoret Tabela e zezë

Vektori eshte segmenti i orientuar me piken e fillimit dhe piken e mbarimit. Vektori ka Drejtimin, kahjen me shigjet. Distanca ndermjet pikes se fillimit A dhe pikes se mbarimit B quhet intensitet i vektorit Vektori me intesitet, drejtim te njejte dhe kahje te kundert quhet vektor i kundert. A (origjina) AB B (fundi) A (fundi) BA B (origjina)

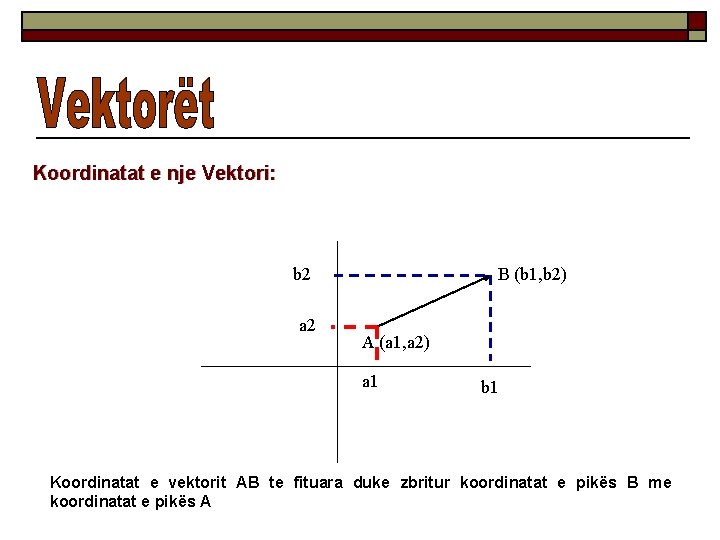
Koordinatat e nje Vektori: b 2 a 2 B (b 1, b 2) A (a 1, a 2) a 1 b 1 Koordinatat e vektorit AB te fituara duke zbritur koordinatat e pikës B me koordinatat e pikës A

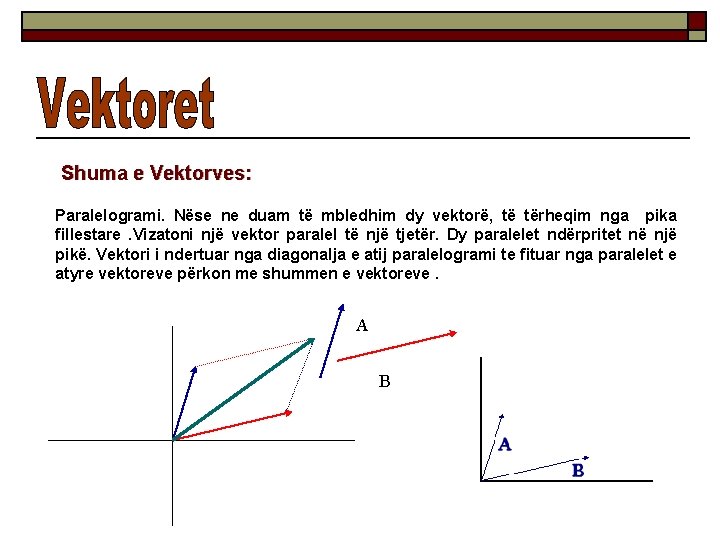
Shuma e Vektorves: Paralelogrami. Nëse ne duam të mbledhim dy vektorë, të tërheqim nga pika fillestare. Vizatoni një vektor paralel të një tjetër. Dy paralelet ndërpritet në një pikë. Vektori i ndertuar nga diagonalja e atij paralelogrami te fituar nga paralelet e atyre vektoreve përkon me shummen e vektoreve. A B

Shuma ee Vektoreve: Poligoni. Është përdorur, veçanërisht kur dëshirojnë për të mbledhur vektorët të ndryshme në të njëjtën kohë. Në fund të vektorit të parë është vendosur nën pikën e dytë në fund të vektorit të dytë është vendosur në pikën e tretë dhe kështu me radhë derisa të gjithë të përfundojë hartimin e vektorëve. Vektori rezulton është marrë duke u bashkuar me pikën e parë të te fillimit në fund të vektorit te fundit

Shuma e Vektoreve: Analizoni shumen e vektoreve me koordinata. A = (0, 5) B = (5, 4) A + B = (0, 5) + (5, 4) = (0 + 5, 5 + 4) = (5, 9)

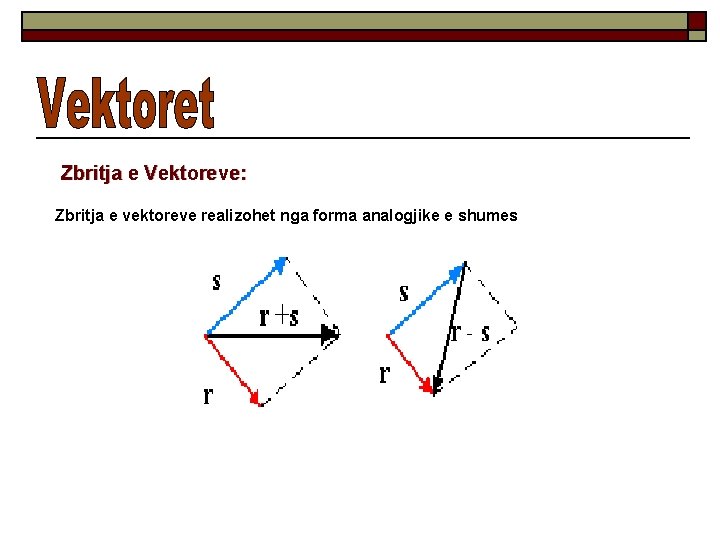
Zbritja e Vektoreve: Zbritja e vektoreve realizohet nga forma analogjike e shumes

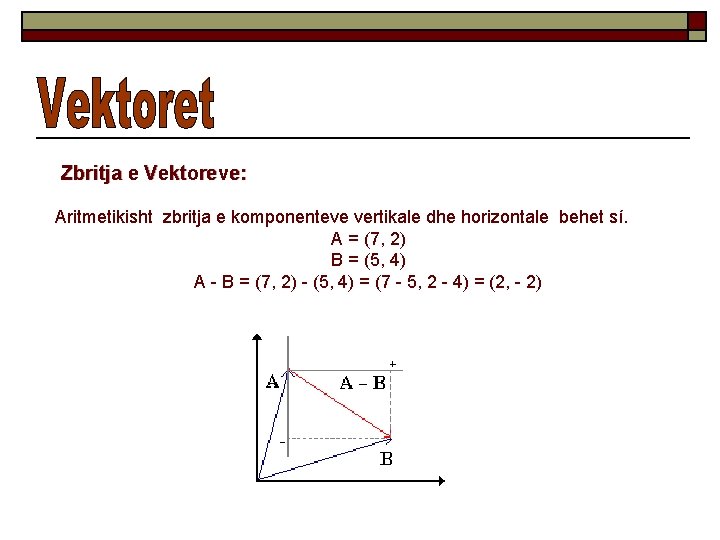
Zbritja e Vektoreve: Aritmetikisht zbritja e komponenteve vertikale dhe horizontale behet sí. A = (7, 2) B = (5, 4) A - B = (7, 2) - (5, 4) = (7 - 5, 2 - 4) = (2, - 2)

Vetite e shumes se Vektoreve: Komutatve a+b=b+a Asociative (a + b) + c = a + (b + c) Elementi i zero vektorit a+0=0+a=a Elementi i vektorit te kundert(simetrik) a' a + a' = a' + a = 0 a' = -a

Prodhimi ( shumezimi) i vektorit: Prodhimi i vektorit me numer behet duke shumezuar ate vektor me ate numer Prodhimi I vektoreve me pika koordinative behet duke i shumezuar koponentet e para me komponentet e para dhe te dytat me te dyta. Psh (-3, 2) x (5, 1) = ((-3) x 5) +(2 x 1) = -15+2 = -13 Vetite e Prodhimit dhe Shumes se Vektoreve: Komutative A*b=b*a Asociative (a + b) * c = a * (b + c)

Ju faleminderit!!! Nexhat Mackaj Sh. F. M. U “ Mic Sokoli” Lubiqevë nexhatmackaj@hotmail. com