Newtons Second Law of Motion Physics Chapter 6

Newton’s Second Law of Motion Physics Chapter 6

Newton’s Second Law of Motion Newton’s second law deals with forces and acceleration. n Acceleration (a) is a change in velocity in a time interval. n a = ∆v / ∆t n Unbalanced forces are ALWAYS the cause of acceleration. n

Force Causes Acceleration When an unbalanced force (a nonzero net force) is applied, acceleration occurs. n Acceleration depends upon the net force. n To increase acceleration, must increase net force. n Therefore, acceleration is directly proportional to net force. (Newton’s 2 nd Law a = F/m; more about mass in a bit ) n If net force doubles, then acceleration doubles. n

Mass & Acceleration is also dependent upon the inertia of the object. n The amount of acceleration of an object is dependent both on force applied & mass being pushed. n The same force applied to twice the mass produces half the acceleration. n Therefore, acceleration is inversely proportional to mass, or a = 1/mass. Again, a = F/m or Newton’s 2 nd Law n

Newton’s Second Law of Motion n Newton’s second law states, “The acceleration of an object is directly proportional to the net force acting on the object, in the direction of the net force, & is inversely proportional to the mass of the object. ” or, Acceleration = force / mass n Acceleration of an object is always in the direction of the net force. n

Revisiting Free Fall n n n When an object falls without the effects of friction or air resistance, it is called free fall. During each second of free fall, an object will accelerate at 9. 8 or 10 m/s/s, the pull of gravity (g). Therefore velocity of a falling object is found by using, n Velocity = gravity x time or v = gt

Free Fall: How Far? n Distance traveled = ½ (acceleration x time) nd n n = ½ gt 2 Air resistance can effect how an object falls in the real world. However this equation is accurate for most objects falling from a position of rest. We disregard air resistance for the most part.

Friction and Terminal Velocity n n n When friction is present an object may move at a constant velocity even when a force is applied to it. This occurs when the applied force just balances the friction force. Therefore, net force equals zero and the object is at equilibrium. If an object is at equilibrium, no acceleration occurs. This is ‘terminal velocity’ as there is no acceleration

Acceleration & Free Fall n n n If an object is falling toward Earth and is only acted upon by the force of gravity and air resistance is negligible, then the object is in free fall. The greater the mass of the object, the greater the gravitational force between the object & Earth. Inertia is the resistance to change in an object’s motion. n Therefore an object that has twice the mass, may have twice the force, but it also has twice the inertia. n In free fall, the increase balances out and all objects fall at the same acceleration, irregardless of mass.

Acceleration with Air Resistance n n Friction is not restricted to solids, but also occurs in fluids such as liquids and gases. Fluid friction is friction that occurs as an object pushes aside the fluid it is moving through. Air resistance is a very common form of fluid friction. In air resistance, the net force is less than the weight. It is the weight minus air drag.

Remember all objects fall at the speed…. . Not so if you figure in air resistance! n n The force of air drag depends upon frontal area of the falling object AND upon its speed. Why? The greater the speed, the more air molecules an object encounters per second. Therefore, terminal velocity depends on mass, cross sectional area, & drag coefficient as well as the density of the air/fluid thru which object falls as well as gravitational acceleration (which is more for larger masses). Differences in mass and other properties will result in different terminal velocities, so larger masses have

Terminal Velocity, to sum up…. When the net force of a falling object reaches zero, the object stops accelerating. n The speed at which acceleration terminates is called the terminal speed or terminal velocity. n n At terminal velocity, the downward forces (gravity) and upward forces (air resistance) are balanced.

Air Resistance and Sky Diving n n The terminal speed for sky divers varies from 150200 km/h. It depends upon the weight and orientation of the diver. A heavier diver will obtain a greater terminal velocity than a lighter diver. More air is encountered when a body is spread out and air resistance is increased, thus terminal velocity is lowered.

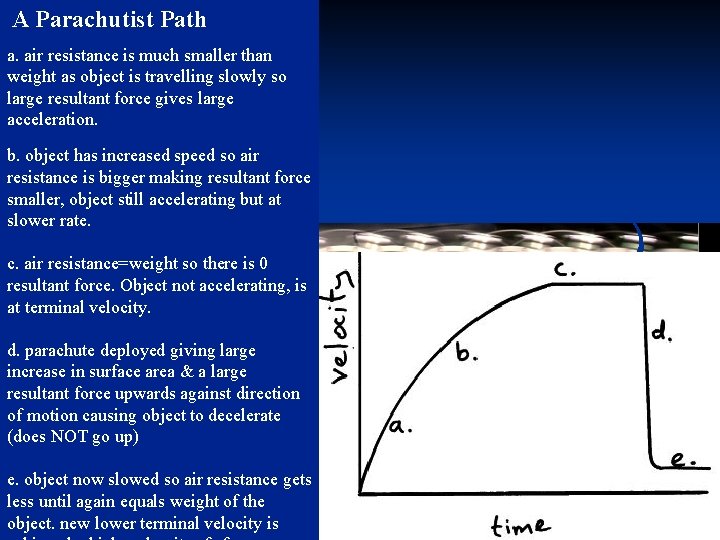
A Parachutist Path a. air resistance is much smaller than weight as object is travelling slowly so large resultant force gives large acceleration. b. object has increased speed so air resistance is bigger making resultant force smaller, object still accelerating but at slower rate. c. air resistance=weight so there is 0 resultant force. Object not accelerating, is at terminal velocity. d. parachute deployed giving large increase in surface area & a large resultant force upwards against direction of motion causing object to decelerate (does NOT go up) e. object now slowed so air resistance gets less until again equals weight of the object. new lower terminal velocity is

Sample Problem #1 Suzie exerts a horizontal force of 15 N on a box with a mass of 10 kg on a frictionless floor. What is the acceleration of the box? Remember a = F / m & a N is = kg m/s 2 So 15 N/ 10 kg = 15 kg m/s 2 10 kg = 1. 5 m/s 2

Sample Problem #2 n Helen exerts a force of 5. 0 N on a hockey puck with a mass of 0. 5 kg. The ice has a friction of 1. 0 N. What is the acceleration of the hockey puck? a = F / m or 5 – 1 N / 0. 5 kg = 2 m/s 2

Sample Problem #3 Calculate the force needed to accelerate a 210 kg motorcycle from 12. 5 m/s to 20. 8 m/s in 6. 9 seconds. We have the time & want to find the force, F, but need the acceleration to calculate F in the equation: a = F / m Since acceleration is: a = Δ v / Δ t Then to find it, use a = vf – vi Δ t So a = 20. 8 – 12. 5 m/s = 1. 2 m/s/s 6. 9 s Then since F = m a plug & chug. . = (1. 2 m/s 2) 210 kg = 252 N

Sample Problem #4 Car A has a mass of 2000 kg and experiences a force of 4000 N. Car B has a mass of 1000 kg and experience a force of 2000 N. Which car experiences a greater acceleration? Which car has more inertia? Use the equation a = F / m Car A’s a = (4000) / 2000 = 2 m/s/s Car B’s a = (2000) / 1000 = 2 m/s/s

Sample Problem #5 Calculate the acceleration of a falling parachutist when the drag force is 300 N and the mass of the parachutist is 80 kg? Use A = F / m BUT have to find the NET force first. Parachutist’s WEIGHT is g m or 10 m/s/s)(80 kg) = 800 N So NET force is the weight – drag ( Fg - Fdrag ) or 800 - 300 N or 500 N THEN a = F / m or 500 N / 80 kg = 6. 25 m/s/s