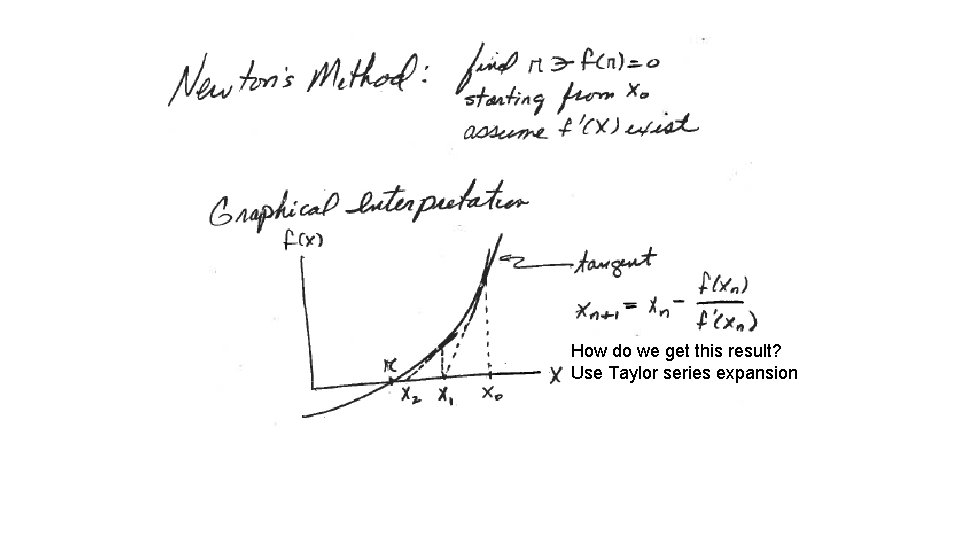
Newtons Method How do we get this result

Newton’s Method

How do we get this result? Use Taylor series expansion

Generalize to xk and xk+1

Develop a Mat. Lab code for Newton’s method 1) What is the basic idea? 2) Put basic idea into a pseudocode 3) Translate pseudocode into Mat. Lab syntax

Develop a pseudocode for Newton’s Method xk+1 = xk – f(xk)/f’(xk) Basic idea behind calculation; Given initial guess and equations for f(x) and f’(x) calculate sequence x 1, x 2, … xk, xk+1, … set x 1 to the initial guess stop when change xk-> xk+1 is small assign root to xk+1 calculate f(xk+1) to verify it is near zero

pseudocode for Newton’s method xk+1 = xk – f(xk)/f’(xk) function [r, fr]=newton(fh, dfh, x 0) Initialization steps = 0 x 1 = x 0 minre = convergence requirement on fractional change re = large initial value of fractional change while (re>minre) and (steps<maxsteps) increment steps save current estimate of root calculate next estimate of root re = absolute value of fractional change end while loop r = best estimate of root fr = fh(r) end function

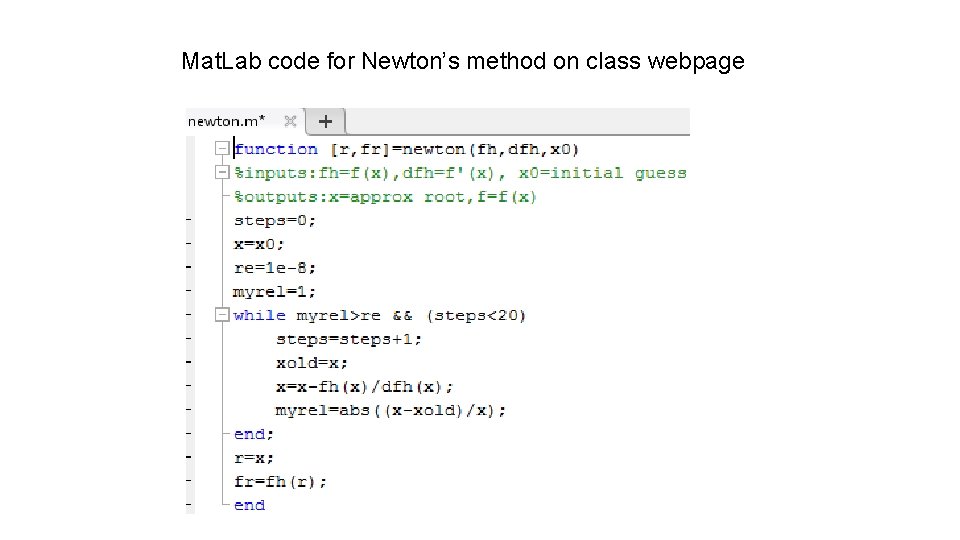
Mat. Lab code for Newton’s method on class webpage

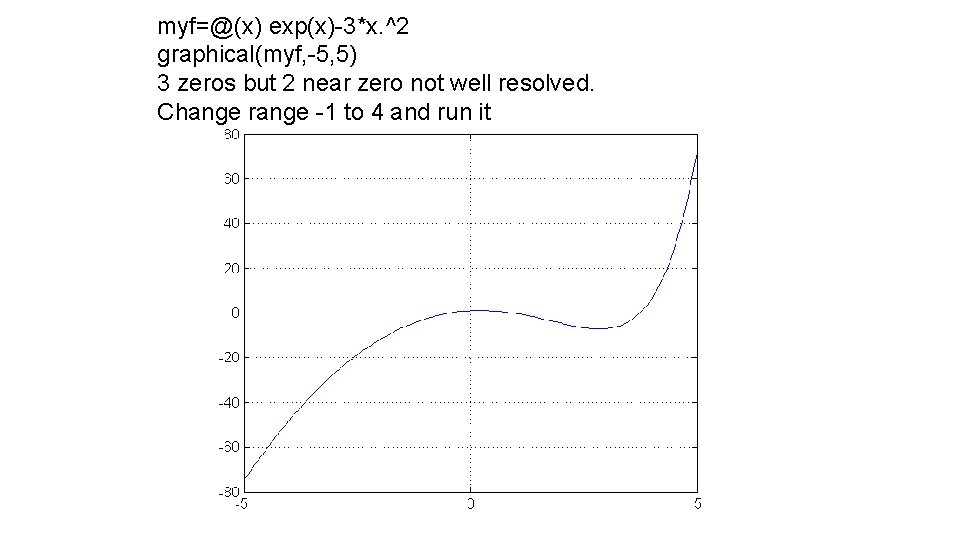
Write scripts to use graphical and newton to find all the values of x where the graphs of ex and 3 x 2 intersect. Start with a script for graphical Exponentials dominate polynomial; hence no intersections at large values of x. Both ex and 3 x 2 are non-negative; hence an intersection at negative values of x is possible. Initial range -5 to 5 Write script and run it

myf=@(x) exp(x)-3*x. ^2 graphical(myf, -5, 5) 3 zeros but 2 near zero not well resolved. Change range -1 to 4 and run it

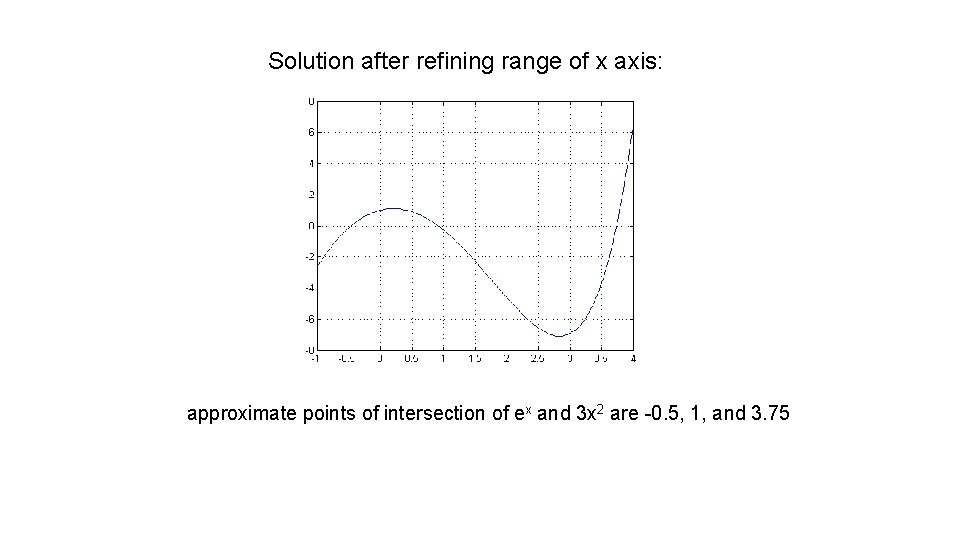
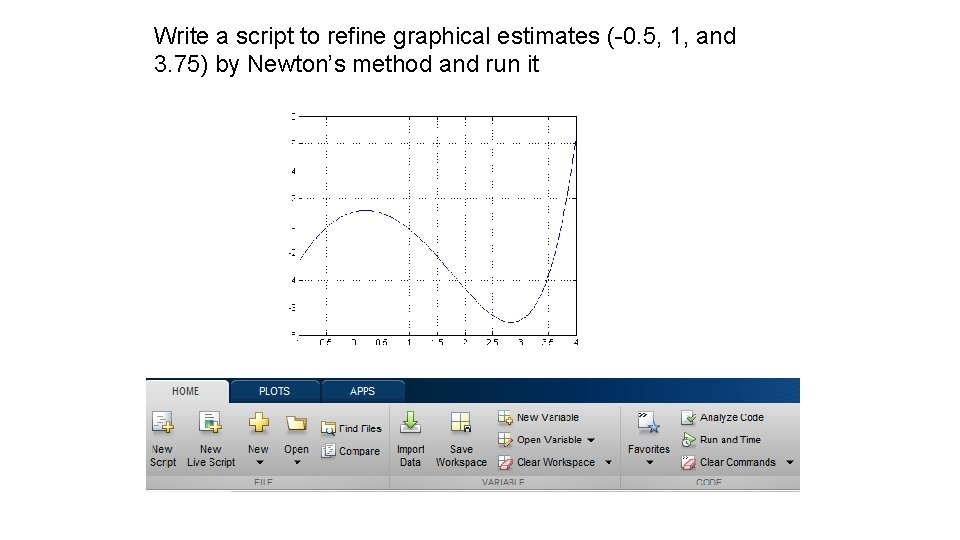
Solution after refining range of x axis: approximate points of intersection of ex and 3 x 2 are -0. 5, 1, and 3. 75

Write a script to refine graphical estimates (-0. 5, 1, and 3. 75) by Newton’s method and run it

Write a script to find all intersections of ex and 3 x 2 by Newton’s method. In the editor myf=@(x) exp(x)-3*x^2; mydf=@(x) exp(x)-6*x; [r 1, fr 1]=newton(myf, mydf, 0. 5); disp([r 1, fr 1]) [r 2, fr 2]=newton(myf, mydf, 1); disp([r 2, fr 2]) [r 3, fr 3]=newton(myf, mydf, 3. 7); disp([r 3, fr 3]) Copy, paste into the command window, and run

Script to refine multiple intersections of ex and 3 x 2 by Newton’s method copied to and run in the command window Now that you know the script runs successfully, you might want to save it. The script in the editor is called “Untitled”. If you want to keep it, use “save as” and rename.

Assignment 1 Estimate all the zeros of x 3 -x 2 -2 x+1 graphically. Hand in copies of your graph with estimates marked Use Newton’s method to improve estimates of zeros. Hand in a copy of command window that shows your script for using Newton’s method and results.

Derive expected convergence rate of Newton’s method

The convergence of Newton’s method is usually quadratic. Error in the n+1 estimate is proportional to the square of error in nth estimate. Proportionality constant is different for different initial guesses. Makes convergence slightly dependent on the initial guess. How do I change the newton function to get convergence data?

Modify this pseudocode to get convergence data function [r, fr]=newton(fh, dfh, x 0) Initialization steps = 0 x = x 0 minre = convergence requirement on fractional change re = large initial value of fractional change while (re>minre) and (steps<maxsteps) increment steps save current estimate of root calculate next estimate of root re = absolute value of fractional change end while loop r = best estimate of root fr = fh(r) end function

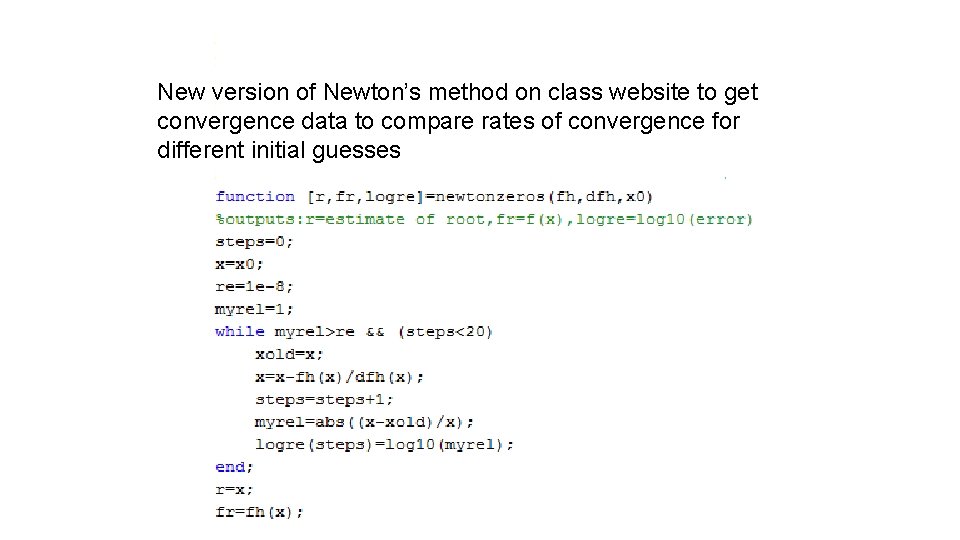
Extended pseudocode for Newton’s method function [r, fr, logre]=newton(fh, dfh, x 0) Initialization steps = 0 x = x 0 minre = convergence requirement on fractional change re = assign a large initial value of fractional change while (re>minre) and (steps<maxsteps) increment steps save current estimate of root calculate next estimate of root re <- absolute value of fractional change logre(steps)=log base 10(re) end while loop r = best estimate of root fr = fh(r) end function

Note alternative to “inline” New version of Newton’s method on class website to get convergence data to compare rates of convergence for Note suppressed output of logre different initial guesses

Write script to get convergence data for same root with different initial guesses How do we ensure convergence to the same root? Make a semi-log plot of convergence data How do we make a semi-log plot? Put results for both guesses on the same set of axes How do we put 2 graphs on the same axes?

Find intersections of ex and 3 x 2 by Newton’s method. For initial guesses 0. 5 and 1. 5, Newton’s method should converge to the zero near 1, since max and min separate these initial guesses from other zeros.

Since the convergence data. Note wasalternative saved as log 10(myrel), to “inline” we can use a linear plot. Note suppressed output of logre

Pseudocode for script to compare the convergence Newton’s method for different intial guesses define function handles for f(x) and f’(x) Call newtonzeros with initial guess 1 Save convergence data as array 1 Call newtonzeros with initial guess 2 Save convergence data as array 2 Disp([r 1, r 2]) to ensure convergence to same aero Call plot(array 1) Note: just one argument hold on Call plot(array 2) hold off Write a script specific to the intersection of ex and 3 x 2 near 1 with initial guesses 0. 5 and 1. 5. Run it.

Script to compare convergence of Newton’s method disp([r 1, r 2])

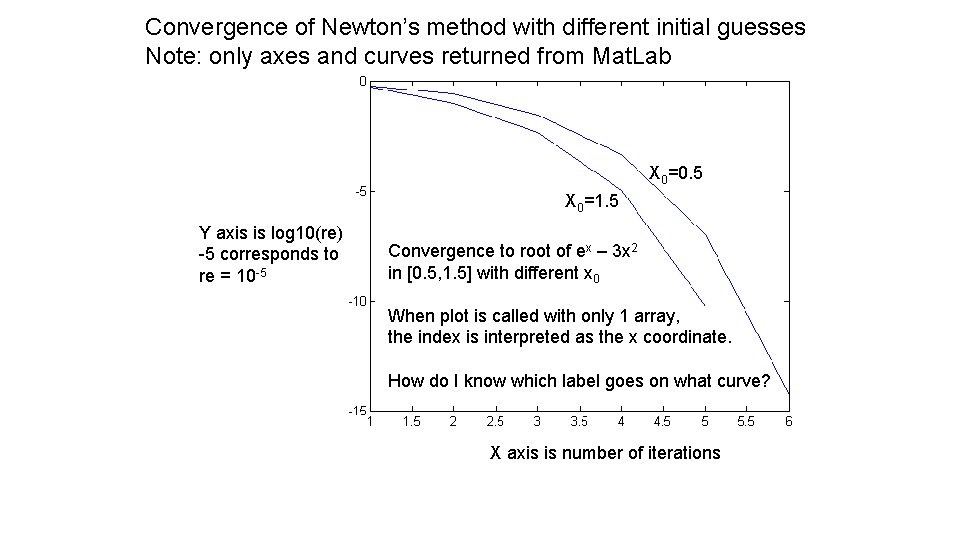
Convergence of Newton’s method with different initial guesses Note: only axes and curves returned from Mat. Lab X 0=0. 5 X 0=1. 5 Y axis is log 10(re) -5 corresponds to re = 10 -5 Convergence to root of ex – 3 x 2 in [0. 5, 1. 5] with different x 0 When plot is called with only 1 array, the index is interpreted as the x coordinate. How do I know which label goes on what curve? X axis is number of iterations

Assignment 2 f(x) = ex - 3 x 2 has a zero in the interval [-1, 0]. Download newtonzeros. m from class webpage. Use plot to compare the rates of convergence to the root with initial guesses 0 and -1. Verify that both initial guesses converge to the same zero. Hand in a copy of command window where Newton’s method was called Hand in your plot with labels (by hand is OK) on axes and curves to show which curve goes with which initial guess.

Note alternative to “inline” This code uses relative change in root as the convergence criterion. Note suppressed output of logre What happens when the root you are seeking is zero?

Don’t need a numerical method to find roots of the cubic y = x 3 -x 2 -2 x. Find roots by factoring. y = x(x 2 -x-2) = x(x+1)(x-2). Factoring shows roots are -1, 0, and 2 What happens when you use Newton method to find these roots?

y = x 3 -x 2 -2 x roots -1, 0, 2 Root at zero Initial guess = 0. 75