Newtons Laws Inertia Force Action and Reaction Dr

Newton’s Laws: Inertia, Force, Action and Reaction Dr. Walker

Equilibrium • Objects which are in balance with each other are in equilibrium – These objects are stable and will not move if undisturbed – An external interaction (for example: pushing, pulling) is required to make the object unstable http: //imgur. com/TDJDnaa

May The Force Be With You… • A force is a push or pull – A force is required to change the state of motion (start, stop, alter direction) of an object – Net force = sum of all forces acting on an object – Unit force = newton (N) – 1 kg x 9. 8 m/s 2 = 9. 81 N = 2. 205 lbs http: //aven. amritalearning. com/userfiles/1/image/force 2. jpg

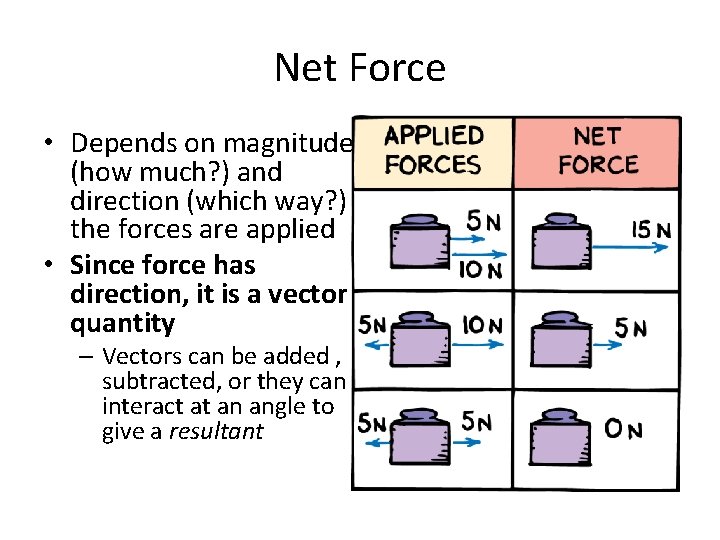
Net Force • Depends on magnitude (how much? ) and direction (which way? ) the forces are applied • Since force has direction, it is a vector quantity – Vectors can be added , subtracted, or they can interact at an angle to give a resultant

Interaction Forces – Fundamental Forces • Gravity • Electromagnetism • Strong Nuclear Force • Weak Nuclear Force http: //hyperphysics. phy-astr. gsu. edu/hbase/Forces/funfor. html

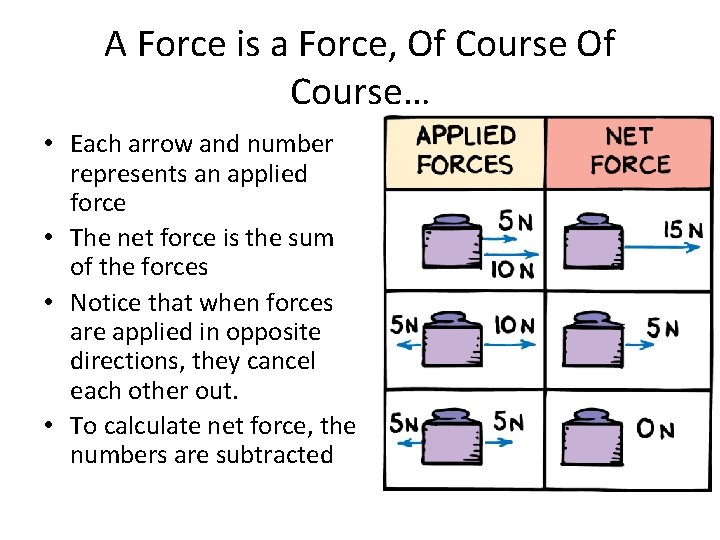
A Force is a Force, Of Course… • Each arrow and number represents an applied force • The net force is the sum of the forces • Notice that when forces are applied in opposite directions, they cancel each other out. • To calculate net force, the numbers are subtracted

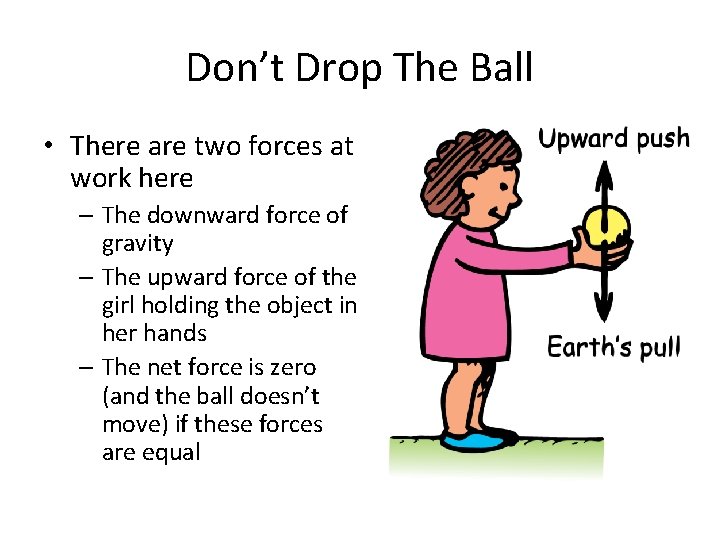
Don’t Drop The Ball • There are two forces at work here – The downward force of gravity – The upward force of the girl holding the object in her hands – The net force is zero (and the ball doesn’t move) if these forces are equal

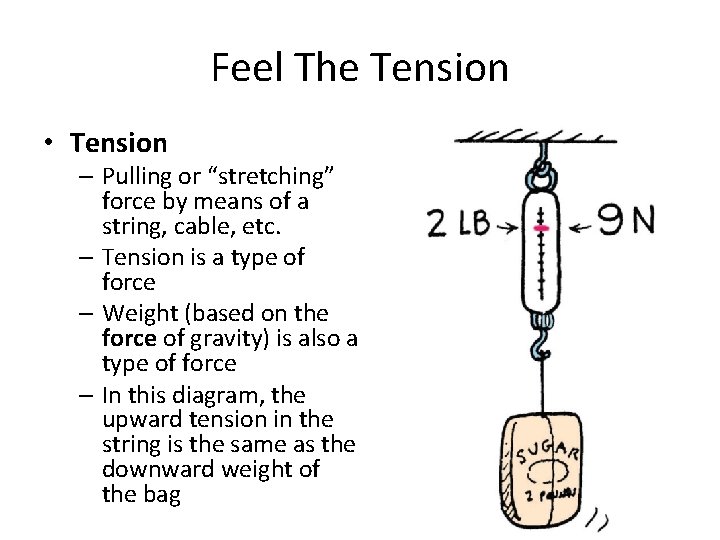
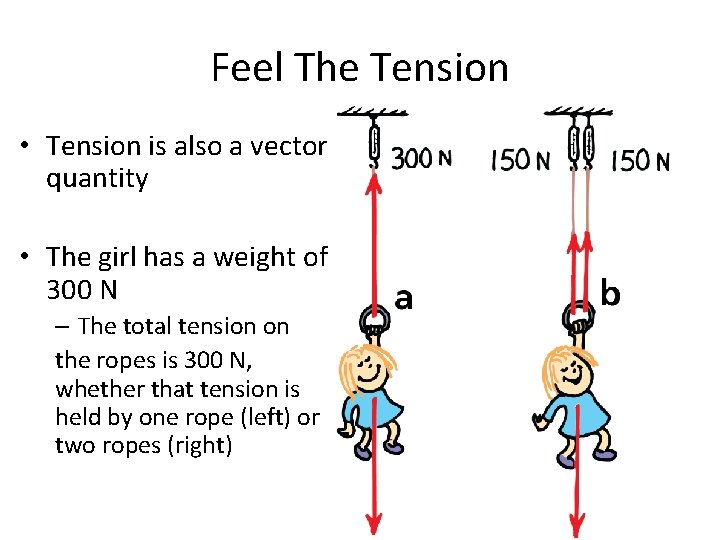
Feel The Tension • Tension – Pulling or “stretching” force by means of a string, cable, etc. – Tension is a type of force – Weight (based on the force of gravity) is also a type of force – In this diagram, the upward tension in the string is the same as the downward weight of the bag

Feel The Tension • Tension is also a vector quantity • The girl has a weight of 300 N – The total tension on the ropes is 300 N, whether that tension is held by one rope (left) or two ropes (right)

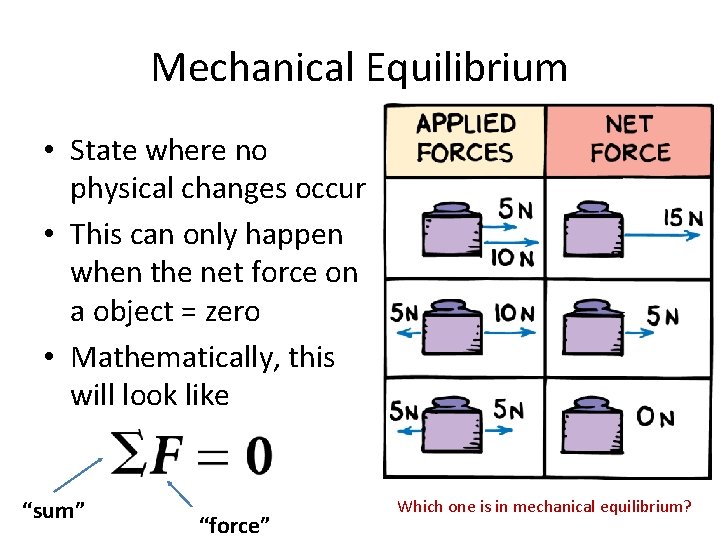
Mechanical Equilibrium • State where no physical changes occur • This can only happen when the net force on a object = zero • Mathematically, this will look like “sum” “force” Which one is in mechanical equilibrium?

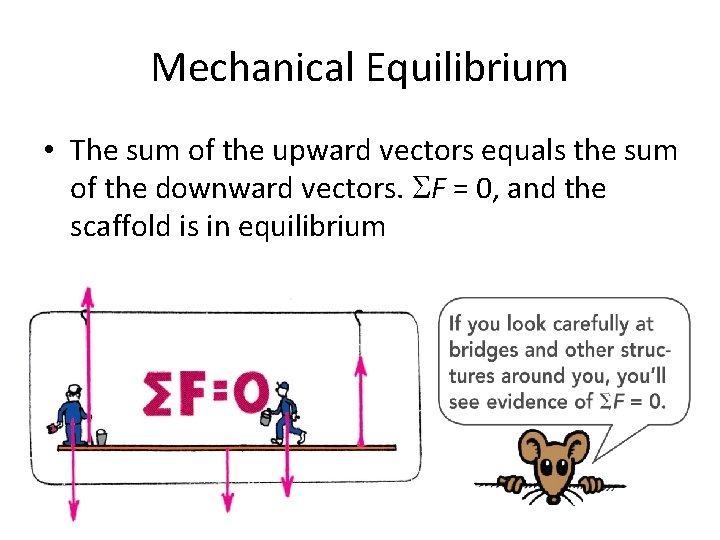
Mechanical Equilibrium • The sum of the upward vectors equals the sum of the downward vectors. F = 0, and the scaffold is in equilibrium

Force Example – Two horizontal forces of 225 N and 165 N are exerted in the same direction on a crate. What is the net force on the crate? – Is this system in equilibrium?

Force Example – Two horizontal forces of 225 N and 165 N are exerted in the same direction on a crate. What is the net force on the crate? 225 N 390 N 165 N – This system is NOT in equilibrium because there is a net force on the crate (it’s not 0!)

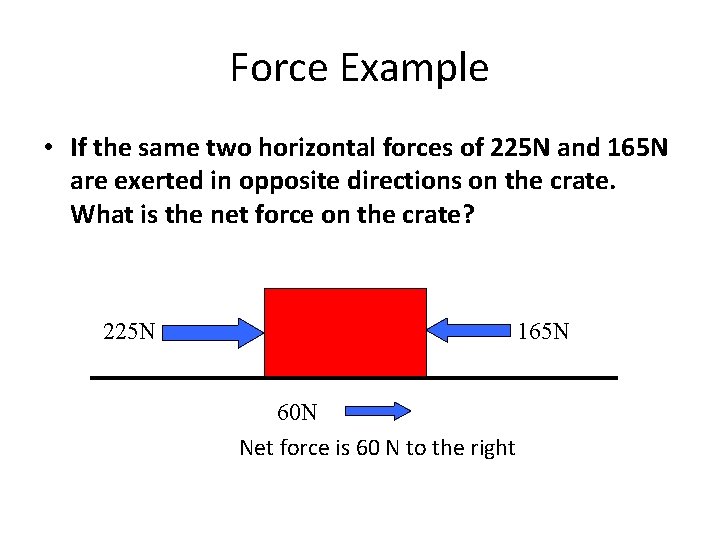
Force Example • If the same two horizontal forces of 225 N and 165 N are exerted in opposite directions on the crate. What is the net force on the crate?

Force Example • If the same two horizontal forces of 225 N and 165 N are exerted in opposite directions on the crate. What is the net force on the crate? 225 N 165 N 60 N Net force is 60 N to the right

Support Force • What forces act on a book lying at rest on a table? – One is the force due to gravity—the weight of the book. – There must be another force acting on it to produce a net force of zero—an upward force opposite to the force of gravity • The upward force that balances the weight of an object on a surface is called the support force. – A support force is often called the normal force. – The support force comes from the table

Moving Objects • An object moving at constant speed in a straightline path is also in a state of equilibrium. Once in motion, if there is no net force to change the state of motion, it is in equilibrium. – Remember, a constant speed in a straight line path in velocity – An object with a constant velocity has no acceleration – No outside force, no acceleration

Newton • Refers to Sir Isaac Newton (1642 -1727) • Developed theory of universal gravitation and the laws of motion • Developed differential calculus with Gottfried Liebniz for the purpose of studying physics • The Newton (metric unit of force) is named for him

Newton’s First Law • Newton’s First Law of Motion – “Every Body Continues In Its State of Rest, Or of Uniform Motion In A Straight Line, Unless It is Compelled to Change That State by Forces Impressed Upon It. ” – Aka “The Law of Inertia”

Definitions • Inertia – The Tendency of an Object to Resist a Change in Movement – Mass is a Measurement of Inertia • More mass, more inertia • Equilibrium – Net Force ( ) = 0

Inertia • Inertia simplified • Objects in a state of rest tend to remain at rest. • Only a force will change that state. • Objects don’t start moving by themselves • Objects in motion will retain that motion unless acted on by a force • A car stops because of the force (friction) of the brake pedal or the road on the tires • The heavier the car is, the longer it will take to roll to a stop

Newton’s Second Law • Newton’s Second Law of Motion – “The Acceleration of a Body is Directly Proportional to the Net Force Acting on the Body and Inversely Proportional to the Mass of the Body. ” • Translation – more force = more acceleration, less force = less acceleration • Acceleration = change in velocity/change in time

Measuring Force • • F – Force (N) m – mass (kg) – NOT grams, kilograms! a – acceleration (m/s 2) 1 N = 1 kg *m/s 2 – Just like the formula!

Calculating Force • On Earth, a scale shows that Ben weighs 712 N. What is Ben’s mass?

Calculating Force • On Earth, a scale shows that Ben weighs 712 N. What is Ben’s mass? • F = ma • 712 N = m (9. 8 m/s 2) • m = 72. 7 kg (160 lbs)

Calculating Force – The acceleration of gravity on the moon is 1. 60 m/s 2. What would the scale indicate that Ben weighs if he were on the moon and his mass is the same as the previous question? (72. 7 kg)

Calculating Force – The acceleration of gravity on the moon is 1. 60 m/s 2. What would the scale indicate that Ben weighs if he were on the moon and his mass is the same as the previous question? (72. 7 kg) 116. 3 N = 26. 1 lbs!!

Calculating Force Example • If you hold a 1. 0 lb object using 6. 5 N of upward force, what is the net force on the object? (1 lb = 0. 454 kg)

Calculating Force Example • If you hold a 1. 0 lb object using 6. 5 N of upward force, what is the net force on the object? (1 lb = 0. 454 kg) • Remember, it says NET force! There is a downward force based on the force of gravity (9. 8 m/s 2) • Fdown = mg = (0. 454 kg)(-9. 8 m/s 2) = -4. 5 N

More Force Problems • The instruments attached to a weather balloon have a mass of 5. 0 kg. The balloon is released and exerts an upward force of 98 N on the instruments. What is the acceleration of the balloon and the instruments?

More Force Problems • The instruments attached to a weather balloon have a mass of 5. 0 kg. The balloon is released and exerts an upward force of 98 N on the instruments. What is the acceleration of the balloon and the instruments? – Remember, the upward force has to overcome the force of gravity to accelerate upward F = ma + 49 N = (5. 0 kg)a a = 9. 8 m/s 2 up Downward force from gravity

Force Problem • A 873 -kg (1930 -lb) dragster, starting from rest, attains a speed of 26. 3 m/s (58. 9 mph) in 0. 59 s. What is the magnitude of the average net force on the dragster during this time?

Force Problem • A 873 -kg (1930 -lb) dragster, starting from rest, attains a speed of 26. 3 m/s (58. 9 mph) in 0. 59 s. What is the magnitude of the average net force on the dragster during this time? • A = Dv/Dt = (26. 3 m/s – 0) / 0. 59 s = 44. 58 m/s 2 • F = ma = (873 kg)(44. 58 m/s 2) = 3. 9 x 104 N

More Free Fall • Previously, we discussed the concept of free fall due to gravity – The acceleration due to gravity = 9. 8 m/s 2 – All objects in free fall have this acceleration when air resistance is neglected – This is because the force of the fall is proportional to its mass from the F= ma formula

Friction • Friction is a force and affects motion – Friction acts on materials that are in contact with each other – It always acts in a direct opposite to relative motion • When your car goes forward, the friction of the tires acts backwards! (Think vector diagram) – When two solid objects are in contact, friction occurs to due differences between the surfaces

Friction • Liquids and gases are fluids because they flow – We discussed this in chemistry! • Air resistance is the friction acting on something moving through the air – Previously, we’ve ignored air resistance completely

Friction • Think about when your car moves at a constant speed… – There is friction present between the tires and the road – The force applied (by the engine) balances the force of friction against the road – Is there net force here? – Is there acceleration?

Friction • Think about when your car moves at a constant speed… – The force applied (by the engine) balances the force of friction against the road – Is there net force here? • No! Force applied (engine) = friction force (road-tires) – Is there acceleration? • F = ma • If force equals zero, then acceleration = 0 (unless you have a magical car with no mass)

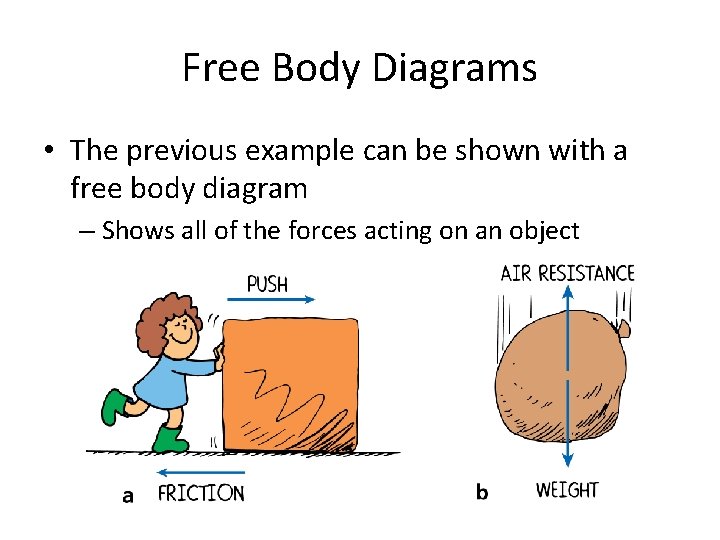
Free Body Diagrams • The previous example can be shown with a free body diagram – Shows all of the forces acting on an object

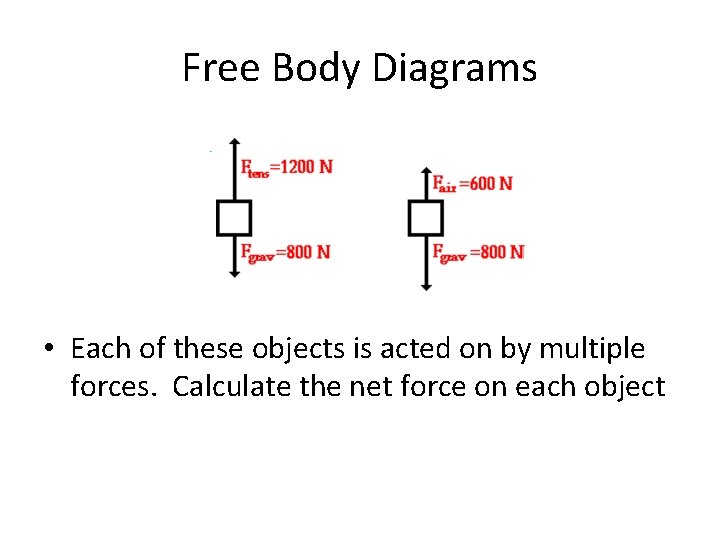
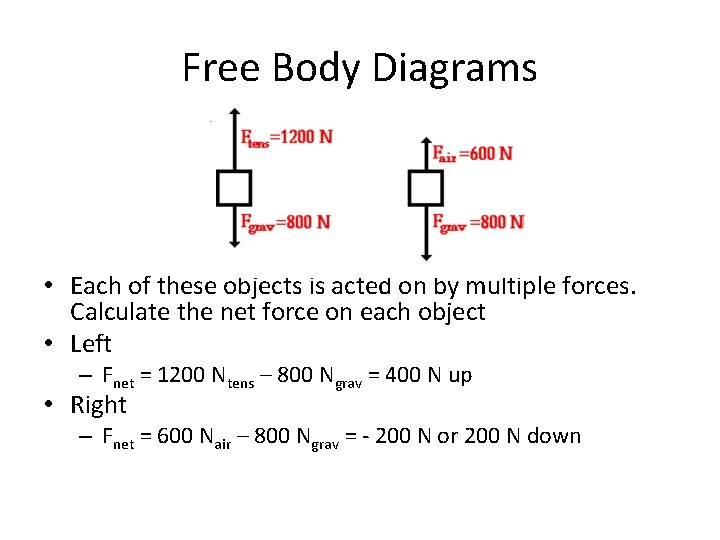
Free Body Diagrams • Each of these objects is acted on by multiple forces. Calculate the net force on each object

Free Body Diagrams • Each of these objects is acted on by multiple forces. Calculate the net force on each object • Left – Fnet = 1200 Ntens – 800 Ngrav = 400 N up • Right – Fnet = 600 Nair – 800 Ngrav = - 200 N or 200 N down

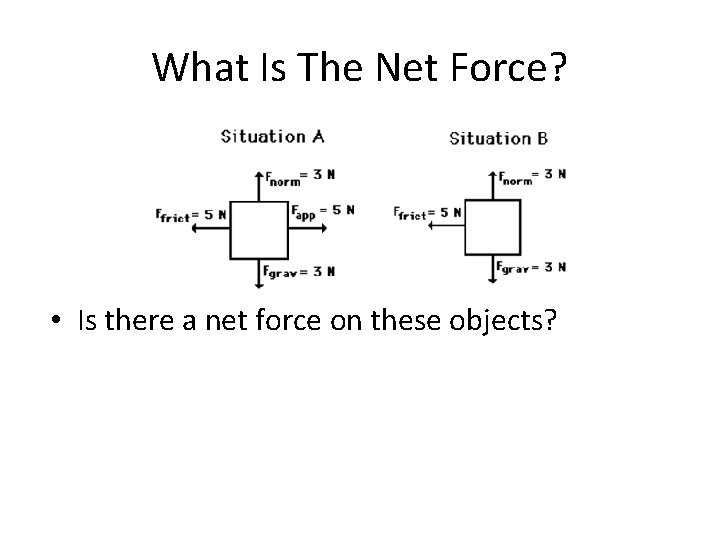
What Is The Net Force? • Is there a net force on these objects?

What Is The Net Force? • Is there a net force on these objects? – Situation A • Fnet = Ffriction – Fapp = 5 N left – 5 N right = 0 N • Fnet = Fnorm – Fgrav = 3 N up – 3 N down = 0 N – Situation B • Fnet = Ffriction – Fapp = 5 N left – 0 N right = 5 N left • Fnet = Fnorm – Fgrav = 3 N up – 3 N down = 0 N

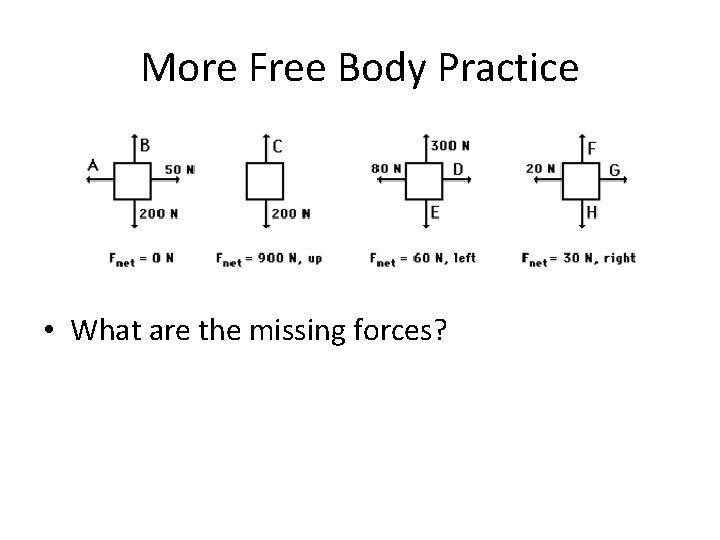
More Free Body Practice • What are the missing forces?

More Free Body Practice • What are the missing forces? – – – – A = 50 N left (balances right) B = 200 N up (balances left) C = 1100 N up (1100 N – 200 N = 900 N) D = 20 N right (80 N – 20 N = 60 N) E = 300 N down (balances up/down) F = H = doesn’t really matter G = 50 N right (50 N right – 20 N left = 30 N right)

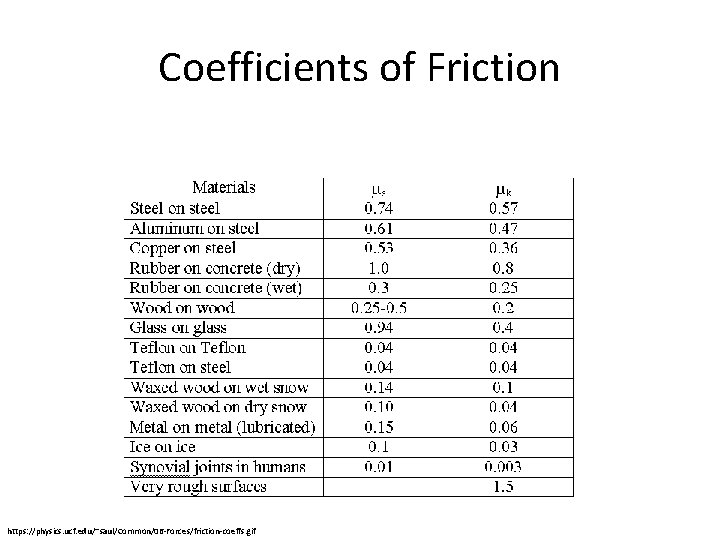
Back To Friction • Friction force can be calculated – Ffrict = µ • Fnorm – µ = coefficient of friction between surfaces • These are constants and must be given – Fnorm = Force applied in a given direction

Types Of Friction • Kinetic Friction – Exerted on one surface by another when the two surfaces rub against each other because one or both of them are moving • Static Friction – Exerted on one surface by another when there is no motion between the two surfaces • You must overcome the static friction force to get an object moving

Coefficients of Friction https: //physics. ucf. edu/~saul/Common/06 -Forces/friction-coeffs. gif

Friction Examples • If you use a horizontal force of 30. 0 N to slide a 12. 0 kg wooden crate across a floor at a constant velocity, what is the coefficient of friction between the crate and the floor?

Friction Examples • If you use a horizontal force of 30. 0 N to slide a 12. 0 kg wooden crate across a floor at a constant velocity, what is the coefficient of friction between the crate and the floor? • • Ffrict = µ • Fnorm Remember, Fnorm = ma, 30. 0 N = µ • (12. 0 kg)(9. 8 m/s 2) µ = 0. 26

Friction Examples • A block weighing 200 N is pushed along a surface. If it takes 80 N to get the block moving and 40 N to keep the block moving at a constant velocity, what are the coefficients of friction μs and μk?

Friction Examples • A block weighing 200 N is pushed along a surface. If it takes 80 N to get the block moving and 40 N to keep the block moving at a constant velocity, what are the coefficients of friction μs and μk? • Ffrict = µs • Fnorm • 80 N = µs x 200 N µs = 0. 4 • Ffrict = µk • Fnorm – 40 N = µs x 200 N µs = 0. 2

Air Resistance • A feather and a baseball fall with equal acceleration in a vacuum (no air), but unequally in the atmosphere • The force of air resistance lowers the net force acting on the falling objects – But it lowers the net force of the feather a whole lot more!!! • This is a type of friction!

Air Resistance • Speed and Area – The amount of air resistance is based on the speed an object is moving and the surface area the of object • Air resistance force ~ speed × frontal area https: //image. slidesharecdn. com/gravity-100810205111 -phpapp 02/95/gravity-13 -728. jpg? cb=1281473531

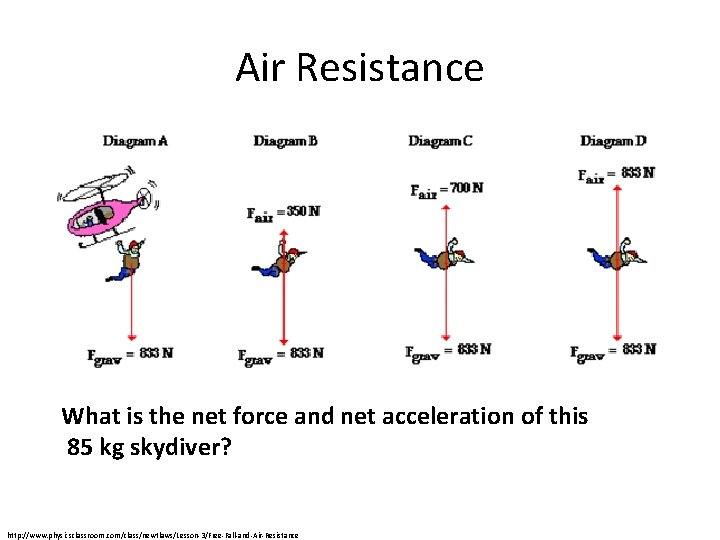
Air Resistance What is the net force and net acceleration of this 85 kg skydiver? http: //www. physicsclassroom. com/class/newtlaws/Lesson-3/Free-Fall-and-Air-Resistance

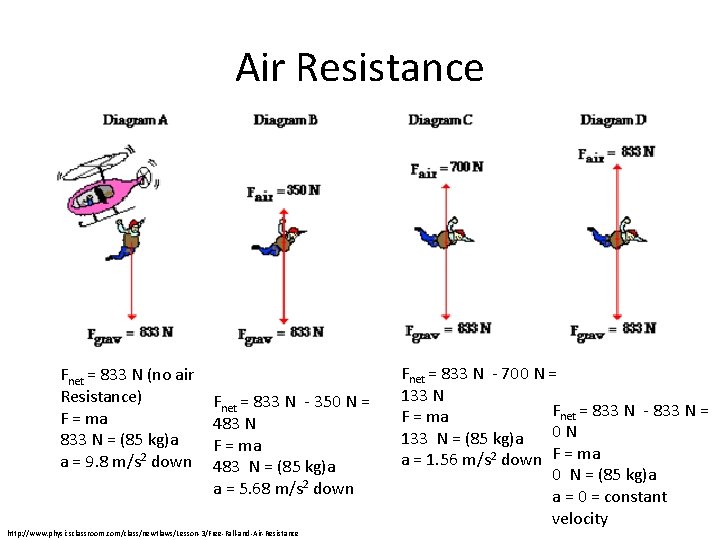
Air Resistance Fnet = 833 N (no air Resistance) F = ma 833 N = (85 kg)a a = 9. 8 m/s 2 down Fnet = 833 N - 350 N = 483 N F = ma 483 N = (85 kg)a a = 5. 68 m/s 2 down http: //www. physicsclassroom. com/class/newtlaws/Lesson-3/Free-Fall-and-Air-Resistance Fnet = 833 N - 700 N = 133 N Fnet = 833 N - 833 N = F = ma 0 N 133 N = (85 kg)a a = 1. 56 m/s 2 down F = ma 0 N = (85 kg)a a = 0 = constant velocity

Terminal Velocity • Terminal speed is the speed at which the acceleration of a falling object is zero because friction balances the weight • Terminal velocity is terminal speed together with the direction of motion – It’s not going to kill you – Your speed maxes out in free fall – Can be different based on mass and shape of falling object – Last skydiver in previous slide is falling at terminal velocity

Newton’s Third Law • Interaction Forces – Newton’s Third Law of Motion • “When an Object Exerts a Force On a Second Object, That Second Object Exerts an Equal and Opposite Force On the First Object. ”

Newton’s Third Law A hammer exerts a force on the nail and drives it into a board. • There must also be a force exerted on the hammer to halt it in the process. • Newton reasoned that while the hammer exerts a force on the nail, the nail exerts a force on the hammer. • In the interaction, there a pair of forces, one acting on the nail and the other acting on the hammer.

Newton’s Third Law • Concept of equilibrium – No net force in any direction – All forces canceled by other forces • Interaction Pair – There must be two forces, otherwise they couldn’t cancel!

Interaction Pairs In every interaction, the forces always occur in pairs. • You push against the floor, and the floor simultaneously pushes against you. • The tires of a car interact with the road to produce the car’s motion. The tires push against the road, and the road simultaneously pushes back on the tires. • When swimming, you push the water backward, and the water pushes you forward.

Interaction Pairs The interactions in the previous examples depend on friction. A person trying to walk on ice, where friction is minimal, may not be able to exert an action force against the ice. Without the action force (friction) there cannot be a reaction force, and thus there is no resulting forward motion.

Interaction Pairs • A tug of war occurs between boys and girls on a polished floor that’s somewhat slippery. If the boys are wearing socks and the girls are wearing rubber-soled shoes, who will surely win, and why?

Interaction Pairs • A tug of war occurs between boys and girls on a polished floor that’s somewhat slippery. If the boys are wearing socks and the girls are wearing rubber-soled shoes, who will surely win, and why? – The girls will win. The force of friction is greater between the girls’ feet and the floor than between the boys’ feet and the floor. When both the girls and the boys exert action forces on the floor, the floor exerts a greater reaction force on the girls’ feet. The girls stay at rest and the boys slide toward the girls.