Newtons Law of Motion in Software Development Processes

Newton's Law of Motion in Software Development Processes? CS 690 S Computer Science Seminar Aditya P. Mathur (CS) in collaboration with … João Cangussu (CS) Ray. A. De. Carlo (ECE) Monday November 5, 2001 Software Process Control 1

Research Question Can we control the Software Development Process in a manner similar to how physical systems and processes are controlled ? The fundamental control problem (Ref: Control System Design by G. C. Goodwin et al. , Prentice Hall, 2001) The central problem in control is to find a technically feasible way to act on a given process so that the process adheres, as closely as possible to some desired behavior. Furthermore, this approximate behavior should be achieved in the face of uncertainty of the process and in the presence of uncontrollable external disturbances acting on the process. Software Process Control 2

Research Methodology [1] 1. Understand how physical systems are controlled? 2. Understand how software systems relate to physical systems. Are there similarities? Are there differences? 3. Understand theory and practice of the control of physical systems. 4. Can we borrow from this theory? If “yes, ” then proceed further, else drink coffee or tea and think of another research direction. 5. Adapt control theory to the control of SDP and develop models and methods to control the SDP. 6. Study the behavior of the models and methods in real-life settings. Software Process Control 3

Research Methodology [2] 7. Improve the model and methods. 8. Repeat steps 6 and 7 until you are thoroughly bored or get rich. Software Process Control 4

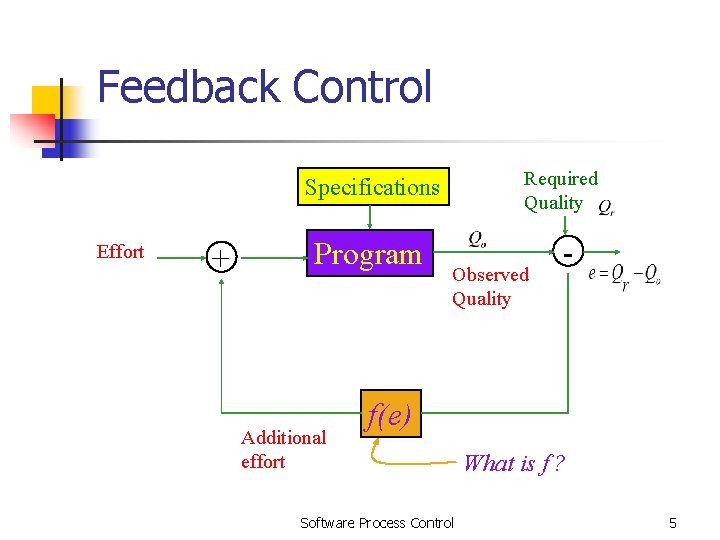
Feedback Control Required Quality Specifications Effort + Program Additional effort Observed Quality - f(e) Software Process Control What is f ? 5

Software Development Process: Definitions A Software Development Process (SDP) is a sequence of well defined activities used in the production of software. An SDP usually consists of several sub-processes that may or may not operate in a sequence. The Design Process, the Software Test Process, and the Configuration Management Process are examples of sub-processes of the SDP. Software Process Control 6

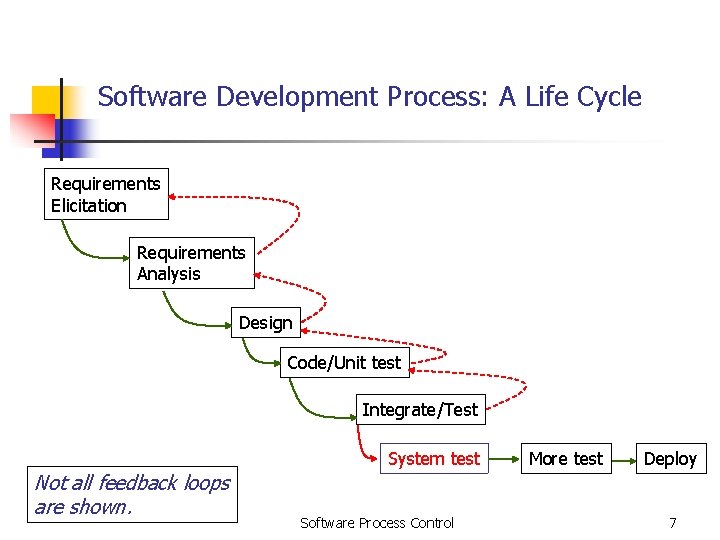
Software Development Process: A Life Cycle Requirements Elicitation Requirements Analysis Design Code/Unit test Integrate/Test System test Not all feedback loops are shown. Software Process Control More test Deploy 7

Current Focus Software Test Process (STP): System test phase Objective: Control the STP so that the quality of the tested software is as desired. Quantification of quality of software: • Number of remaining errors • Reliability Software Process Control 8

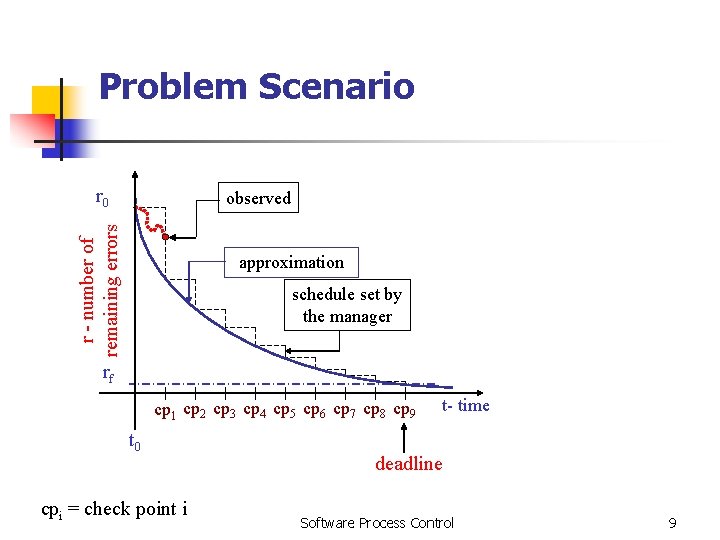
Problem Scenario r 0 r - number of remaining errors observed approximation schedule set by the manager rf cp 1 cp 2 cp 3 cp 4 cp 5 cp 6 cp 7 cp 8 cp 9 t 0 cpi = check point i t- time deadline Software Process Control 9

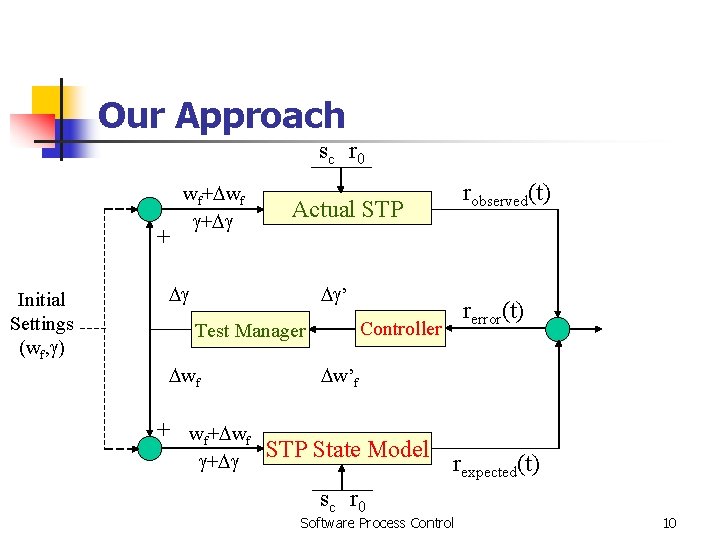
Our Approach s c r 0 + Initial Settings (wf, ) wf+ wf + robserved(t) Actual STP ’ Controller Test Manager wf + rerror(t) w’f STP State Model s c r 0 rexpected(t) Software Process Control 10

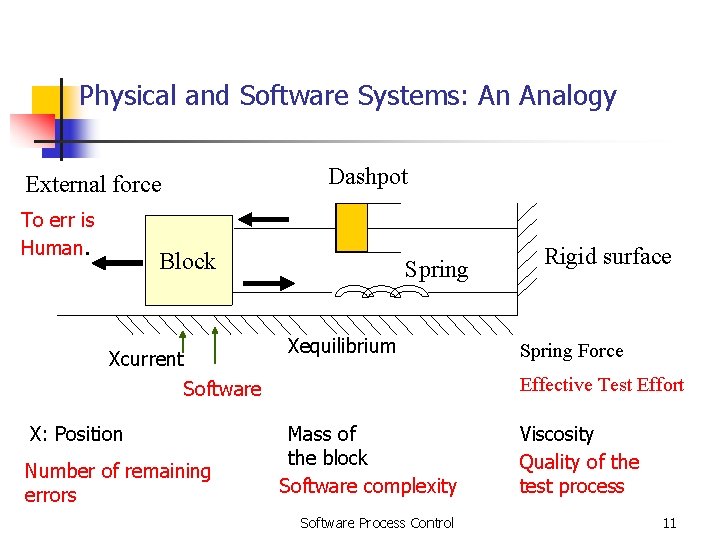
Physical and Software Systems: An Analogy Dashpot External force To err is Human. Block Xcurrent Spring Xequilibrium Number of remaining errors Spring Force Effective Test Effort Software X: Position Rigid surface Mass of the block Software complexity Software Process Control Viscosity Quality of the test process 11

Physical Systems: Controllability Is it possible to control X (r) by adjusting Y (workforce and process quality)? Observability Does the system have distinct states that cannot be unambiguously identified by the controller ? Robustness Will control be regained satisfactorily after an unexpected disturbance? Software Process Control 12

Physical Systems: Laws of Motion [1] First Law: Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it. Does not apply to testing because the number of errors does not change when no external effort is applied to the application. Software Process Control 13

Physical Systems: Laws of Motion [2] Newton’s Second Law: The relationship between an object's mass m, its acceleration a, and the applied force F is F = ma. CDM’s First Law: The relationship between an complexity Sc of an applications, its rate of reduction in the number of. . remaining errors, and the applied effort E is E=Sc r. Software Process Control 14

Physical Systems: Laws of Motion [3] Third Law: For every action force, there is an equal and opposite reaction force. When an effort is applied to test software, it leads to fatigue on the tester. This is not a scientific relationship. Software Process Control 15

Assumption I: CDM’s First Law The magnitude of the rate of decrease of the remaining errors is directly proportional to the net applied effort and inversely proportional to the complexity of the program under test. This is derived from Newton’s Second Law of motion. Software Process Control 16

Assumption II: CDM’s Second Law Analogy with the spring: The magnitude of the effective test effort is proportional to the product of the applied work force and number of remaining errors. for an appropriate . Software Process Control 17

Assumption III: CDM’s Third Law Analogy with the dashpot: The error reduction resistance is proportional to the error reduction velocity and inversely proportional to the overall quality of the test phase. for an appropriate . Software Process Control 18

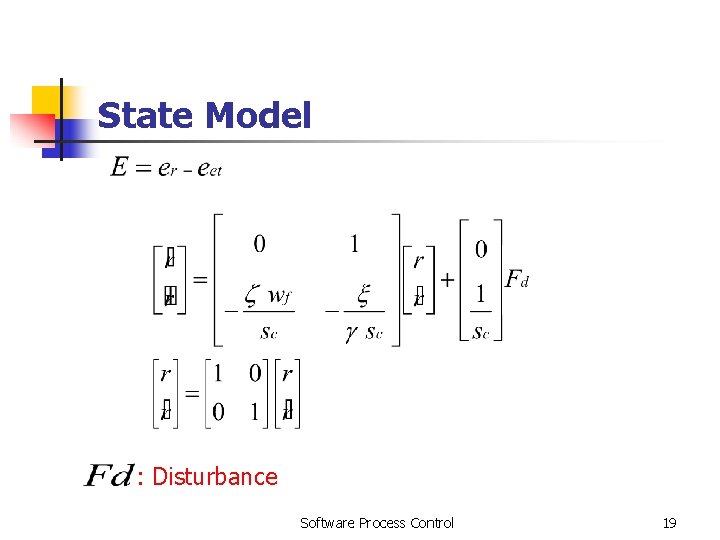
State Model : Disturbance Software Process Control 19

Computing the feedback Software Process Control 20

Case Study II: Razorfish Project Description Project Goal: translate 4 million lines of Cobol code to SAP/R 3 A tool has been developed to achieve the goal of this project. Goal of the test process: (a) Test the generated code, not the tool. (b) Reduce the number of errors by about 85%. Software Process Control 21

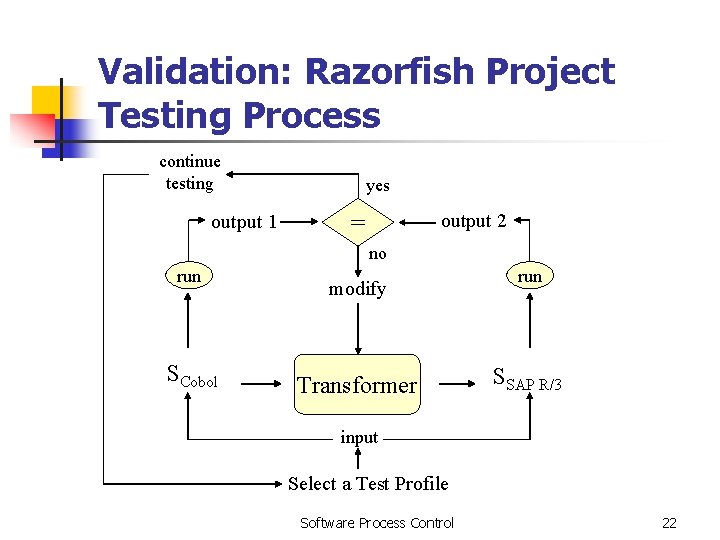
Validation: Razorfish Project Testing Process continue testing output 1 yes = output 2 no run SCobol modify Transformer run SSAP R/3 input Select a Test Profile Software Process Control 22

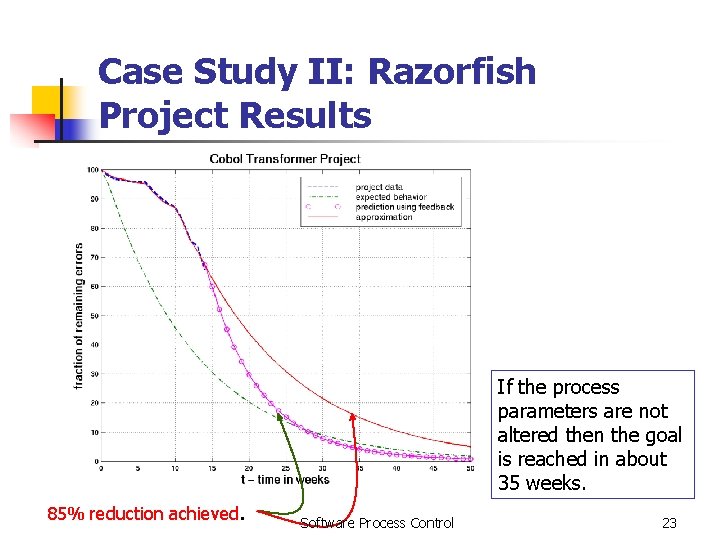
Case Study II: Razorfish Project Results If the process parameters are not altered then the goal is reached in about 35 weeks. 85% reduction achieved. Software Process Control 23

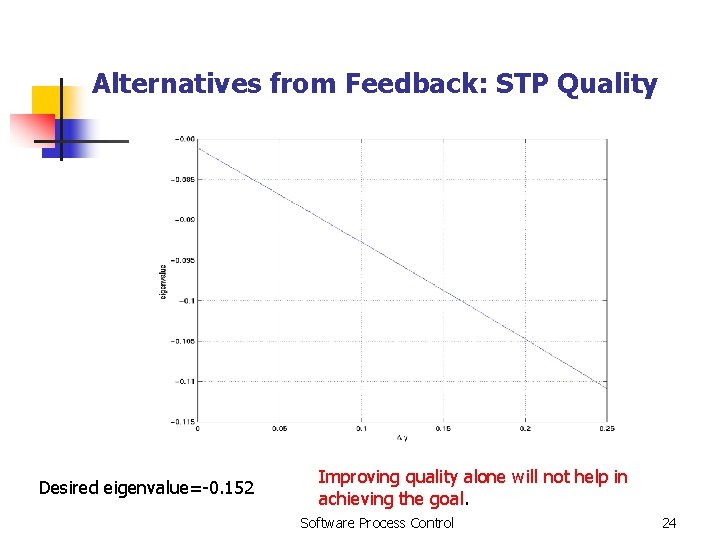
Alternatives from Feedback: STP Quality Desired eigenvalue=-0. 152 Improving quality alone will not help in achieving the goal. Software Process Control 24

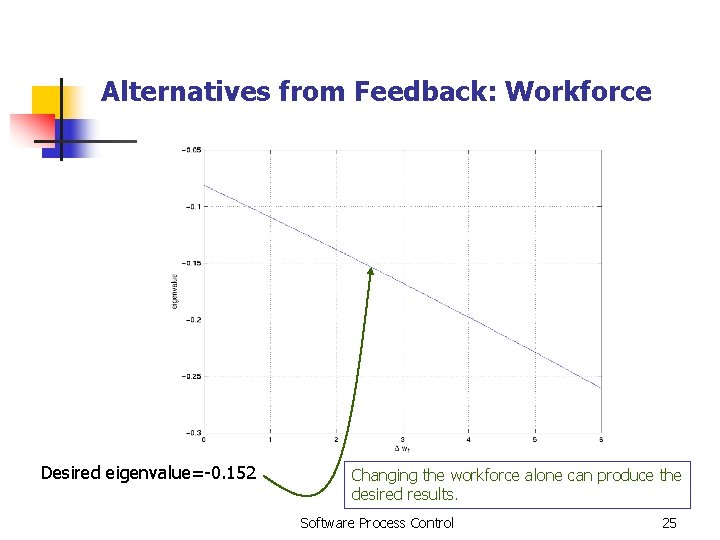
Alternatives from Feedback: Workforce Desired eigenvalue=-0. 152 Changing the workforce alone can produce the desired results. Software Process Control 25

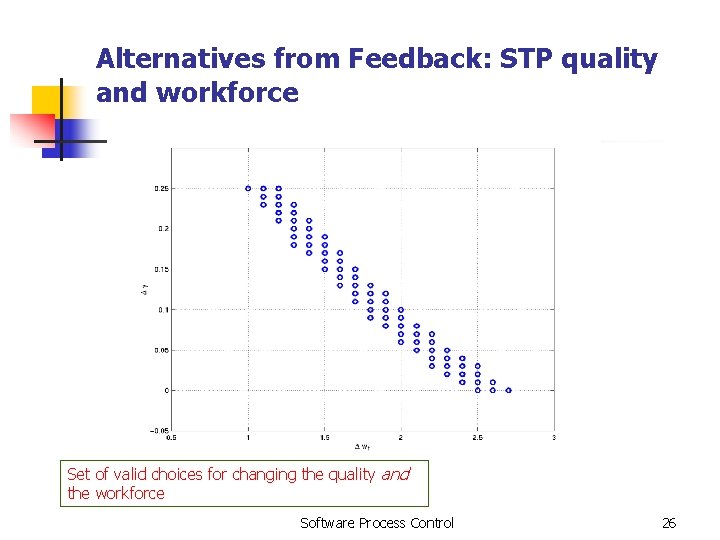
Alternatives from Feedback: STP quality and workforce Set of valid choices for changing the quality and the workforce Software Process Control 26

Summary Analogy between physical and software systems presented. The notion of feedback control of software processes introduced. One case study described. Parameter estimation techniques used for model calibration. Made use of system identification techniques. Software Process Control 27

Ongoing Research Sensitivity analysis: r is more sensitive to changes in the model parameters during the early stages of the test process than during the later stages. An improvement in the quality of the STP is more effective than an increase in the workforce. Brook’s Law was also observed during the analysis. Expansion of the model to include the entire SDP. Additional case studies. Software Process Control 28