Newtons Divided Difference Polynomial Method of Interpolation Major

Newton’s Divided Difference Polynomial Method of Interpolation Major: All Engineering Majors Authors: Autar Kaw, Jai Paul http: //numericalmethods. eng. usf. edu Numerical Methods for STEM undergraduates http: //numericalmethods. eng. usf. edu 1

What is Interpolation ? Given (x 0, y 0), (x 1, y 1), …… (xn, yn), find the value of ‘y’ at a value of ‘x’ that is not given. 2 lmethods. eng. usf. edu ht

Interpolants Polynomials are the most common choice of interpolants because they are easy to: Evaluate Differentiate, and Integrate. 3 lmethods. eng. usf. edu ht

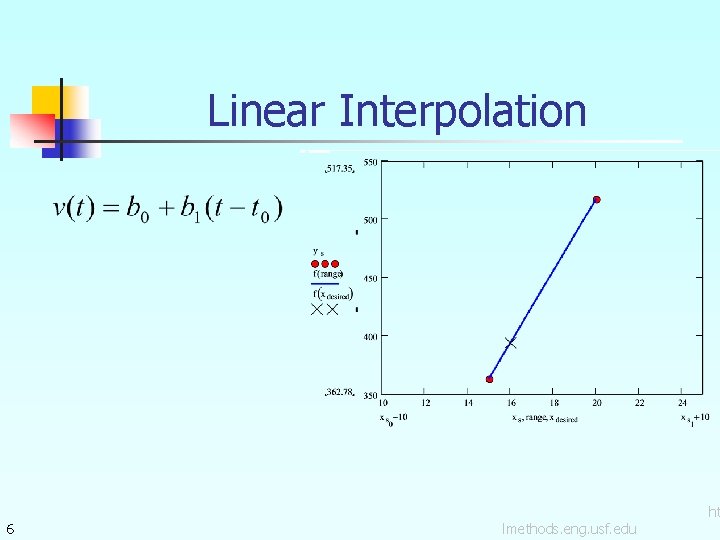
Newton’s Divided Difference Method Linear interpolation: Given linear interpolant through the data pass a where 4 lmethods. eng. usf. edu ht

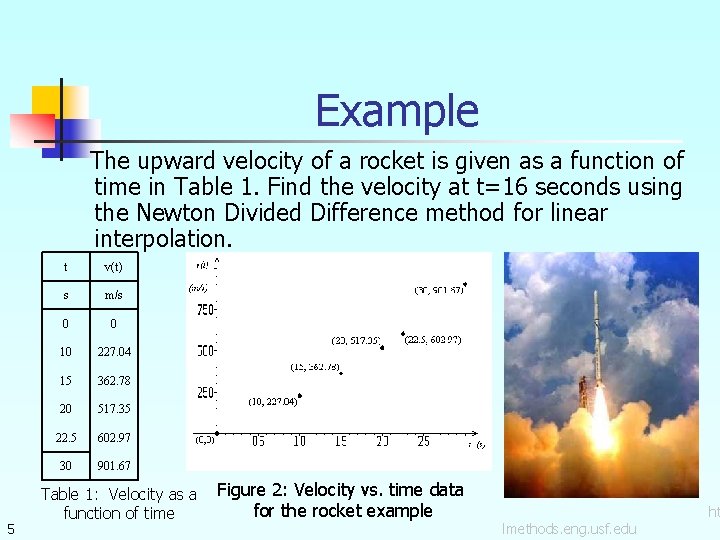
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Newton Divided Difference method for linear interpolation. 5 t v(t) s m/s 0 0 10 227. 04 15 362. 78 20 517. 35 22. 5 602. 97 30 901. 67 Table 1: Velocity as a function of time Figure 2: Velocity vs. time data for the rocket example lmethods. eng. usf. edu ht

Linear Interpolation 6 lmethods. eng. usf. edu ht

Linear Interpolation (contd) 7 lmethods. eng. usf. edu ht

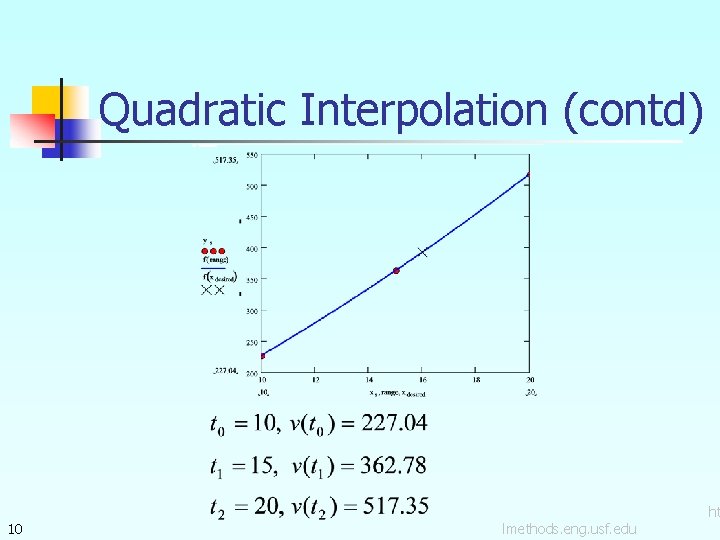
Quadratic Interpolation 8 lmethods. eng. usf. edu ht

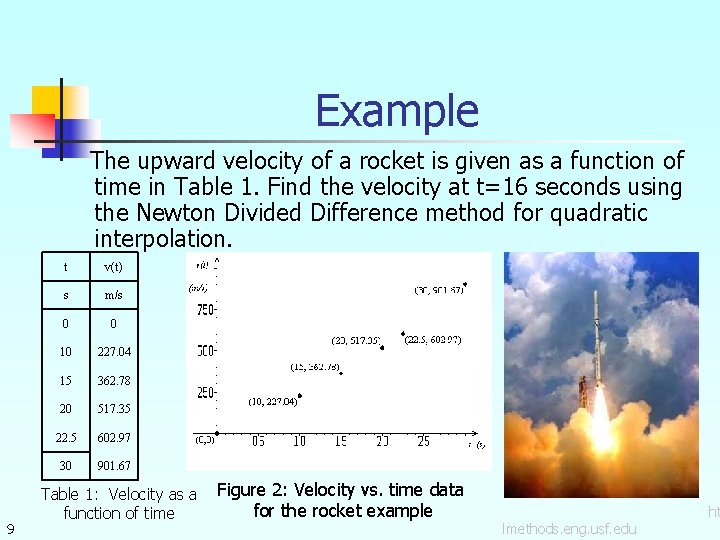
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Newton Divided Difference method for quadratic interpolation. 9 t v(t) s m/s 0 0 10 227. 04 15 362. 78 20 517. 35 22. 5 602. 97 30 901. 67 Table 1: Velocity as a function of time Figure 2: Velocity vs. time data for the rocket example lmethods. eng. usf. edu ht

Quadratic Interpolation (contd) 10 lmethods. eng. usf. edu ht

Quadratic Interpolation (contd) 11 lmethods. eng. usf. edu ht

Quadratic Interpolation (contd) 12 lmethods. eng. usf. edu ht

General Form where Rewriting 13 lmethods. eng. usf. edu ht

General Form 14 lmethods. eng. usf. edu ht

General form 15 lmethods. eng. usf. edu ht

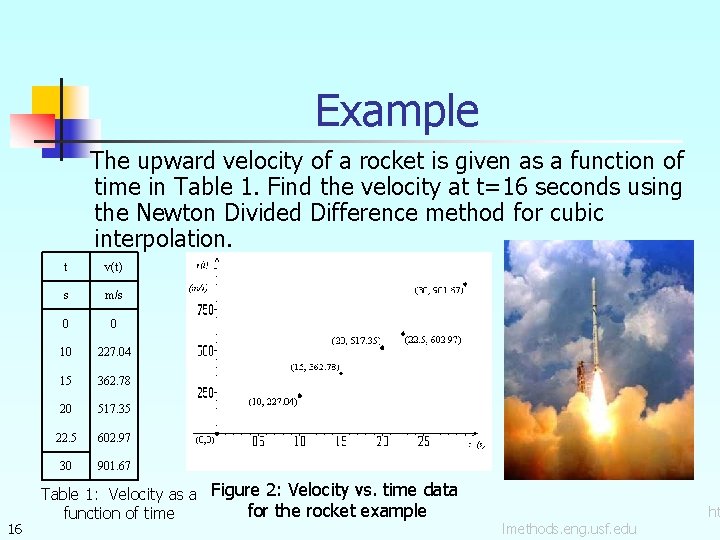
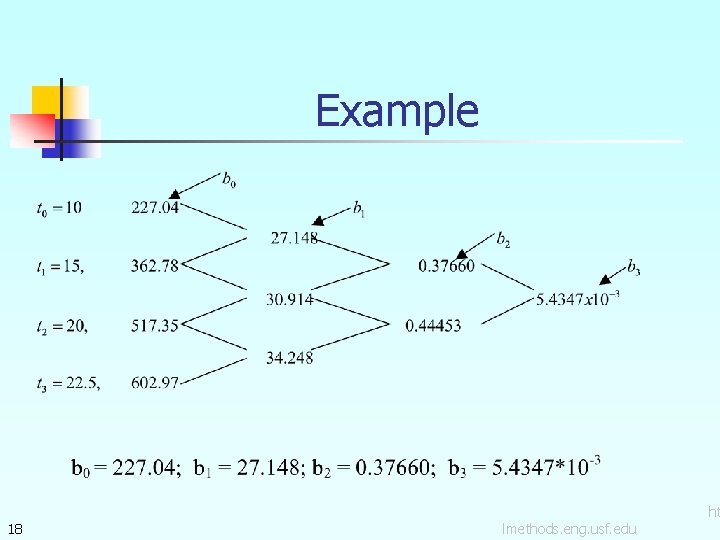
Example The upward velocity of a rocket is given as a function of time in Table 1. Find the velocity at t=16 seconds using the Newton Divided Difference method for cubic interpolation. 16 t v(t) s m/s 0 0 10 227. 04 15 362. 78 20 517. 35 22. 5 602. 97 30 901. 67 Table 1: Velocity as a Figure 2: Velocity vs. time data for the rocket example function of time lmethods. eng. usf. edu ht

Example The velocity profile is chosen as we need to choose four data points that are closest to 17 lmethods. eng. usf. edu ht

Example 18 lmethods. eng. usf. edu ht

Example 19 lmethods. eng. usf. edu ht

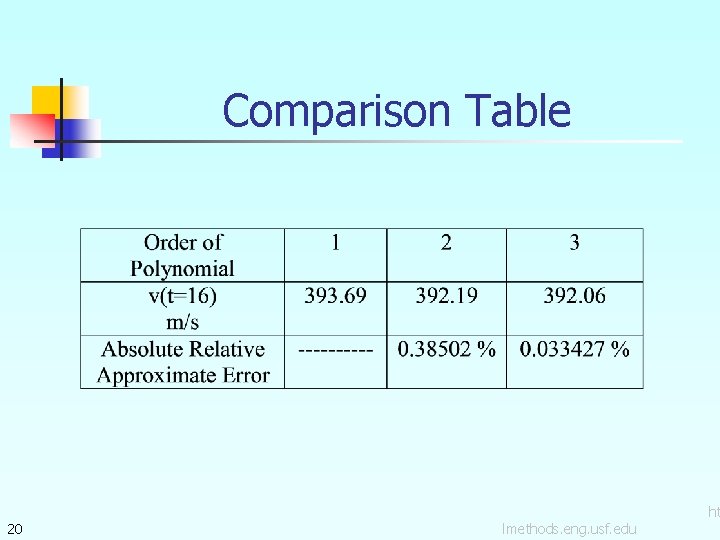
Comparison Table 20 lmethods. eng. usf. edu ht

Distance from Velocity Profile Find the distance covered by the rocket from t=11 s to t=16 s ? 21 lmethods. eng. usf. edu ht

Acceleration from Velocity Profile Find the acceleration of the rocket at t=16 s given that 22 lmethods. eng. usf. edu ht