Newtons Divided Difference Polynomial Method of Interpolation Civil

Newton’s Divided Difference Polynomial Method of Interpolation Civil Engineering Majors Authors: Autar Kaw, Jai Paul http: //numericalmethods. eng. usf. edu Transforming Numerical Methods Education for STEM Undergraduates http: //numericalmethods. eng. usf. edu 1

Newton’s Divided Difference Method of Interpolation http: //numericalmethods. eng. usf. edu

What is Interpolation ? Given (x 0, y 0), (x 1, y 1), …… (xn, yn), find the value of ‘y’ at a value of ‘x’ that is not given. 3 lmethods. eng. usf. edu http: //numerica

Interpolants Polynomials are the most common choice of interpolants because they are easy to: Evaluate Differentiate, and Integrate. 4 lmethods. eng. usf. edu http: //numerica

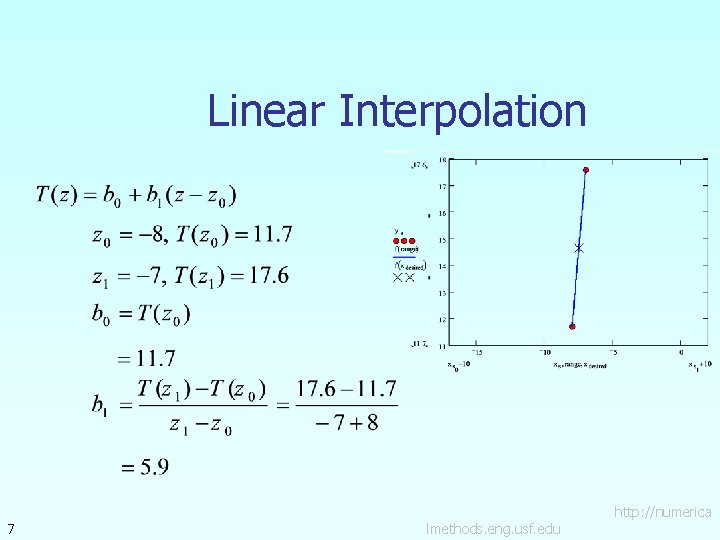
Newton’s Divided Difference Method Linear interpolation: Given linear interpolant through the data pass a where 5 lmethods. eng. usf. edu http: //numerica

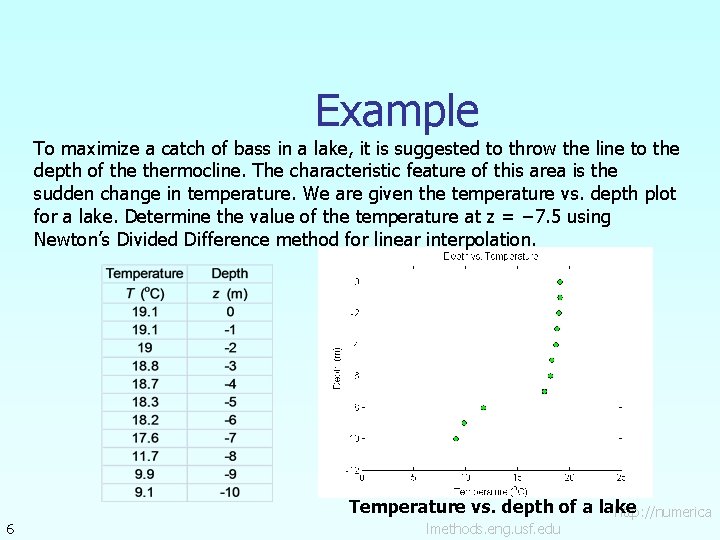
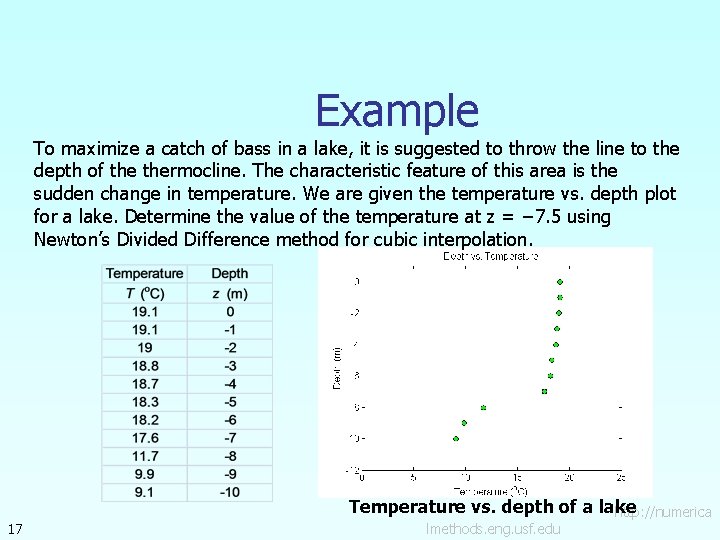
Example To maximize a catch of bass in a lake, it is suggested to throw the line to the depth of thermocline. The characteristic feature of this area is the sudden change in temperature. We are given the temperature vs. depth plot for a lake. Determine the value of the temperature at z = − 7. 5 using Newton’s Divided Difference method for linear interpolation. 6 Temperature vs. depth of a lake http: //numerica lmethods. eng. usf. edu

Linear Interpolation 7 lmethods. eng. usf. edu http: //numerica

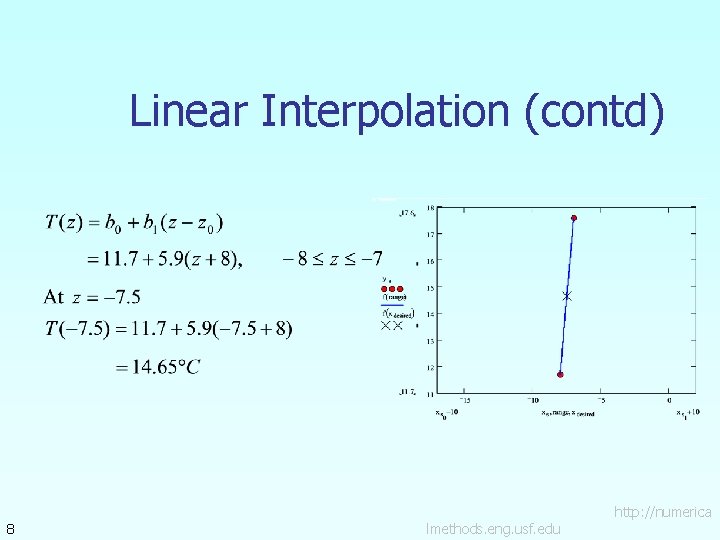
Linear Interpolation (contd) 8 lmethods. eng. usf. edu http: //numerica

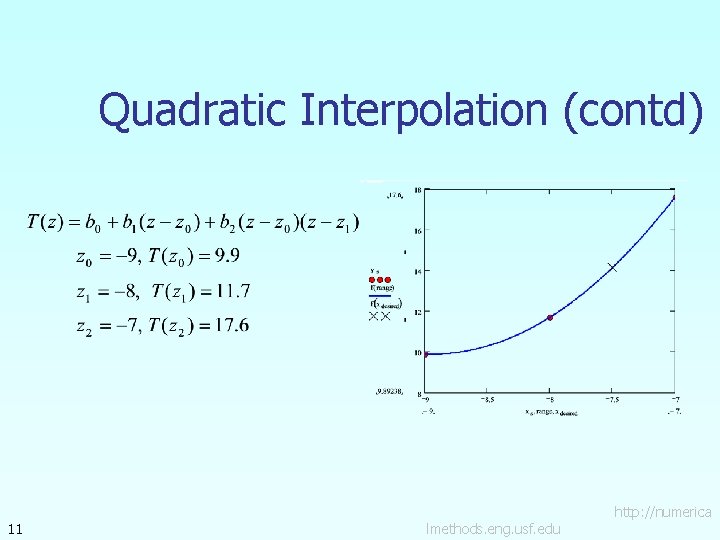
Quadratic Interpolation 9 lmethods. eng. usf. edu http: //numerica

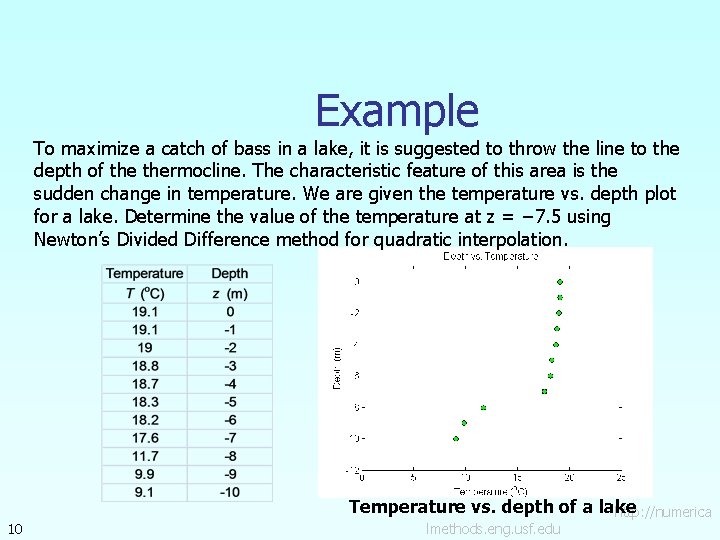
Example To maximize a catch of bass in a lake, it is suggested to throw the line to the depth of thermocline. The characteristic feature of this area is the sudden change in temperature. We are given the temperature vs. depth plot for a lake. Determine the value of the temperature at z = − 7. 5 using Newton’s Divided Difference method for quadratic interpolation. 10 Temperature vs. depth of a lake http: //numerica lmethods. eng. usf. edu

Quadratic Interpolation (contd) 11 lmethods. eng. usf. edu http: //numerica

Quadratic Interpolation (contd) 12 lmethods. eng. usf. edu http: //numerica

Quadratic Interpolation (contd) 13 lmethods. eng. usf. edu http: //numerica

General Form where Rewriting 14 lmethods. eng. usf. edu http: //numerica

General Form 15 lmethods. eng. usf. edu http: //numerica

General form 16 lmethods. eng. usf. edu http: //numerica

Example To maximize a catch of bass in a lake, it is suggested to throw the line to the depth of thermocline. The characteristic feature of this area is the sudden change in temperature. We are given the temperature vs. depth plot for a lake. Determine the value of the temperature at z = − 7. 5 using Newton’s Divided Difference method for cubic interpolation. 17 Temperature vs. depth of a lake http: //numerica lmethods. eng. usf. edu

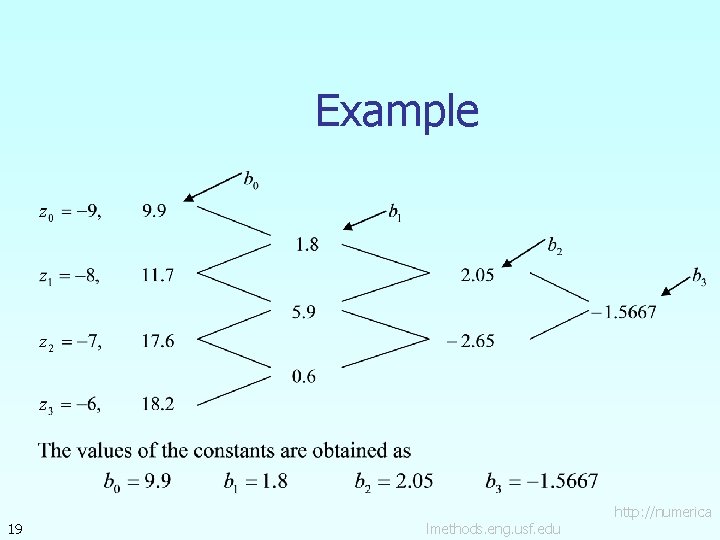
Example 18 lmethods. eng. usf. edu http: //numerica

Example 19 lmethods. eng. usf. edu http: //numerica

Example 20 lmethods. eng. usf. edu http: //numerica

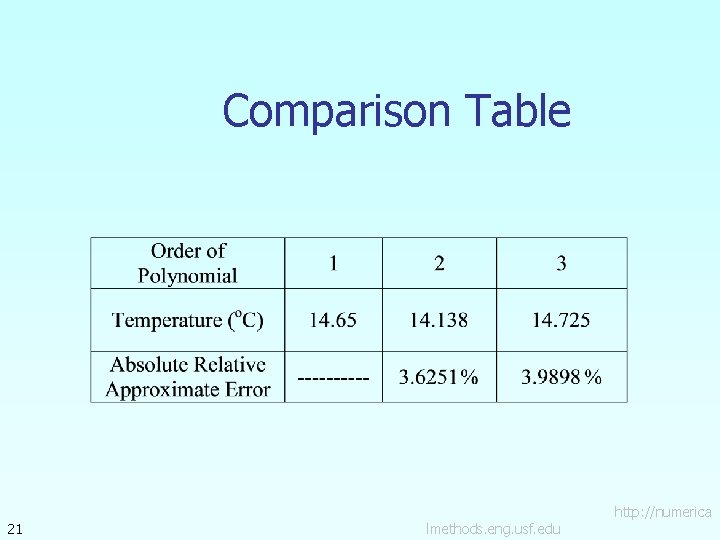
Comparison Table 21 lmethods. eng. usf. edu http: //numerica

Thermocline What is the value of depth at which thermocline exists? The position where thermocline exists is given where . 22 lmethods. eng. usf. edu http: //numerica

Additional Resources For all resources on this topic such as digital audiovisual lectures, primers, textbook chapters, multiple-choice tests, worksheets in MATLAB, MATHEMATICA, Math. Cad and MAPLE, blogs, related physical problems, please visit http: //numericalmethods. eng. usf. edu/topics/newton_div ided_difference_method. html

THE END http: //numericalmethods. eng. usf. edu