Newtonian Mechanics Kinematics Kinematics Introduction A large part

Newtonian Mechanics Kinematics

Kinematics Introduction A large part of our everyday experiences, as well as our scientific experiences, concern things that move. For this reason, the study of motion is one of the most basic studies in physics. Kinematics describes the positions and motions of objects in space as a function of time but does not consider the causes of motion. The study of the causes of motion is called Dynamics.

Kinematics Introduction This unit is restricted to translational motion: Along a straight line horizontally vertically In a 2 -dimensional plane projectile motion circular motion

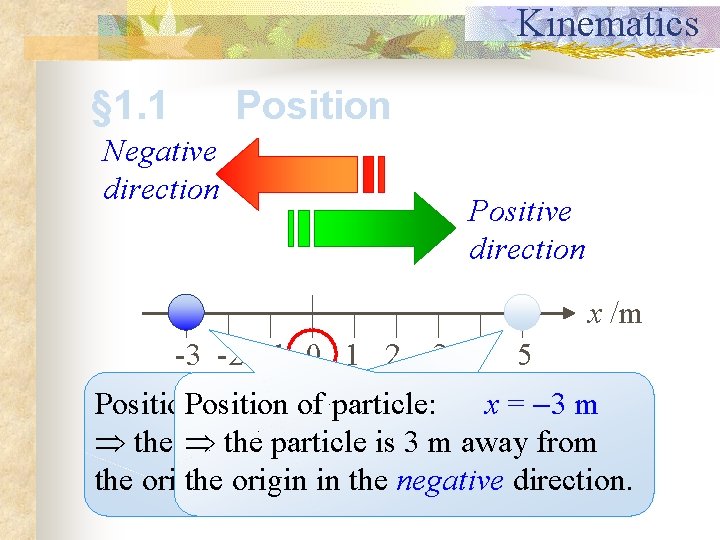
Kinematics § 1. 1 Position The motion of a particle is completely known if the particle’s position in space is known at all times. For one–dimensional motion, the location of a particle is its position relative to some reference point, often the origin (or zero point) of an axis.

Kinematics § 1. 1 Position Negative direction Positive direction x /m -3 -2 -1 0 1 2 3 4 5 Position of particle: x = 5 mx = 3 m the particle the Origin particle is 5 m away is 3 mfrom away from the origin the in origin the positive in the negative direction.

Kinematics § 1. 2 Displacement Definition It is a vector quantity. Displacement is defined as the linear distance of the position of an object from a reference point. The path taken Symbols: s, not matter, The sign gives x does (horizontal), only initial & the direction y as(vertical) final positions w. r. t. the origin. S. I. unit: metre (m) matter.

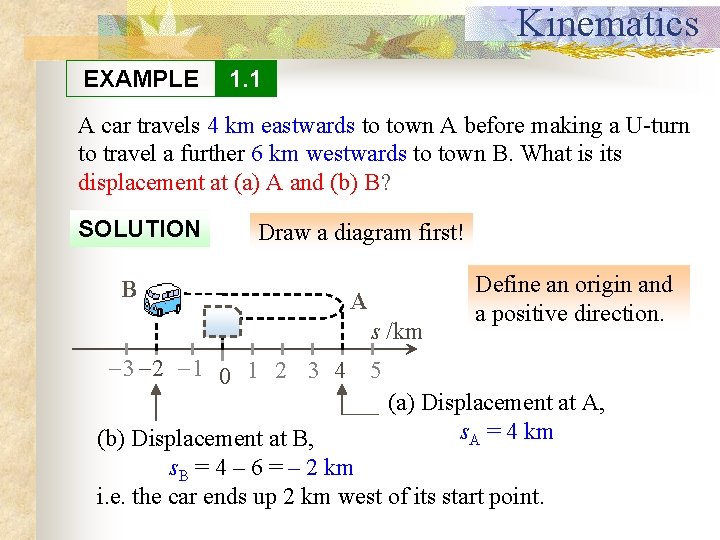
Kinematics EXAMPLE 1. 1 A car travels 4 km eastwards to town A before making a U-turn to travel a further 6 km westwards to town B. What is its displacement at (a) A and (b) B? SOLUTION Draw a diagram first! B A s /km 3 2 1 0 1 2 3 4 Define an origin and a positive direction. 5 (a) Displacement at A, s. A = 4 km (b) Displacement at B, s. B = 4 – 6 = – 2 km i. e. the car ends up 2 km west of its start point.

Kinematics § 1. 2 Distance S. I. unit: metre (m) Definition Symbols: d Distance is defined as the total length of the actual path covered by an object. It is a scalar quantity. Distance 0 once object moves, so distance displacement.

Kinematics EXAMPLE 1. 2 From eg 1. 1, the car now moves from B back to its start point. What is (a) its final displacement and (b) the total distance travelled since it started moving ? SOLUTION (a) Since the car ends up at its start point, final displacement = 0. (b) The car must travel another 2 km eastwards to return to its start point. Therefore total distance travelled = 4 + 6 + 2 = 12 km

Kinematics § 1. 3 Graphical Representation Instead of using diagrams, we can describe position with a graph of position as a function of time. EXAMPLE 1. 3 If a rabbit remains stationary at a distance of 2 m from its cage, its position time graph would be: x/m 2 1 0 1 2 3 4 t/s

Kinematics EXAMPLE 1. 4 If a moving car has a displacement s from O, what deductions can be made if its s t graph is (a) graph 1. 3. 1, or (b) graph 1. 3. 2? Sketch car’s 1. 3. 1 path s / m of. Graph SOLUTION for (a) & (b) 2 (b) Here, the car does notofundergo (a) Taking the right side O to 1 uniform motion. Atthe t = car 0 and t t/s t=0 be positive, we see = 3 s, moving its displacement notthe 0 1 2 3 4 t = 4 s starts from 1 mison changing. This the car is 1 s /m left side of O towards the 1 0 1 2 3 instantaneously at rest. s/m right. nd In thestraight 2 halfline of the journey, Graph 1. 3. 2 The 3 the car’s displacement falls displacement increases t 2= 5 s steadily to with zero time. at t = 5 s. This t=3 s uniformly 1 t = 0 the car has moved back to its t/s start point. 0 1 2 3 s /m 1 2 3 4 5

Kinematics § 2. 1 Average Speed Definition Average speed is defined as the total distance travelled over the total time taken, i. e. total distance travelled Average speed, <u> = time taken to travel the distance d = t

Kinematics § 2. 1 Average Velocity Definition Average velocity is defined as the total displacement over the total time taken, i. e. total displacement Average velocity, <v> = time taken for the displacement s = t

Kinematics § 2. 1 Average Speed & Velocity Average speed is a positive scalar, while velocity is a vector. d <u> = t Common symbols: u or v s <v> = t Both average speed and velocity have the same S. I. units of metres per second (m s 1).

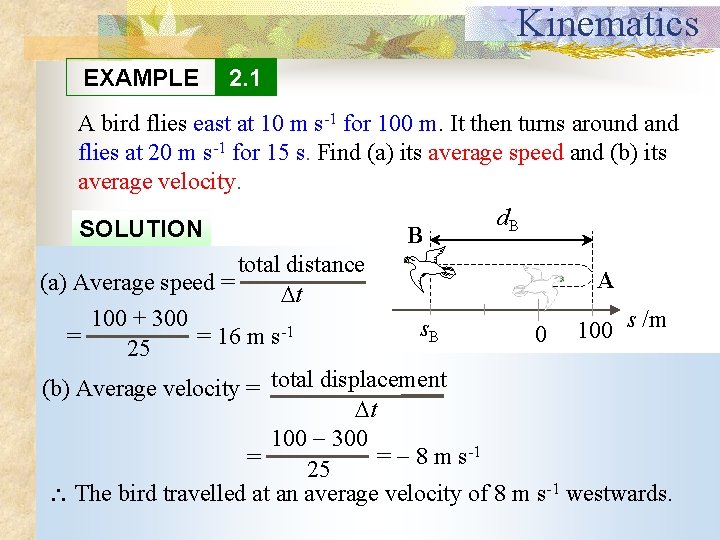
Kinematics EXAMPLE 2. 1 A bird flies east at 10 m s-1 for 100 m. It then turns around and flies at 20 m s-1 for 15 s. Find (a) its average speed and (b) its average velocity. d. B SOLUTION B total distance Time taken to reach A, A (a) Average speed = t d. A 100 t. A 100 = + 300 = 10 -1 s s /m = s 100 v B 0 = = 16 m s A 10 25 Given time from A to=B, total t. B =displacement 15 s, total time for the whole journey is (b) Average velocity t = t. A + t. B = 10 t+ 15 = 25 s 100 300 Distance travelled to=reach A, d. A ==100 8 m s-1 25 -1 westwards. Distance travelled from A average to B, d. B velocity = v. B t. Bof= 820 m s 15 = 300 m The bird travelled at an

Kinematics § 2. 2 Instantaneous Speed Same units & & Velocity Definition symbols as average velocity Instantaneous speed is velocity is defined as the definedinstantaneous as the magnitude of of change of rate the instantaneous velocity displacement with time, i. e. ds s lim Instantaneous velocity, v = = t→ 0 t dt We will use ‘velocity’ to mean ‘instantaneous velocity’.

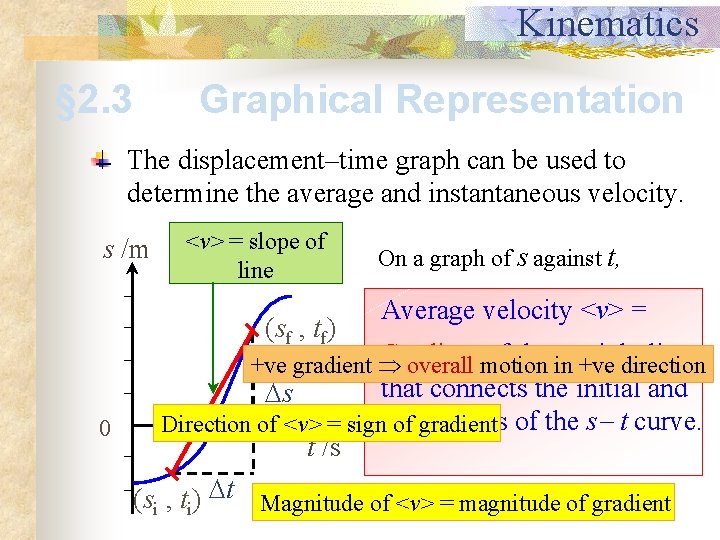
Kinematics § 2. 3 Graphical Representation The displacement–time graph can be used to determine the average and instantaneous velocity. <v> = slope of line s /m (sf , tf) On a graph of s against t, Average velocity <v> = Gradient of the in straight line +ve gradient overall motion +ve direction that connects the initial and points of the s t curve. Direction of <v> = signfinal of gradient 0 t /s (s , t ) t Magnitude of <v> = magnitude of gradient s i i

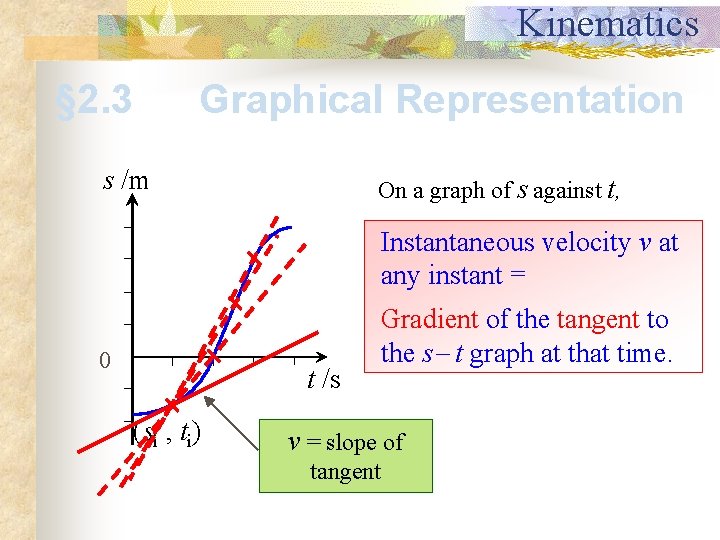
Kinematics § 2. 3 Graphical Representation s /m On a graph of s against t, Instantaneous velocity v at any instant = 0 t /s (si , ti) Gradient of the tangent to the s t graph at that time. v = slope of tangent

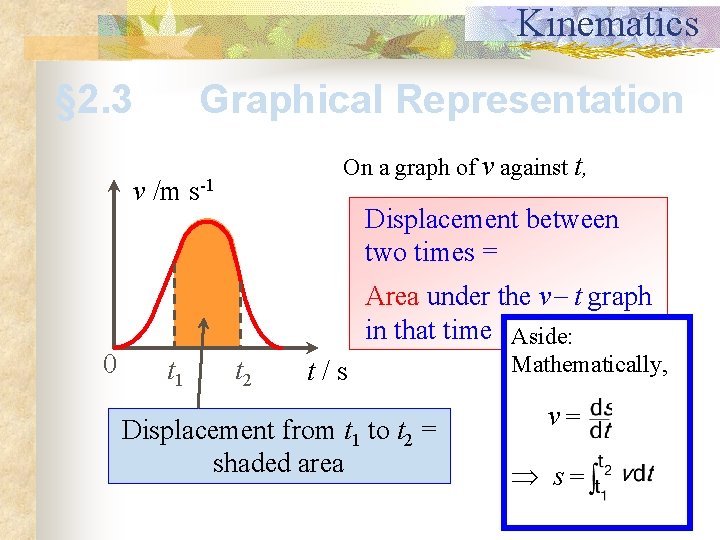
Kinematics § 2. 3 Graphical Representation On a graph of v against t, v /m s-1 0 Displacement between two times = Area under the v t graph in that time interval. Aside: t 1 t 2 t/s Displacement from t 1 to t 2 = shaded area Mathematically, v= s=

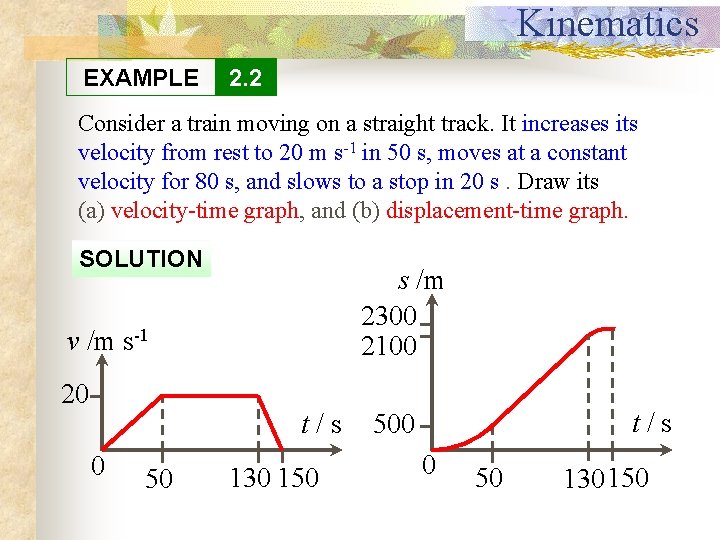
Kinematics EXAMPLE 2. 2 Consider a train moving on a straight track. It increases its velocity from rest to 20 m s-1 in 50 s, moves at a constant velocity for 80 s, and slows to a stop in 20 s. Draw its (a) velocity-time graph, and (b) displacement-time graph. SOLUTION v /m s-1 20 0 50 At t = 50 s, s /m displacement = ½(50)(20) = 500 m 2300 From t = 50 s to t = 130 s, 2100 displacement = 80 20 = 1600 m t / s From 500 t = 130 s to t = 150 s, t / s displacement = ½(20) = 200 m 0 50 130 150

Kinematics § 3. 1 Acceleration When an object’s velocity (not just speed) changes with time, it is said to undergo acceleration (or it is accelerating). Symbol: a Acceleration is a vector A change in velocity is brought about by: which points in the same Adirection change in only, i. e. speed changes asmagnitude v while direction remains constant. Acceleration has the S. I. unite. g. of moving metres per A change in direction only, in asecond circle 2). squared(m s with constant speed. A change in magnitude and direction simultaneously.

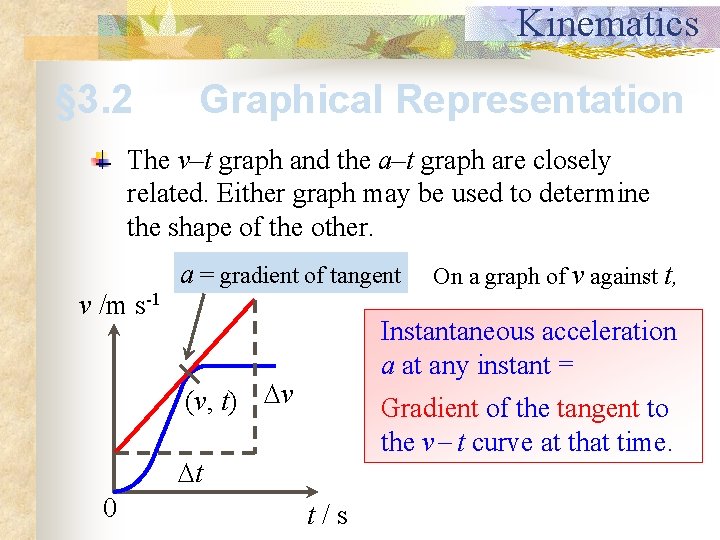
Kinematics § 3. 2 Graphical Representation The v–t graph and the a–t graph are closely related. Either graph may be used to determine the shape of the other. a = gradient of tangent v /m s-1 Instantaneous acceleration a at any instant = (v, t) v Gradient of the tangent to the v t curve at that time. t 0 On a graph of v against t, t/s

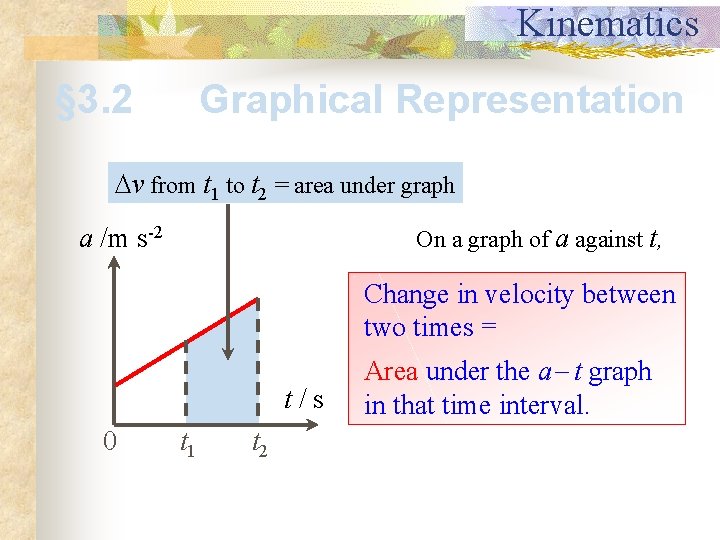
Kinematics § 3. 2 Graphical Representation v from t 1 to t 2 = area under graph a /m s-2 On a graph of a against t, Change in velocity between two times = t/s 0 t 1 t 2 Area under the a t graph in that time interval.

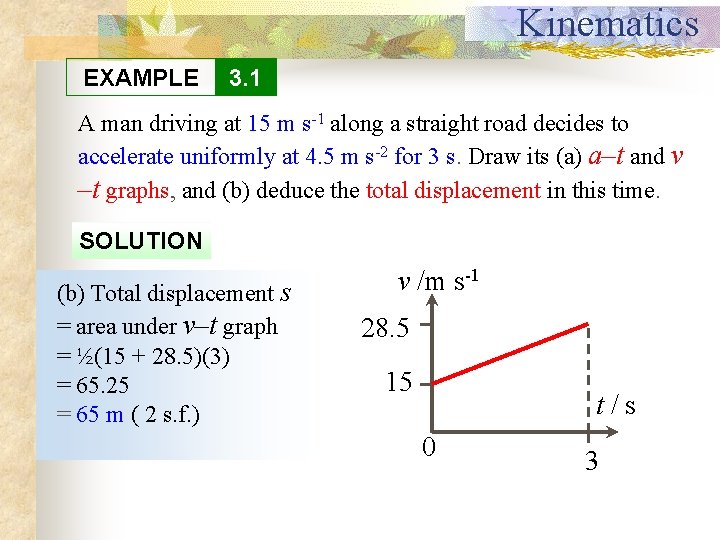
Kinematics EXAMPLE 3. 1 A man driving at 15 m s-1 along a straight road decides to accelerate uniformly at 4. 5 m s-2 for 3 s. Draw its (a) a–t and v –t graphs, and (b) deduce the total displacement in this time. SOLUTION Let initial velocity be u and final velocity be v, (b)a Total /m s-2 displacement s v /m sin velocity, v – u Change = area under a–t graph = at 28. 5 -1 = area under v–t graph =4. 5 ½(15 + 28. 5)(3) v = u + at = 15 + (4. 5)(3) t / s 15= 28. 5 m s 1 = 65. 25 t/s = 650 m ( 2 s. f. ) 3 A uniform acceleration velocity increases 0 3 at a constant rate, so the v–t graph is a straight line with a constant gradient.

Kinematics § 4 Uniform motion in a straight line Many situations occur in which the object’s acceleration is constant. One common e. g. is the motion of a freely falling object with negligible air resistance. Such motion is known as uniformly accelerated motion, where <a> = instantaneous acceleration.

Kinematics § 4. 1 Derivation of the Equations of Motion Consider an object moving in a straight line. At time t = 0, it has a velocity u. After moving for time t, its velocity increases to v. During this time its acceleration is a and its displacement is s. Using the definition of acceleration, a= v = u + at

Kinematics § 4. 1 The Equations of Motion As velocity varies linearly with time, we can express average velocity <v> as the arithmetic mean of u and v: v = u + at <v> = s Since <v> = t , s = <v>t 1 s = 2 (u + v)t

Kinematics § 4. 1 The Equations of Motion Substitute eqn 1 into eqn 2 to obtain another useful expression: v = u + at 1 s = (u + at)t 2 1 2 s = ut +2 at 1 s = 2 (u + v)t

Kinematics § 4. 1 The Equations of Motion Thet from 4 equations Eliminate eqns 1 apply and 2: strictly to motion with constant acceleration in a From eqn 1: t= straight line! ! v = u + at Subst. into eqn 2: that as time Recognise ! a remains sincreases, = 1 (uonly + v) 2 while s and v constant 2 aschanges. = v 2 – u 2 v 2 u 2 = + 2 as 1 s = 2 (u + v)t 1 2 s = ut +2 at

Kinematics § 4. 2 Using the Eqns of Motion Problem–solving technique: I D E A S Identify all given quantities, e. g. u, v, s, t draw a Diagram & define the origin and positive direction. choose the Equation that uses the given quantities. solve for the required Answer. consider Significance of answer, e. g. scalar/vector, +/ direction.

Kinematics EXAMPLE 4. 1 A speeding motorist driving at 15 m s-1 passes a school-crossing corner where the speed limit is 10 m s-1. He passes a stationary police officer on a motorcycle who immediately gives chase with an acceleration of 3. 0 m s-2. (a) How much time does the police officer take to catch up with the motorist? (b) What is the officer’s speed at that point? (c) Find the total distance travelled by each vehicle at that point.

Kinematics EXAMPLE 4. 1 SOLUTION Given: for the motorist, u 1 = 15 m s-1, a = 0 For the officer, u 2 = 0, a = 3. 0 m s-2 (a) For the motorist: For the officer: When (1) = (2): (b) For the officer, s = u 1 t = 15 t ……… (1) 1 3 s = u 2 t + 2 at 2 2 = 15 t = 3 t 2 t = 10 s t 2 ……… 2 v = u 2 + at = 0 + (3. 0)(10) = 30 m s-1 (c) Distance travelled by motorist (& officer), s = u 1 t = (15)(10) = 150 m

Kinematics § 4. 3 Free Fall The eqns derived the in § 4. 1 applied to objects Bodies fall towards Earthmay withbe constant acceleration. moving under the effect gravity. There are two main Such motion is referred to asoffree-fall. types of situations: The acceleration due to free-fall is denoted by the symbol g. -2, or 10 m s-2. g = 9. 81 m s-2 is, or 9. 8 m sand Object released allowed to fall under gravity. g is a vector always points downwards, Object that is projected vertically upwards regardless such that itof motionreaches of the object. a maximum height and then falls downwards again. We must assume the following: Air resistance is negligible or not present at all. Acceleration does not vary with altitude.

Kinematics EXAMPLE 4. 2 A stone is projected vertically upwards with a velocity of 20 m s-1 near the edge of the roof of a 50 m tall building. The stone just misses the edge and falls towards the ground. Taking g = 10 m s-2, determine (a) the time taken for the stone to reach its maximum height, (b) the maximum height reached, (c) the velocity and position of the stone 5. 0 s after projection, (d) the total time the stone is in the air.

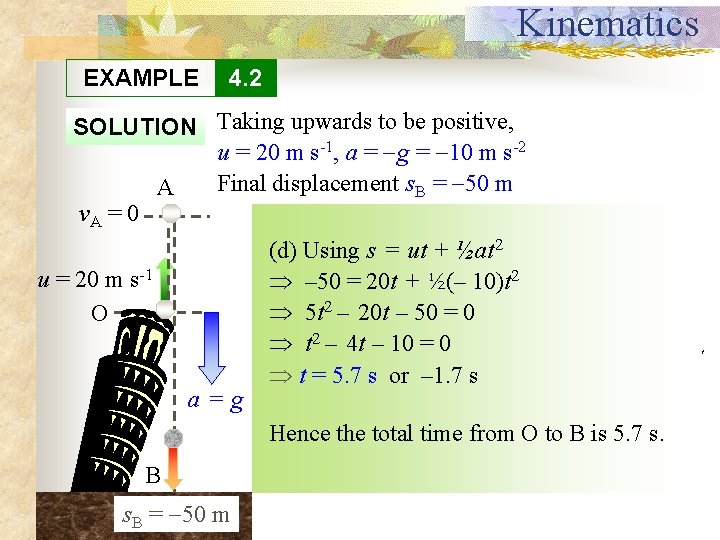
Kinematics EXAMPLE 4. 2 SOLUTION Taking upwards to be positive, u = 20 m s-1, a = g = 10 m s-2 Final displacement s. B = 50 m A v. A = 0 (a) its maximum = 0– 10(5. 0) (c)At Using v = u + atheight, 2 v v=A 20 (d) Using s = ut + ½at v = – 02 30 m –s-110 t Using v = u + at = 20 -1 u = 20 m s – 50 = 20 t + ½(– 10)t 2 t=2 s 2 Using s = ut + ½at 5 t – 20 t – 50 = 0 O 2 t 2 s– =4 t 20(5. 0) + ½(– 10)(5. 0) – 10 = 0 (b) Using v 2 = u 2 + 2 as 0 = 202 + 2(– 10)s = –s 25 t =s 5. 7 orm– 1. 7 ss= 20 m a = g Therefore, at t = 5. 0 s, the stone is 25 m below and is falling Hencethe theroof totaltop time from O to Bdownwards is 5. 7 s. at 30 m s-1. B s. B = 50 m

Kinematics § 4. 4 Effect of Air Resistance In reality, air resistance provides a retarding force which is not always negligible. The retarding force (or viscous force) acts opposite to the velocity. It is approximately proportional to v 2. We shall study the effect of air resistance on the motion of a body in air without going into detailed calculations.

Kinematics EXAMPLE 4. 3 With reference to example 4. 2, explain, without any calculations, how air resistance would affect (a) the time taken for the stone to reach its maximum height, (b) the maximum height reached, Discuss also how the motion of the stone would be different as it starts falling downwards towards the ground.

Kinematics SOLUTION (a) As the stone starts moving upwards, it experiences an effective downward acceleration which will be greater than g. u u Thus, v = u + at 0 = u (g + ar)t t = g + a < g r v=0 Therefore the time taken to reach the maximum height will be shorter. (b) Similarly, v 2 = u 2 + 2 as a = g + ar 2 2 u u 0 = u 2 2(g + ar)s s = < 2(g + ar) 2 g ar = additional u acceleration due to air resistance Therefore the greater downward acceleration will cause the stone to reach a lower maximum height.

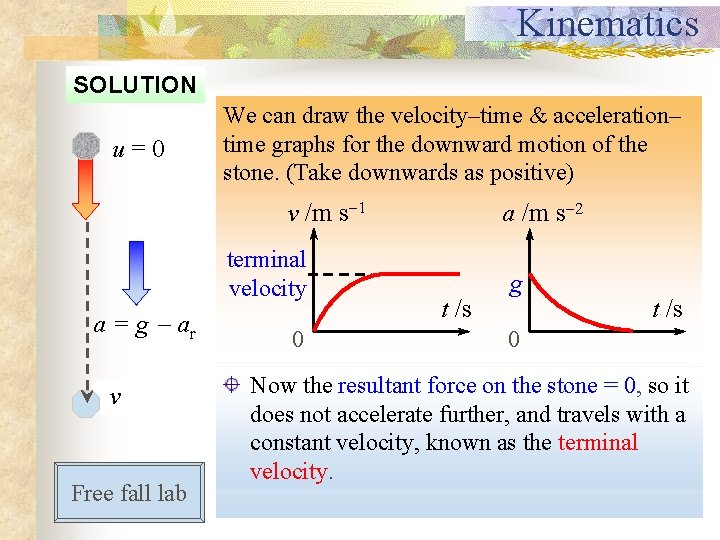
Kinematics SOLUTION u=0 a = g ar v Free fall lab At. After maximum height & acceleration– We can draw When the velocity–time some falling, time graphs for the downward motion of the stone. (Take downwards Retarding as positive) R = mg 1 force, a R/m<s 2 v /m s terminal velocity a = 0 a= a= g –g ar t /s weight mg 0 mg g t /s 0 For the downward motion, stone = starts Now As However, the stone resultant thefalls, stone’s force its speed on the increases, continues and to 0, sothe it falling from rest. retarding does increase, not accelerate causing force R Its due R further, toinitial to increase airdownward resistance andas travels well, with until a acceleration to mg). increases. constant upward force velocity, As=a. Rgresult, =(due downward known netweight as downward the force terminal mg. force and hence net acceleration (= g – ar) velocity. decreases.