New Insights into Covalent Enzyme Inhibition Application to

New Insights into Covalent Enzyme Inhibition Application to Anti-Cancer Drug Design Petr Kuzmič, Ph. D. Bio. Kin, Ltd. December 5, 2014 Brandeis University Covalent Inhibition Kinetics

Synopsis For a particular group of covalent (irreversible) protein kinase inhibitors: • Cellular potency is driven mainly by the initial noncovalent binding. • Chemical reactivity (covalent bond formation) plays only a minor role. • Of the two components of initial binding: - the association rate constant has a dominant effect, but - the dissociation rate constant appears unimportant. • These findings appear to contradict the widely accepted “residence time” hypothesis of drug potency. REFERENCE Schwartz, P. ; Kuzmic, P. et al. (2014) Proc. Natl. Acad. Sci. USA. 111, 173 -178. Covalent Inhibition Kinetics 2

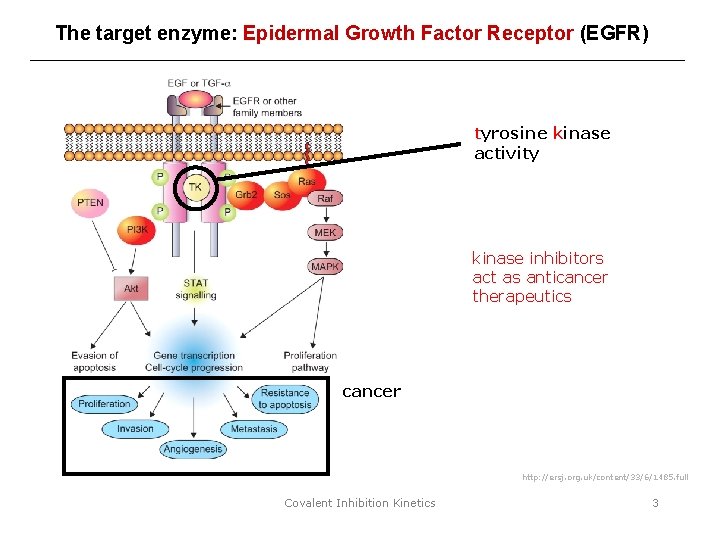
The target enzyme: Epidermal Growth Factor Receptor (EGFR) tyrosine kinase activity kinase inhibitors act as anticancer therapeutics cancer http: //ersj. org. uk/content/33/6/1485. full Covalent Inhibition Kinetics 3

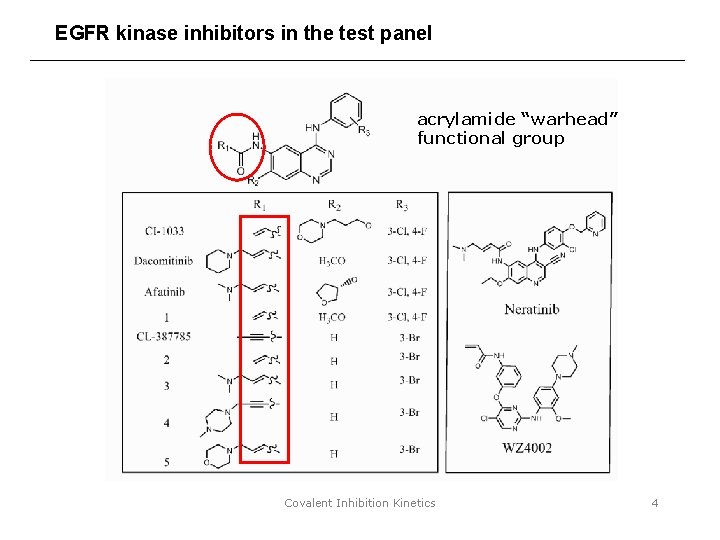
EGFR kinase inhibitors in the test panel acrylamide “warhead” functional group Covalent Inhibition Kinetics 4

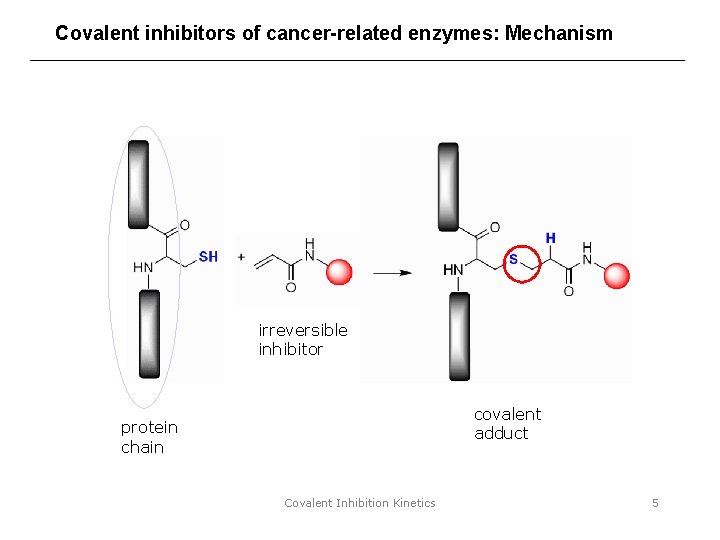
Covalent inhibitors of cancer-related enzymes: Mechanism irreversible inhibitor covalent adduct protein chain Covalent Inhibition Kinetics 5

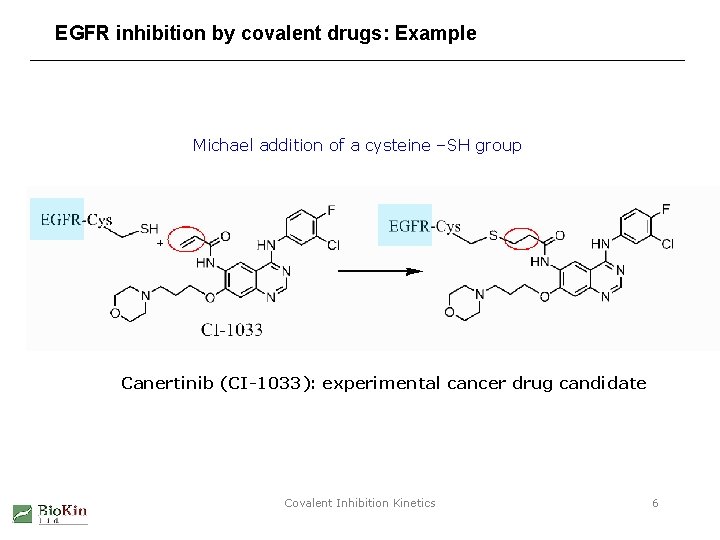
EGFR inhibition by covalent drugs: Example Michael addition of a cysteine –SH group Canertinib (CI-1033): experimental cancer drug candidate Covalent Inhibition Kinetics 6

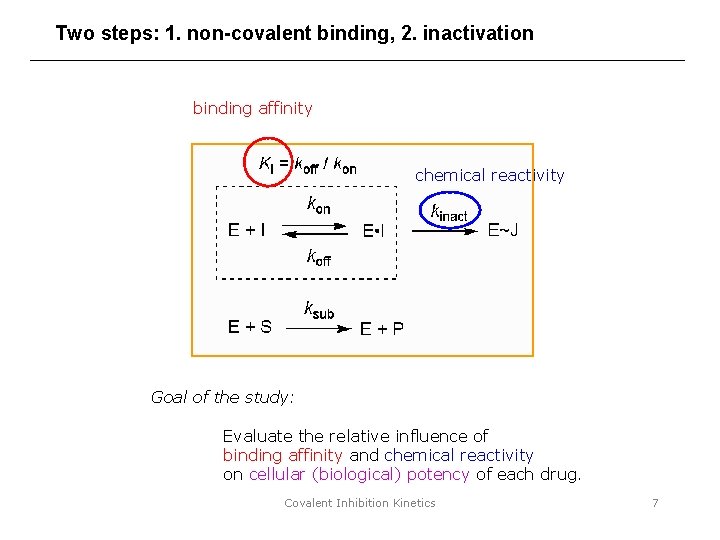
Two steps: 1. non-covalent binding, 2. inactivation binding affinity chemical reactivity Goal of the study: Evaluate the relative influence of binding affinity and chemical reactivity on cellular (biological) potency of each drug. Covalent Inhibition Kinetics 7

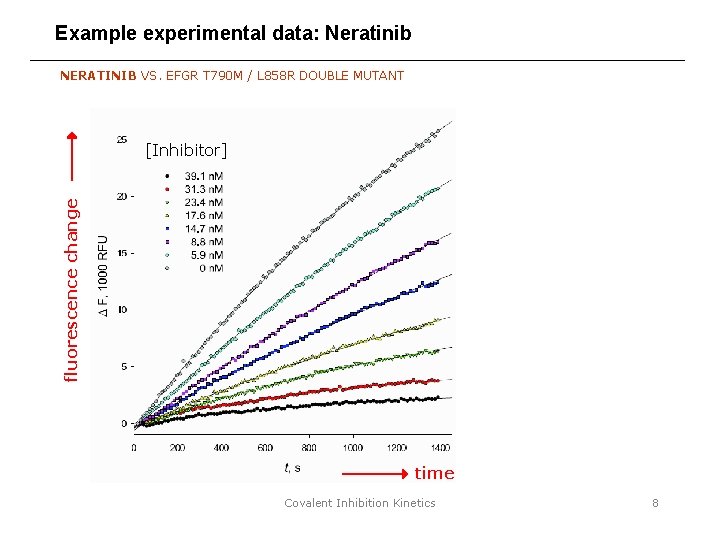
Example experimental data: Neratinib NERATINIB VS. EFGR T 790 M / L 858 R DOUBLE MUTANT fluorescence change [Inhibitor] time Covalent Inhibition Kinetics 8

Algebraic method of data analysis: Assumptions The “textbook” method (based on algebraic rate equations): Copeland R. A. (2013) “Evaluation of Enzyme Inhibitors in Drug Discovery”, 2 nd Ed. , Eq. (9. 1)(9. 2) ASSUMPTIONS: 1. Control progress curve ([I] = 0) must be strictly linear - Negligibly small substrate depletion over the entire time course 2. Negligibly small inhibitor depletion - Inhibitor concentrations must be very much larger than Ki Both of these assumptions are violated in our case. The “textbook” method of kinetic analysis cannot be used. Covalent Inhibition Kinetics 9

An alternate approach: Differential equation formalism “NUMERICAL” ENZYME KINETICS AND LIGAND BINDING Kuzmic, P. (2009) Meth. Enzymol. 467, 248 -280 Kuzmic, P. (1996) Anal. Biochem. 237, 260 -273 Covalent Inhibition Kinetics 10

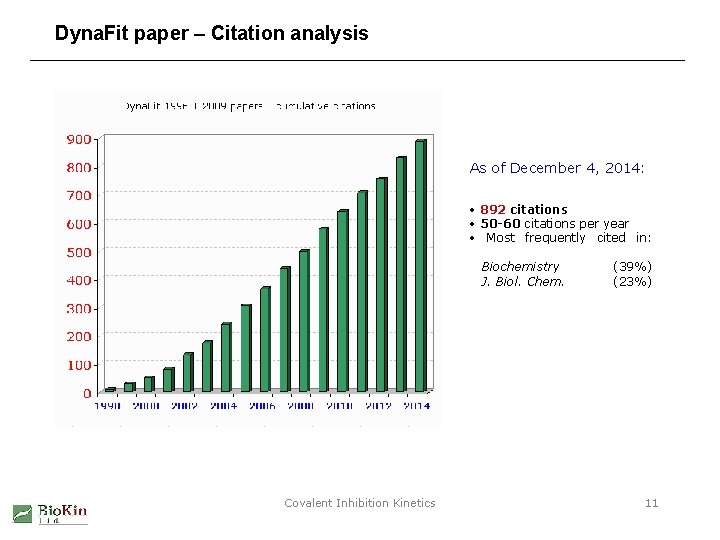
Dyna. Fit paper – Citation analysis As of December 4, 2014: • 892 citations • 50 -60 citations per year • Most frequently cited in: Biochemistry J. Biol. Chem. Covalent Inhibition Kinetics (39%) (23%) 11

A "Kinetic Compiler" HOW DYNAFIT PROCESSES YOUR BIOCHEMICAL EQUATIONS Rate terms: Input (plain text file): E + S ---> ES : k 1 [E] [S] ES ---> E + S : k 2 [ES] ES ---> E + P : k 3 [ES] Rate equations: d[E ] / dt = - k 1 [E] [S] + k 2 [ES] + k 3 [ES] d[ES ] / dt = + k 1 [E] [S] - k 2 [ES] - k 3 [ES] Similarly for other species. . . Covalent Inhibition Kinetics 12

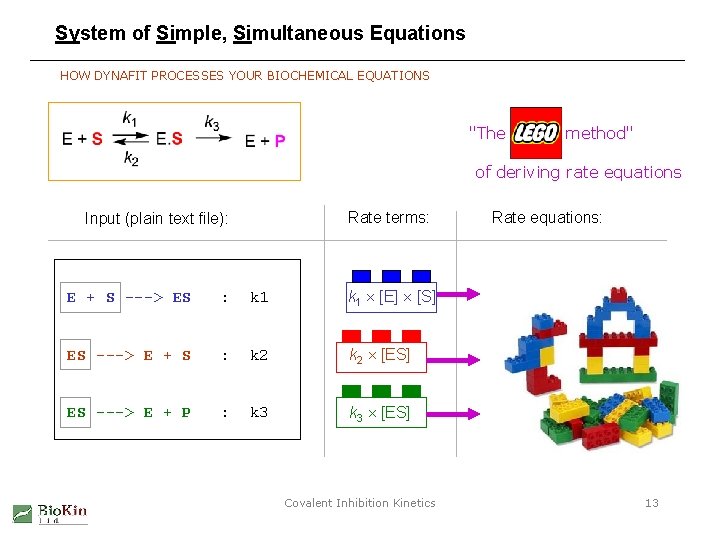
System of Simple, Simultaneous Equations HOW DYNAFIT PROCESSES YOUR BIOCHEMICAL EQUATIONS "The LEGO method" of deriving rate equations Rate terms: Input (plain text file): E + S ---> ES : k 1 [E] [S] ES ---> E + S : k 2 [ES] ES ---> E + P : k 3 [ES] Covalent Inhibition Kinetics Rate equations: 13

Dyna. Fit can analyze many types of experiments MASS ACTION LAW AND MASS CONSERVATION LAW IS APPLIED TO DERIVE DIFFERENT MODELS EXPERIMENT Reaction progress DYNAFIT DERIVES A SYSTEM OF. . . First-order ordinary differential equations Initial rates Nonlinear algebraic equations Equilibrium binding Nonlinear algebraic equations Covalent Inhibition Kinetics 14

The differential equation model of covalent inhibition This model is “integrated numerically”. Covalent Inhibition Kinetics 15

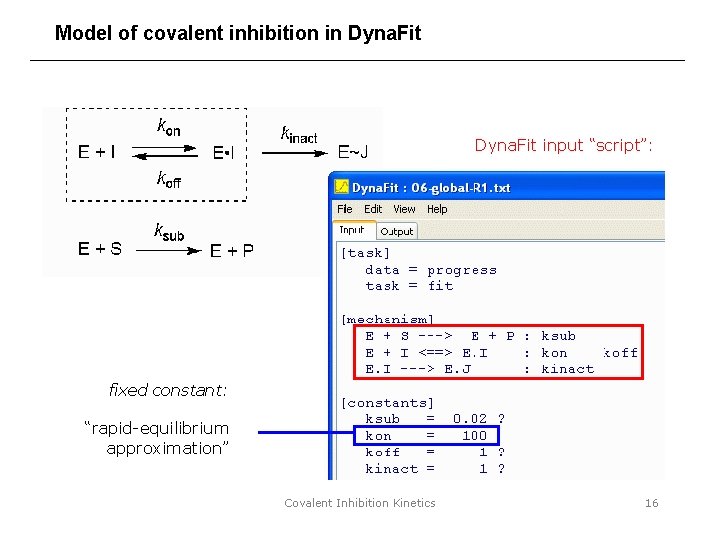
Model of covalent inhibition in Dyna. Fit input “script”: fixed constant: “rapid-equilibrium approximation” Covalent Inhibition Kinetics 16

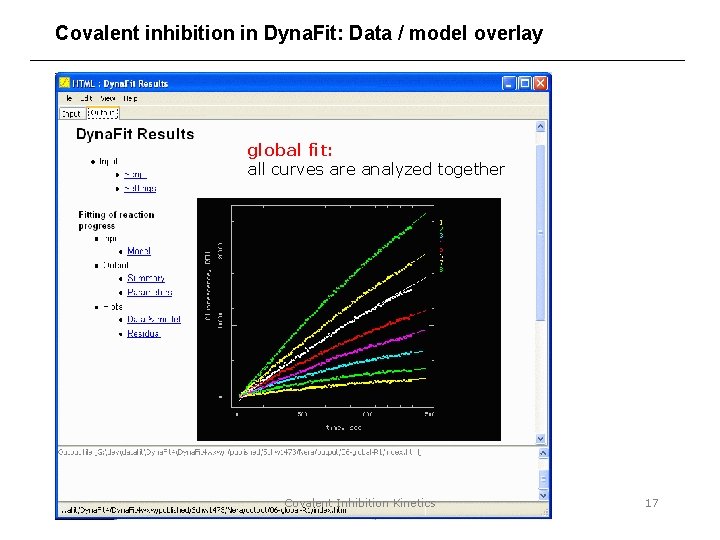
Covalent inhibition in Dyna. Fit: Data / model overlay global fit: all curves are analyzed together Covalent Inhibition Kinetics 17

Covalent inhibition in Dyna. Fit: Model parameters Dyna. Fit output window: How do we get Ki out of this? • Recall that kon was arbitrarily fixed at 100 µM-1 s-1 (“rapid equilibrium”) Ki = koff/kon = 0. 341 / 100 = 0. 00341 µM = 3. 4 n. M Covalent Inhibition Kinetics 18

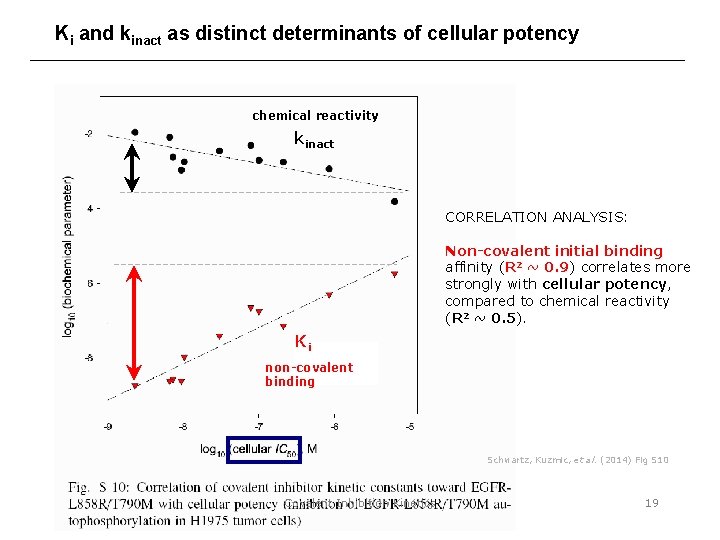
Ki and kinact as distinct determinants of cellular potency chemical reactivity kinact CORRELATION ANALYSIS: Non-covalent initial binding affinity (R 2 ~ 0. 9) correlates more strongly with cellular potency, compared to chemical reactivity (R 2 ~ 0. 5). Ki non-covalent binding Schwartz, Kuzmic, et al. (2014) Fig S 10 Covalent Inhibition Kinetics 19

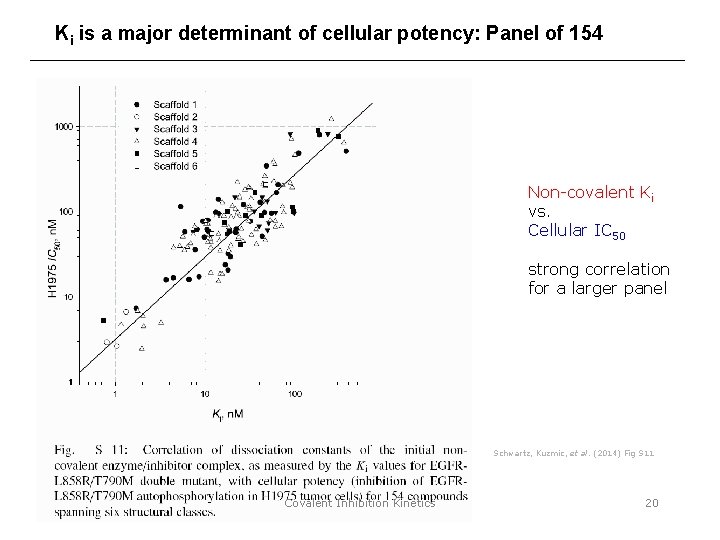
Ki is a major determinant of cellular potency: Panel of 154 Non-covalent Ki vs. Cellular IC 50 strong correlation for a larger panel Schwartz, Kuzmic, et al. (2014) Fig S 11 Covalent Inhibition Kinetics 20

Overall conclusions, up to this point Non-covalent initial binding appears more important than chemical reactivity for the cellular potency of this particular panel of 11 covalent anticancer drugs. Proc. Natl. Acad. Sci. USA. 111, 173 -178 (2014). Covalent Inhibition Kinetics 21

THE NEXT FRONTIER: MICROSCOPIC “ON” AND “OFF” RATE CONSTANTS Covalent Inhibition Kinetics 22

Confidence intervals for “on” / “off” rate constants • We cannot determine “on” and “off” constants from currently available data. • But we can estimate at least the lower limits of their confidence intervals. METHOD: “Likelihood profile” a. k. a. “Profile-t” method REFERENCES: 1. Watts, D. G. (1994) "Parameter estimates from nonlinear models“ Methods in Enzymology, vol. 240, pp. 23 -36 2. Bates, D. M. , and Watts, D. G. (1988) Nonlinear Regression Analysis and its Applications John Wiley, New York sec. 6. 1 (pp. 200 -216) - two biochemical examples Covalent Inhibition Kinetics 23

Likelihood profile method: Computational algorithm 1. Perform nonlinear least-squares fit with the full set of model parameters. 2. Progressively increase a parameter of interest, P, away from its best-fit value. From now on keep P fixed in the fitting model. 3. At each step optimize the remaining model parameters. 4. Continue stepping with P until the sum of squares reaches a critical level. 5. This critical increase marks the upper end of the confidence interval for P. 6. Go back to step #2 and progressively decrease P, to find the lower end of the confidence interval. Watts, D. G. (1994) "Parameter estimates from nonlinear models“ Methods in Enzymology, vol. 240, pp. 23 -36 Covalent Inhibition Kinetics 24

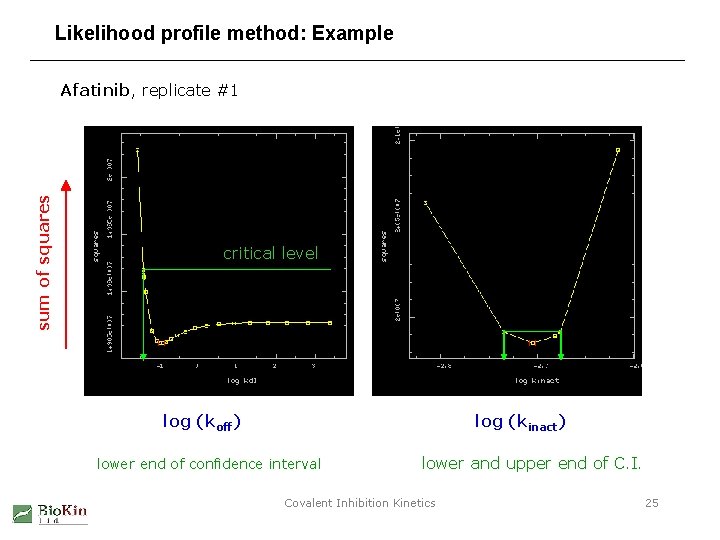
Likelihood profile method: Example sum of squares Afatinib, replicate #1 critical level log (koff) log (kinact) lower end of confidence interval lower and upper end of C. I. Covalent Inhibition Kinetics 25

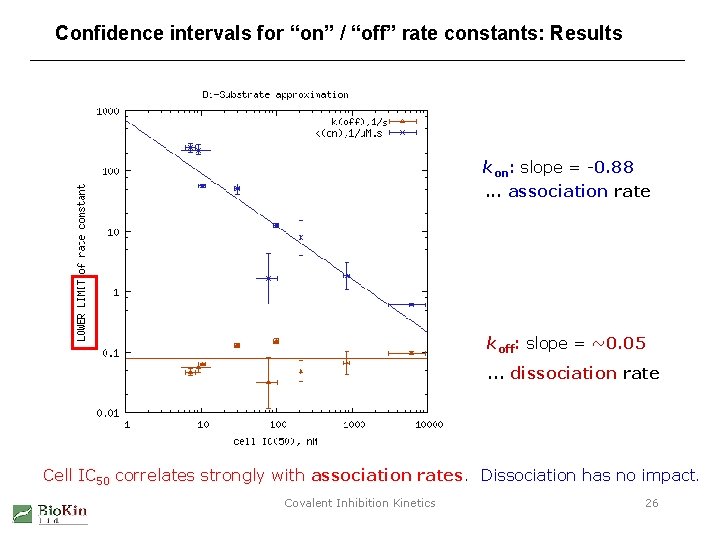
Confidence intervals for “on” / “off” rate constants: Results s kon: slope = -0. 88. . . association rate koff: slope = ~0. 05. . . dissociation rate Cell IC 50 correlates strongly with association rates. Dissociation has no impact. Covalent Inhibition Kinetics 26

Lower limits vs. “true” values of rate constants • We assumed that the lower limits for kon and koff are relevant proxies for “true” values. • One way to validate this is via Monte-Carlo simulations: 1. Simulate many articificial data sets where the “true” value is known. 2. Fit each synthetic data set and determine confidence intervals. 3. Compare “true” (i. e. simulated) values with lower limits. • Preliminary Monte-Carlo results confirm our assumptions. • Additional computations are currently ongoing. Covalent Inhibition Kinetics 27

Cellular potency vs. upper limit of “residence time” “Drug-receptor residence time”: t = 1 / koff • Lower limit for “off” rate constant defines the upper limit for residence time. • Both minimum koff and maximum t is invariant across our compound panel. • However cellular IC 50 varies by 3 -4 orders of magnitude. • This is unexpected in light of the “residence time” theory of drug potency. Covalent Inhibition Kinetics 28

“Residence time” hypothesis of drug efficacy SEMINAL PAPERS: • Copeland, Pompliano & Meek (2006) Nature Rev. Drug Disc. 5, 730 • Tummino & Copeland (2008) Biochemistry 47, 5481 • Copeland (2011) Future Med. Chem. 3, 1491 EXAMPLE SYSTEMS: • work from Peter Tonge’s lab (SUNY Stony Brook) ILLUMINATING DISCUSSION: • Dahl & Akerud (2013) Drug Disc. Today 18, 697 -707 Covalent Inhibition Kinetics 29

Summary and conclusions: Biochemical vs. cellular potency 1. EQUILIBRIUM BINDING AFFINITY: Initial (non-covalent) binding seems more important for cell potency than chemical reactivity. 2. BINDING DYNAMICS: Association rates seem more important for cell potency than dissociation rates (i. e. , “residence time”). CAVEAT: We only looked at 11 inhibitors of a single enzyme. Additional work is needed to confirm our findings. Covalent Inhibition Kinetics 30

Acknowledgments • Brion Murray Pfizer Oncology La Jolla, CA • Philip Schwartz* • Jim Solowiej * Currently Takeda Pharma San Diego, CA This presentation is available for download at www. biokin. com biochemical kinetics Covalent Inhibition Kinetics 31

SUPPLEMENTARY SLIDES Covalent Inhibition Kinetics 32

CHECK UNDERLYING ASSUMPTIONS: BIMOLECULAR ASSOCIATION RATE Covalent Inhibition Kinetics 33

Differential equation method: Example – Afatinib: Parameters DYNAFIT-GENERATED OUTPUT recall: we assumed this value Ki = kd. I / ka. I = 10 µM-1 s-1. . . assumed (fixed constant) Could the final result be skewed by making an arbitrary assumption about the magnitude of the association rate constant? Covalent Inhibition Kinetics 34

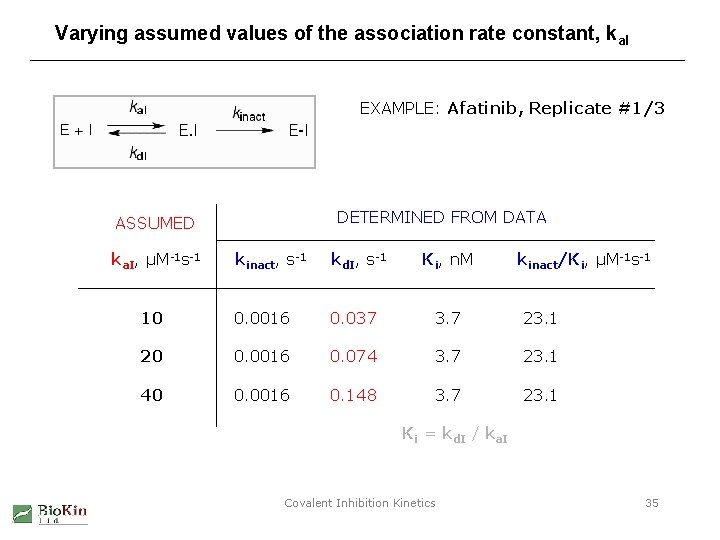
Varying assumed values of the association rate constant, ka. I EXAMPLE: Afatinib, Replicate #1/3 DETERMINED FROM DATA ASSUMED ka. I, µM-1 s-1 kinact, s-1 kd. I, s-1 Ki, n. M kinact/Ki, µM-1 s-1 10 0. 0016 0. 037 3. 7 23. 1 20 0. 0016 0. 074 3. 7 23. 1 40 0. 0016 0. 148 3. 7 23. 1 Ki = kd. I / ka. I Covalent Inhibition Kinetics 35

Effect of assumed association rate constant: Conclusions The assumed value of the “on” rate constant • does effect the best-fit value of the dissociation (“off”) rate constant, kd. I. • The fitted value of kd. I increases proportionally with the assumed value of ka. I. • Therefore the best-fit value of the inhibition constant, Ki, remains invariant. • The inactivation rate constant, kinact, remains unaffected. Assumptions about the “on” rate constant have no effect on the best-fit values of kinact, Ki, and kinact/Ki. However, the dissociation (“off”) rate constant remains undefined by this type of data. Covalent Inhibition Kinetics 36

CHECK UNDERLYING ASSUMPTIONS: SUBSTRATE MECHANISM Covalent Inhibition Kinetics 37

Substrate mechanism – “Hit and Run” ASSUMING THAT THE MICHAELIS COMPLEX CONCENTRATION IS EFFECTIVELY ZERO • Justified by assuming that [S]0 << KM • In our experiments KM ≥ 220 µM and [S]0 = 13 µM • The model was used in Schwartz et al. 2014 (PNAS) Covalent Inhibition Kinetics 38

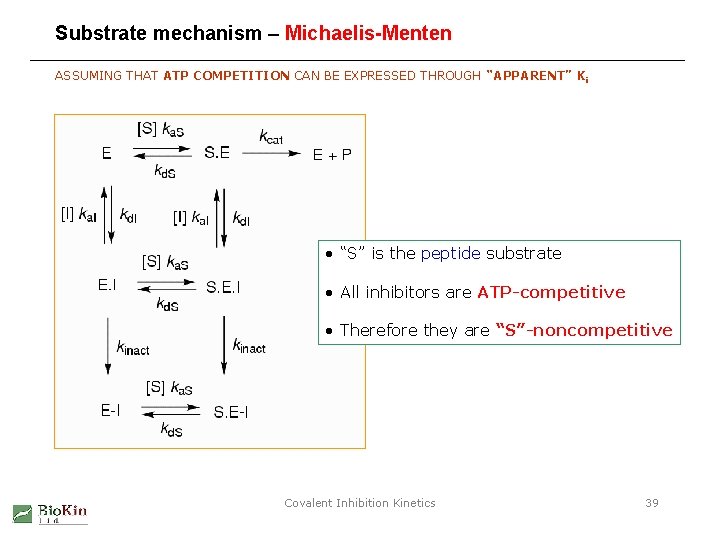
Substrate mechanism – Michaelis-Menten ASSUMING THAT ATP COMPETITION CAN BE EXPRESSED THROUGH “APPARENT” Ki • “S” is the peptide substrate • All inhibitors are ATP-competitive • Therefore they are “S”-noncompetitive Covalent Inhibition Kinetics 39

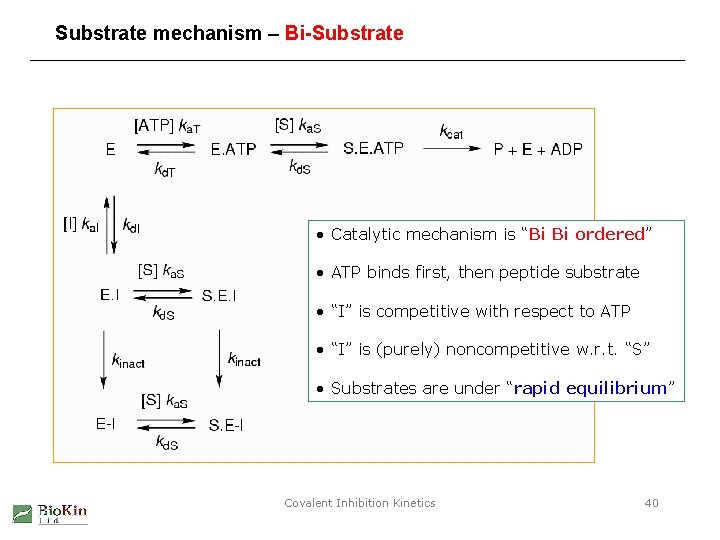
Substrate mechanism – Bi-Substrate • Catalytic mechanism is “Bi Bi ordered” • ATP binds first, then peptide substrate • “I” is competitive with respect to ATP • “I” is (purely) noncompetitive w. r. t. “S” • Substrates are under “rapid equilibrium” Covalent Inhibition Kinetics 40

Substrate mechanism – “Bi-Substrate”: Dyna. Fit notation MECHANISM: DYNAFIT INPUT: [mechanism] E + ATP <==> E. ATP : ka. T kd. T S + E. ATP <==> S. E. ATP : ka. S kd. S S. E. ATP ---> P + E + ADP : kcat E + I <==> E. I : ka. I E. I ---> E-I : kinact kd. I Similarly for the remaining steps in the mechanism. Covalent Inhibition Kinetics 41

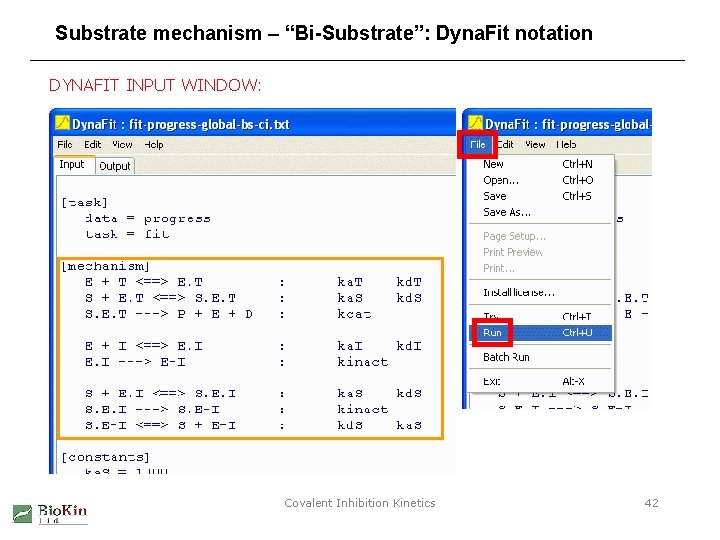
Substrate mechanism – “Bi-Substrate”: Dyna. Fit notation DYNAFIT INPUT WINDOW: Covalent Inhibition Kinetics 42

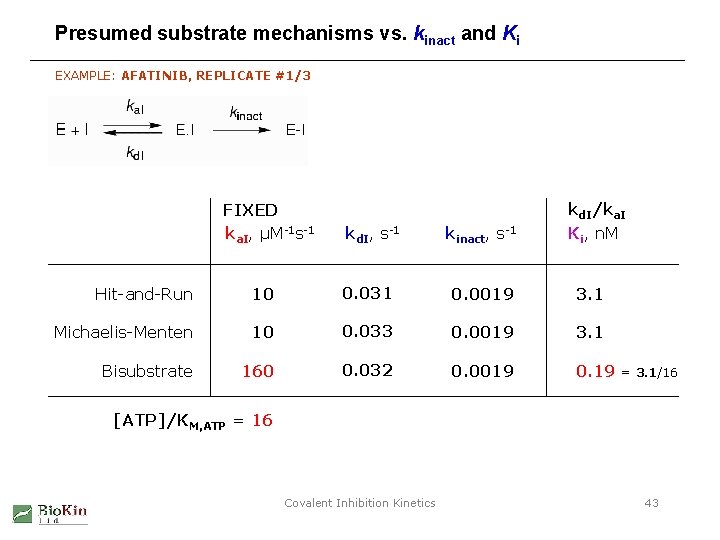
Presumed substrate mechanisms vs. kinact and Ki EXAMPLE: AFATINIB, REPLICATE #1/3 FIXED ka. I, µM-1 s-1 kd. I, s-1 kinact, s-1 kd. I/ka. I Ki, n. M Hit-and-Run 10 0. 031 0. 0019 3. 1 Michaelis-Menten 10 0. 033 0. 0019 3. 1 Bisubstrate 160 0. 032 0. 0019 0. 19 = 3. 1/16 [ATP]/KM, ATP = 16 Covalent Inhibition Kinetics 43

Substrate mechanism – Summary 1. Basic characteristic of inhibitors (Ki, kinact) are essentially independent on the presumed substrate mechanism. 2. The inactivation rate constant (kinact) is entirely invariant across all three substrate mechanisms. 3. The initial binding affinity (Ki) needs to be corrected for ATP competition in the case of “Hit and Run” and “Michaelis-Menten” mechanisms: - Hit-and-Run or Michaelis-Menten: Divide the measured Kiapp value by [ATP]/KM, ATP to obtain true Ki - Bisubstrate: True Ki is obtained directly. Covalent Inhibition Kinetics 44

THEORETICAL ASSUMPTIONS VIOLATED: CLASSIC ALGEBRAIC METHOD Covalent Inhibition Kinetics 45

Check concentrations: “Tight binding” or not? [Inhibitor] [Enzyme] 20 n. M The assumption that [Inhibitor] >> [Enzyme] clearly does not hold. We have “tight binding”, making it impossible to utilize the classic algebraic method. Covalent Inhibition Kinetics 46

Check linearity of control progress curve ([Inhibitor] = 0) This “slight” nonlinearity has a massive impact, making it impossible to utilize the classic algebraic method: REFERENCE: Kuzmic et al. (2015) “An algebraic model for the kinetics of covalent enzyme inhibition at low substrate concentrations” Anal. Biochem. , in press Manuscript No. ABIO-14 -632 Covalent Inhibition Kinetics 47

ACRYLAMIDE WARHEAD: STRUCTURE VARIATION VS. kinact Covalent Inhibition Kinetics 48

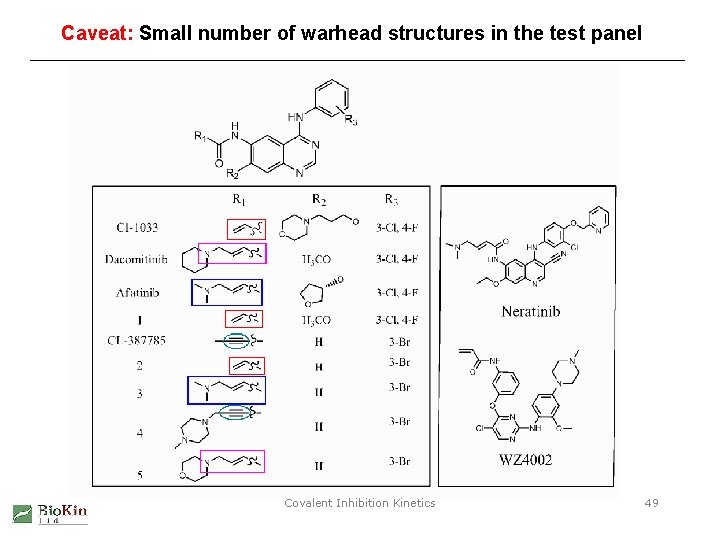
Caveat: Small number of warhead structures in the test panel Covalent Inhibition Kinetics 49

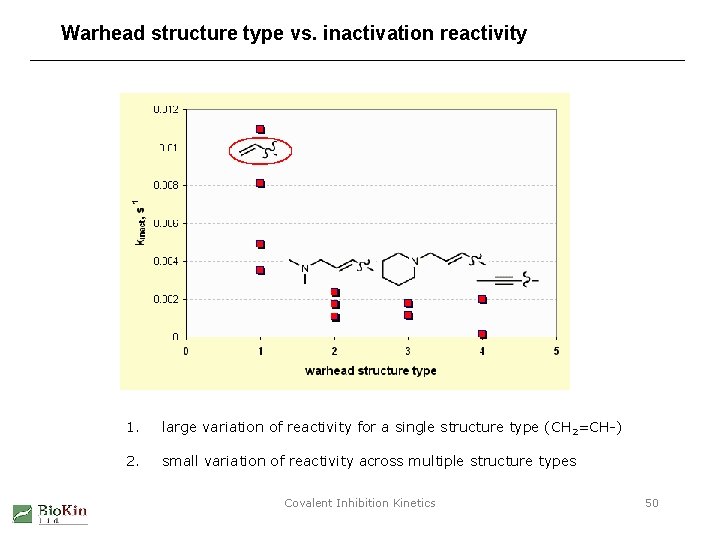
Warhead structure type vs. inactivation reactivity 1. large variation of reactivity for a single structure type (CH 2=CH-) 2. small variation of reactivity across multiple structure types Covalent Inhibition Kinetics 50