New framework for supply chain decision making under

New framework for supply chain decision making under uncertainty: An analysis of the computational effort (All IP patent pending under PCT) Abhilasha Aswal G. N. Srinivasa Prasanna Infosys Technologies Limited, Bangalore, India Email: abhilasha_aswal@infosys. com International Institute of Information Technology, Bangalore, India Email: gnsprasanna@iiitb. ac. in 23 rd European Conference on Operational Research, Bonn, 2009

Outline q Introduction q Models for handling uncertainty q Our model: Extension of robust optimization Ø Capabilities (simple to input specifications, quantify it, and see its relations to other possible specifications) q Problem formulation q Computational Results q Conclusions 23 rd European Conference on Operational Research, Bonn, 2009

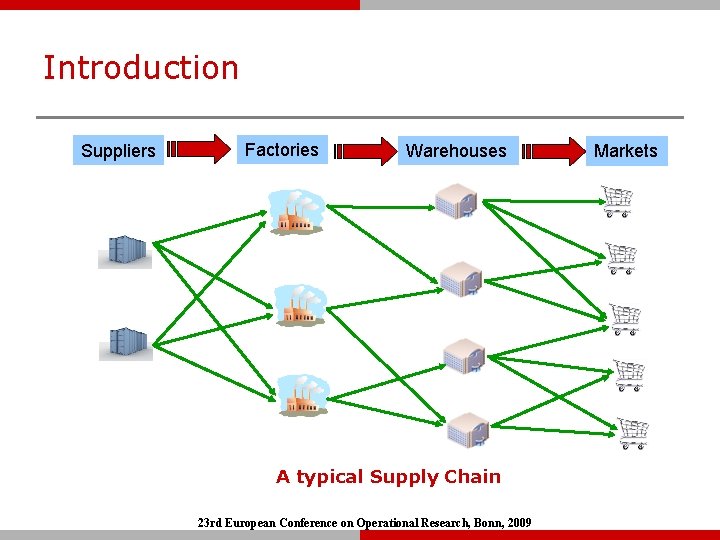
Introduction Suppliers Factories Warehouses A typical Supply Chain 23 rd European Conference on Operational Research, Bonn, 2009 Markets

Introduction q Major Issue in Supply Chains: Uncertainty Ø A supply chain necessarily involves decisions about future operations. § Coordination of production, inventory, location, transportation to achieve the best mix of responsiveness and efficiency. Ø Decisions made using typically uncertain information. § Uncertain Demand, supplier capacity, prices. . etc § Forecasting demand for a large number of commodities is difficult, especially for new products. 23 rd European Conference on Operational Research, Bonn, 2009

Models for handling uncertainty in supply chains q Deterministic Model Ø A-priori knowledge of parameters Ø Does not address uncertainty q Stochastic / Dynamic Programming Ø Uncertain data represented as random variables with a known distribution. Ø Information required to estimate: Ø All possible outcomes: usually exponential or infinite Ø Probability of an outcome Ø How to estimate? q Robust Optimization Ø Uncertain data represented as uncertainty sets. Ø Less information required. Ø How to choose the right uncertainty set? 23 rd European Conference on Operational Research, Bonn, 2009

Our model: Extension of robust optimization 23 rd European Conference on Operational Research, Bonn, 2009

Convex polyhedral formulation q Uncertain parameters bounded by polyhedral uncertainty sets (extendible to convex polyhedral sets). Ø Linear constraints that model microeconomic behavior Ø Parameter estimates based on ad-hoc assumptions avoided, constraints used as is. Ø Aggregates, Substitutive and Complementary behavior. q A hierarchy of scenarios sets Ø A set of linear constraints specify a scenario set. Ø Scenario sets can each have an infinity of scenarios § Intuitive Scenario Hierarchy § Based on Aggregate Bounds § Underlying Economic Behavior 23 rd European Conference on Operational Research, Bonn, 2009

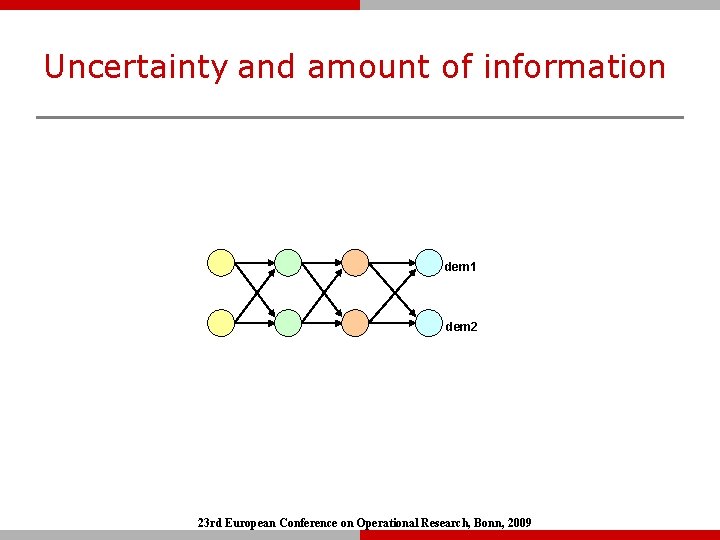
Representation of uncertainty q Information easily provided by Economically Meaningful Constraints Ø Economic behavior is easily captured in terms of types of goods, complements and substitutes. § Substitutive goods 10 <= d 1 + d 2 + d 3 <= 20 – d 1, d 2 and d 3 are demands for 3 substitutive goods. § Complementary/competitive goods -10 <= d 1 - d 2 <= 10 – d 1 and d 2 are demands for 2 complementary goods. § Profit/Revenue Constraints 20 <= 6. 1 d 1 + 3. 8 d 3 <= 40 – Price of a product times its demand revenue. This constraint puts limits on the total revenue. 23 rd European Conference on Operational Research, Bonn, 2009

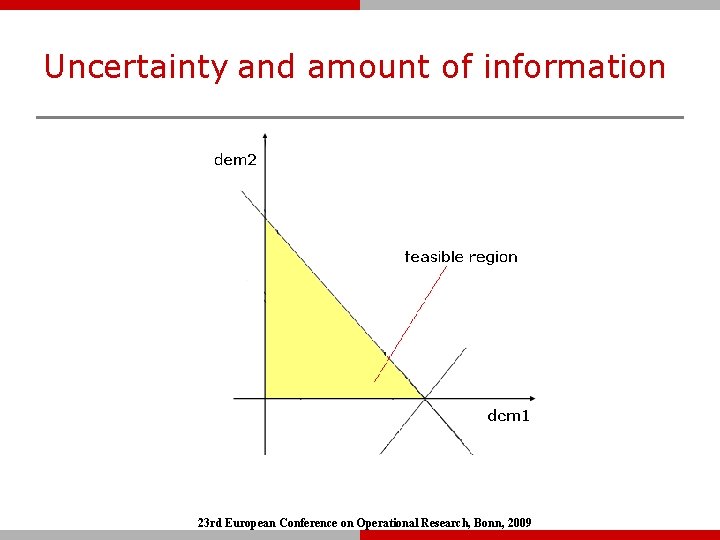
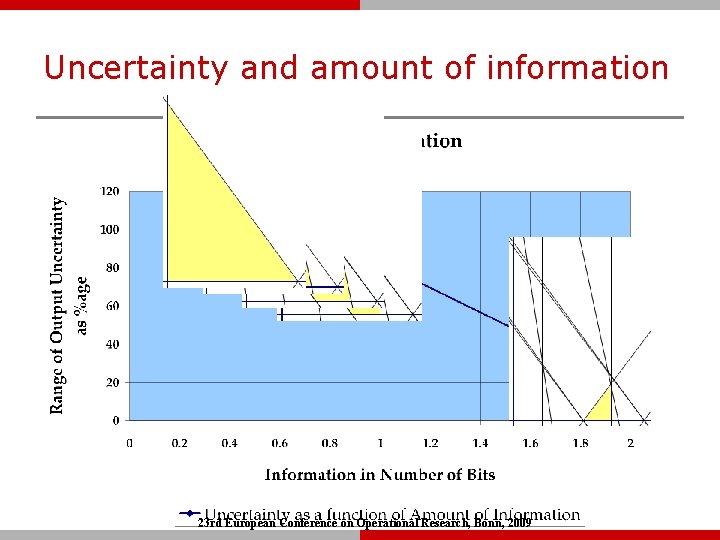
Quantification of Information content q Information is provided in the form of constraint sets. q These constraint sets form a polytope, of Volume V 1 q The volume measures the total number of scenarios being considered. q No of bits = log 2 (VREF/V 1) q Quantitative comparison of different Scenario sets Ø Quantitative Estimate of Uncertainty. Ø Generation of equivalent information. Ø Both input and output information. Img source: http: //en. wikipedia. org/wiki/File: Dodecahedron. gif 23 rd European Conference on Operational Research, Bonn, 2009

Uncertainty and amount of information dem 1 dem 2 23 rd European Conference on Operational Research, Bonn, 2009

Uncertainty and amount of information 23 rd European Conference on Operational Research, Bonn, 2009

Uncertainty and amount of information 23 rd European Conference on Operational Research, Bonn, 2009

Relational algebra of polytopes q Relationships between different scenario sets using the relational algebra of polytopes Ø One set is a sub-set of the other Ø Two constraint sets intersect Ø The two constraint sets are. Intersection disjoint Subset Disjointedness q A general query based on the set-theoretic relations above can also be given, e. g. Ø “A Subset (B Intersection C)? ”: checks if the intersection of B and C encloses A. 23 rd European Conference on Operational Research, Bonn, 2009

Related work q Bertsimas, Sim, Thiele - “Budget of uncertainty” (amongst Nemirovksi/Ben Tal/Shapiro/El Ghaoui/Lebret) Ø Uncertainty: Ø Normalized deviation for a parameter: Ø Sum of all normalized deviations limited: Ø N uncertain parameters polytope with 2 N sides Ø In contrast, our polyhedral uncertainty sets: § More general § Much fewer sides 23 rd European Conference on Operational Research, Bonn, 2009

Problem formulation Static capacity planning (simplified) 23 rd European Conference on Operational Research, Bonn, 2009

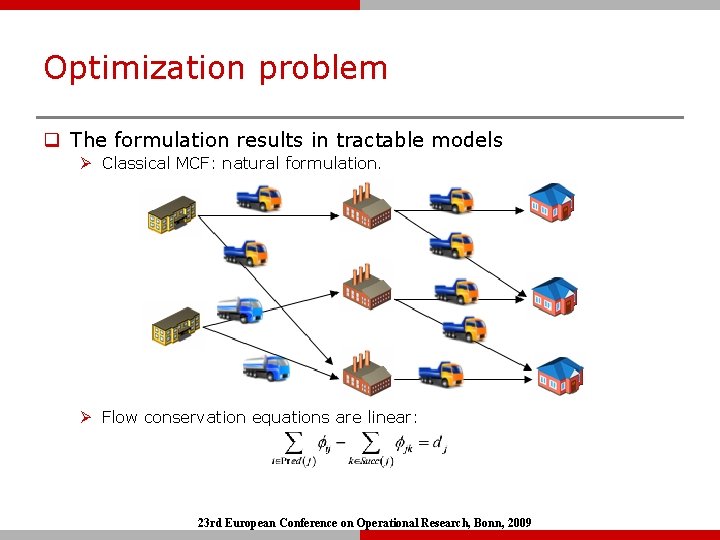
Optimization problem q The formulation results in tractable models Ø Classical MCF: natural formulation. Ø Flow conservation equations are linear: 23 rd European Conference on Operational Research, Bonn, 2009

Optimization problem q Matrix form of flow equations: AΦ ≤ d Ø Ø Ø A: unimodular flow conservation matrix d: source/sink values Φ: flow vector [ΦS, ΦD, ΦI] ΦS: flow vector from the suppliers ΦD: (variable) demand ΦI: inventory q Hence, a generic supply chain optimization: Min CTΦ AΦ ≤ d Φ≥ 0 23 rd European Conference on Operational Research, Bonn, 2009

Optimization problem q Uncertainty in the right hand side Ø When uncertainty is introduced, right hand side B becomes a variable (and moves to the l. h. s), yielding the formal LP: Min CTΦ (CP)T d ≤ E Φ≥ 0 Ø The (CP)T d ≤ E represents the linear uncertainty constraints of our specification. 23 rd European Conference on Operational Research, Bonn, 2009

Finding absolute bounds q Absolute bounds on performance quickly found Ø Best performance in best case of the uncertain parameters LP Ø Worst performance in worst case of the uncertain parameters LP 23 rd European Conference on Operational Research, Bonn, 2009

Finding optimal solutions q Optimal flow Φ Ø Minimizes the cost in the worst case of the uncertain parameters. q min-max optimization not an LP. 23 rd European Conference on Operational Research, Bonn, 2009

Finding optimal solutions q Duality? ? Ø No breakpoints or fixed costs: min-max optimization QP QP 23 rd European Conference on Operational Research, Bonn, 2009

Finding optimal solutions q Duality? ? Ø Linear costs and variable locations QP QP } 23 rd European Conference on Operational Research, Bonn, 2009

Finding optimal solutions q Duality? ? Ø Fixed costs and breakpoints: non-convexities that preclude strong-duality from being achieved. Cost B 1 B 2 Quantity q Finding absolute bounds is relatively easy using state-of-art solvers q Min-max bound tightening heuristics have to be used in general 23 rd European Conference on Operational Research, Bonn, 2009

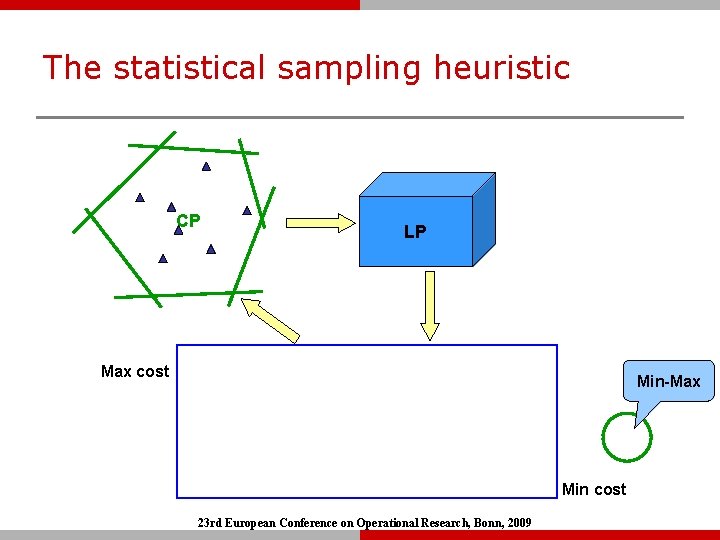
The statistical sampling heuristic q First, the performance is bounded by finding absolute bounds (min-min and max-max solutions) Ø These can be found directly by min/max ILP) q A number of demand samples are chosen at random and optimal policies for each is computed. Ø The problem of finding the optimal policy for a deterministic demand sample is an LP/ILP. q The one having the lowest worst case cost is selected. 23 rd European Conference on Operational Research, Bonn, 2009

The statistical sampling heuristic CP LP Max cost Min-Max Min cost 23 rd European Conference on Operational Research, Bonn, 2009

Experimental Results q All problems solved using Ø A typical laptop: § Intel Celeron 1. 60 GHz processor, with a 512 MB RAM Ø ILOG CPLEX 11. 0 solver 23 rd European Conference on Operational Research, Bonn, 2009

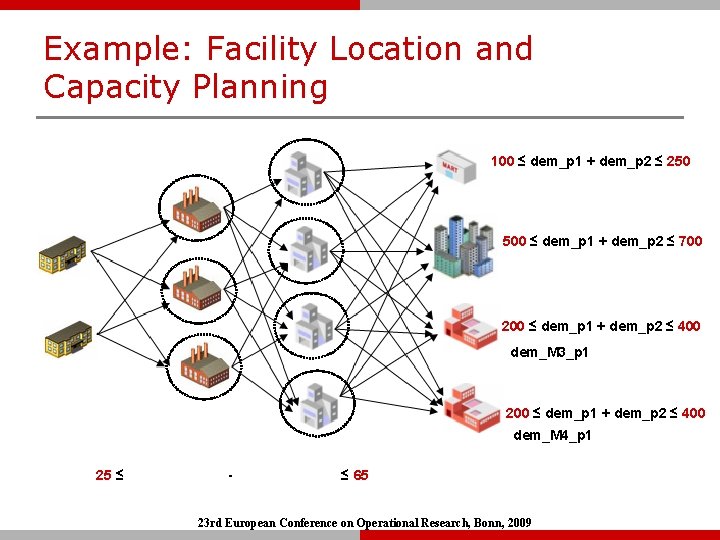
Example: Facility Location and Capacity Planning 100 ≤ dem_p 1 + dem_p 2 ≤ 250 500 ≤ dem_p 1 + dem_p 2 ≤ 700 200 ≤ dem_p 1 + dem_p 2 ≤ 400 dem_M 3_p 1 200 ≤ dem_p 1 + dem_p 2 ≤ 400 dem_M 4_p 1 25 ≤ - ≤ 65 23 rd European Conference on Operational Research, Bonn, 2009

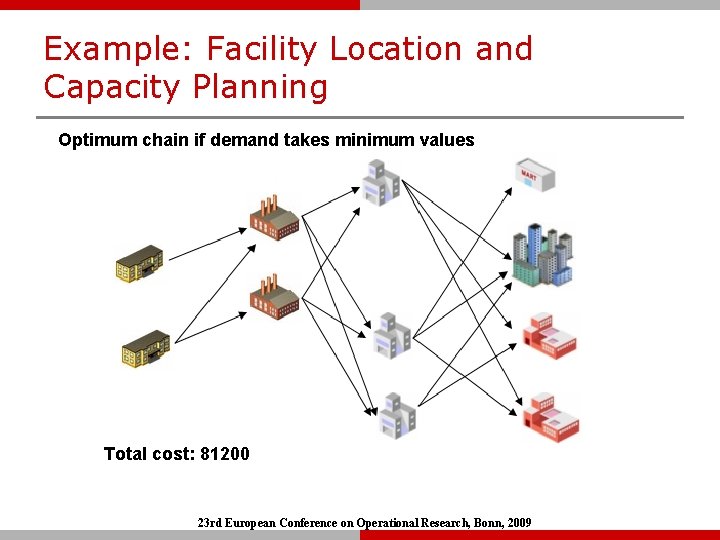
Example: Facility Location and Capacity Planning Optimum chain if demand takes minimum values Total cost: 81200 23 rd European Conference on Operational Research, Bonn, 2009

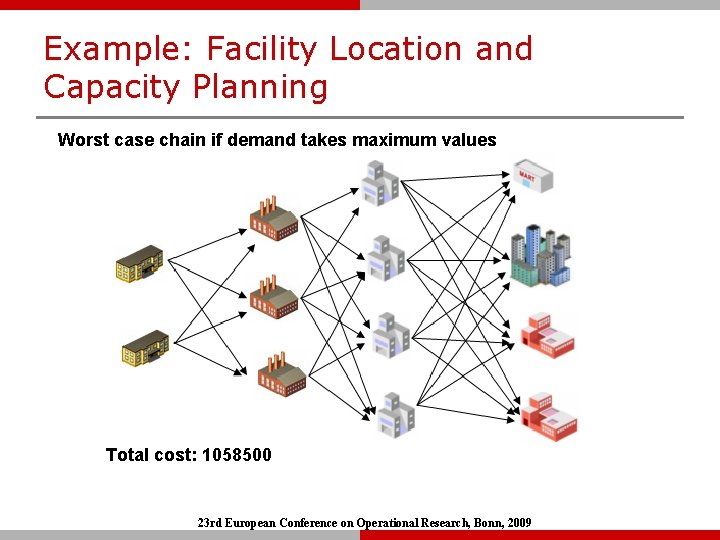
Example: Facility Location and Capacity Planning Worst case chain if demand takes maximum values Total cost: 1058500 23 rd European Conference on Operational Research, Bonn, 2009

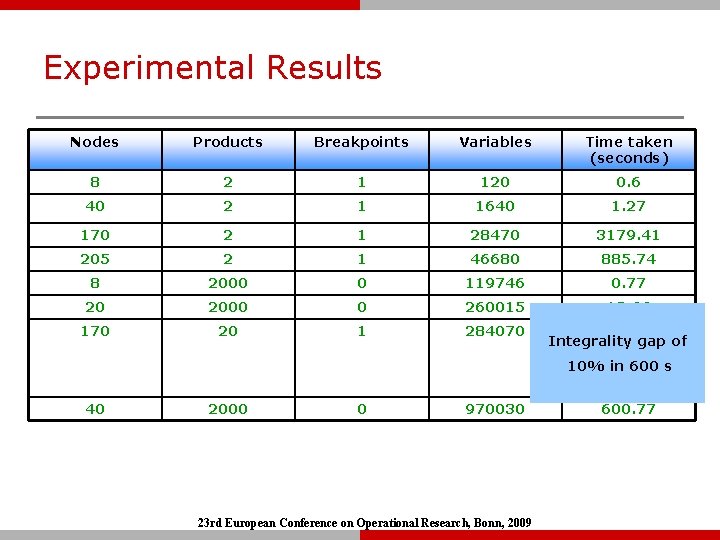
Experimental Results Nodes Products Breakpoints Variables Time taken (seconds) 8 2 1 120 0. 6 40 2 1 1640 1. 27 170 2 1 28470 3179. 41 205 2 1 46680 885. 74 8 2000 0 119746 0. 77 20 2000 0 260015 18. 66 170 20 1 284070 40 2000 0 970030 23 rd European Conference on Operational Research, Bonn, 2009 26957. 20 Integrality gap of (aborted at 10% in 600 gap s integrality 2%) 600. 77

Conclusions q Convenient and intuitive specification to handle uncertainty in supply chains. q Specification meaningful in economic terms and avoids adhoc assumptions about demand variations. q Correlations between different products incorporated, while retaining computational tractability. q Realistic costs with breakpoints lead to ILPs that are NPhard. However, a large number of medium scale problems with tens of thousands of variables are solvable in minutes on typical laptops. 23 rd European Conference on Operational Research, Bonn, 2009

Thank you Contact: Abhilasha Aswal: abhilasha_aswal@infosys. com G. N. Srinivasa Prasanna: gnsprasanna@iiitb. ac. in 23 rd European Conference on Operational Research, Bonn, 2009