New algorithms for exact and approximate text matching

New algorithms for exact and approximate text matching Szymon Grabowski Computer Engineering Dept. , Tech. Univ. of Łódź, Poland sgrabow@kis. p. lodz. pl habilitation thesis, Łódź 2011

String matching, what it’s all about There exist myriads of problems of the type: find a string (more generally: pattern) in a text. Applications: • text editors and ebook readers, • computational biology (DNA, proteins. . . ), • web search engines, • network traffic analysis and intrusion detection, • file systems, • AV scanners, • compression algorithms, • template matching (in images), • music retrieval (e. g. , query by humming handling), • . . 2

String (pattern) searching tasks • exact string matching (50+ research papers since mid-1970 s) • approximate search (several mismatches between P and a subsequence of T allowed) • multiple search • extended search (classes of characters, regular expressions, etc. ) • global measure of similarity between strings • 2 D search (in images) 3

Problems considered in thesis Exact online string matching (Chapter 1). Approximate online string matching (Chapter 2), incl. k-mismatches and Hamming distance. Matching with gaps (Chapter 3), incl. ( , )- and ( , , )-matching. Compressed pattern search (Chapter 4). Compressed full-text indexes (Chapter 5). 4

Chapter 1 Exact string matching Text T, pattern P, alphabet w – machine word size (in bits) n = |T|, m = |P|, = | | (alphabet size) Problem history: KMP, O(n) worst-case time (1977) BM, sublinear on avg (1977) Shift-Or, first bit-parallel alg, O(n) if m = O(w) (1989) BDM, optimal average-case time, i. e. O(n log (m) / m) (1994) BNDM, first bit-parallel alg avg-optimal if m = O(w) (2000) AOSO (Fredriksson & Grabowski, 2005) – very efficient bit-parallel alg, avg-optimal if m = O(w) 5

Chapter 1 Shift-Or (Baeza-Yates & Gonnet, 1992) D[ ] – state vector B[ ] – bit-vector for each alphabet symbol T = gcatcgcagagat P = gcaga Search phase, step-by-step (=column-by-column). Constant time per text character (if m = O(w)). 6

Chapter 1 Average Optimal Shift-Or (Fredriksson & Grabowski, 2005, 2009) We reduce O(n m / w ) time complexity of Shift-Or to O(n log (m) / min(m, w)) on average. This is average optimal for short patterns. The idea is to sample T in regular steps of q symbols and handle q matching subsequences in parallel. AOSO, main phase 7

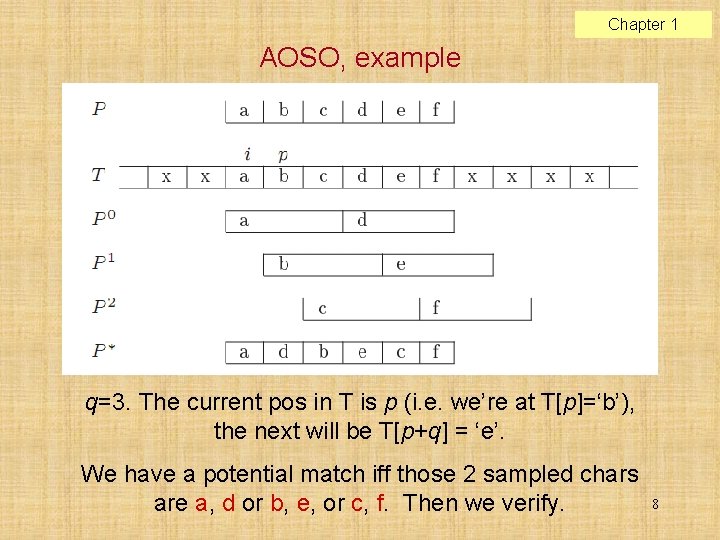
Chapter 1 AOSO, example q=3. The current pos in T is p (i. e. we’re at T[p]=‘b’), the next will be T[p+q] = ‘e’. We have a potential match iff those 2 sampled chars are a, d or b, e, or c, f. Then we verify. 8

Chapter 1 (F)AOSO technique results (NL, English) speeds [MB/s] Experiments on Intel Core 2 Duo (E 6850) 3. 0 GHz 9

Chapter 1 (F)AOSO technique results (DNA) speeds [MB/s] Experiments on Intel Core 2 Duo (E 6850) 3. 0 GHz 10

Chapter 1 AOSO algorithmic applications (Fredriksson & Grabowski, 2008, JDA). • approximate search under Hamming distance, • Average Optimal Aho–Corasick for multiple matching, • matching with swaps, • matching with all circular shifts. The AOSO algorithm (FG 05 paper) cited in: M. Kao (editor), Encyclopedia of Algorithms, Springer 2008, chapter Sequential Exact String Matching (by M. Crochemore & T. Lecroq). 11

Chapter 2 Approximate string matching Hamming distance between strings A and B: the number of positions j for which A[j] B[j]. E. g. , d. H(care, cord) = 2. Classic bit-parallel algorithm for searching under Hamming distance: Shift-Add (Baeza-Yates & Gonnet, 1992): it uses counters of O(log m) bits and works in O(n m log m / w ) time. For k-mismatches: in O(n m log k / w ) time. Grabowski and Fredriksson (2008): improved Shift-Add time complexity to O(n m / w ). 12

Chapter 2 Matryoshka counters (Grabowski & Fredriksson, 2008, IPL) In Shift-Add, the counters increment by at most 1 per text character. Matryoshka counters idea: use a number of nested counters, starting with O(1) bits in the lowest level, then flush lower-level counters only from time to time (periodically). Can work for many other string matching problems (FG’ 09, LATA conf. ). 13

Chapter 3 Matching with gaps A number of models assumes that the pattern characters may be separated by (variable-length) gaps in the matching text area. Popular models: ( , )-matching, ( , , )-matching. Applications: music information retrieval, protein analysis (after some model modification). -matching: a and b -match iff |a – b| . -matching: iff the gap between each pair of successive matching characters from T is . -matching: if the sum of deltas is . 14

Chapter 3 ( , )-matching in music information retrieval, example An excerpt from study Op. 25 Nr. 1 for Piano Solo by F. Chopin (first score). Melody P has a δ-approximate occurrence with α-bounded gaps in T, for δ ≥ 2 and α ≥ 5, indicated by the circled notes. Picture taken from Cantone et al. , New Efficient Bit-Parallel Algorithms for. . . , PSC’ 08 15

Chapter 3 Matching with gaps, recent development Fredriksson and Grabowski (2005– 2008): a number of new algorithms for those (and similar) problems proposed, competitive in theory and/or practice to the existing ones. Various preprocessing / search worst / avg case time trade-offs explored. Used techniques: • bit-parallelism, • sparse dynamic programming, • cut-off (for improving the average case), • bit-parallel simulation of NFA. 16

Chapter 4 Compressed pattern search (Amir & Benson, 1992) Input: text T’ available in a compressed form, pattern P. Output: report all occurrences of P in T (i. e. decompressed T’) without decompressing the whole T’. Word-based (W) and full-text (FT) schemes: W schemes will find: a rat sat on a mat, but NOT: rats’ population growth rate FT schemes will find all occurrences. 17

Chapter 4 q-gram based proposed FT algorithm (Fredriksson & Grabowski, 2006, IPL) Actually two search algorithms: very fast for “long” patterns (m 2 q– 1), somewhat slower and more complicated for short patterns (m < 2 q– 1). Compresses plain NL text to 45– 50% orig. size (worse than Ziv–Lempel but better than character based Huffman). Searching speed for long enough patterns is higher than in uncompressed text. 18

Chapter 4 Long pattern variant, an example Let P = nasty_bananas Let q = 3. Three alignments generated: 19

Chapter 4 The example, cont’d Encode the 3 -grams with ETDC byte code (Brisaboa et al. , 2003). The pattern alignments may turn into smth like: nas ty _ y_b ast sty an a b an an a _b a nas n an The resulting three sequences are input for a multiple exact string matching algorithm, potential matches must be verified. 20

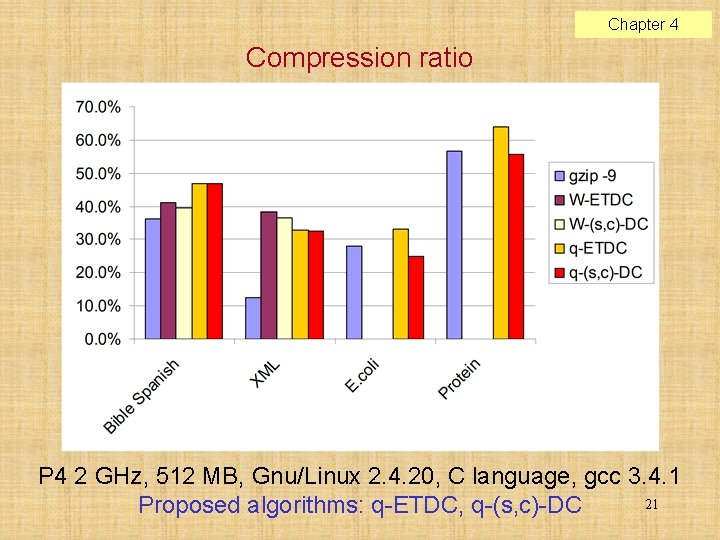
Chapter 4 Compression ratio P 4 2 GHz, 512 MB, Gnu/Linux 2. 4. 20, C language, gcc 3. 4. 1 21 Proposed algorithms: q-ETDC, q-(s, c)-DC

Chapter 4 Proteins, search times [s] Short patterns used for the test: random excerpts from text of length 2 q– 2. Long patterns in the test: minimum pat. lengths that produced compressed patterns of length at least 2. 22

Chapter 5 Compressed full-text indexes Full-text index: a structure over text T[1. . n] to find all subsequences of T in time sublinear in n. Compressed index: little extra space; the T itself may be eliminated and replaced by the compressed structure. FM-Huffman index (Grabowski et al. , 2004– 2006): a very simple variant from the FM index family (Ferragina & Manzini, 2000, 2005) with practical properties. A number of variants / tradeoffs proposed and tested. Main underlying ideas: • Burrows–Wheeler transform, • Huffman coding, • Fibonacci (Kautz-Zeckendorf) coding. 23

Chapter 5 Full-text indexes, past and present Past suffix tree (ST): powerful, flexible, but needs at least 10 n space suffix array (SA): 4 n space + 1 n text, otherwise quite practical Present compressed suffix array (CSA) (Grossi & Vitter, 2000; …) FM-index based on the BWT (Ferragina & Manzini, 2000, 2005) LZ-index based on the suffix tree with LZ 78 (Navarro, 2003; …) alphabet-friendly FM (Ferragina et al. , 2004, 2007) succinct ST (Sadakane, 2007; Russo et al. , 2008; …) self-indexed grammar-based compression (Claude & Navarro, 2009; Bille et al. , 2010) backward search in k-BWT (Petri et al. , 2011) 24

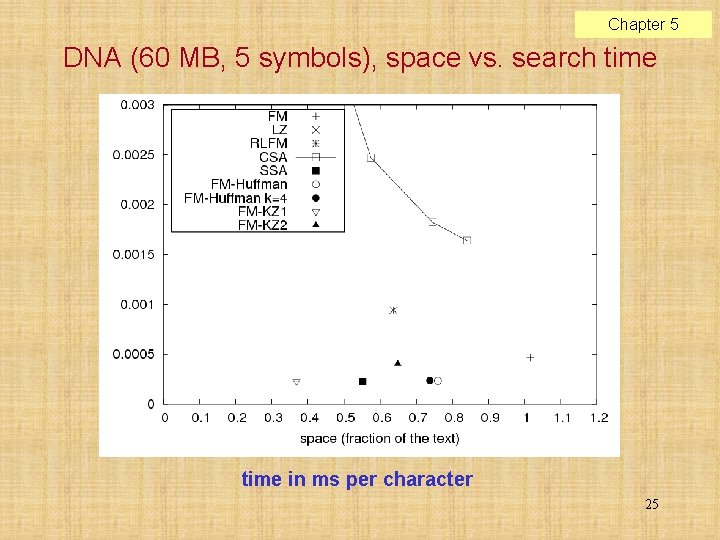
Chapter 5 DNA (60 MB, 5 symbols), space vs. search time in ms per character 25

Chapter 5 FM-Huffman / FM-KZ, complexities and summary Search time (count): O((H 0+1)m) avg search time. O(m log n) or O(m log ) worst-case search time. Space occupancy: less than 1. 44. . . * (H 0+1)n + o(H 0 n) bits. Pros and cons: • very simple and practical succinct index; • no dependence on the alphabet size; • among the fastest (but not the most succinct) compressed indexes; • worse “in theory” than some recent indexes (but simpler); • quite flexible. 26

Thesis summary Two new algorithmic techniques were proposed (regularly sparse text sampling and Matryoshka counters) with successful applications (in theory and/or practice) in well-known matching problems. Lots of new ideas and insight in the area of matching with gaps. In particular, we presented a new efficient bit-parallel algorithm handling negative gaps (application in bioinformatics). We proposed arguably one of the simplest, yet efficient, known algorithms for compressed matching (online and indexed). 27

28

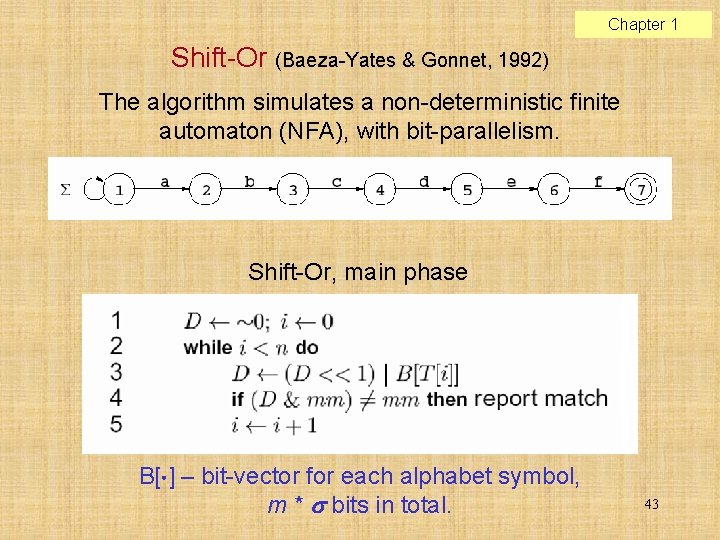
Chapter 1 Shift-Or (Baeza-Yates & Gonnet, 1992) The algorithm simulates a non-deterministic finite automaton (NFA), with bit-parallelism. Shift-Or, main phase B[ ] – bit-vector for each alphabet symbol, m * bits in total. 43