New Algorithms for 1 D Facility Location and

New Algorithms for 1 -D Facility Location and Path Equipartition Problems Danny Z. Chen and Haitao Wang University of Notre Dame Indiana, USA

Our Problems n General model facility location q q n n uniform k-median weighted k-median k-coverage linear model facility location L∞ path equipartition Ld path equipartition

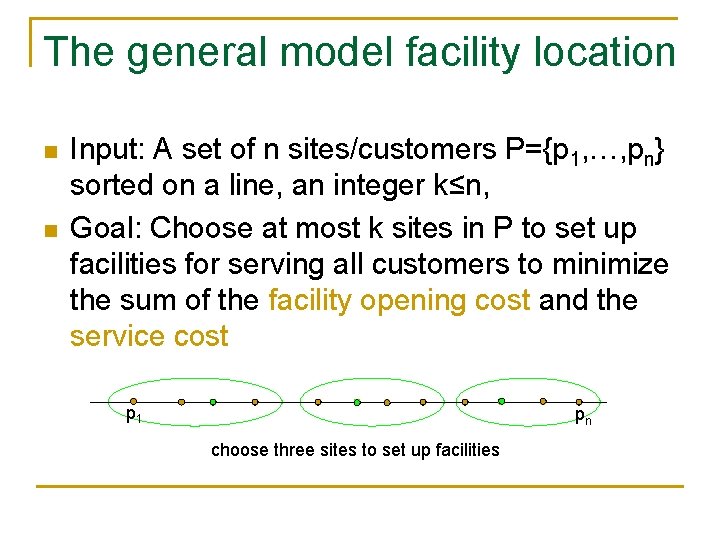
The general model facility location n n Input: A set of n sites/customers P={p 1, …, pn} sorted on a line, an integer k≤n, Goal: Choose at most k sites in P to set up facilities for serving all customers to minimize the sum of the facility opening cost and the service cost p 1 pn choose three sites to set up facilities

The general model facility location (cont. ) n n The facility opening cost q For each site pi, there is a cost ci for setting up a facility at pi The service cost q The distance of any two points pi and pj is their Euclidean distance on the line n q d(pi, pj)=|pi - pj| Each customer pj is associated with a service cost function fj(d) for a distance d such that: n n if we use a facility at pi to serve pj, the service cost for pj is fj(d(pi, pj)) fj(d) is a monotone increasing function with respect to d pj pi

The k-median n No facility opening cost q n ci=0, for each site pi The service cost functions are linear q For each site pj, fj(d)=aj * d n the uniform k-median q n all coefficients aj are the same the weighted k-median q the coefficients aj are not necessarily the same

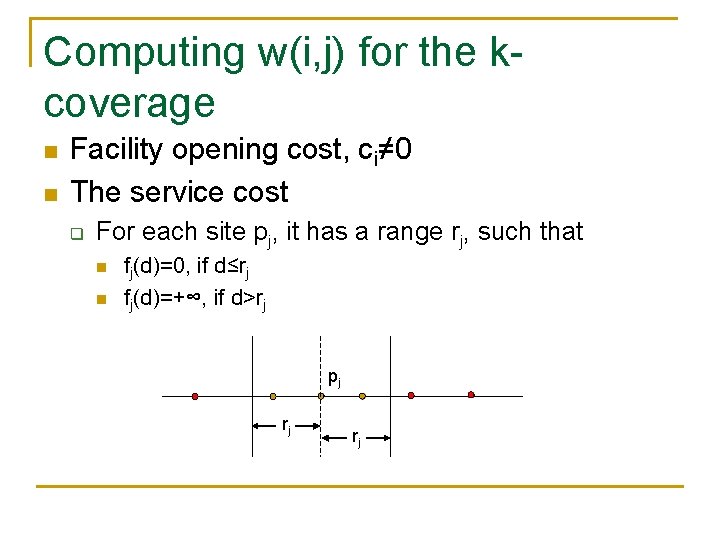
The k-coverage n The facility opening cost q n ci≠ 0 The service cost q For each site pj, it has a range rj, such that n n fj(d)=0, if d≤rj fj(d)=+∞, if d>rj pj rj rj

The linear model n The facility opening cost q n ci≠ 0 The service cost functions are linear q For each site pj, fj(d)=aj * d

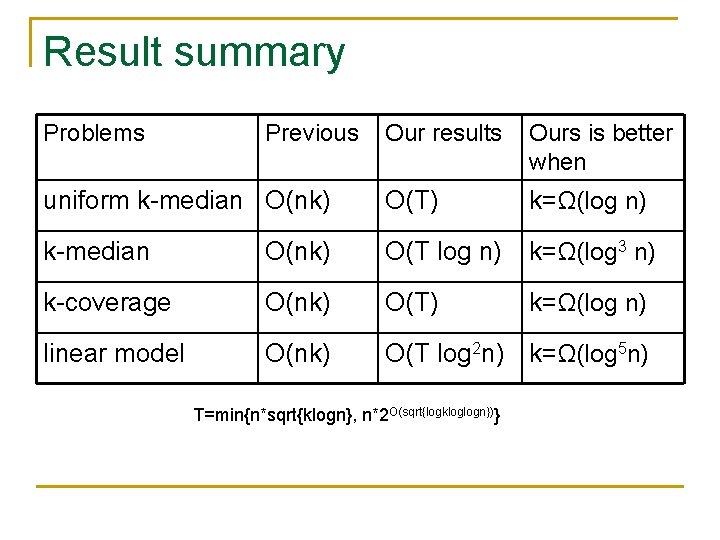
Previous work and our results n n n T=min{n*sqrt{klogn}, n*2 O(sqrt{logk loglogn})} The general model: O(n 2) time (Hassin and Tamir 91’) k-median q Previous work: O(nk) time (Hassin and Tamir 91’; Auletta, Parente, and Persiano 98’) n q Our result: n n n The uniform case: O(T) time, k=Ω(log n) The weighted case: O(T logn) time, k=Ω(log 3 n) k-coverage q q n Both uniform and weighted cases Previous work: O(nk) time (Hassin and Tamir 91’; van Hoesel and Wagelmans 07’) Our result: O(T) time, k=Ω(log n) Linear model q q Previous work: O(nk) time (Hassin and Tamir 91’) Our result: O(T log 2 n), k=Ω(log 5 n)

Result summary Problems Previous Our results Ours is better when uniform k-median O(nk) O(T) k=Ω(log n) k-median O(nk) O(T log n) k=Ω(log 3 n) k-coverage O(nk) O(T) k=Ω(log n) linear model O(nk) O(T log 2 n) k=Ω(log 5 n) T=min{n*sqrt{klogn}, n*2 O(sqrt{logkloglogn})}

Our techniques n Model the general model as the k-link shortest path problem q q Prove the concave Monge property holds Apply two k-link shortest path algorithms as the high-level scheme for our problem n n n O(n*sqrt{klogn}) time, Aggarwal, Schieber, and Tokuyama, 94’ O(n*2 O(sqrt{logk loglogn})) time, Schieber 98’ The problem modeling looks natural q Previous work does not use it

Our techniques (cont. ) n The concave Monge property in this problem modeling is not obvious q q q Monge property is used in the previous work but only on the service cost The Monge property in our problem modeling also involves the facility opening cost There is an obvious monotone property on the service cost but not on the facility opening cost

The k-link shortest path problem n n n Input: A weighted DAG G with vertices v 1, …, vn, and an integer k, 1≤k≤n Output: Finding a path of k edges from v 1 to vn such that the sum of the weights of the edges in the path is minimized Concave Monge property: q For any i and j with 1<i+1<j<n, n v 1 w(i, j)+w(i+1, j+1) ≤ w(i, j+1)+w(i+1, j) vi vi+1 vj vj+1 vn

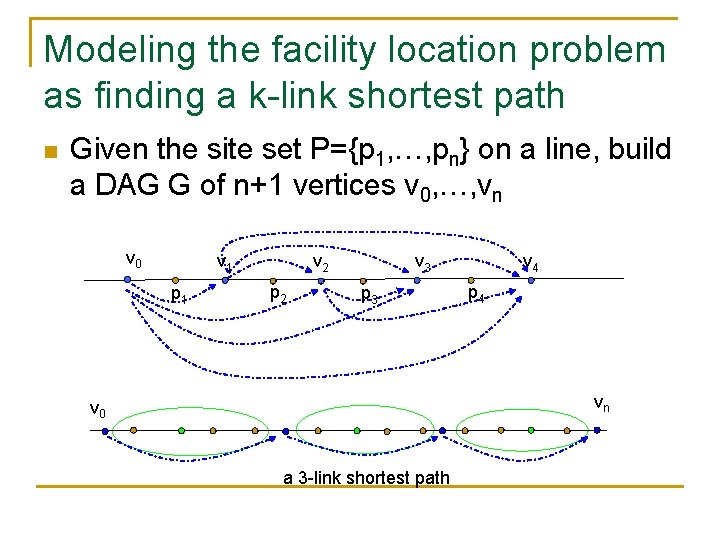
Modeling the facility location problem as finding a k-link shortest path n Given the site set P={p 1, …, pn} on a line, build a DAG G of n+1 vertices v 0, …, vn v 0 v 1 p 1 v 2 p 2 v 3 p 3 v 4 p 4 vn v 0 a 3 -link shortest path

Model the facility location problem as the k-link shortest path (cont. ) n n The weight w(i, j) of each edge from vi to vj is the minimum cost of opening one facility and serving all customers in the group defined by the edge w(i, j) has two parts q q n The cost of opening one facility The total service cost We prove that the concave Monge property holds on w(i, j) vi vj

Proving the concave Monge property on w(i, j) n An observation: The positions of facilities satisfy a monotone property wij+1 vi vi vj vj+1

The algorithms n High-level scheme: q n The computational components q n q T: the k-link shortest path algorithms W: time for computing each w(i, j) k-median and k-coverage q n Compute the edge weights w(i, j) Running time O(T*W) q n Apply the k-link shortest path algorithms Design data structures to answer w(i, j) queries The linear model q Modify the k-link shortest path algorithms

Computing w(i, j) for the k-median n n No facility opening cost, ci=0 The service cost functions are linear q n The uniform case q q n For each site pj, fj(d)=aj * d n the uniform k-median: all coefficients aj are the same The facility is set up at the median site in the group O(1) time (O(n) time preprocessing) The weighted case q q The facility is the weighted median site in the group O(log n) time by binary search (O(n) time preprocessing) vj vi wij

Computing w(i, j) for the kcoverage n n Facility opening cost, ci≠ 0 The service cost q For each site pj, it has a range rj, such that n n fj(d)=0, if d≤rj fj(d)=+∞, if d>rj pj rj rj

Computing w(i, j) for the k-coverage (cont. ) n Reduce querying w(i, j) to the following points in intervals query problem q q Given n points p 1, …, pn sorted on a line, each pi is associated with a cost ci and an interval Ii that contains pi Query: For each query (i, j) with i≤j, report a point pm with the smallest cost such that i ≤m≤ j and pm is contained in all intervals from Ii to Ij

Computing w(i, j) for the k-coverage (cont. ) n Reduce querying w(i, j) to the following points in intervals query problem q q Given n points p 1, …, pn sorted on a line, each pi is associated with a cost ci and an interval Ii that contains pi Query: For each query (i, j) with i≤j, report a point pm with the smallest cost such that i ≤m≤ j and pm is contained in all intervals from Ii to Ij j i

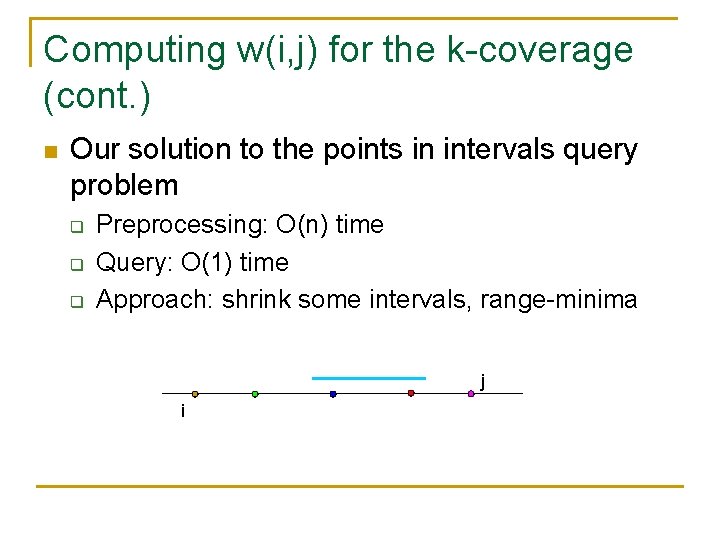
Computing w(i, j) for the k-coverage (cont. ) n Our solution to the points in intervals query problem q q q Preprocessing: O(n) time Query: O(1) time Approach: shrink some intervals, range-minima j i

Computing w(i, j) for the linear model n n The facility opening cost, ci≠ 0 The service cost functions are linear q n n n We do not build a query data structure An observation: Compute a special group of O(n) edge weights in O(n log n) time Modify the two k-link shortest path algorithms q n For each site pj, fj(d)=aj * d Use a new row-minima algorithm instead of the linear time SMAWK algorithm Overall running time: O(T log 2 n)

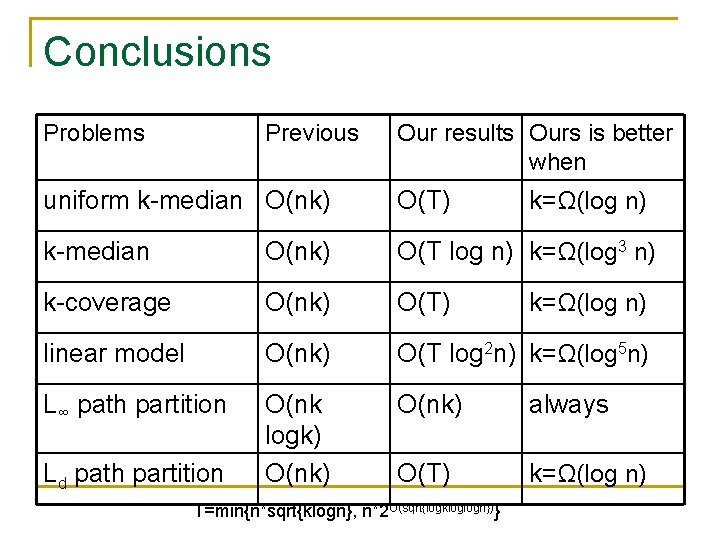
Conclusions Problems Previous Our results Ours is better when uniform k-median O(nk) O(T) k-median O(nk) O(T log n) k=Ω(log 3 n) k-coverage O(nk) O(T) linear model O(nk) O(T log 2 n) k=Ω(log 5 n) L∞ path partition O(nk logk) O(nk) always O(T) k=Ω(log n) Ld path partition T=min{n*sqrt{klogn}, n*2 O(sqrt{logkloglogn})} k=Ω(log n)

Thank you