Neutron interaction with matter 1 Introduction 2 Elastic

Neutron interaction with matter 1) Introduction 2) Elastic scattering of neutrons 3) Inelastic scattering of neutrons 4) Neutron capture 5) Other nuclear reactions 6) Spallation reactions, hadron shower Important cross sections of nuclear interactions Mostly neutron loses only part of energy

Introduction Neutron has not electric charge → interaction only by strong nuclear interaction Magnetic moment of neutron → interaction by electromagnetic interaction, mostly negligible influence Different energy ranges of neutrons: Ultracold: E < 10 -6 e. V Cold and very cold: E = (10 -6 e. V – 0, 0005 e. V) Thermal neutrons – (0, 002 e. V – 0, 5 e. V) neutrons are in thermal equilibrium with neighborhood, Maxwell distribution of velocities, for 20 o. C is the most probable velocity v = 2200 m/s → E = 0, 0253 e. V Epithermál neutrons and resonance neutrons: E = (0, 5 e. V – 1000 e. V) Cadmium threshold: ~ 0, 5 e. V - with higher energy pass through 1 mm of Cd Slow neutrons: E < 1 ke. V Neutrons with middle energies: E = (1 ke. V – 500 ke. V) Fast neutrons: E = (0, 5 Me. V – 20 Me. V) Neutrons with high energies: E = (20 Me. V – 100 Me. V) Relativistic neutrons: 0, 1 – 10 Ge. V Ultrarelativistic neutrons: E > 10 Ge. V

Elastic scattering of neutrons Most frequent process used for kinetic energy decreasing (moderation) of neutrons Moderation – process of set of independent elastic collisions of neutron on nuclei Usage of nucleus reflected during scattering for neutron energy determination Maximal transferred energy (nonrelativistic case of head-head collision): MCL: pn 0 = p. A - pn ECL: En 0 KIN = EAKIN + En. KIN pn 02/2 mn = p. A 2/2 m. A + pn 2/2 mn MCL: pn 2 = p. A 2 – 2 p. Apn 0 + pn 02 m. Apn 2 = ECL: m. Apn 2 = - mnp. A 2 m. Ap. A 2 – 2 m. Apn 0 + m. Apn 02 We subtract equation: 0 = m. Ap. A 2 + mnp. A 2 – 2 m. Apn 0 m. Ap. A + mnp. A = 2 m. Apn 0 The heavier nucleus the lower energy can neutron transferred to it: Nucleon number A

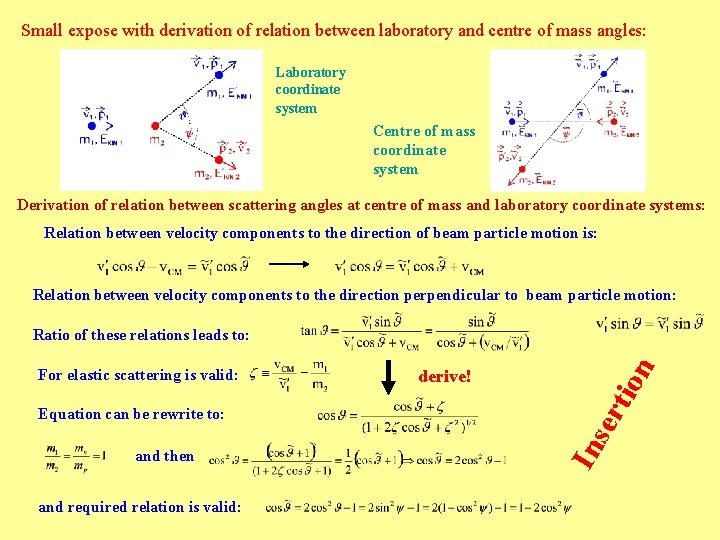
Usage of hydrogen (θ – neutron scattering angle, ψ – proton reflection angle) mp = mn: pn = pn 0·cosθ En = En 0·cos 2θ pn = pn 0·sinψ En = En 0 ·sin 2ψ ψ = π/2 -θ pp = pn 0·sinθ Ep = En 0·sin 2θ pp = pn 0·cosψ Ep = En 0·cos 2ψ For nucleus: Reflection angle φ Elastic scattering: in our case particle 1 – neutron particle 2 – proton, generally nucleus Dependency of energy transferred to proton on reflected angle

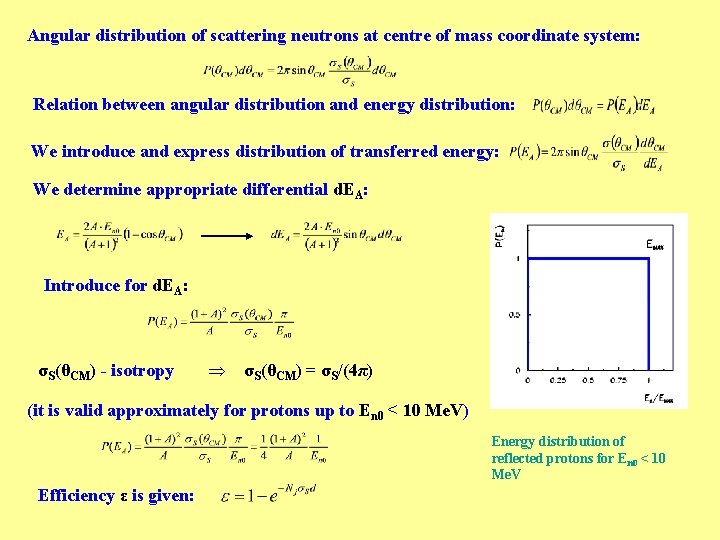
Small expose with derivation of relation between laboratory and centre of mass angles: Laboratory coordinate system Centre of mass coordinate system Derivation of relation between scattering angles at centre of mass and laboratory coordinate systems: Relation between velocity components to the direction of beam particle motion is: Relation between velocity components to the direction perpendicular to beam particle motion: and then and required relation is valid: tio ser Equation can be rewrite to: derive! In For elastic scattering is valid: n Ratio of these relations leads to:

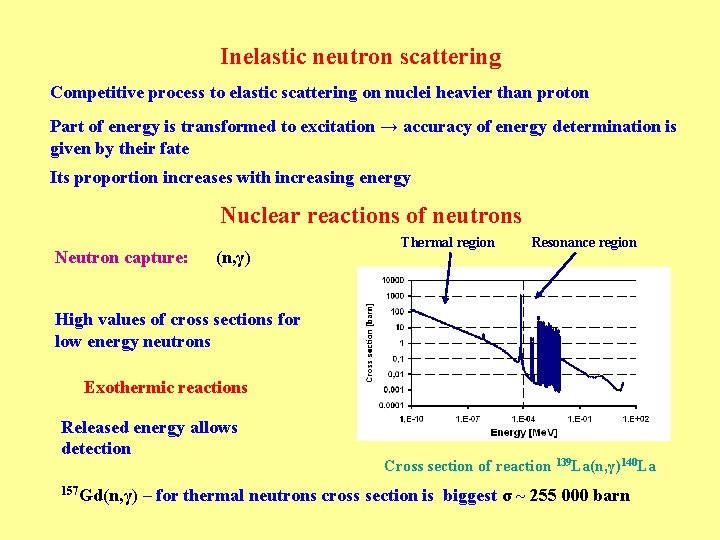
Angular distribution of scattering neutrons at centre of mass coordinate system: Relation between angular distribution and energy distribution: We introduce and express distribution of transferred energy: We determine appropriate differential d. EA: Introduce for d. EA: σS(θCM) - isotropy σS(θCM) = σS/(4π) (it is valid approximately for protons up to En 0 < 10 Me. V) Energy distribution of reflected protons for En 0 < 10 Me. V Efficiency ε is given:

Coherent scattering – diffraction on lattice Magnitude of energy neither momentum and wave length of neutrons are not changed Diffraction of neutrons on crystal lattice is used Mentioning: Bragg law: n·λ = 2 d·sin Θ En << mnc 2 = 0, 0288 e. V½∙nm for En in [e. V] Lattice constants are in the order 0, 1 – 1 nm → Neutron energy in the orders of me. V up to e. V E [e. V] 0, 001 0, 005 0, 01 0, 1 1 10 1000 λ [nm] 0, 91 0, 41 0, 29 0, 091 0, 029 0, 0091 0, 0029 0, 00091

Inelastic neutron scattering Competitive process to elastic scattering on nuclei heavier than proton Part of energy is transformed to excitation → accuracy of energy determination is given by their fate Its proportion increases with increasing energy Nuclear reactions of neutrons Neutron capture: (n, γ) Thermal region Resonance region High values of cross sections for low energy neutrons Exothermic reactions Released energy allows detection Cross section of reaction 139 La(n, γ)140 La 157 Gd(n, γ) – for thermal neutrons cross section is biggest σ ~ 255 000 barn

Cross section [barn] Threshold reactions Bi(n, Xn)Bi Examples of threshold reactions: 197 Au(n, 2 n)196 Au 197 Au(n, 4 n)194 Au 27 Al(n, α)24 Na Energy [Me. V] Cross section [barn] Reaction (n, 2 n), (n, 3 n), . . . Endothermic (threshold) reactions Energy [Me. V] Reactions (n, d), (n, t), (n, α). . . Reactions used for detection of low energy neutrons (exoenergy): (two particle decay of compound nucleus at rest, nonrelativistic approximation) EN + E P = Q m. Nv. N = m. Pv. P → 10 B(n, α)7 Li Q = 2, 792 and 2, 310 Me. V, Eα = Me. V, ELi = Me. V σth = 3840 b 1/v up to 1 ke. V 6 Li(n, α)3 H Q = 4, 78 Me. V, E 3 He(n, p)3 H α = 2, 05 Me. V, EH = 2, 73 Me. V σth = 940 b 1/v up to 10 ke. V Q = 0, 764 Me. V, Ep = 0, 573 Me. V, EH = 0, 191 Me. V σth = 5330 b 1/v up to 2 ke. V Reactions used for detection of fast neutrons – threshold reactions

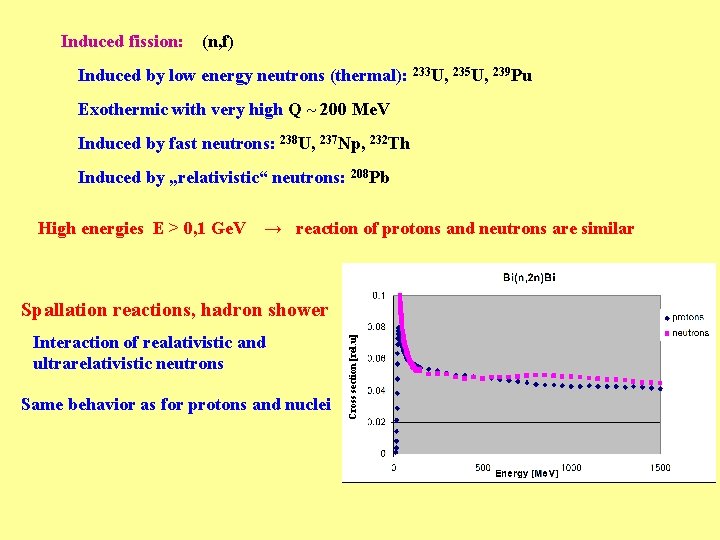
Induced fission: (n, f) Induced by low energy neutrons (thermal): 233 U, 235 U, 239 Pu Exothermic with very high Q ~ 200 Me. V Induced by fast neutrons: 238 U, 237 Np, 232 Th Induced by „relativistic“ neutrons: 208 Pb High energies E > 0, 1 Ge. V → reaction of protons and neutrons are similar Interaction of realativistic and ultrarelativistic neutrons Same behavior as for protons and nuclei Cross section [rel. u] Spallation reactions, hadron shower