Neural networks Reading Ch 20 Sec 5 AIMA

Neural networks Reading: Ch. 20, Sec. 5, AIMA 2 nd Ed Rutgers CS 440, Fall 2003

Outline • • • Human learning, brain, neurons Artificial neural networks Perceptron Learning in NNs Multi-layer NNs Hopfield networks Rutgers CS 440, Fall 2003

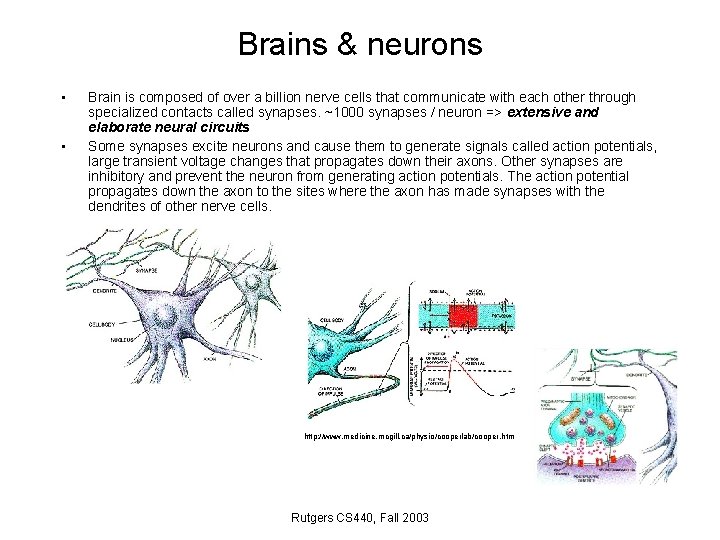
Brains & neurons • • Brain is composed of over a billion nerve cells that communicate with each other through specialized contacts called synapses. ~1000 synapses / neuron => extensive and elaborate neural circuits Some synapses excite neurons and cause them to generate signals called action potentials, large transient voltage changes that propagates down their axons. Other synapses are inhibitory and prevent the neuron from generating action potentials. The action potential propagates down the axon to the sites where the axon has made synapses with the dendrites of other nerve cells. http: //www. medicine. mcgill. ca/physio/cooperlab/cooper. htm Rutgers CS 440, Fall 2003

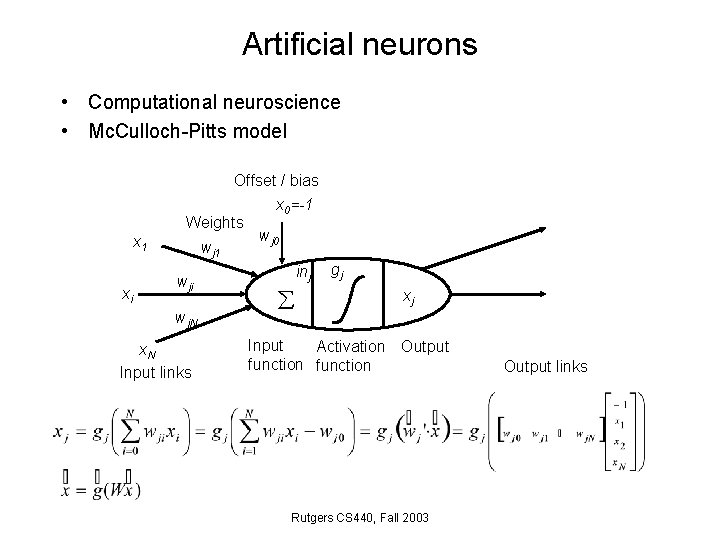
Artificial neurons • Computational neuroscience • Mc. Culloch-Pitts model x 1 xi Offset / bias x 0=-1 Weights wj 0 wj 1 wji wj. N x. N Input links inj gj xj Input Activation Output function Rutgers CS 440, Fall 2003 Output links

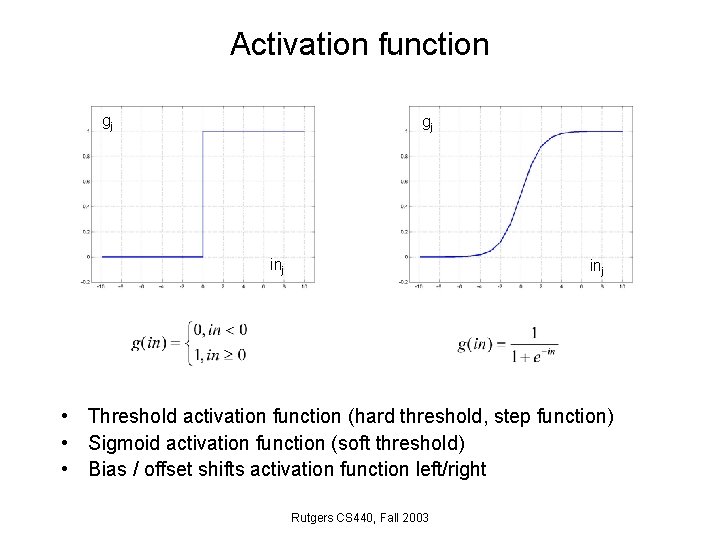
Activation function gj gj inj • Threshold activation function (hard threshold, step function) • Sigmoid activation function (soft threshold) • Bias / offset shifts activation function left/right Rutgers CS 440, Fall 2003

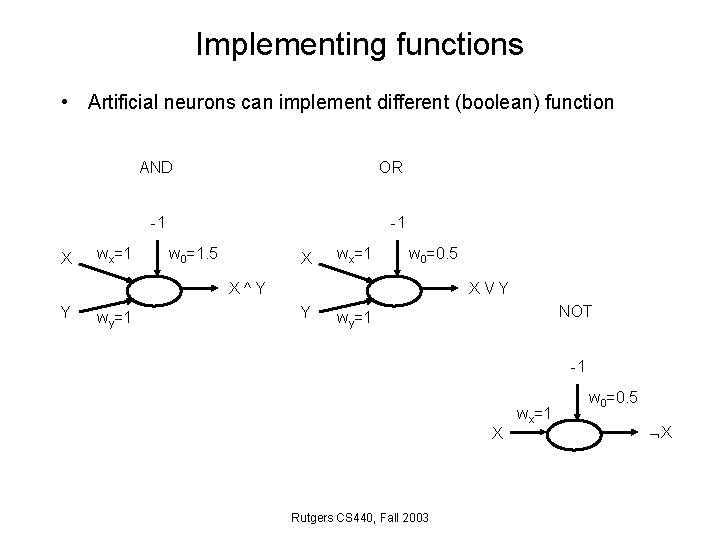
Implementing functions • Artificial neurons can implement different (boolean) function AND OR -1 X wx=1 -1 w 0=1. 5 X wx=1 w 0=0. 5 X^Y Y wy=1 XVY Y NOT wy=1 -1 X Rutgers CS 440, Fall 2003 wx=1 w 0=0. 5 X

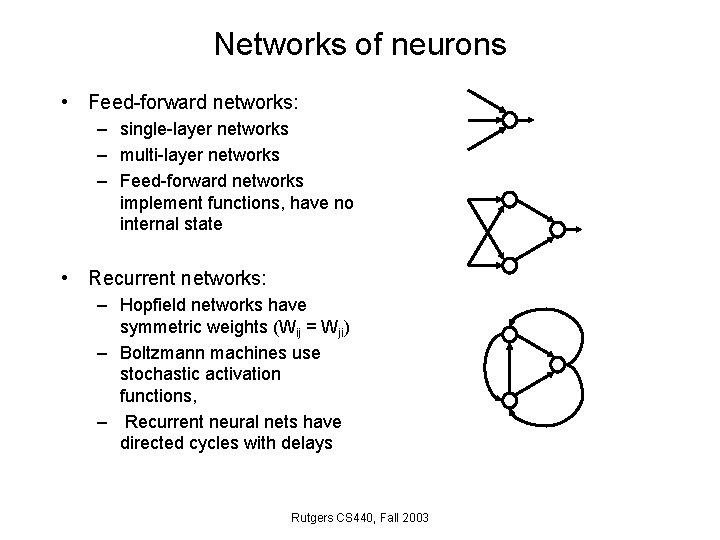
Networks of neurons • Feed-forward networks: – single-layer networks – multi-layer networks – Feed-forward networks implement functions, have no internal state • Recurrent networks: – Hopfield networks have symmetric weights (Wij = Wji) – Boltzmann machines use stochastic activation functions, – Recurrent neural nets have directed cycles with delays Rutgers CS 440, Fall 2003

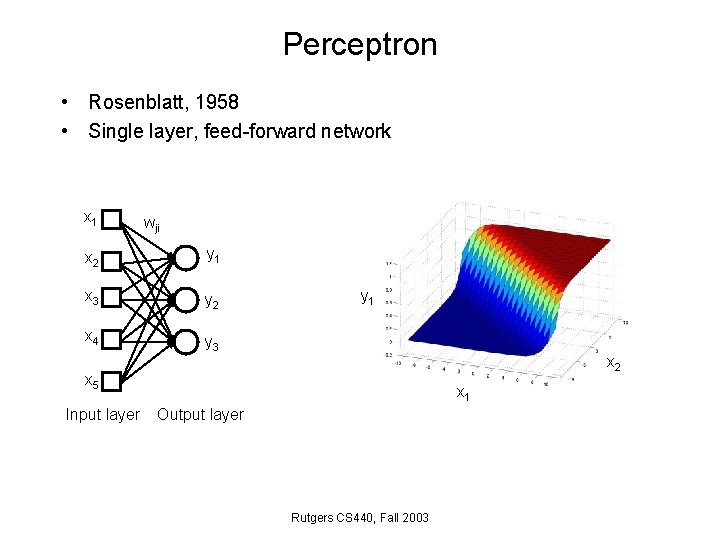
Perceptron • Rosenblatt, 1958 • Single layer, feed-forward network x 1 wji x 2 y 1 x 3 y 2 x 4 y 3 y 1 x 2 x 5 Input layer x 1 Output layer Rutgers CS 440, Fall 2003

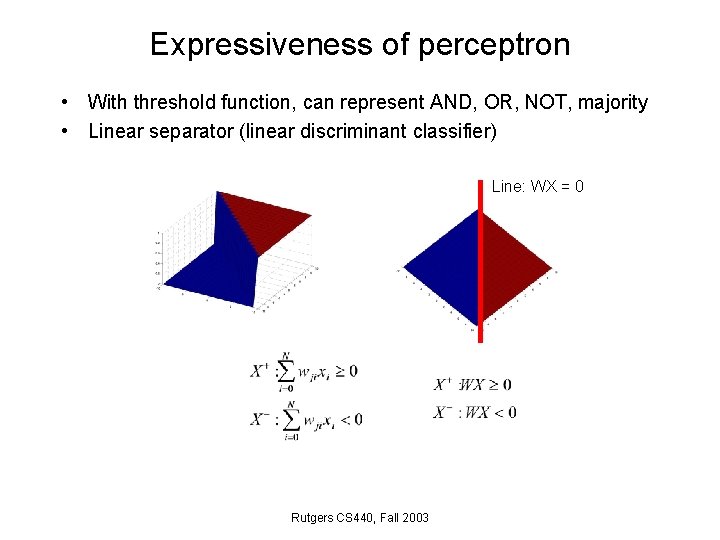
Expressiveness of perceptron • With threshold function, can represent AND, OR, NOT, majority • Linear separator (linear discriminant classifier) Line: WX = 0 Rutgers CS 440, Fall 2003

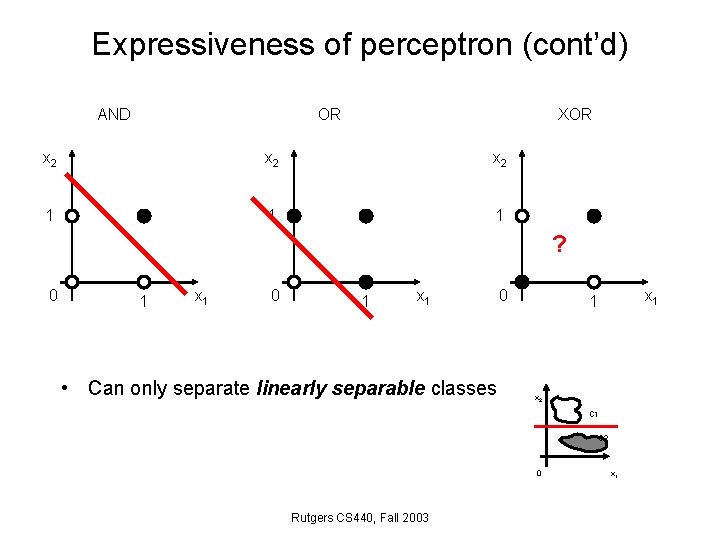
Expressiveness of perceptron (cont’d) AND OR XOR x 2 x 2 1 1 1 ? 0 1 x 1 • Can only separate linearly separable classes 0 x 1 1 x 2 C 1 C 2 0 Rutgers CS 440, Fall 2003 x 1

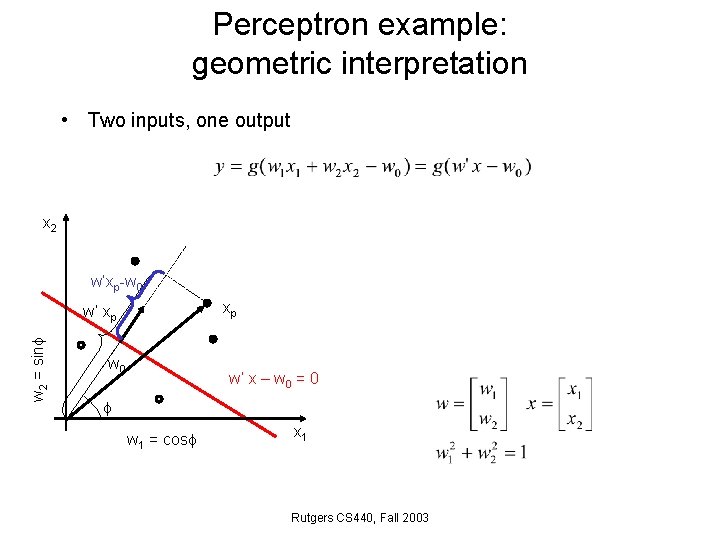
Perceptron example: geometric interpretation • Two inputs, one output x 2 w’xp-w 0 xp w 2 = sin w’ xp w 0 w’ x – w 0 = 0 w 1 = cos x 1 Rutgers CS 440, Fall 2003

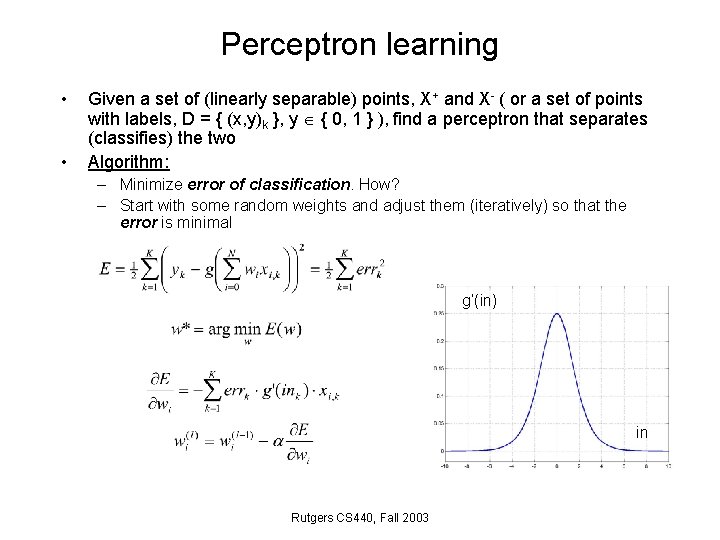
Perceptron learning • • Given a set of (linearly separable) points, X+ and X- ( or a set of points with labels, D = { (x, y)k }, y { 0, 1 } ), find a perceptron that separates (classifies) the two Algorithm: – Minimize error of classification. How? – Start with some random weights and adjust them (iteratively) so that the error is minimal g’(in) in Rutgers CS 440, Fall 2003

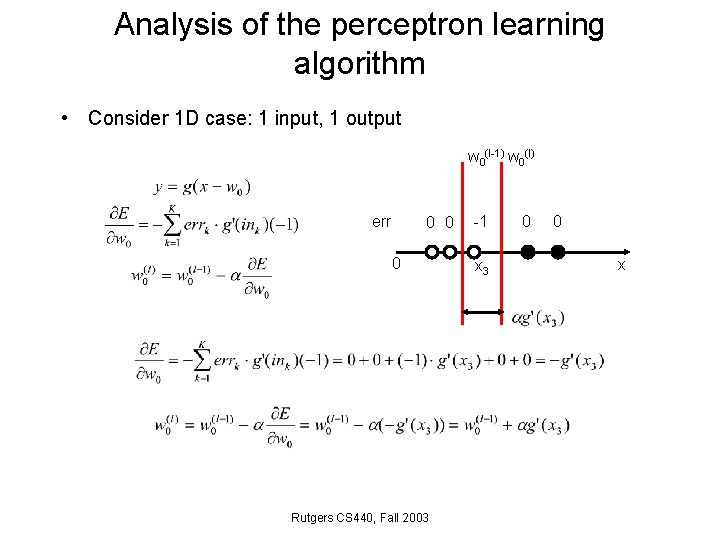
Analysis of the perceptron learning algorithm • Consider 1 D case: 1 input, 1 output w 0(l-1) w 0(l) err 0 0 0 Rutgers CS 440, Fall 2003 -1 x 3 0 0 x

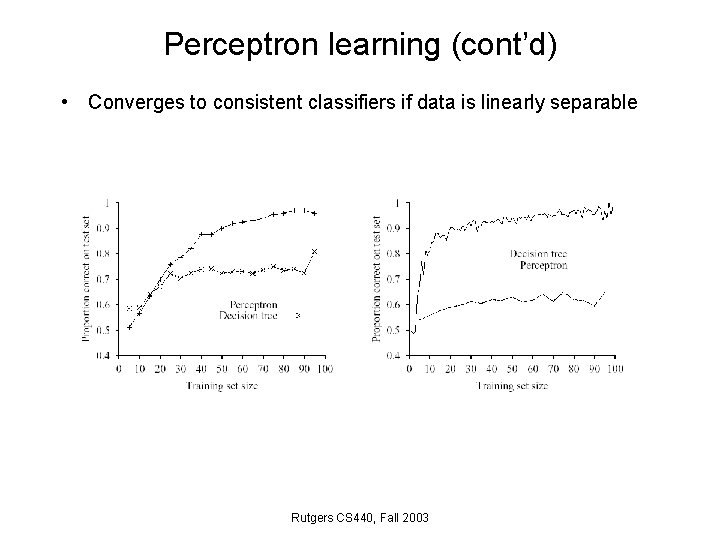
Perceptron learning (cont’d) • Converges to consistent classifiers if data is linearly separable Rutgers CS 440, Fall 2003

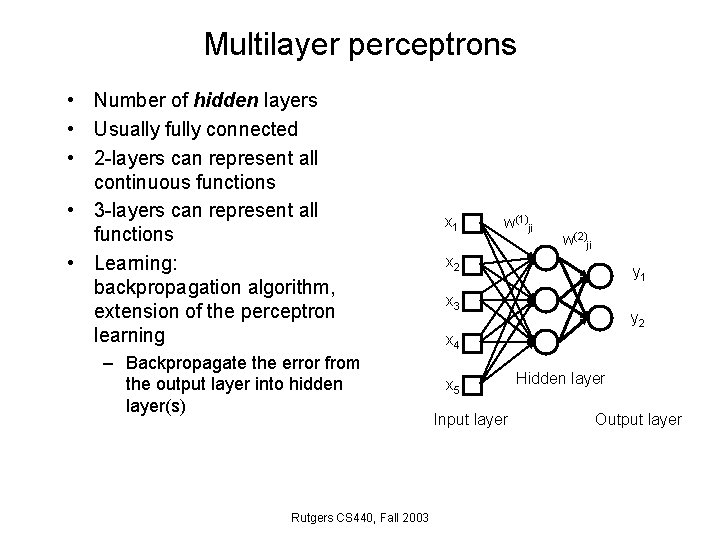
Multilayer perceptrons • Number of hidden layers • Usually fully connected • 2 -layers can represent all continuous functions • 3 -layers can represent all functions • Learning: backpropagation algorithm, extension of the perceptron learning – Backpropagate the error from the output layer into hidden layer(s) Rutgers CS 440, Fall 2003 x 1 w(1)ji w(2)ji x 2 y 1 x 3 y 2 x 4 x 5 Input layer Hidden layer Output layer

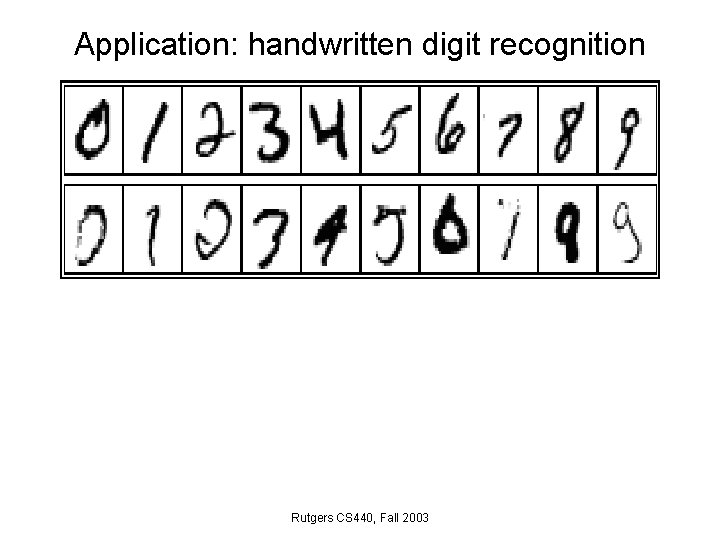
Application: handwritten digit recognition Rutgers CS 440, Fall 2003

Probabilistic interpretation • Two classes, X+ and X-, elements of which are distributed randomly according to some densities p+(x) and p-(x) Classes have prior probabilities p+ and p. Given an element x decide which class it belongs to. • • X+ X- • Output of NN is the posterior probability of a data class Rutgers CS 440, Fall 2003

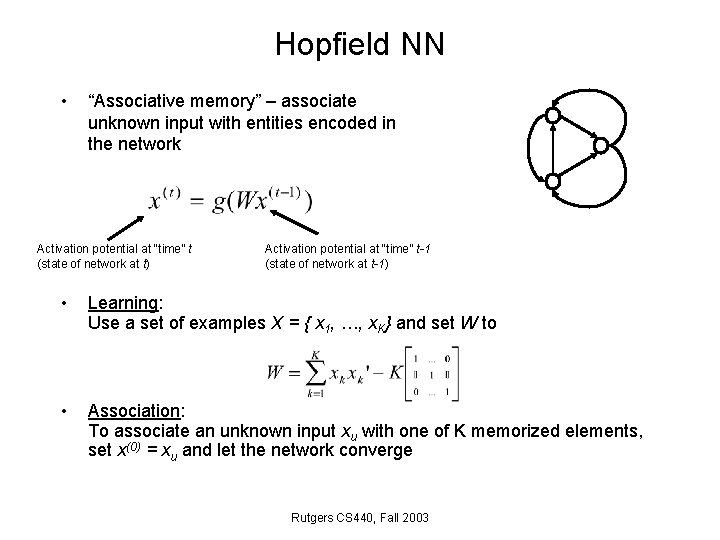
Hopfield NN • “Associative memory” – associate unknown input with entities encoded in the network Activation potential at “time” t (state of network at t) Activation potential at “time” t-1 (state of network at t-1) • Learning: Use a set of examples X = { x 1, …, x. K} and set W to • Association: To associate an unknown input xu with one of K memorized elements, set x(0) = xu and let the network converge Rutgers CS 440, Fall 2003

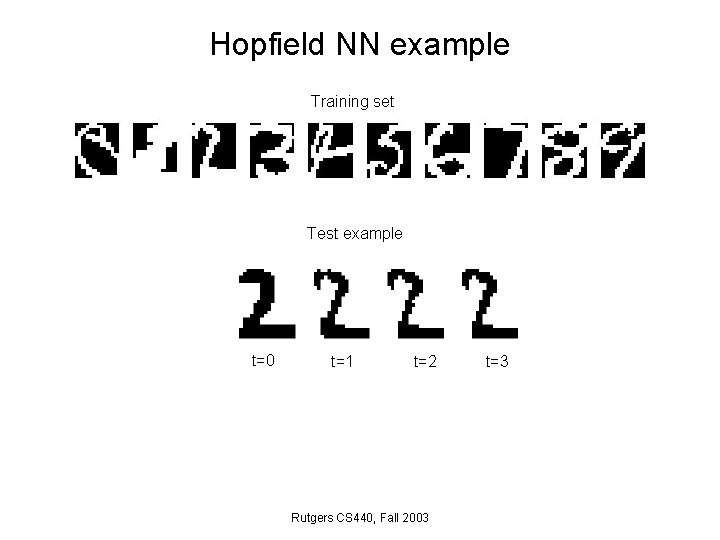
Hopfield NN example Training set Test example t=0 t=1 t=2 Rutgers CS 440, Fall 2003 t=3