Neural Networks Capabilities and Examples L Manevitz Computer

Neural Networks: Capabilities and Examples L. Manevitz Computer Science Department HIACS Research Center University of Haifa L. Manevitz U. Haifa 1

What Are Neural Networks? What Are They Good for? How Do We Use Them? • Definitions and some history • Basics – Basic Algorithms – Examples • Recent Examples • Future Directions L. Manevitz U. Haifa 2

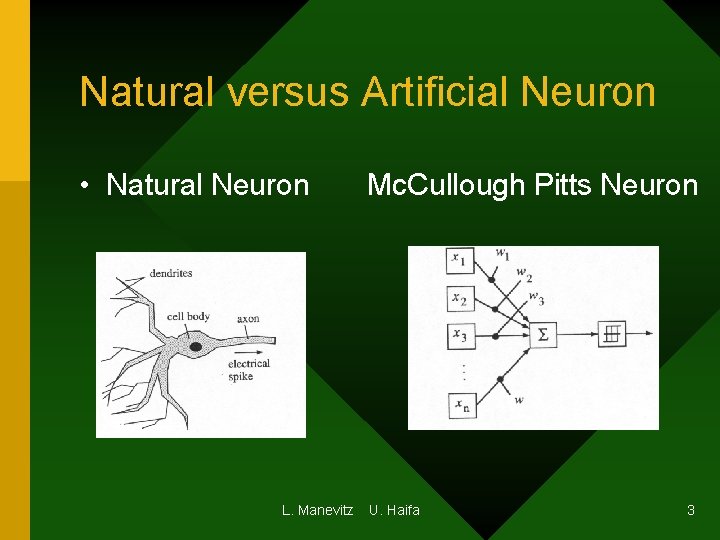
Natural versus Artificial Neuron • Natural Neuron L. Manevitz Mc. Cullough Pitts Neuron U. Haifa 3

Definitions and History • Mc. Cullough –Pitts Neuron • Perceptron • Adaline • Linear Separability • Multi-Level Neurons • Neurons with Loops L. Manevitz U. Haifa 4

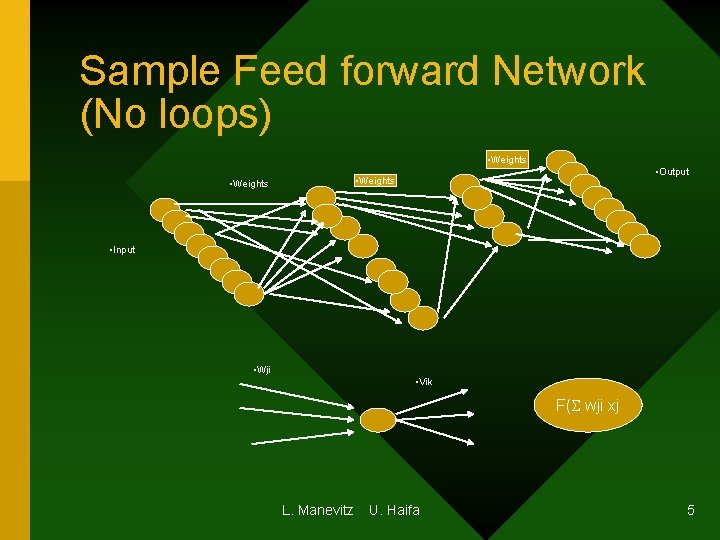
Sample Feed forward Network (No loops) • Weights • Output • Weights • Input • Wji • Vik F(S wji xj L. Manevitz U. Haifa 5

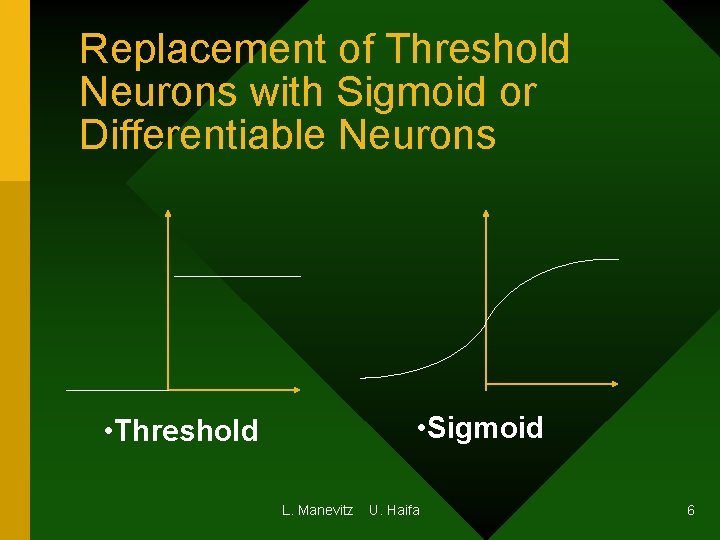
Replacement of Threshold Neurons with Sigmoid or Differentiable Neurons • Sigmoid • Threshold L. Manevitz U. Haifa 6

Reason for Explosion of Interest • Two co-incident affects (around 1985 – 87) – (Re-)discovery of mathematical tools and algorithms for handling large networks – Availability (hurray for Intel and company!) of sufficient computing power to make experiments practical. L. Manevitz U. Haifa 7

Some Properties of NNs • Universal: Can represent and accomplish any task. • Uniform: “Programming” is changing weights • Automatic: Algorithms for Automatic Programming; Learning L. Manevitz U. Haifa 8

Networks are Universal • All logical functions represented by three level (non-loop) network (Mc. Cullough-Pitts) • All continuous (and more) functions represente by three level feed-forward networks (Cybenko al. ) • Networks can self organize (without teacher). • Networks serve as associative memories L. Manevitz U. Haifa 9

Universality • Mc. Cullough-Pitts: Adaptive Logic Gates; can represent any logic function • Cybenko: Any continuous function representable by three-level NN. L. Manevitz U. Haifa 10

Networks can “LEARN” and Generalize (Algorithms) • One Neuron (Perceptron and Adaline) Very popular in 1960 s – early 70 s – Limited by representability (only linearly separable • Feed forward networks (Back Propagation) – Currently most popular network (1987 –now) • Kohonen self-Organizing Network (1980 s – now)(loops) • Attractor Networks (loops) L. Manevitz U. Haifa 11

Learnability (Automatic Programming) • One neuron: Perceptron and Adaline algorithms (Rosenblatt and Widrow-Hoff) (1960 s –now) Feed forward Networks: Backpropagation (1987 – now) Associative Memories and Looped Networks (“Attractors”) (1990 s – now) L. Manevitz U. Haifa 12

Generalizability • Typically train a network on a sample set of examples • Use it on general class • Training can be slow; but execution is fast. L. Manevitz U. Haifa 13

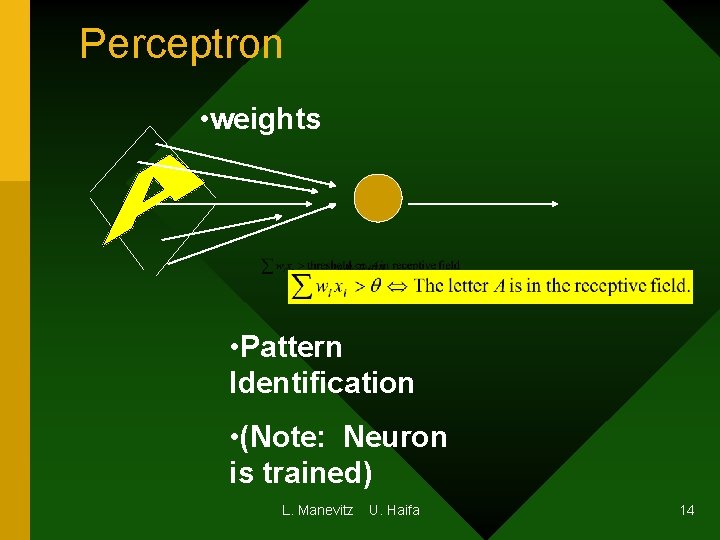
Perceptron • weights • Pattern Identification • (Note: Neuron is trained) L. Manevitz U. Haifa 14

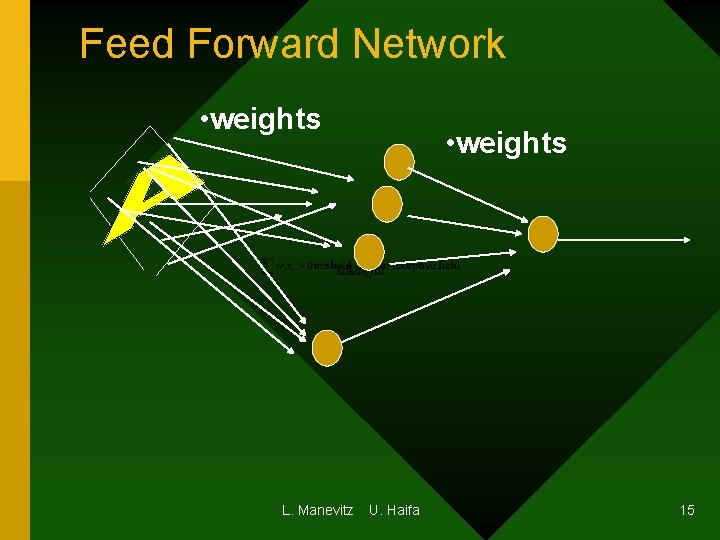
Feed Forward Network • weights L. Manevitz • weights U. Haifa 15

Classical Applications (1986 – 1997) • “Net Talk” : text to speech • ZIPcodes: handwriting analysis • Glovetalk: Sign Language to speech • Data and Picture Compression: “Bottleneck” • Steering of Automobile (up to 55 m. p. h) • Market Predictions • Associative Memories • Cognitive Modeling: (especially reading, …) L. Manevitz U. (Finnish) Haifa • Phonetic Typewriter 16

Neural Network • Once the architecture is fixed; the only free parameters are the weights • Thus Uniform Programming • Potentially Automatic Programming • Search for Learning Algorithms L. Manevitz U. Haifa 17

Programming: Just find the weights! • AUTOMATIC PROGRAMMING • One Neuron: Perceptron or Adaline • Multi-Level: Gradient Descent on Continuous Neuron (Sigmoid instead of step function). L. Manevitz U. Haifa 18

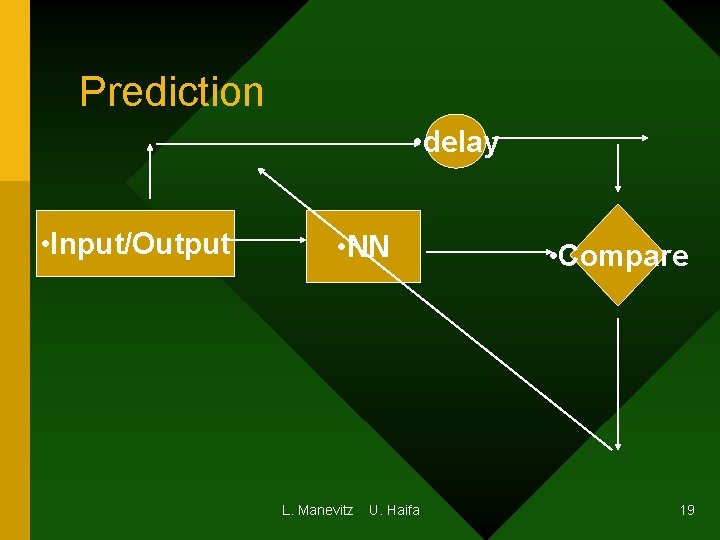
Prediction • delay • Input/Output • NN L. Manevitz U. Haifa • Compare 19

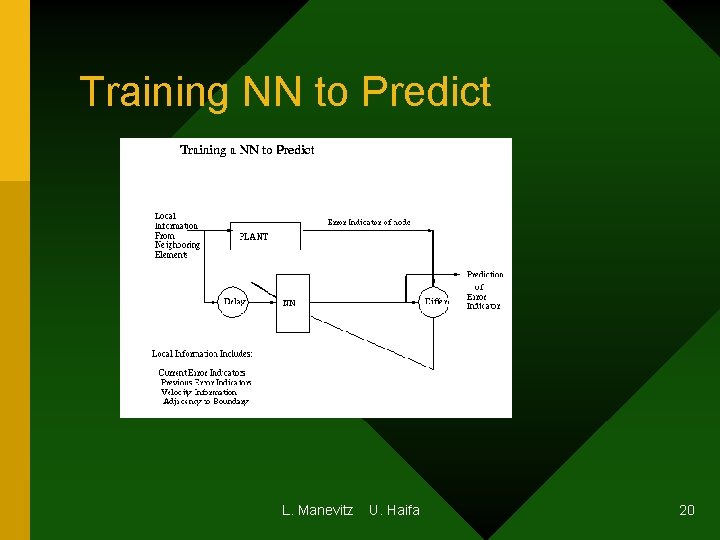
Training NN to Predict L. Manevitz U. Haifa 20

Finite Element Method • Numerical Method for solving p. d. e. s • Many user chosen parameters • Replace user expertise with NNs. L. Manevitz U. Haifa 21

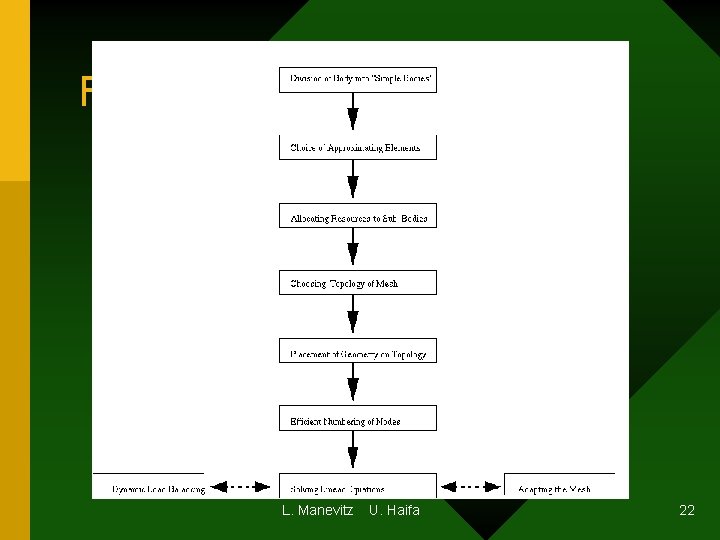
FEM Flow chart L. Manevitz U. Haifa 22

Problems and Methods L. Manevitz U. Haifa 23

Finite Element Method and Neural Networks • Place mesh on body • Predict where to adapt mesh L. Manevitz U. Haifa 24

Placing Mesh on Body (Manevitz, Givoli and Yousef) • Need to place geometry on topology • Method: Use Kohonen algorithm • Idea: Identify neurons with FEM nodes – Identify weights of nodes with geometric location – Identify topology with adjaceny – RESULT: Equi-probably placement L. Manevitz U. Haifa 25

Kohonen Placement for FEM • Include slide from Malik’s work. L. Manevitz U. Haifa 26

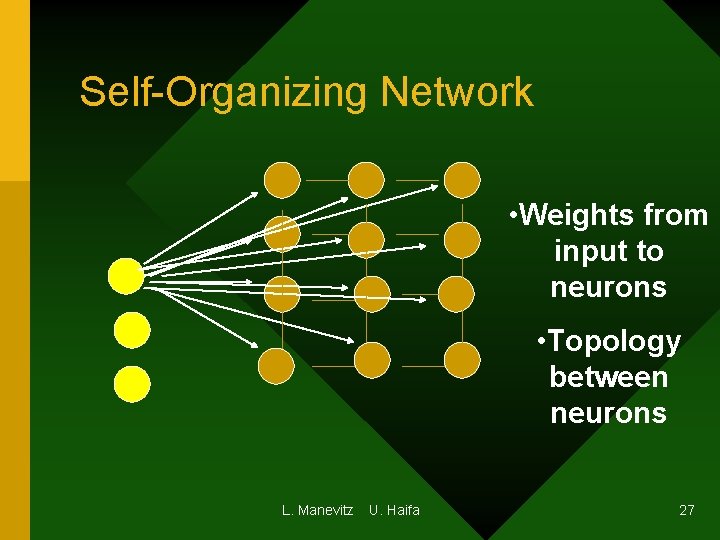
Self-Organizing Network • Weights from input to neurons • Topology between neurons L. Manevitz U. Haifa 27

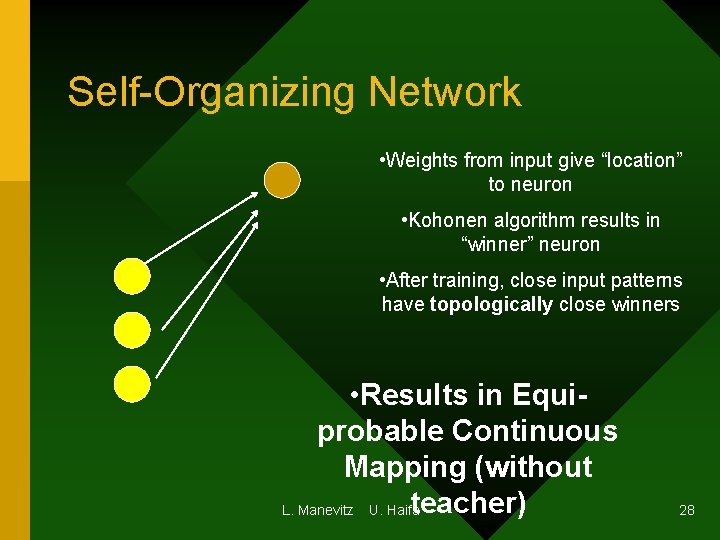
Self-Organizing Network • Weights from input give “location” to neuron • Kohonen algorithm results in “winner” neuron • After training, close input patterns have topologically close winners • Results in Equiprobable Continuous Mapping (without teacher) L. Manevitz U. Haifa 28

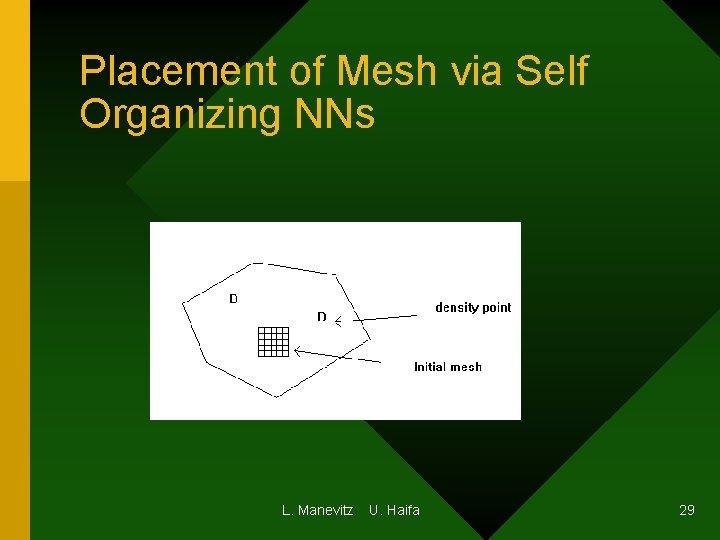
Placement of Mesh via Self Organizing NNs L. Manevitz U. Haifa 29

Placement of Mesh via Self Organizing NNs 2 Iteration 0 Iteration 6000; Quality =223 Iteration 500; Quality =288 Iteration 12000; Quality = 208 L. Manevitz U. Haifa Iteration 2000; Quality = 238 Iteration 30000; Quality =20230

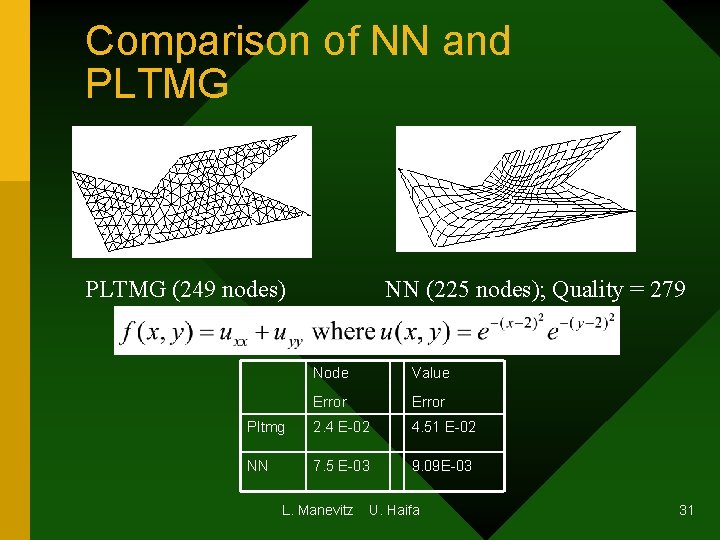
Comparison of NN and PLTMG (249 nodes) NN (225 nodes); Quality = 279 Node Value Error Pltmg 2. 4 E-02 4. 51 E-02 NN 7. 5 E-03 9. 09 E-03 L. Manevitz U. Haifa 31

FEM Temporal Adaptive Meshes L. Manevitz U. Haifa 32

Prediction of Refinement of Elements • Method simulates time • Current adaptive method uses gradient • Can just MISS all the action. • We use NNs to PREDICT the gradient. • Under development with Manevitz, Givoli and Bitar. L. Manevitz U. Haifa 33

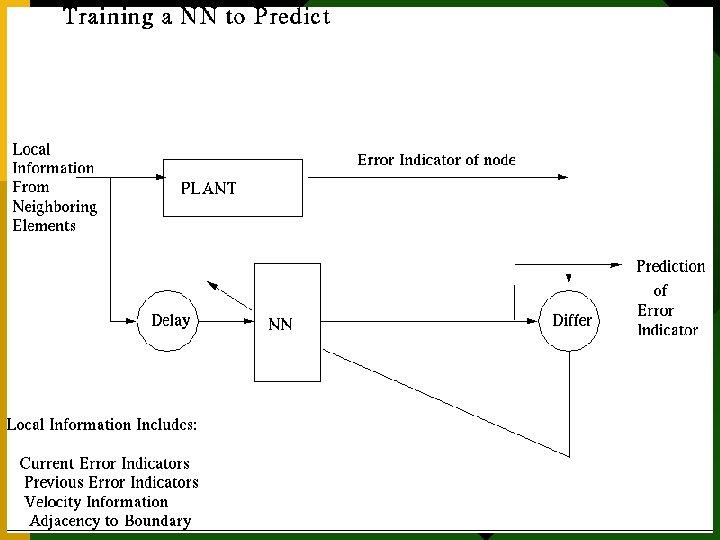
Training NN to Predict 2 L. Manevitz U. Haifa 34

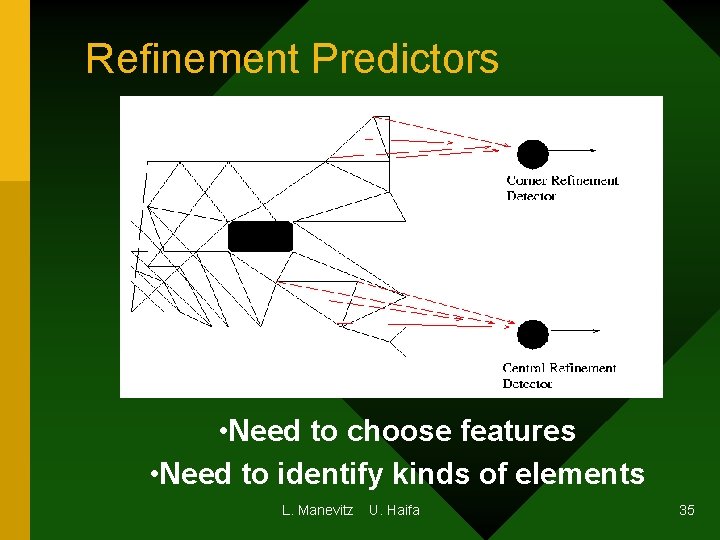
Refinement Predictors • Need to choose features • Need to identify kinds of elements L. Manevitz U. Haifa 35

Other Predictions? • Stock Market (really!) • Credit Card Fraud (Master Card, USA) L. Manevitz U. Haifa 36

Surfer’s Apprentice Program • Manevitz and Yousef • Make a “model” of user for retrieving information from internet. • Many issues: here focus on retrieval of new pages similar to other pages of interest to user. Note ONLY POSITIVE DATA. L. Manevitz U. Haifa 37

L. Manevitz U. Haifa 38

Bottleneck Network • Train to Identity on Sample Data • Should be identity only on similar data • NOVELTY FILTER L. Manevitz U. Haifa 39

How well does it work? • Tested on Standard Reuter’s Data Base. • Used 25% for training • Withholding information on representation • The best method for retrieval using only positive training. (Better than SVM, etc. ) L. Manevitz U. Haifa 40

How to help Intel? (Make Billions? Reset NASDAQ) • Branch prediction? • (Note similarity to FEM refinement. ) • Perhaps can use to give predictor that is even user or application dependent. • (Note: Neural activity is, I am told, natural for VLSI design and there have been several such chips produced. ) L. Manevitz U. Haifa 41

Other Different Directions • Modify basic model to handle temporal adaptivity. (Occurs in real neurons according to latest biological information. ) • Apply to model human diseases, etc. L. Manevitz U. Haifa 42