Neural Networks Background Neural Networks can be Biological

Neural Networks

Background - Neural Networks can be : - Biological models - Artificial models - Desire to produce artificial systems capable of sophisticated computations similar to the human brain.

Biological analogy and some main ideas • The brain is composed of a mass of interconnected neurons – each neuron is connected to many other neurons • Neurons transmit signals to each other • Whether a signal is transmitted is an all-or-nothing event (the electrical potential in the cell body of the neuron is thresholded) • Whether a signal is sent, depends on the strength of the bond (synapse) between two neurons

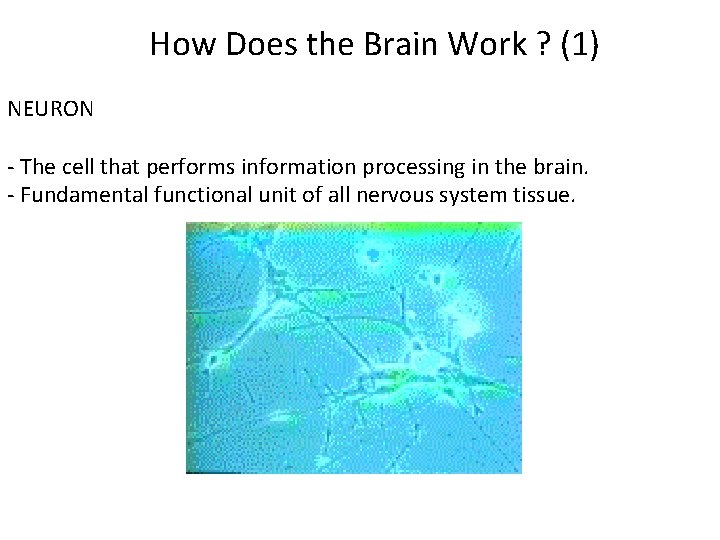
How Does the Brain Work ? (1) NEURON - The cell that performs information processing in the brain. - Fundamental functional unit of all nervous system tissue.

How Does the Brain Work ? (2) Each consists of : SOMA, DENDRITES, AXON, and SYNAPSE.

Brain vs. Digital Computers (1) - Computers require hundreds of cycles to simulate a firing of a neuron. - The brain can fire all the neurons in a single step. Parallelism - Serial computers require billions of cycles to perform some tasks but the brain takes less than a second. e. g. Face Recognition

Definition of Neural Network A Neural Network is a system composed of many simple processing elements operating in parallel which can acquire, store, and utilize experiential knowledge.

Artificial Neural Network? Neurons vs. Units (1) • Each element of NN is a node called unit. • Units are connected by links. • Each link has a numeric weight.

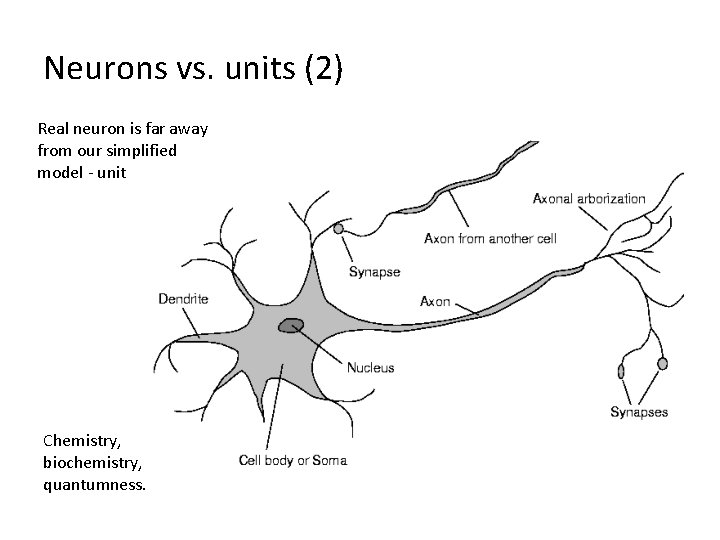
Neurons vs. units (2) Real neuron is far away from our simplified model - unit Chemistry, biochemistry, quantumness.

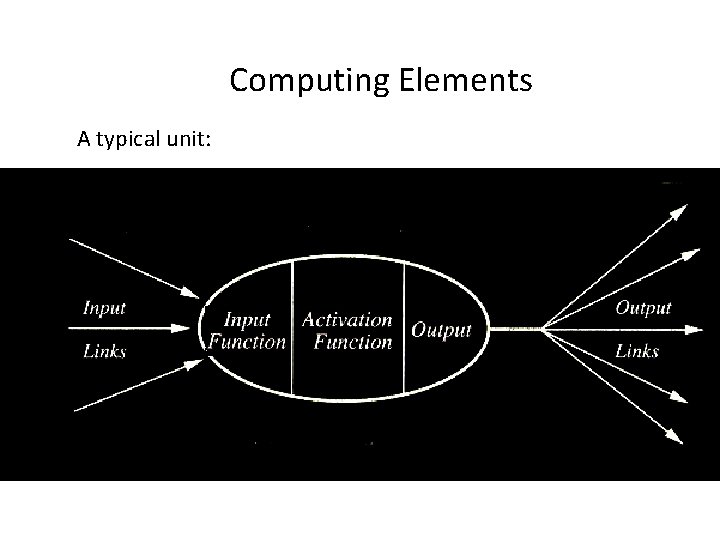
Computing Elements A typical unit:

Planning in building a Neural Network Decisions must be taken on the following: - The number of units to use. - The type of units required. - Connection between the units.

How NN learns a task. Issues to be discussed - Initializing the weights. - Use of a learning algorithm. - Set of training examples. - Encode the examples as inputs. - Convert output into meaningful results.

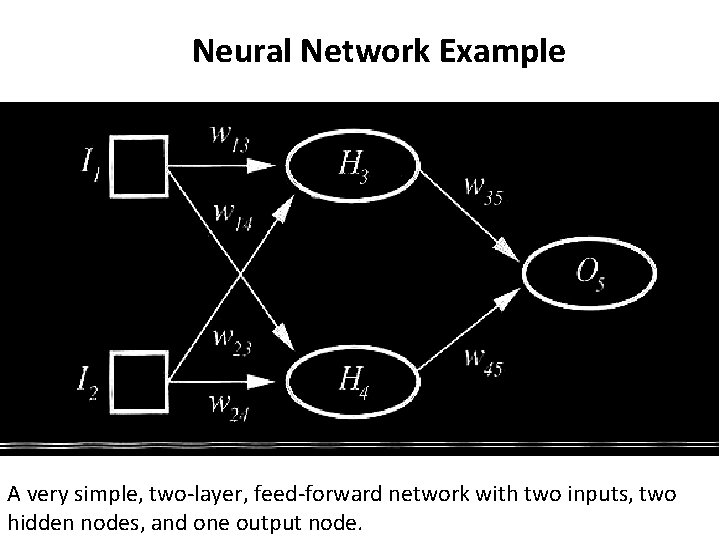
Neural Network Example A very simple, two-layer, feed-forward network with two inputs, two hidden nodes, and one output node.

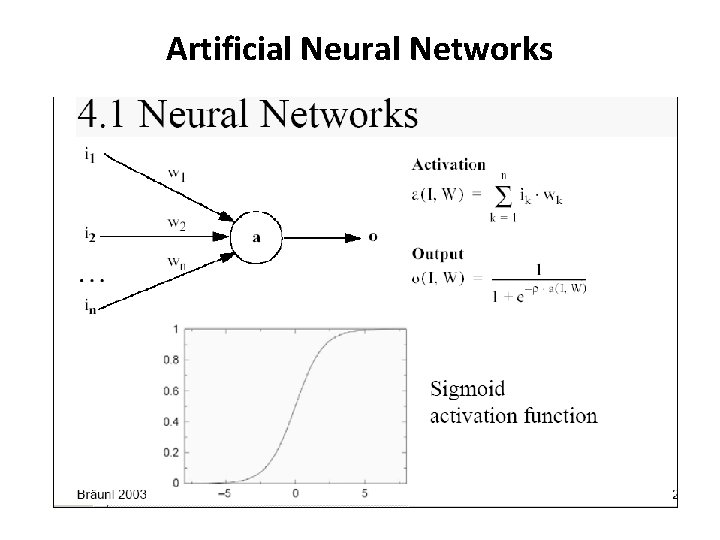
Simple Computations in this network - There are 2 types of components: Linear and Nonlinear. - Linear: Input function - calculate weighted sum of all inputs. - Non-linear: Activation function - transform sum into activation level.

Calculations Input function: Activation function g:

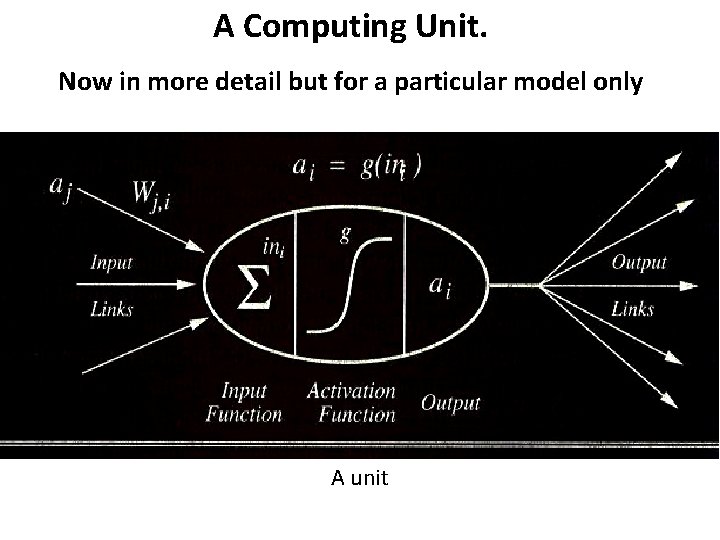
A Computing Unit. Now in more detail but for a particular model only A unit

Activation Functions - Use different functions to obtain different models. - 3 most common choices : 1) Step function 2) Sign function 3) Sigmoid function - An output of 1 represents firing of a neuron down the axon.

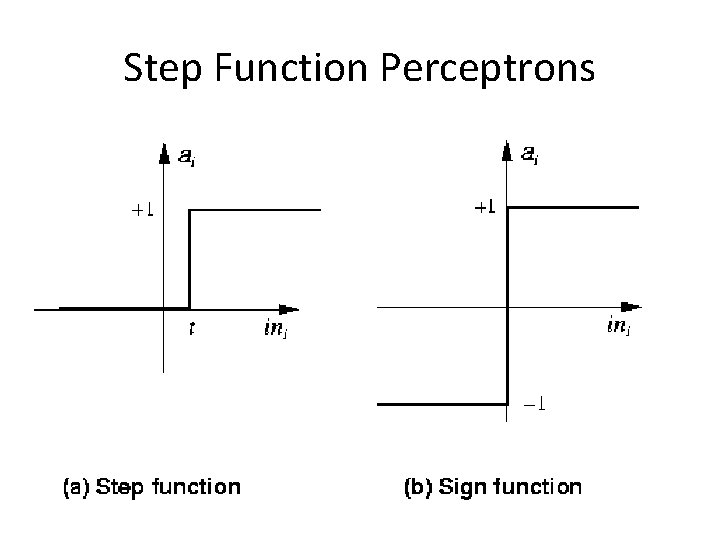
Step Function Perceptrons

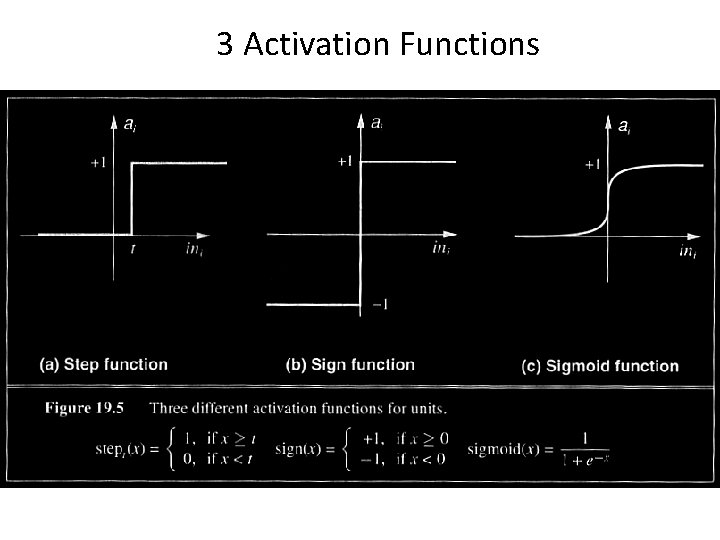
3 Activation Functions

Standard structure of an artificial neural network • Input units – represents the input as a fixed-length vector of numbers (user defined) • Hidden units – calculate thresholded weighted sums of the inputs – represent intermediate calculations that the network learns • Output units – represent the output as a fixed length vector of numbers

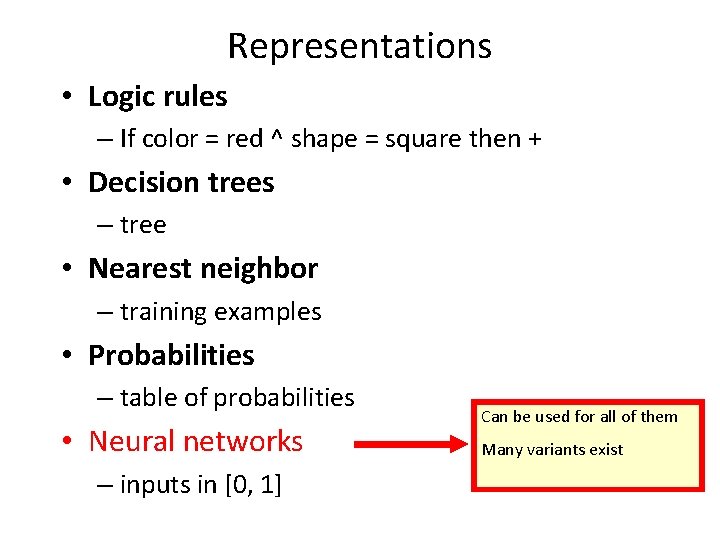
Representations • Logic rules – If color = red ^ shape = square then + • Decision trees – tree • Nearest neighbor – training examples • Probabilities – table of probabilities • Neural networks – inputs in [0, 1] Can be used for all of them Many variants exist

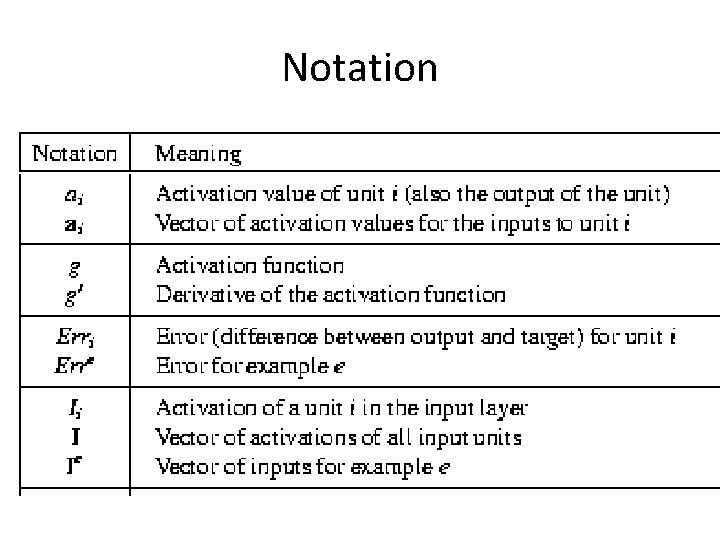
Notation

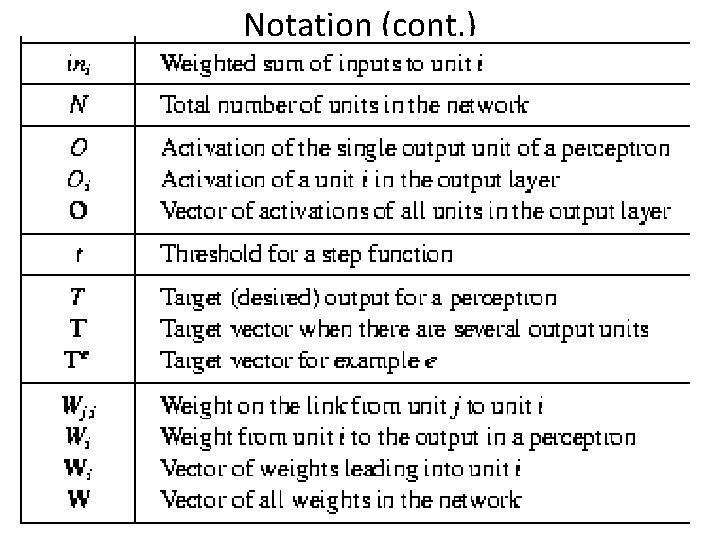
Notation (cont. )

Operation of individual units • Outputi = f(Wi, j * Inputj + Wi, k * Inputk + Wi, l * Inputl) – where f(x) is a threshold (activation) function – f(x) = 1 / (1 + e-Output) • “sigmoid” – f(x) = step function

Artificial Neural Networks

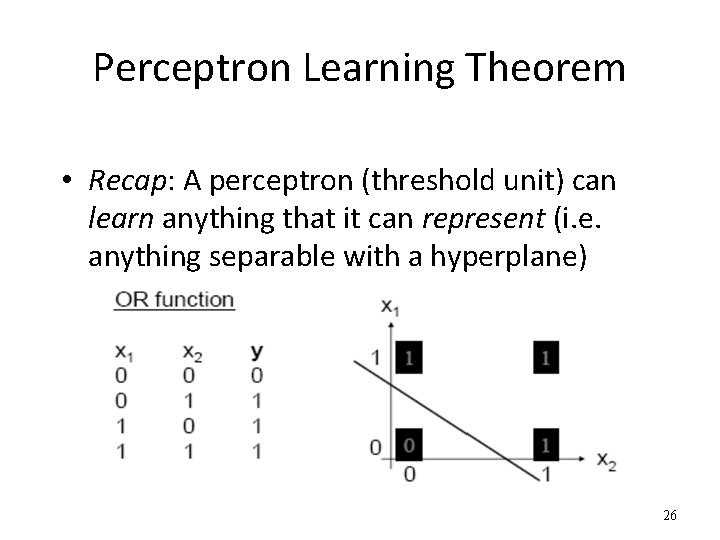
Perceptron Learning Theorem • Recap: A perceptron (threshold unit) can learn anything that it can represent (i. e. anything separable with a hyperplane) 26

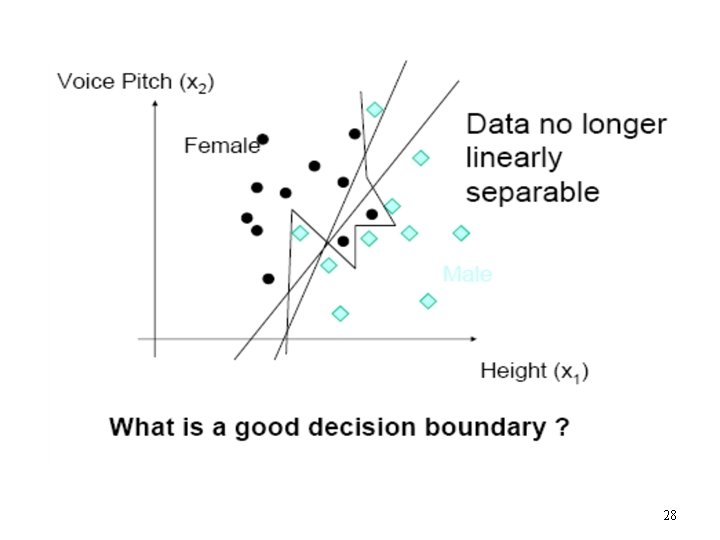
The Exclusive OR problem A Perceptron cannot represent Exclusive OR since it is not linearly separable. 27

28

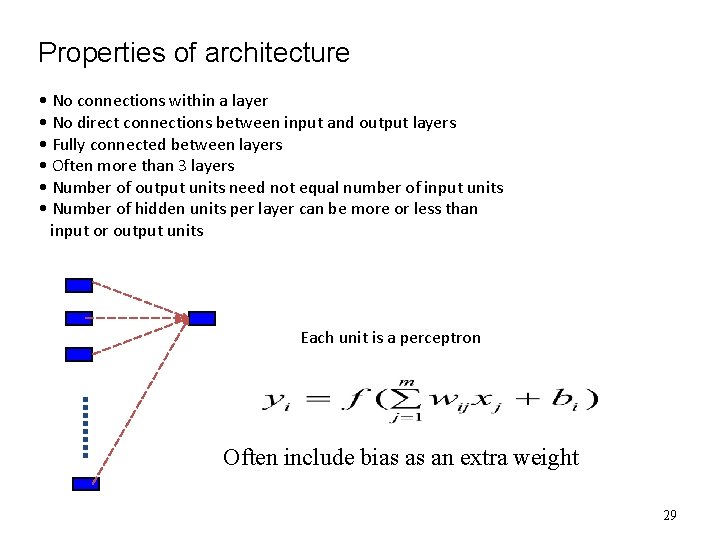
Properties of architecture • No connections within a layer • No direct connections between input and output layers • Fully connected between layers • Often more than 3 layers • Number of output units need not equal number of input units • Number of hidden units per layer can be more or less than input or output units Each unit is a perceptron Often include bias as an extra weight 29

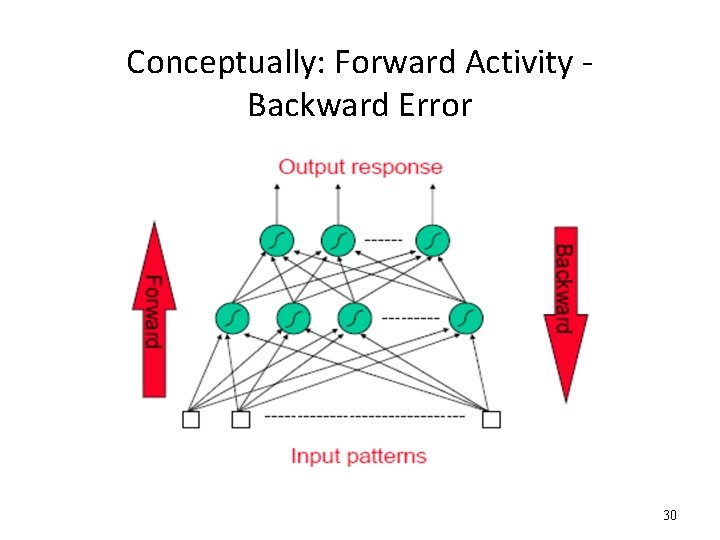
Conceptually: Forward Activity Backward Error 30

Backpropagation learning algorithm ‘BP’ Solution to credit assignment problem in MLP. Rumelhart, Hinton and Williams (1986) (though actually invented earlier in a Ph. D thesis relating to economics) BP has two phases: Forward pass phase: computes ‘functional signal’, feed forward propagation of input pattern signals through network Backward pass phase: computes ‘error signal’, propagates the error backwards through network starting at output units (where the error is the difference between actual and desired output values) 31

Forward Propagation of Activity • Step 1: Initialize weights at random, choose a learning rate η • Until network is trained: • For each training example i. e. input pattern and target output(s): • Step 2: Do forward pass through net (with fixed weights) to produce output(s) – i. e. , in Forward Direction, layer by layer: • • • Inputs applied Multiplied by weights Summed ‘Squashed’ by sigmoid activation function Output passed to each neuron in next layer – Repeat above until network output(s) produced 32

Step 3. Back-propagation of error 33

‘Back-prop’ algorithm summary (with Maths!) 34

‘Back-prop’ algorithm summary (with NO Maths!) 35

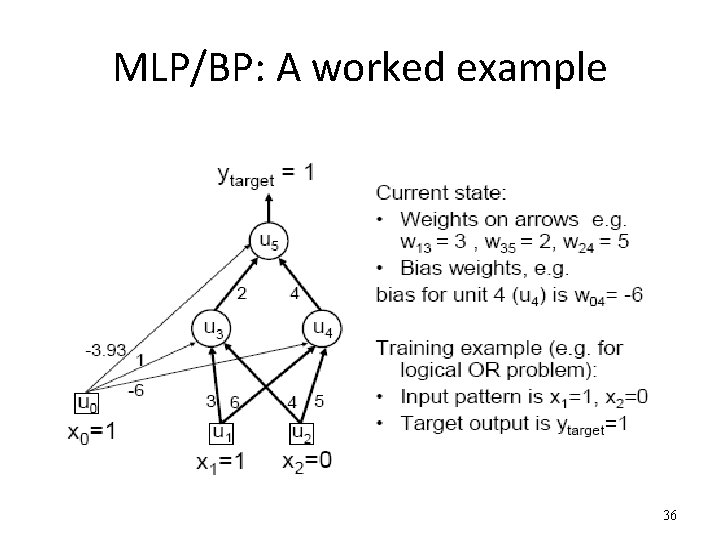
MLP/BP: A worked example 36

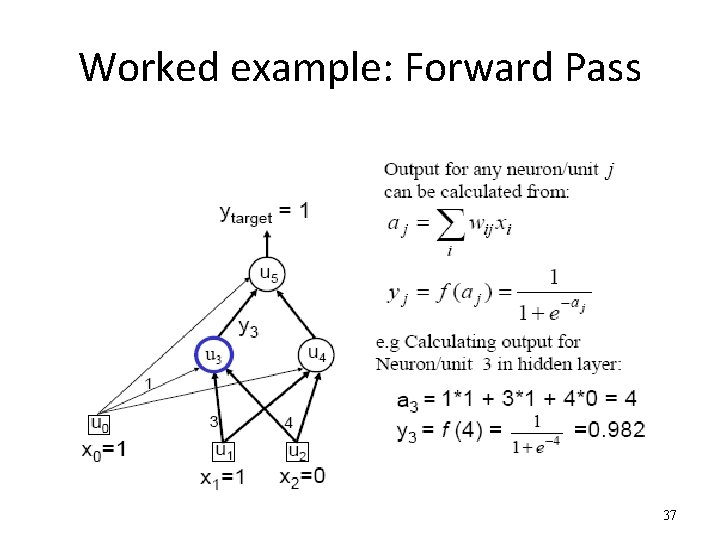
Worked example: Forward Pass 37

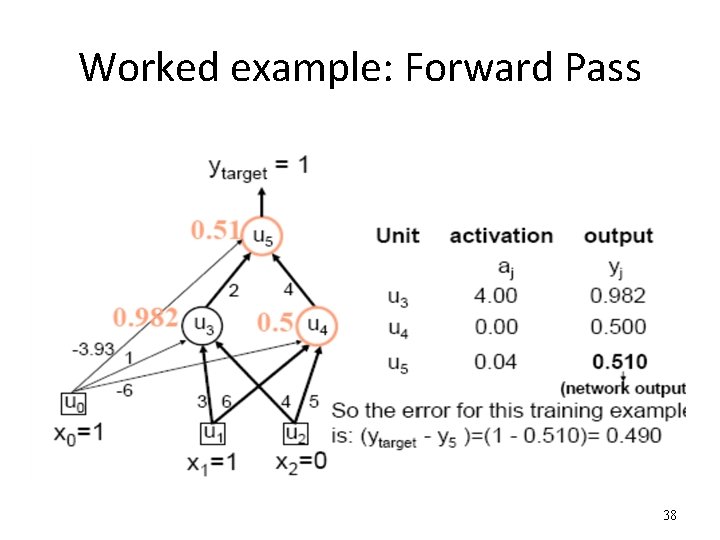
Worked example: Forward Pass 38

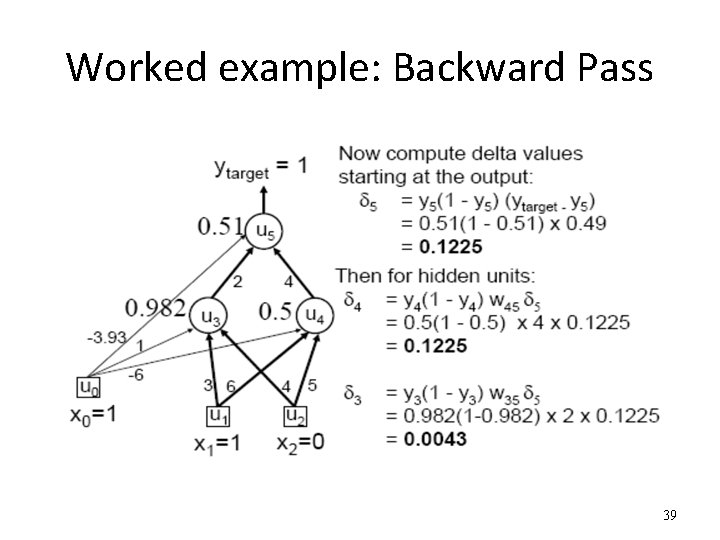
Worked example: Backward Pass 39

Worked example: Update Weights Using Generalized Delta Rule (BP) 40

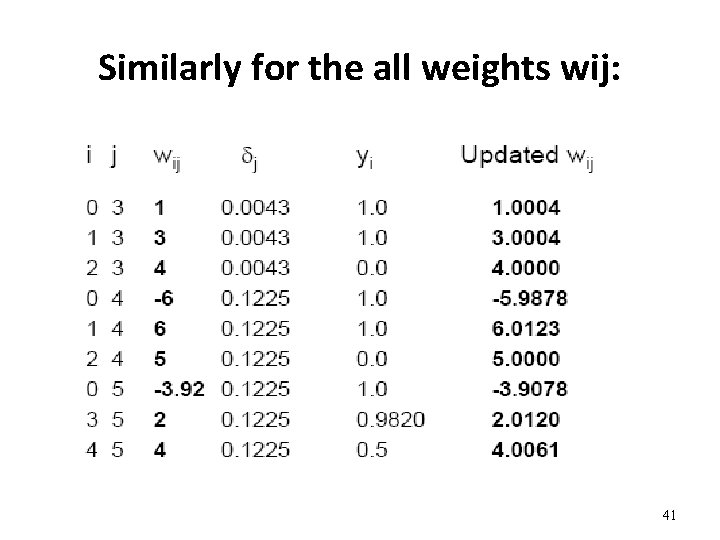
Similarly for the all weights wij: 41

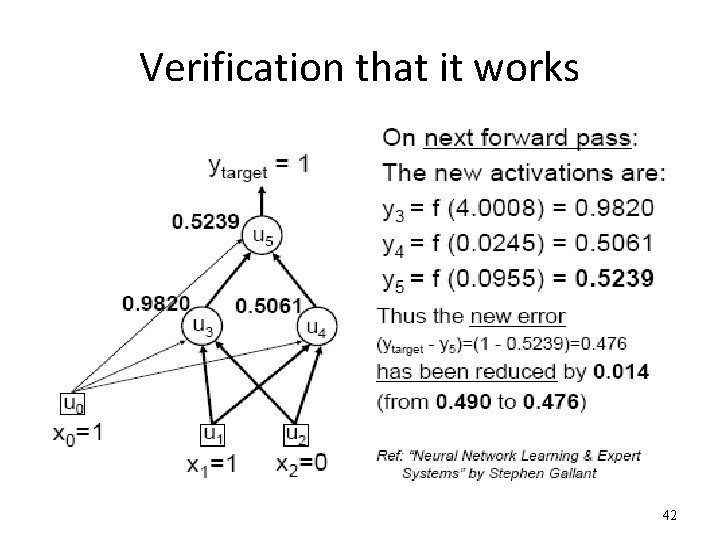
Verification that it works 42

Training • This was a single iteration of back-prop • Training requires many iterations with many training examples or epochs (one epoch is entire presentation of complete training set) • It can be slow ! • Note that computation in MLP is local (with respect to each neuron) • Parallel computation implementation is also possible 43

Training and testing data • How many examples ? – The more the merrier ! • Disjoint training and testing data sets – learn from training data but evaluate performance (generalization ability) on unseen test data • Aim: minimize error on test data 44

More resources • Binary Logic Unit in an example – http: //www. cs. usyd. edu. au/~irena/ai 01/nn/5. html • Multi. Layer Perceptron Learning Algorithm – http: //www. cs. usyd. edu. au/~irena/ai 01/nn/8. html 45