Neural Network Verification Part 2 Formulation SelfDriving Cars

Neural Network Verification Part 2: Formulation

Self-Driving Cars Human drivers replaced by deep neural networks

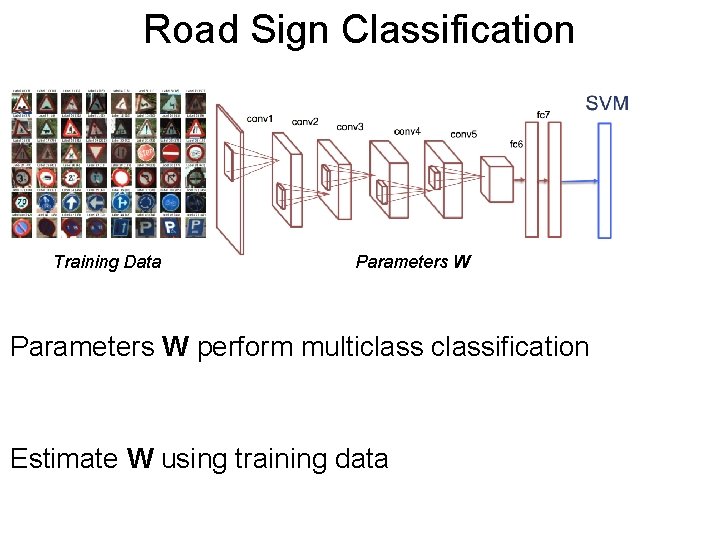
Road Sign. Post Classification Training Data Parameters W perform multiclassification Estimate W using training data

Road Sign. Post Classification Test Image Parameters W select the class of a new input image

Road Sign. Post Classification Test Image Parameters W Small deformations can cause fatal errors Input Image Prediction Blurring, Saturation Aung et al. , 2017 Input Image Prediction Pixel Errors Evtimov et al. , 2017

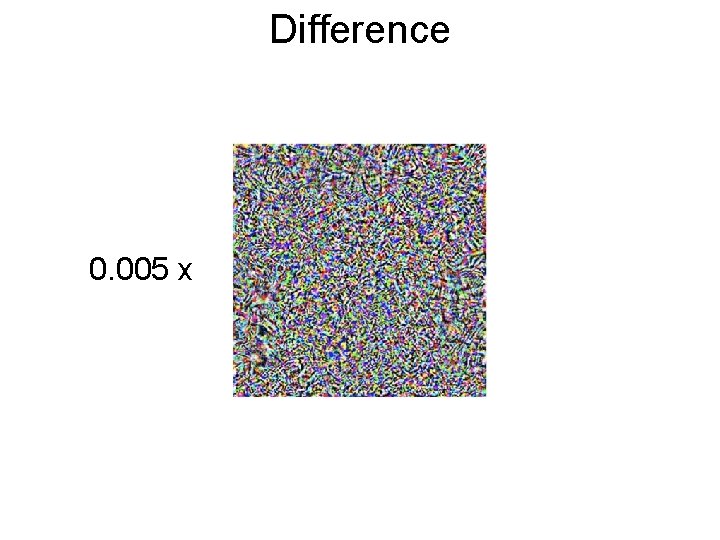
Spot the Difference “pig” (91%) “airliner” (99%)

Difference 0. 005 x

Glasses Sharif, Bhagavatula, Bauer and Reiter, 2016

3 D Object Athalye, Engstrom, Ilyas and Kwok, 2017

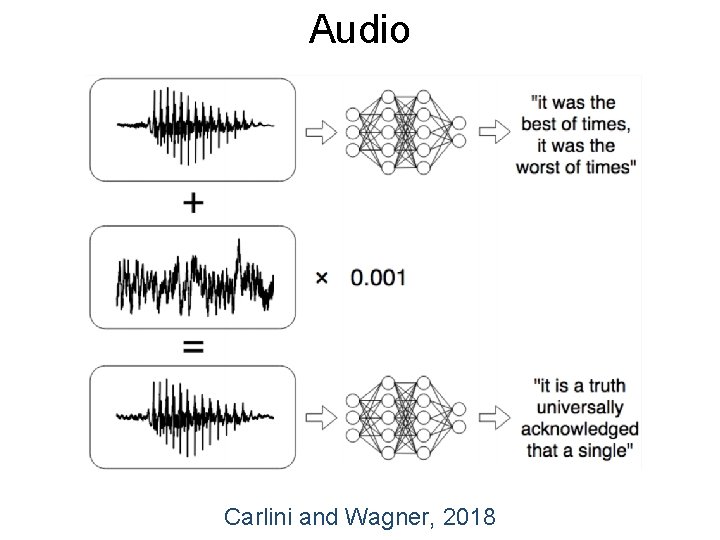
Audio Carlini and Wagner, 2018

Outline • Robust Deep Learning • Formulation • Black Box Solvers

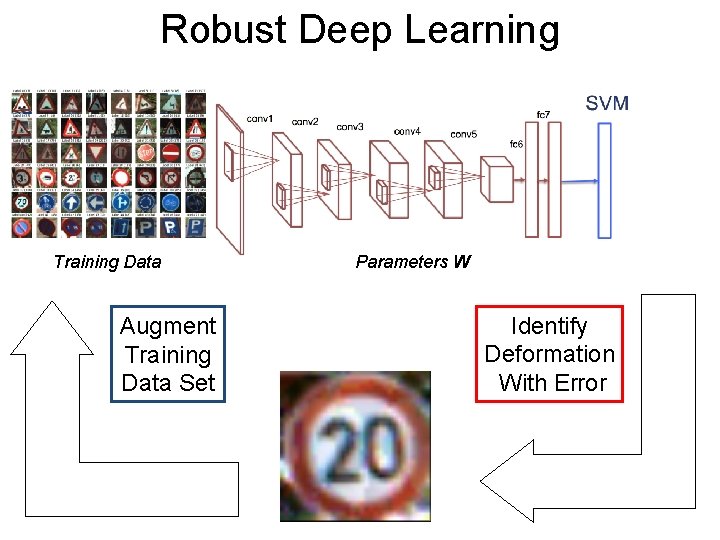
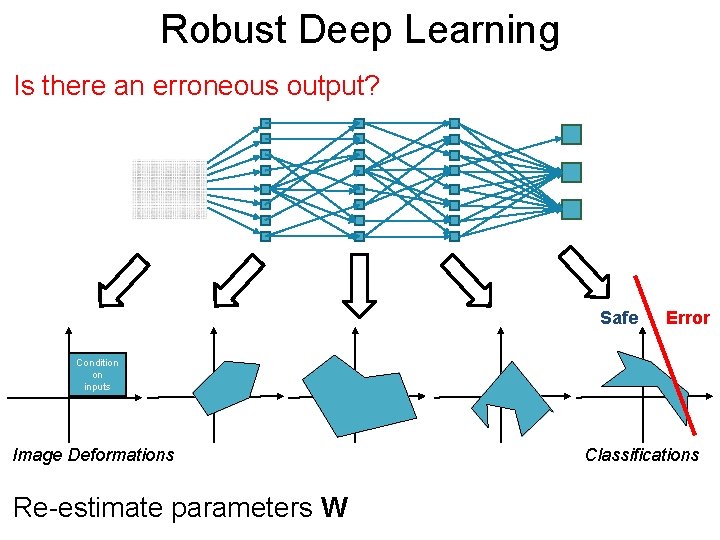
Robust Deep Post. Learning Training Data Augment Training Data Set Parameters W Identify Deformation With Error

Robust Deep Post. Learning Is there an erroneous output? Safe Error Condition on inputs Image Deformations Re-estimate parameters W Classifications

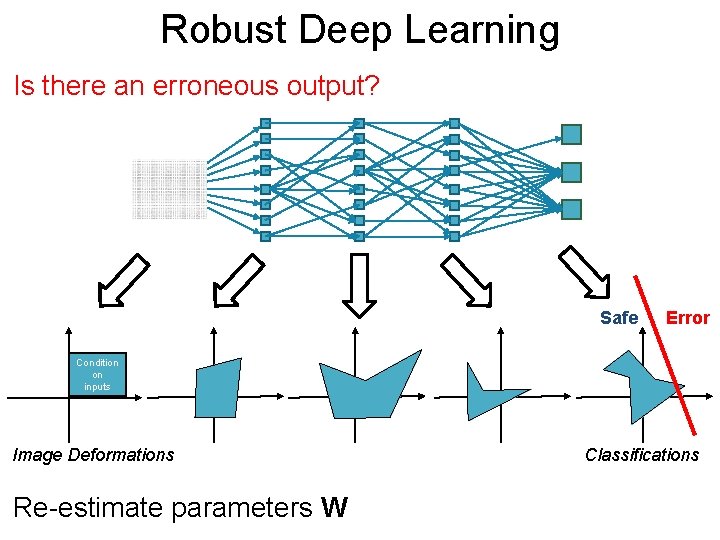
Robust Deep Post. Learning Is there an erroneous output? Safe Error Condition on inputs Image Deformations Re-estimate parameters W Classifications

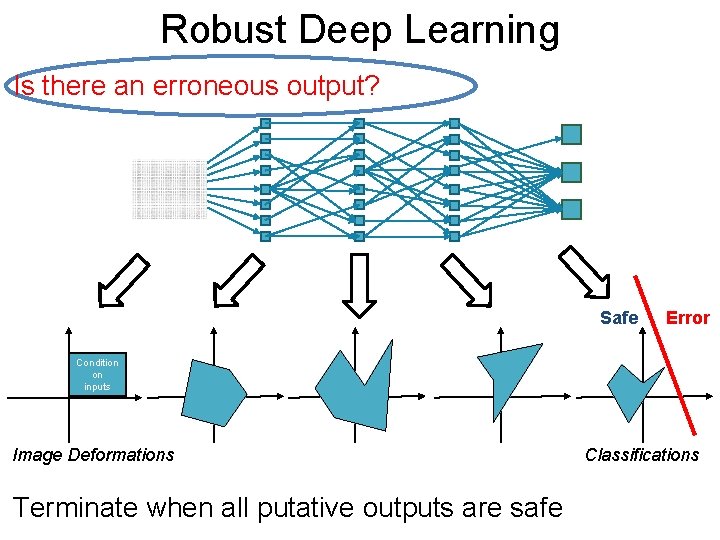
Robust Deep Post. Learning Is there an erroneous output? Safe Error Condition on inputs Image Deformations Terminate when all putative outputs are safe Classifications

Erroneous Post. Output Set of possible inputs x ∈ X E. g. X is an l∞ ball around an input x* Ground-truth class is y* Score for input x and class y is s(y; x)

Erroneous Post. Output Find x ∈ X such that miny≠y* (s(y*; x) – s(y; x)) < 0 I. e. an input that is misclassified Or prove that there does not exist such an x An instance of Neural Network Verification

Outline • Robust Deep Learning • Formulation • Black Box Solvers

Assumption Post Piecewise linear non-linearities Re. LU, Max. Pool … Covers many state of the art networks Intuitions can be transferred to more general settings

Neural Network Post. Verification Neural network f Scalar output z = f(x) E. g. in binary classification, z = s(y*; x) – s(y; x) for y ≠ y* Property: f(x) > 0 for all x ∈ X Formally prove the property, or provide counter-example

Complex Properties Post OR clause e. g. (z 1 > 0) ∨ (z 2 > 0) ∨ (z 3 > 0) max(z 1, z 2, z 3) > 0 Implement using a Max. Pool layer at the end

Complex Properties Post AND clause e. g. (z 1 > 0) ∧ (z 2 > 0) ∧ (z 3 > 0) min(z 1, z 2, z 3) > 0 -max(-z 1, -z 2, -z 3) > 0 Linear + Max. Pool + Linear layer at the end

Complex Properties Post Boolean formulas OR over linear inequalities AND over linear inequalities Any Boolean formula over linear inequalities

Example Post min s. t. a 1 [-2, 2] x 1 z [-2, 2] 1 x 2 -1 -1 b Prove that z > -5 -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 -1 1 z ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout

Example Post min Linear constraints Easy to handle s. t. z -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout

Example Post min s. t. z -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 Non-linear constraints aout = max{ain, 0} bout = max{bin, 0} NP-hard problem z = - aout - bout

Outline • Robust Deep Learning • Formulation • Black Box Solvers Cheng et al. , 2017; Lomuscio et al. , 2017; Tjeng et al. , 2017

Reformulation Post aout = max{ain, 0} Large constant Ma (greater than any possible ain) Binary variable δa ∈ {0, 1} aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma

Reformulation Post aout = max{ain, 0} Large constant Ma (greater than any possible ain) Binary variable δa ∈ {0, 1} aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma Case I: δa = 0

Reformulation Post aout = max{ain, 0} Large constant Ma (greater than any possible ain) Binary variable δa ∈ {0, 1} aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma Case I: δa = 0 aout = 0

Reformulation Post aout = max{ain, 0} Large constant Ma (greater than any possible ain) Binary variable δa ∈ {0, 1} aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma Case II: δa = 1

Reformulation Post aout = max{ain, 0} Large constant Ma (greater than any possible ain) Binary variable δa ∈ {0, 1} aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma Case II: δa = 1 aout = ain

Example Post min s. t. z -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout = max{ain, 0} bout = max{bin, 0} z = - aout - bout

Example Post min s. t. z -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma bout = max{bin, 0} δa ∈ {0, 1} z = - aout - bout

Example Post min Mixed Integer Linear Program s. t. z -2 ≤ x 1 ≤ 2 -2 ≤ x 2 ≤ 2 ain = x 1 + x 2 bin = x 1 - x 2 aout ≥ ain aout ≥ 0 aout ≤ ain + (1 -δa)Ma aout ≤ δa. Ma bout ≥ bin bout ≥ 0 bout ≤ bin + (1 -δb)Mb bout ≤ δb. Mb δa ∈ {0, 1} δb ∈ {0, 1} z = - aout - bout

MILP Formulation Post Neural network structure can help determine Ma Standard solvers e. g. Gurobi, Mosek, CPLEX Does not scale (we will see results later) Standard architectures have order of 107 parameters

Questions?