NEURAL NETWORK THEORY NEURONAL DYNAMICS ACTIVATIONS AND SIGNALS

NEURAL NETWORK THEORY NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS 欢迎大家提出意见建议！ 2003. 10. 15

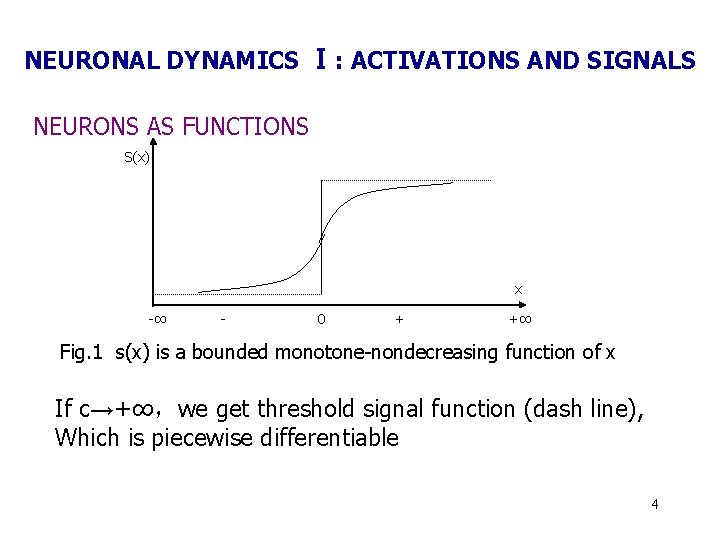
NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS Neurons behave as functions. Neurons transduce an unbounded input activation x(t) at time t into a bounded output signal S(x(t)). 2

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS The transduction description: a sigmoidal or S-shaped curve the logistic signal function: The logistic signal function is sigmoidal and strictly increases for positive scaling constant c >0. 3

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONS AS FUNCTIONS S(x) x -∞ - 0 + +∞ Fig. 1 s(x) is a bounded monotone-nondecreasing function of x If c→+∞，we get threshold signal function (dash line), Which is piecewise differentiable 4

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY In general, signal functions are monotone nondecreasing S’>=0. This means signal functions have an upper bound or saturation value. The staircase signal function is a piecewise-differentiable Monotone-nondecreasing signal function. 5

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY An important exception: bell-shaped signal function or Gaussian signal functions The sign of the signal-activation derivation s’ is opposite the sign of the activation x. We shall assume signal functions are monotone nondecreasing unless stated otherwise. 6

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY Generalized Gaussian signal function define potential or radial basis function : input activation vector: variance: mean vector: we shall consider only scalar-input signal functions: 7

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY neurons are nonlinear but not too much so ---- a property as semilinearity Linear signal functions - make computation and analysis comparatively easy - do not suppress noise - linear network are not robust Nonlinear signal functions - increases a network’s computational richness increases a network’s facilitates noise suppression risks computational and analytical intractability favors dynamical instability 8

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL MONOTONICITY Signal and activation velocities the signal velocity: =d. S/dt Signal velocities depend explicitly on action velocities 9

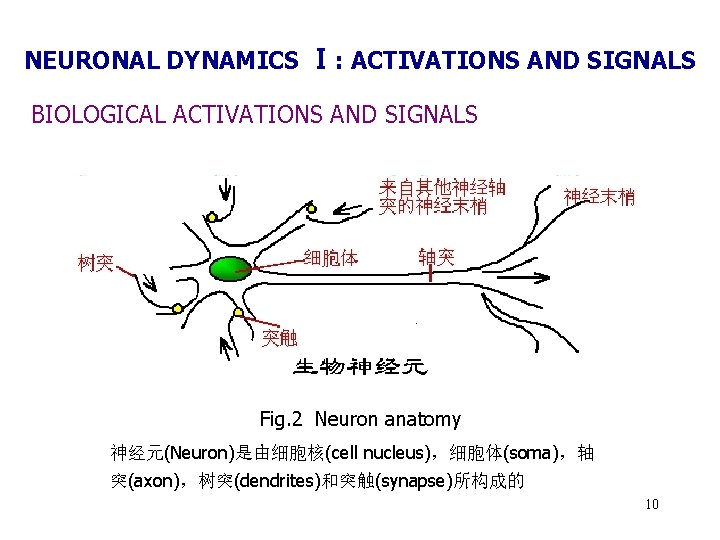
NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS BIOLOGICAL ACTIVATIONS AND SIGNALS Fig. 2 Neuron anatomy 神经元(Neuron)是由细胞核(cell nucleus)，细胞体(soma)，轴 突(axon)，树突(dendrites)和突触(synapse)所构成的 10

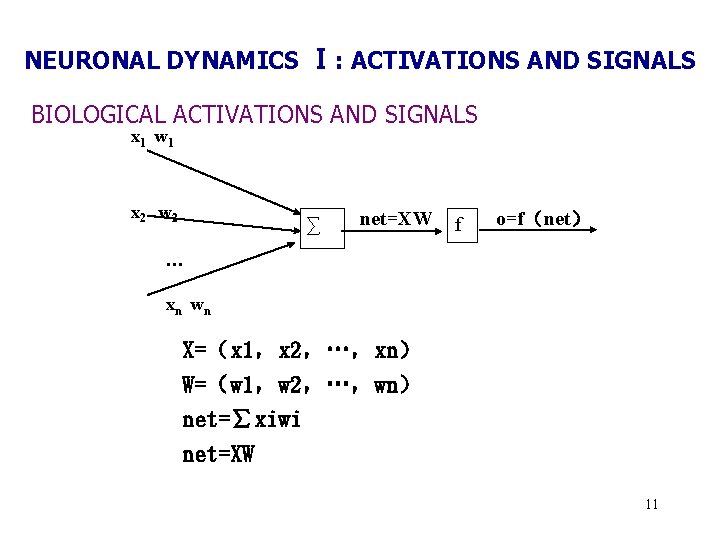
NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS BIOLOGICAL ACTIVATIONS AND SIGNALS x 1 w 1 x 2 w 2 ∑ net=XW f o=f（net） … xn wn X=（x 1，x 2，…，xn） W=（w 1，w 2，…，wn） net=∑xiwi net=XW 11

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS BIOLOGICAL ACTIVATIONS AND SIGNALS Competitive Neuronal Signal The neuron “wins” at time t if , “loses” if and otherwise possesses a fuzzy win-loss status between 0 an 1. a. Binary signal functions : [0, 1] b. Bipolar signal functions : [-1, 1] Mc. Culloch—Pitts (M—P) neurons logical signal function ( Binary Bipolar ) 12

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURON FIELDS Neurons within a field are topologically ordered, often by proximity. zeroth-order topology : lack of topological structure Denotation: , neural system samples the function associated pairs , . . . , , m times to generate the The overall neural network behaves as an adaptive filter and sample data changed network parameters. 13

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONAL DYNAMICAL SYSTEMS Description: a system of first-order differential or difference equations that govern the time evolution of the neuronal activations or membrane potentials Activation differential equations: (1) (2) in vector notation: (3) (4) 14

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONAL DYNAMICAL SYSTEMS Neuronal State spaces So the state space of the entire neuronal dynamical system is: Augmentation : 15

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONAL DYNAMICAL SYSTEMS Signal state spaces as hyper-cubes The signal state of field at time t: The signal state space: an n-dimensional hypercube The unit hypercube : or , The relationship between hyper-cubes and the fuzzy set : , subsets of correspond to the vertices of 16

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS NEURONAL DYNAMICAL SYSTEMS Neuronal activations as short-term memory Short-term memory(STM) : activation Long-term memory(LTM) : synapse 17

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 1、Liner Function S(x) = cx + k , c>0 S k o x 18

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 2. Ramp Function r if x≥θ S(x)= cx if |x|<θ -r if x≤-θ r>0, r is a constant. S r θ -θ x -r 19

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 3、threshold linear signal function: a special Ramp Function Another form: 20

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 4、logistic signal function: Where c>0. So the logistic signal function is monotone increasing. 21

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 5、threshold signal function: Where T is an arbitrary real-valued threshold, and k indicates the discrete time step. 22

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 6、hyperbolic-tangent signal function: Another form: 23

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 7、threshold exponential signal function: When , 24

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 8、exponential-distribution signal function: When , 25

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 9、the family of ratio-polynomial signal function: An example For , 26

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 27

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS SIGNAL FUNCTION (ACTIVATION FUNCTION) 28

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS PULSE-CODED SIGNAL FUNCTION Definition: (5) (6) where (7) 29

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS PULSE-CODED SIGNAL FUNCTION Pulse-coded signals take values in the unit interval [0, 1]. Proof: when 30

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS PULSE-CODED SIGNAL FUNCTION Velocity-difference property of pulse-coded signals The first-order linear inhomogenous differential equation: The solution to this differential equation: (8) (9) (5) A simple form for the signal velocity: (10) (11) 31

NEURONAL DYNAMICS Ⅰ: ACTIVATIONS AND SIGNALS PULSE-CODED SIGNAL FUNCTION (10) The central result of pulse-coded signal functions: The instantaneous signal-velocity equals the current pulse minus the current expected pulse frequency. ------- the velocity-difference property of pulsecoded signal functions 32