Neural Network Similarity Joel Lehman Outline Genetic Algorithms

Neural Network Similarity Joel Lehman

Outline Genetic Algorithms n Neural Networks n Evolving Neural Networks n Neural Network Similarity Problem n NP-Completeness Proof n

Genetic Algorithms Inspired by the apparent power of Natural Evolution n Usually applied to optimization problems n Consists of: n ¨A population of candidate solutions ¨ A mechanism for generating variation ¨ A measure of goodness used for selection

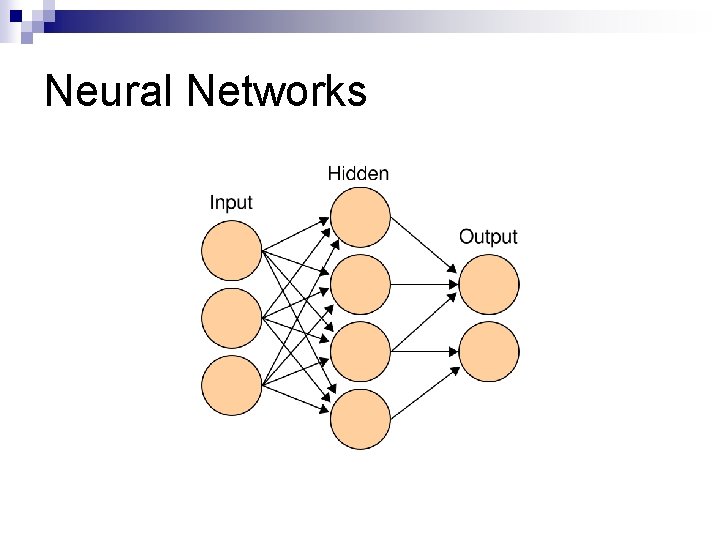
Neural Networks Computational abstraction of biological brains n Consist of nodes (neurons) and connections (synapses) n Can be drawn as a weighted digraph n

Neural Networks

Evolving Neural Networks n n n Intelligence on earth evolved in form of biological brains Using GA+NN is a very rough abstraction of how intelligence evolved Can be used in many tasks ¨ Robot n control, game playing, classification, etc. How to define genetic operators that operate on NN?

Evolving Neural Networks n Use a ‘direct encoding’ ¨ Represent n NN directly as a graph Mutation is easy ¨ Simply add new connections, nodes, or change connection weights n Crossover is hard ¨ How to recognize what parts of one NN correspond to parts of another ¨ Without this idea of ‘homology’ naïve crossover will likely just destroy the functionality of both NN

Neural Network Similarity Problem Basically, question is: what parts of one NN are relatively the same to parts of a second NN n If we know this, we can intelligently do crossover to create meaningful offspring NN n

Neural Network Similarity Problem n n n A Neural Network is composed of a 4 -tuple: (Input Nodes, Output Nodes, Hidden Nodes, Connections) Two NNs are ‘compatible’ if they share same Input and Output Nodes A subnetwork of a neural network A is a NN compatible with A, with hidden nodes and connections that are subsets of those in A

Neural Network Similarity Problem Given two compatible NNs, N 1 and N 2, an integer k, and a real number l n Does there exist a subnetwork NS 1 of N 1 with at least k connections isomorphic (disregarding connection weights) to a subnetwork NS 2 of N 2 such that the summed difference in connection weights between NS 1 and NS 2 are less than l. n

NP Completeness Proof First we must show it is in NP. n A witness can give the partial map between hidden nodes and connections in N 1 to N 2. It can then be verified in polynomial time that the conditions of k and l are satisfied n

NP Completeness Proof Basically this is an augmented version of subgraph isomorphism n Subgraph isomorphism n ¨ Given two graphs G 1, G 2, does there exist a subgraph of G 1 with at least k edges that is isomorphic to a subgraph of G 2?

NP Completeness Proof n Easy to map an instance of SGI into NNSP: ¨ Create a NN from each graph by the following: n Set input and output nodes to null set n Vertices in the graph translate directly to hidden nodes n Edges in the graph translate directly to connections in the NN all with identical weights ¨K in NNSP is set to k from SGI ¨ L in NNSP is set to 0 n Intuitively we know this works ¨ We’ve stripped away all the augmentations

NP Completeness Proof n Given yes instance of SGI ¨ The mapped instance of NNSP will also have an subgraph isomorphism, the NNs are isomorphic to the given graphs, and the L criterion is satisfied n Given yes instance of NNSP ¨ We know there are no hidden/input nodes ¨ All weights are 1. 0 (and thus insignificant to L criterion) ¨ The isomorphism between NN/Graph and the decision question means there must be a SGI of size k

Questions?