Neural Nets Using Backpropagation n n Chris Marriott

Neural Nets Using Backpropagation n n Chris Marriott Ryan Shirley CJ Baker Thomas Tannahill

Agenda n n n Review of Neural Nets and Backpropagation: The Math Advantages and Disadvantages of Gradient Descent and other algorithms Enhancements of Gradient Descent Other ways of minimizing error

Review n n n Approach that developed from an analysis of the human brain Nodes created as an analog to neurons Mainly used for classification problems (i. e. character recognition, voice recognition, medical applications, etc. )

Review n Neurons have weighted inputs, threshold values, activation function, and an output Weighted inputs Output Activation function = f( S(inputs * weight))

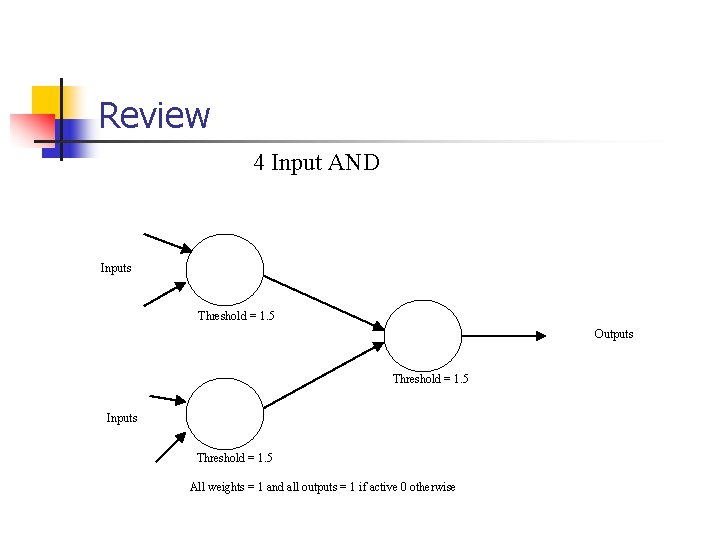
Review 4 Input AND Inputs Threshold = 1. 5 Outputs Threshold = 1. 5 Inputs Threshold = 1. 5 All weights = 1 and all outputs = 1 if active 0 otherwise

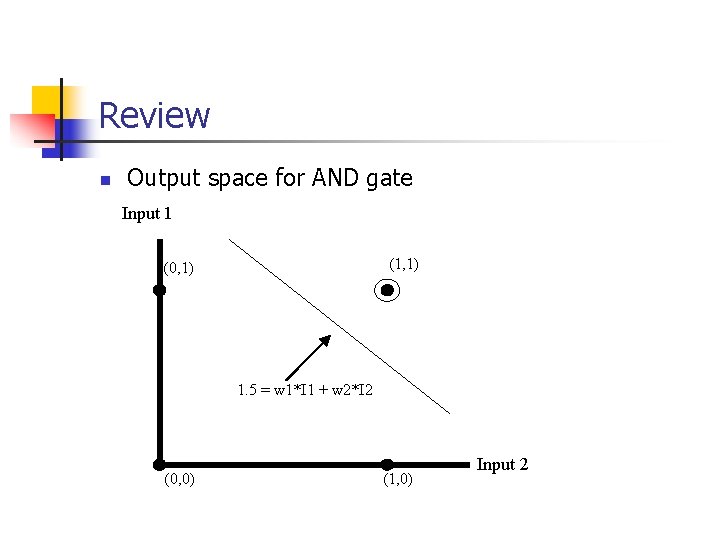
Review n Output space for AND gate Input 1 (1, 1) (0, 1) 1. 5 = w 1*I 1 + w 2*I 2 (0, 0) (1, 0) Input 2

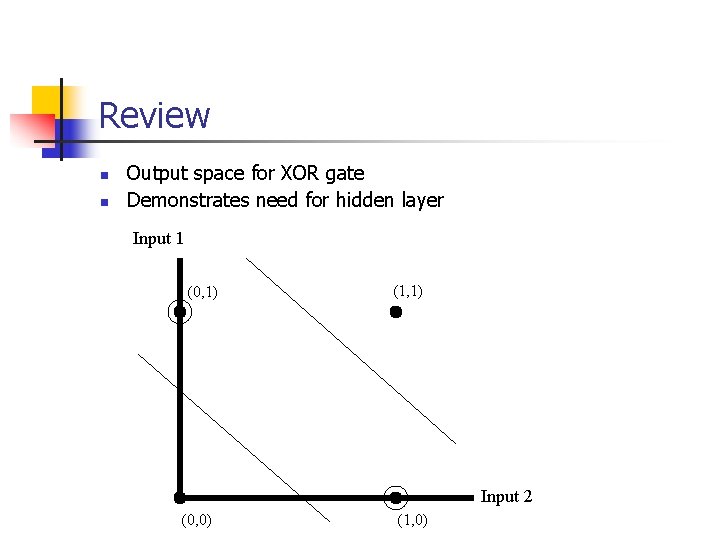
Review n n Output space for XOR gate Demonstrates need for hidden layer Input 1 (0, 1) (1, 1) Input 2 (0, 0) (1, 0)

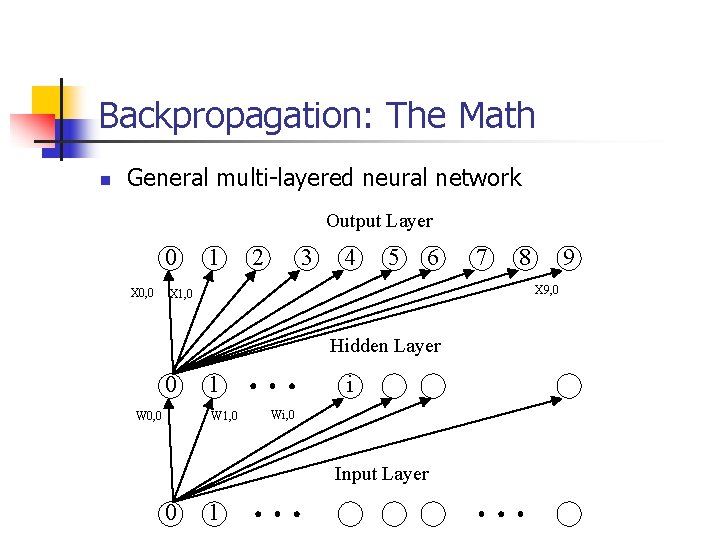
Backpropagation: The Math n General multi-layered neural network Output Layer 0 X 0, 0 1 2 3 4 5 6 Hidden Layer 1 W 1, 0 W 0, 0 i Wi, 0 Input Layer 0 8 9 X 9, 0 X 1, 0 0 7 1

Backpropagation: The Math n Backpropagation n Calculation of hidden layer activation values

Backpropagation: The Math n Backpropagation n Calculation of output layer activation values

Backpropagation: The Math n Backpropagation n Calculation of error dk = f(Dk) -f(Ok)

Backpropagation: The Math n Backpropagation n Gradient Descent objective function n Gradient Descent termination condition

Backpropagation: The Math n Backpropagation n Output layer weight recalculation Learning Rate (eg. 0. 25) Error at k

Backpropagation: The Math n Backpropagation n Hidden Layer weight recalculation

Backpropagation Using Gradient Descent n Advantages n n n Relatively simplementation Standard method and generally works well Disadvantages n n Slow and inefficient Can get stuck in local minima resulting in sub-optimal solutions

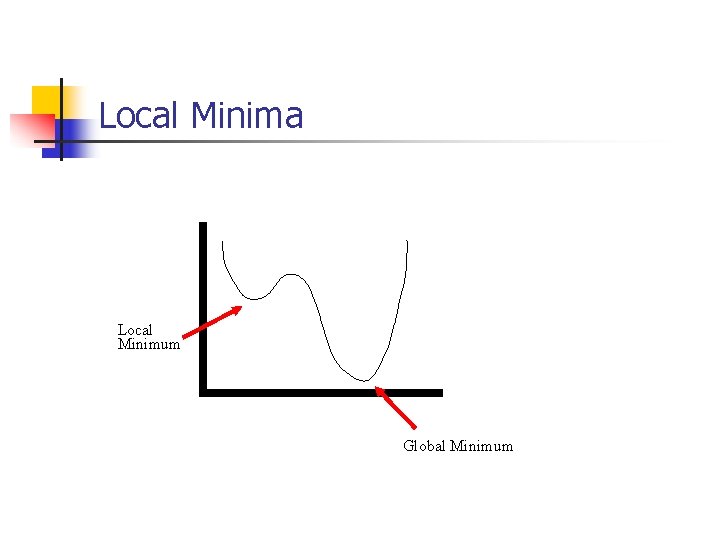
Local Minima Local Minimum Global Minimum

Alternatives To Gradient Descent n Simulated Annealing n n Advantages n Can guarantee optimal solution (global minimum) Disadvantages n n May be slower than gradient descent Much more complicated implementation

Alternatives To Gradient Descent n Genetic Algorithms/Evolutionary Strategies n Advantages n n n Faster than simulated annealing Less likely to get stuck in local minima Disadvantages n n Slower than gradient descent Memory intensive for large nets

Alternatives To Gradient Descent n Simplex Algorithm n Advantages n n n Similar to gradient descent but faster Easy to implement Disadvantages n Does not guarantee a global minimum

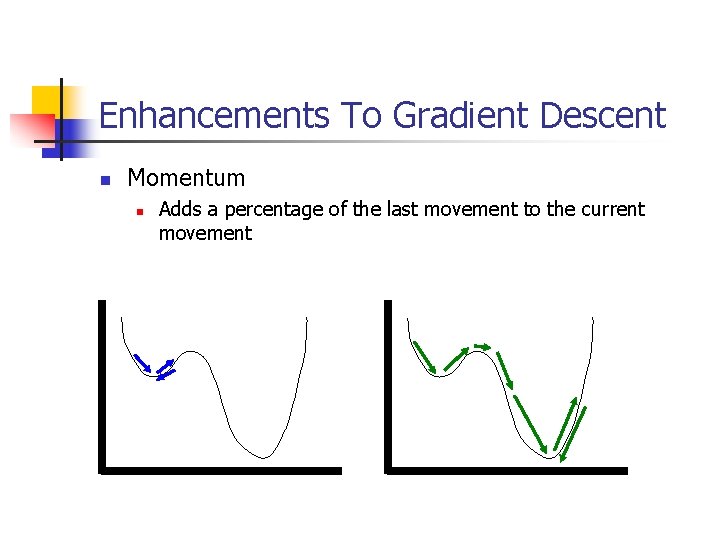
Enhancements To Gradient Descent n Momentum n Adds a percentage of the last movement to the current movement

Enhancements To Gradient Descent n Momentum n n n Useful to get over small bumps in the error function Often finds a minimum in less steps w(t) = -n*d*y + a*w(t-1) n n n w is the change in weight n is the learning rate d is the error y is different depending on which layer we are calculating a is the momentum parameter

Enhancements To Gradient Descent n Adaptive Backpropagation Algorithm n n It assigns each weight a learning rate That learning rate is determined by the sign of the gradient of the error function from the last iteration n If the signs are equal it is more likely to be a shallow slope so the learning rate is increased The signs are more likely to differ on a steep slope so the learning rate is decreased This will speed up the advancement when on gradual slopes

Enhancements To Gradient Descent n Adaptive Backpropagation n Possible Problems: n n Since we minimize the error for each weight separately the overall error may increase Solution: n Calculate the total output error after each adaptation and if it is greater than the previous error reject that adaptation and calculate new learning rates

Enhancements To Gradient Descent n Super. SAB(Super Self-Adapting Backpropagation) n n Combines the momentum and adaptive methods. Uses adaptive method and momentum so long as the sign of the gradient does not change n n This is an additive effect of both methods resulting in a faster traversal of gradual slopes When the sign of the gradient does change the momentum will cancel the drastic drop in learning rate n This allows for the function to roll up the other side of the minimum possibly escaping local minima

Enhancements To Gradient Descent n Super. SAB n n Experiments show that the Super. SAB converges faster than gradient descent Overall this algorithm is less sensitive (and so is less likely to get caught in local minima)

Other Ways To Minimize Error n Varying training data n n n Add noise to training data n n Cycle through input classes Randomly select from input classes Randomly change value of input node (with low probability) Retrain with expected inputs after initial training n E. g. Speech recognition

Other Ways To Minimize Error n Adding and removing neurons from layers n n Adding neurons speeds up learning but may cause loss in generalization Removing neurons has the opposite effect

Resources n n n Artifical Neural Networks, Backpropagation, J. Henseler Artificial Intelligence: A Modern Approach, S. Russell & P. Norvig 501 notes, J. R. Parker www. dontveter. com/bpr. html www. dse. doc. ic. ac. uk/~nd/surprise_96/journal/vl 4/cs 11/report. html