Neural Computation and Applications in Time Series and

Neural Computation and Applications in Time Series and Signal Processing Georg Dorffner Dept. of Medical Cybernetics and Artificial Intelligence, University of Vienna And Austrian Research Institute for Artificial Intelligence June 2003 Neural Computation for Time Series 1

Neural Computation • Originally biologically motivated (information processing in the brain) • Simple mathematical model of the neuron neural network • Large number of simple „units“ • Massively parallel (in theory) • Complexity through the interplay of many simple elements • Strong relationship to methods from statistics • Suitable for pattern recognition June 2003 Neural Computation for Time Series 2

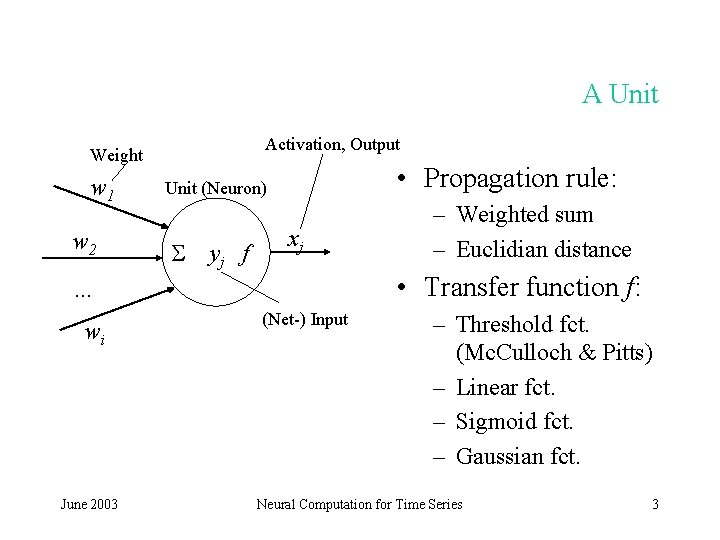
A Unit Activation, Output Weight w 1 w 2 • Propagation rule: Unit (Neuron) yj f xj • Transfer function f: … wi June 2003 – Weighted sum – Euclidian distance (Net-) Input – Threshold fct. (Mc. Culloch & Pitts) – Linear fct. – Sigmoid fct. – Gaussian fct. Neural Computation for Time Series 3

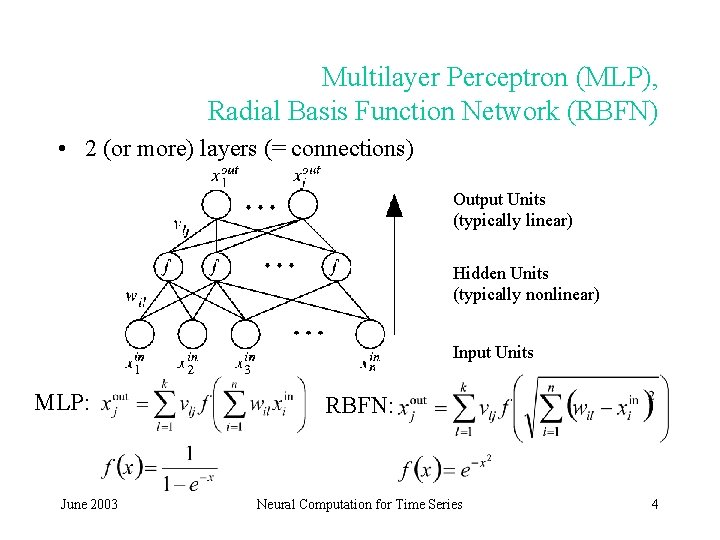
Multilayer Perceptron (MLP), Radial Basis Function Network (RBFN) • 2 (or more) layers (= connections) Output Units (typically linear) Hidden Units (typically nonlinear) Input Units MLP: June 2003 RBFN: Neural Computation for Time Series 4

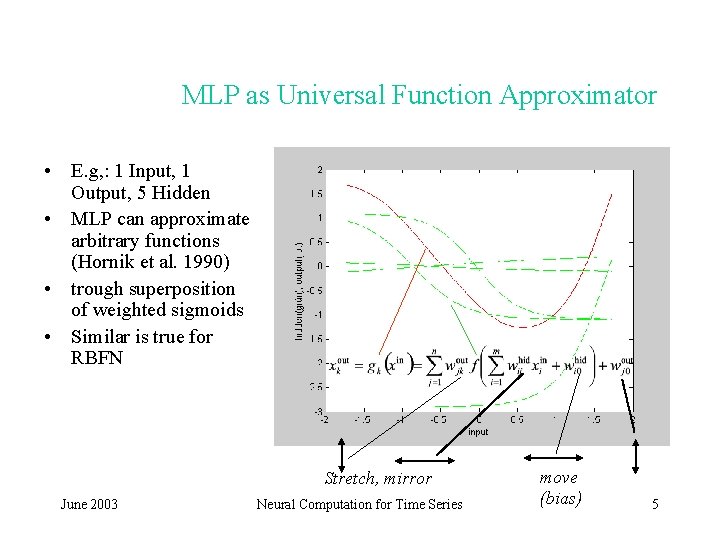
MLP as Universal Function Approximator • E. g, : 1 Input, 1 Output, 5 Hidden • MLP can approximate arbitrary functions (Hornik et al. 1990) • trough superposition of weighted sigmoids • Similar is true for RBFN Stretch, mirror June 2003 Neural Computation for Time Series move (bias) 5

Training (Model Estimation) • Iterative optimisation based on gradient (gradient descent, conjugent gradient, quasi-Newton): contribution of error function contribution of network • Typical error function: all patterns all outputs (summed squared error) target • „Backpropagation“ (application of chain rule): June 2003 Neural Computation for Time Series 6

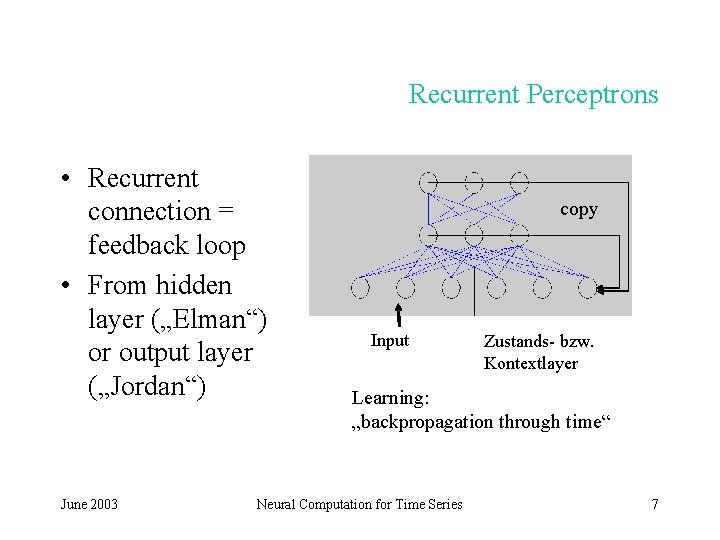
Recurrent Perceptrons • Recurrent connection = feedback loop • From hidden layer („Elman“) or output layer („Jordan“) June 2003 copy Input Zustands- bzw. Kontextlayer Learning: „backpropagation through time“ Neural Computation for Time Series 7

Time series processing • Given: time-dependent observables • Scalar: univariate; vector: multivariate • Typical tasks: - Forecasting - Noise modeling Time series (minutes to days) June 2003 - Pattern recognition - Modeling - Filtering - Source separation Signals (milliseconds to seconds) Neural Computation for Time Series 8

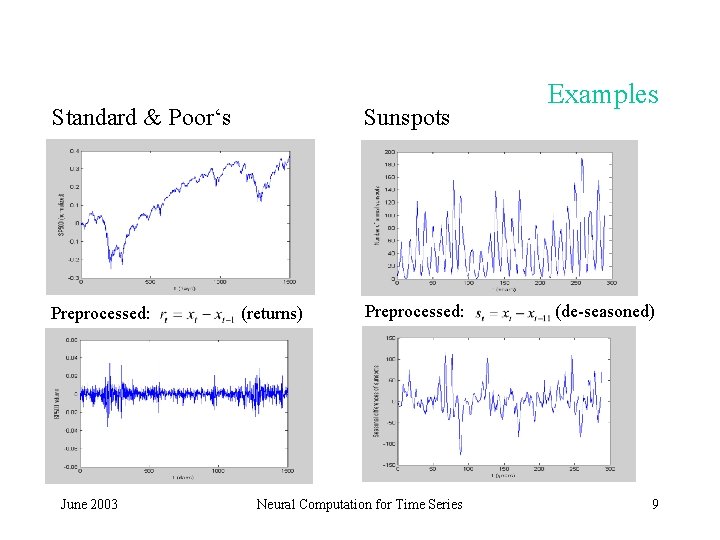
Standard & Poor‘s Preprocessed: June 2003 Sunspots Examples Preprocessed: (de-seasoned) Neural Computation for Time Series 9 (returns)

Autoregressive models • Forecasting: making use of past information to predict (estimate) the future • AR: Past information = past observations Noise, „random shock“ Expected value • Best forecast: expected value June 2003 Neural Computation for Time Series 10

Linear AR models • Most common case: • Simplest form: random walk • Nontrivial forecast impossible June 2003 Neural Computation for Time Series 11

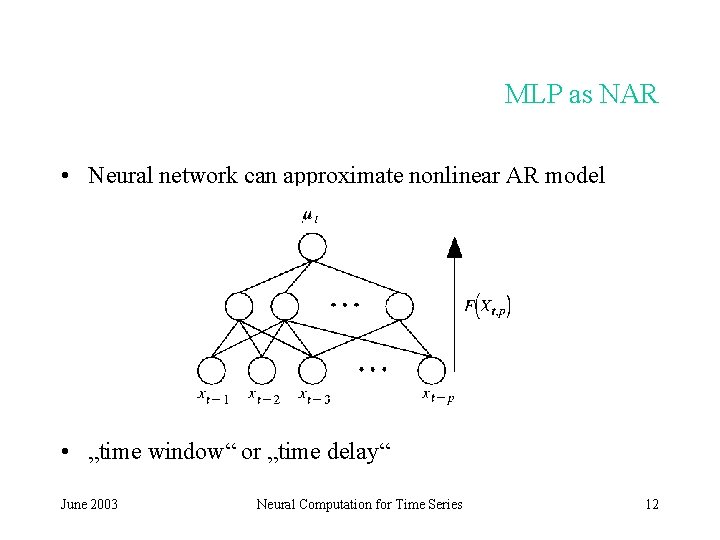
MLP as NAR • Neural network can approximate nonlinear AR model • „time window“ or „time delay“ June 2003 Neural Computation for Time Series 12

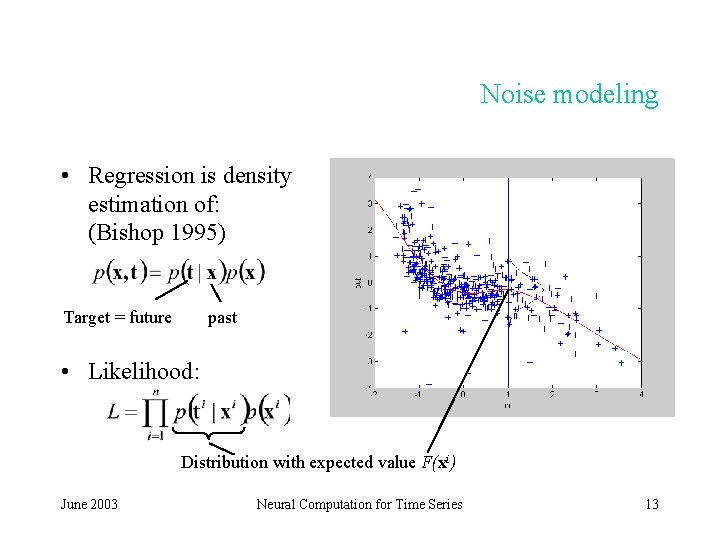
Noise modeling • Regression is density estimation of: (Bishop 1995) Target = future past • Likelihood: Distribution with expected value F(xi) June 2003 Neural Computation for Time Series 13

Gaussian noise • Likelihood: • Maximization = minimization of -log. L (constant terms can be deleted, incl. p(x)) • Corresponds to summed squared error (typical backpropagation) June 2003 Neural Computation for Time Series 14

Complex noise models • Assumption: arbitrary distribution • Parameters are time dependent (dependent on past): • Likelihood: Probability density function for D June 2003 Neural Computation for Time Series 15

Heteroskedastic time series • Assumption: Noise is Gaussian with time-dependent variance • ARCH model • MLP is nonlinear ARCH (when applied to returns/residuals) June 2003 Neural Computation for Time Series 16

Non-Gaussian noise • Other parametric pdfs (e. g. t-distribution) • Mixture of Gaussians (Mixture density network, Bishop 1994) • Network with 3 k outputs (or separate networks) June 2003 Neural Computation for Time Series 17

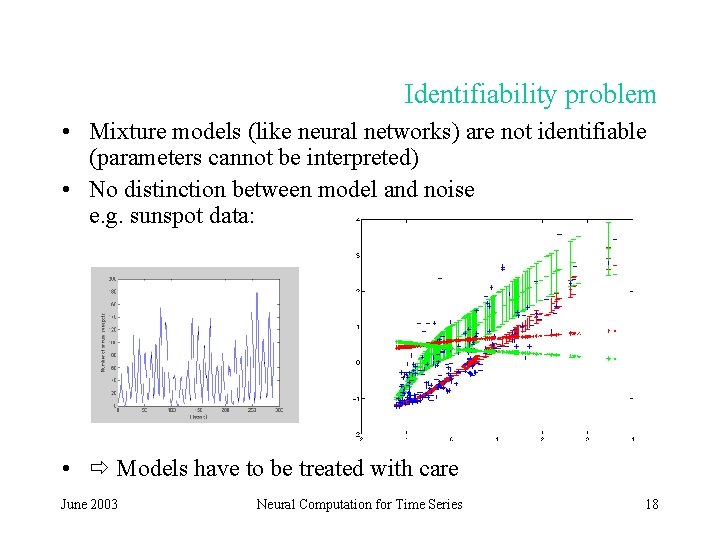
Identifiability problem • Mixture models (like neural networks) are not identifiable (parameters cannot be interpreted) • No distinction between model and noise e. g. sunspot data: • Models have to be treated with care June 2003 Neural Computation for Time Series 18

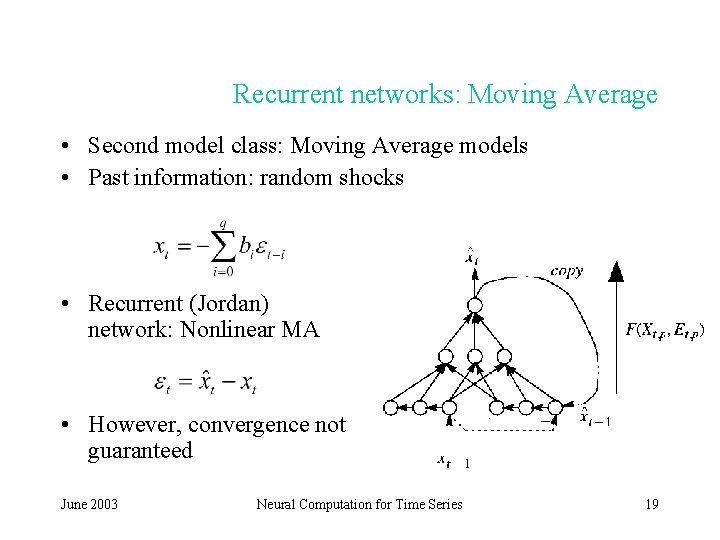
Recurrent networks: Moving Average • Second model class: Moving Average models • Past information: random shocks • Recurrent (Jordan) network: Nonlinear MA • However, convergence not guaranteed June 2003 Neural Computation for Time Series 19

GARCH • Extension of ARCH: • Explains „volatility clustering“ • Neural network can again be a nonlinear version • Using past estimates: recurrent network June 2003 Neural Computation for Time Series 20

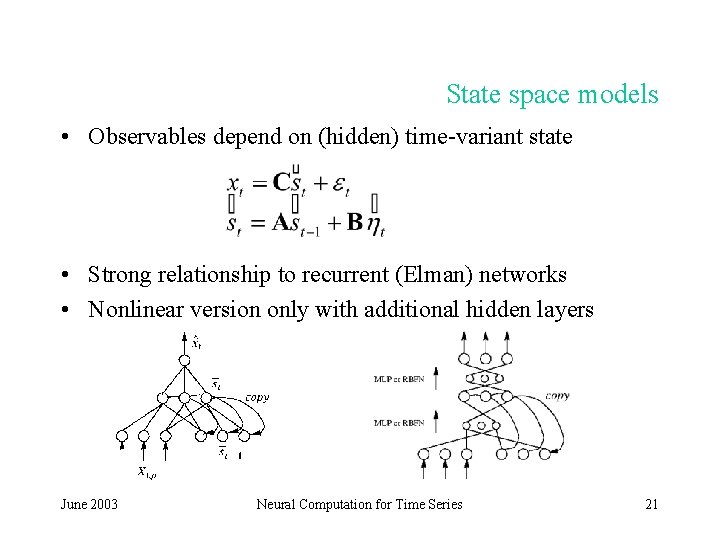
State space models • Observables depend on (hidden) time-variant state • Strong relationship to recurrent (Elman) networks • Nonlinear version only with additional hidden layers June 2003 Neural Computation for Time Series 21

Symbolic time series • Examples: alphabet – DNA – Text – Quantised time series (e. g. „up“ and „down“) • Past information: past p symbols probability distribution • Markov chains • Problem: long substrings are rare June 2003 Neural Computation for Time Series 22

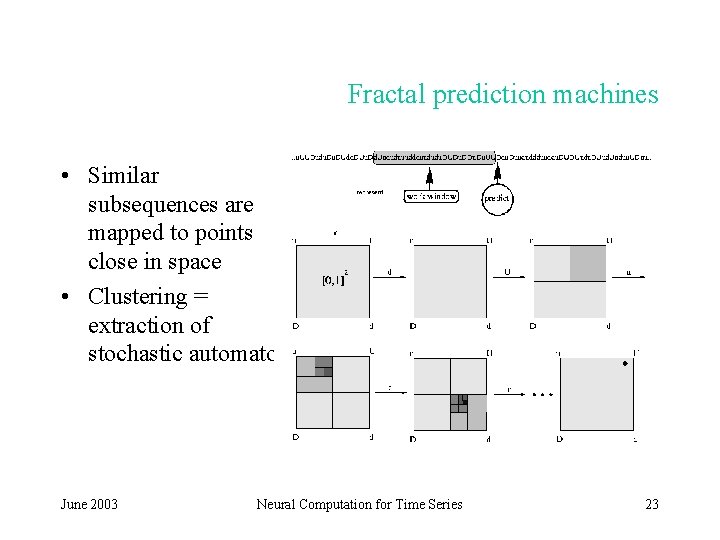
Fractal prediction machines • Similar subsequences are mapped to points close in space • Clustering = extraction of stochastic automaton June 2003 Neural Computation for Time Series 23

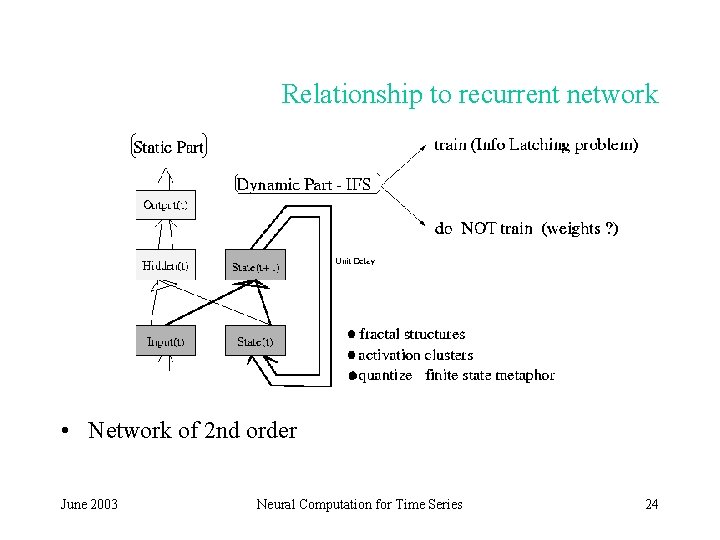
Relationship to recurrent network • Network of 2 nd order June 2003 Neural Computation for Time Series 24

Other topics • Filtering: corresponds to ARMA models NN as nonlinear filters • Source separation independent component analysis • Relationship to stochastic automata June 2003 Neural Computation for Time Series 25

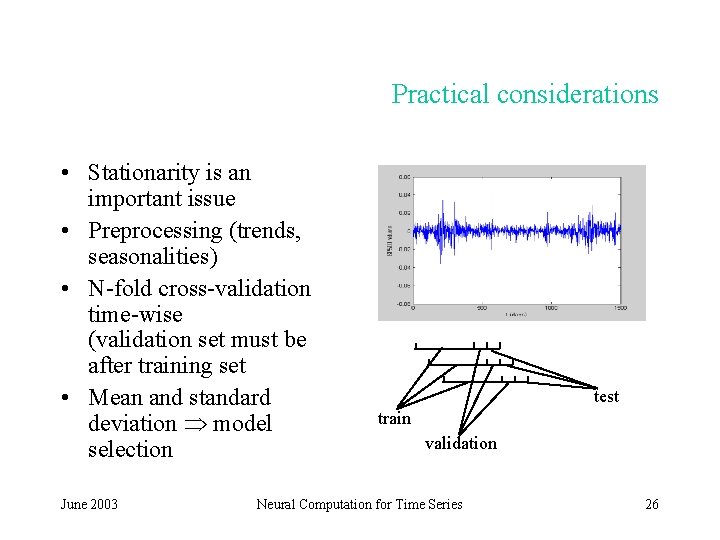
Practical considerations • Stationarity is an important issue • Preprocessing (trends, seasonalities) • N-fold cross-validation time-wise (validation set must be after training set • Mean and standard deviation model selection June 2003 test train validation Neural Computation for Time Series 26

Summary • Neural networks are powerful semi-parametric models for nonlinear dependencies • Can be considered as nonlinear extensions of classical time series and signal processing techniques • Applying semi-parametric models to noise modeling adds another interesting facet • Models must be treated with care, much data necessary June 2003 Neural Computation for Time Series 27