Network Theorems Circuit analysis Mesh analysis n Nodal

Network Theorems

Circuit analysis Mesh analysis n Nodal analysis n Superposition n Thevenin’s Theorem n Norton’s Theorem n Delta-star transformation n

n n n An active network having two terminals A and B can be replaced by a constant-voltage source having an e. m. f Vth and an internal resistance Rth. The value of Vth is equal to the open-circuited p. d between A and B. The value of Rth is the resistance of the network measured between A and B with the load disconnected and the sources of e. m. f replaced by their internal resistances.

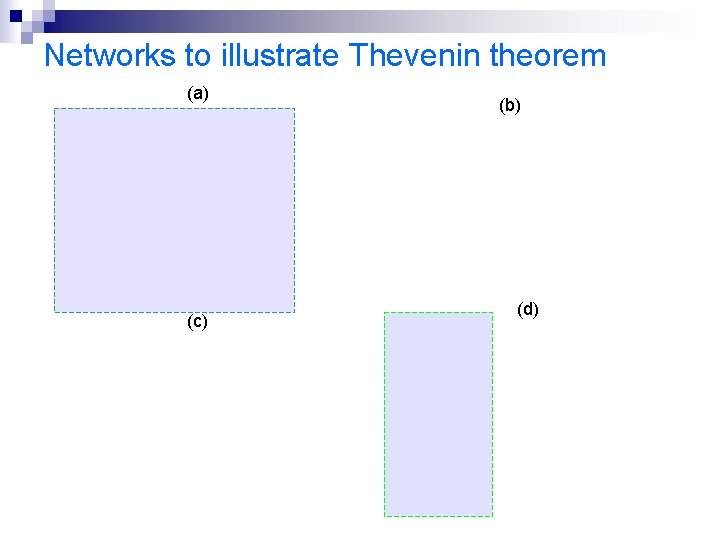
Networks to illustrate Thevenin theorem (a) (c) (b) (d)

Refer to network (b), in R 2 there is not complete circuit, thus no current, thus current in R 3 And p. d across R 3 is Since no current in R 2, thus Refer to network (c) the resistance at AB Thus current in R (refer network (d))

Calculate the current through R 3 Solution With R 3 disconnected as in figure below p. d across CD is E 1 -I 1 R 1

continue To determine the internal resistance we remove the e. m. f s Replace the network with V=5. 2 V and r=1. 2, then the at terminal CD, R 3, thus the current

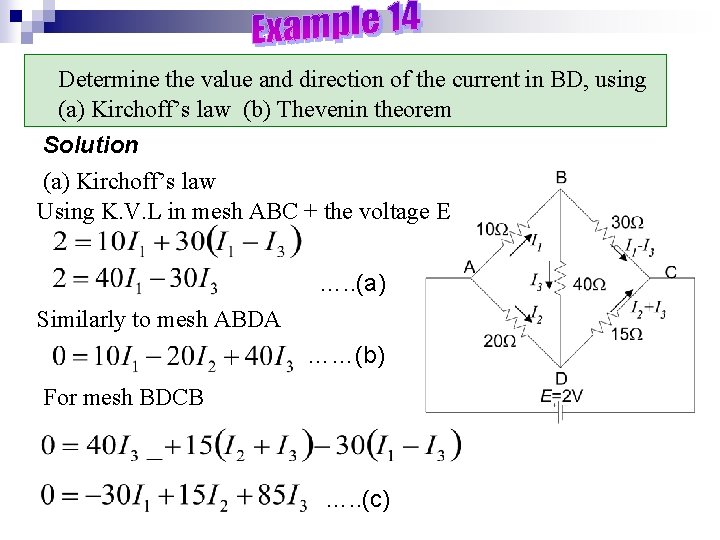
Determine the value and direction of the current in BD, using (a) Kirchoff’s law (b) Thevenin theorem Solution (a) Kirchoff’s law Using K. V. L in mesh ABC + the voltage E …. . (a) Similarly to mesh ABDA ……(b) For mesh BDCB …. . (c)

Continue…… Multiplying (b) by 3 and (c) by 4 and adding the two expressions, thus Substitute I 1 in (a) Since the I 3 is positive then the direction in the figure is correct.

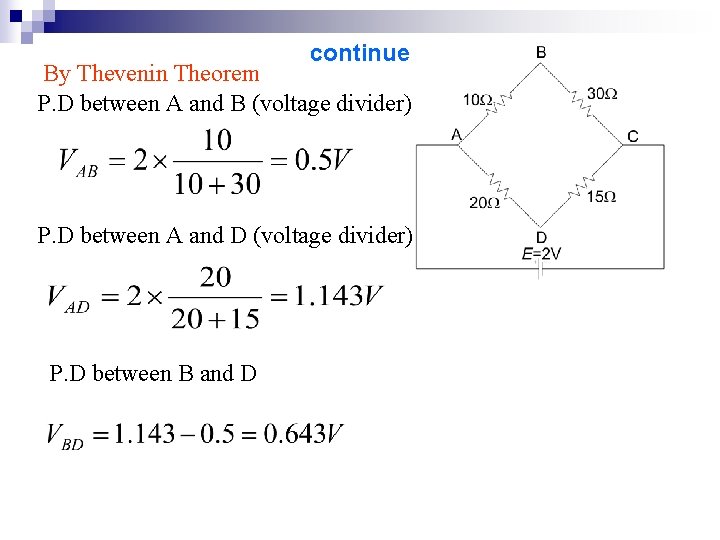
continue By Thevenin Theorem P. D between A and B (voltage divider) P. D between A and D (voltage divider) P. D between B and D

For effective resistance, 10 parallel to 30 continue 20 parallel to 15 Total Substitute the voltage, resistance r and 10 W as in figure below

Another of expressing the current IL Where IS=E/RS is the current would flow in a short circuit across the source terminal( i. e when RL is replaced by short circuit) Then we can represent the voltage source as equivalent current source

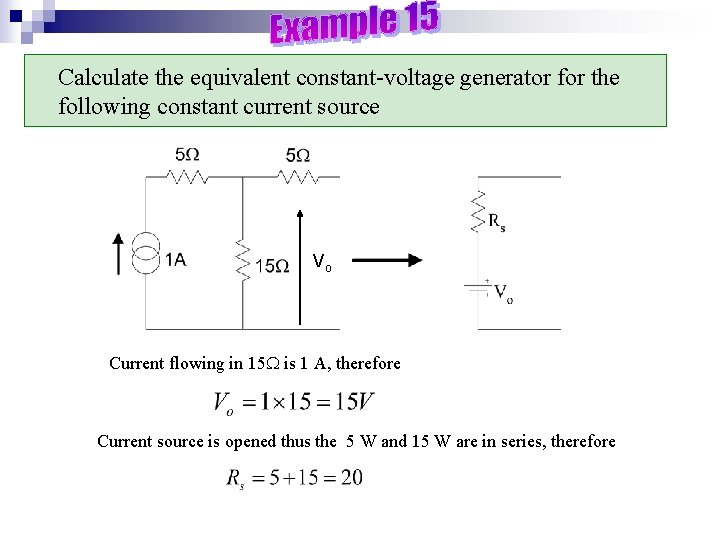
Calculate the equivalent constant-voltage generator for the following constant current source Vo Current flowing in 15 is 1 A, therefore Current source is opened thus the 5 W and 15 W are in series, therefore

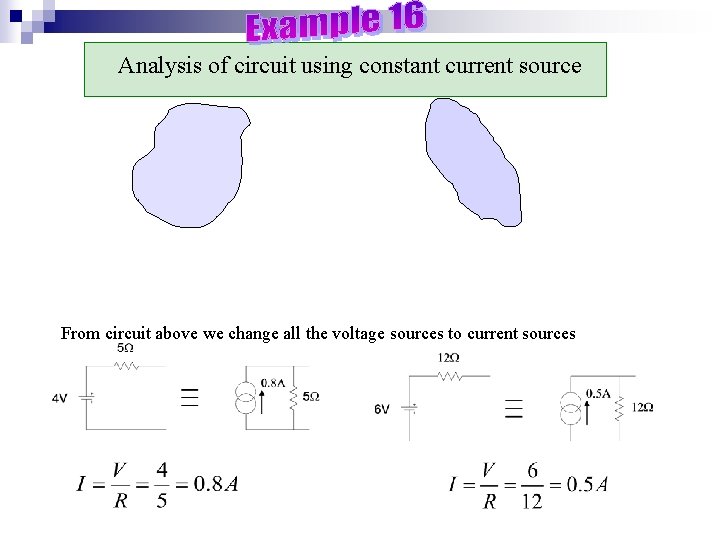
Analysis of circuit using constant current source From circuit above we change all the voltage sources to current sources

continue At node 1 At node 2 X 120 X 30 …. . (a) ……(b)

continue ………( c ) (c) + (b) From (a) Hence the current in the 8 is So the answers are same as before

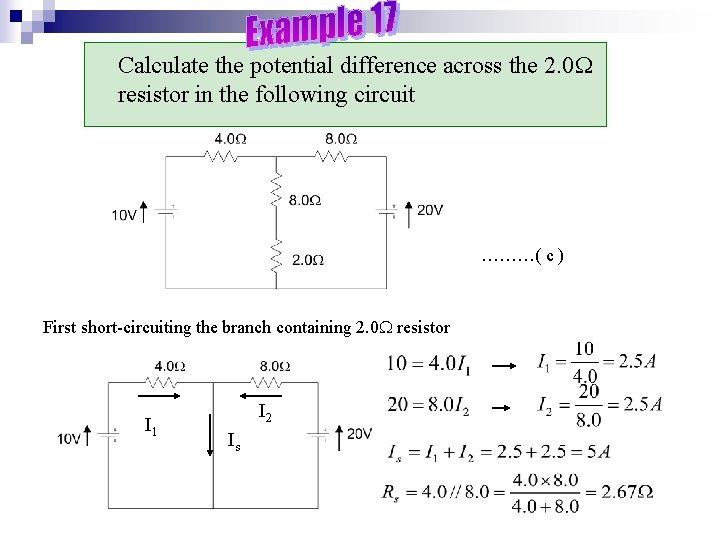
Calculate the potential difference across the 2. 0 resistor in the following circuit ………( c ) First short-circuiting the branch containing 2. 0 resistor I 1 I 2 Is

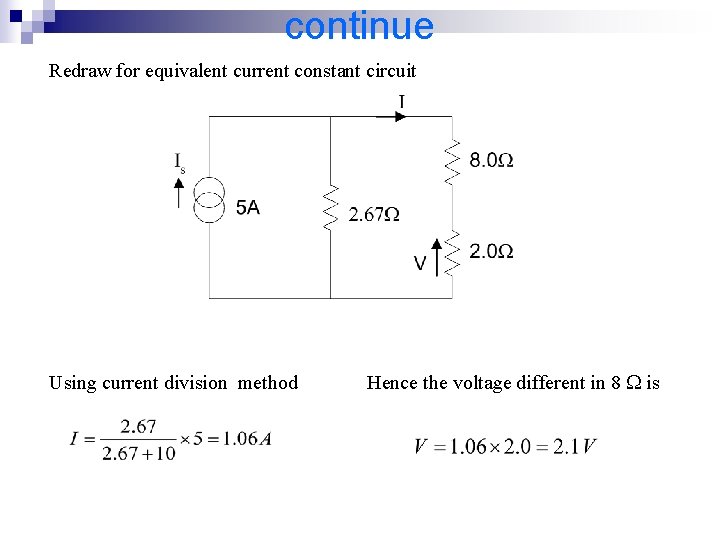
continue Redraw for equivalent current constant circuit Using current division method Hence the voltage different in 8 is

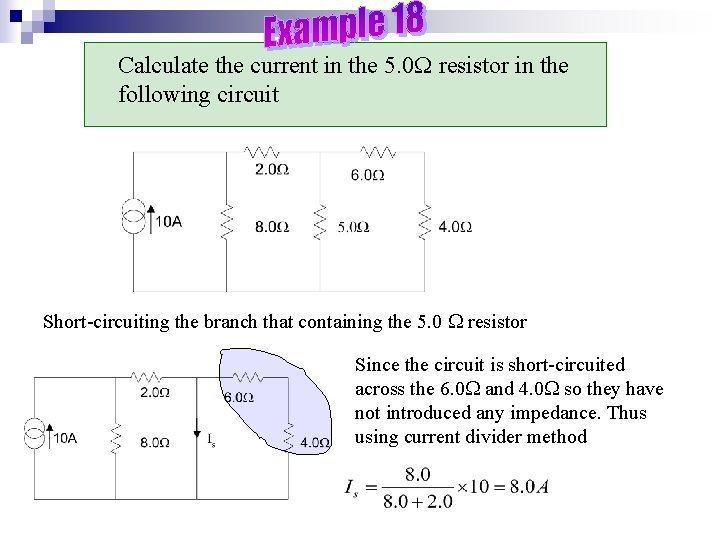
Calculate the current in the 5. 0 resistor in the following circuit Short-circuiting the branch that containing the 5. 0 resistor Since the circuit is short-circuited across the 6. 0 and 4. 0 so they have not introduced any impedance. Thus using current divider method

continue The equivalent resistance is a parallel (2. 0+8. 0)//(6. 0+4. 0) Redraw the equivalent constant current circuit with the load 5. 0 I Hence the current in the 5 is

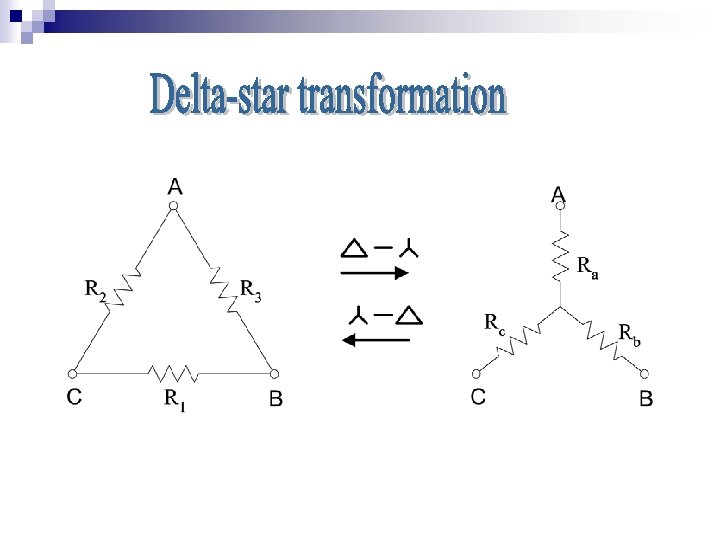
Delta to star transformation From delta cct , impedance sees from AB From star cct , impedance sees from AB Thus equating (a) Similarly from BC (b) and from AC (c) (b) – (c) (d) By adding (a) and (d) ; (b) and (d) ; and (c) and (d) and then divided by two yield (f) (e) (g)

Delta to star transformation Dividing (e) by (f) therefore Similarly, dividing (e) by (g) We have Substitude R 2 and R 3 into (e) Similarly (i) (j) (k) (l) (m) (n)

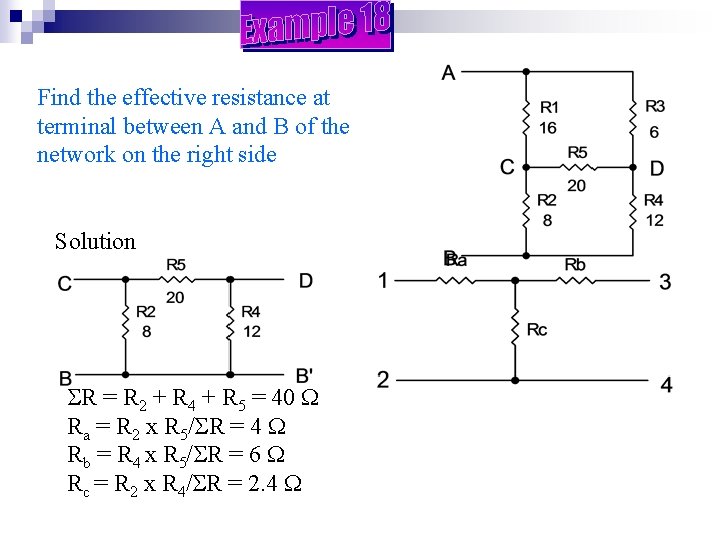
Find the effective resistance at terminal between A and B of the network on the right side Solution R = R 2 + R 4 + R 5 = 40 Ra = R 2 x R 5/ R = 4 Rb = R 4 x R 5/ R = 6 Rc = R 2 x R 4/ R = 2. 4

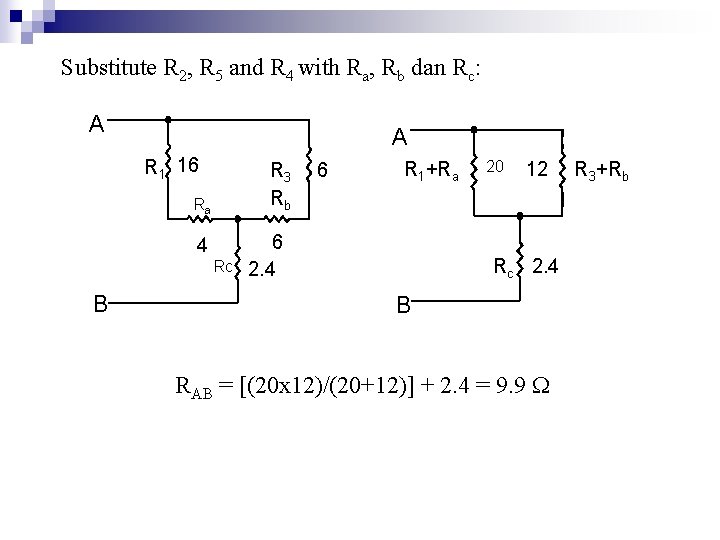
Substitute R 2, R 5 and R 4 with Ra, Rb dan Rc: A A R 1 16 R 3 Rb Ra 4 Rc B 6 R 1+Ra 6 2. 4 20 12 Rc 2. 4 B RAB = [(20 x 12)/(20+12)] + 2. 4 = 9. 9 R 3+Rb