Network teleology Damon Wischik http www cs ucl

Network teleology Damon Wischik http: //www. cs. ucl. ac. uk/staff/D. Wischik/Talks/teleology. html

What is teleology? • Teleology (noun). The doctrine or study of ends or final causes, especially as related to the evidences of design or purpose in nature; also transf. such design as exhibited in natural objects or phenomena. – Greek teleo- from telo , end

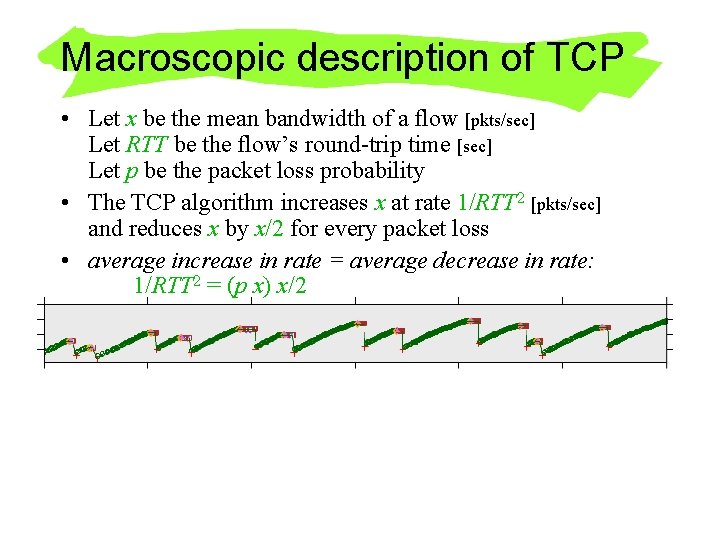
Macroscopic description of TCP • Let x be the mean bandwidth of a flow [pkts/sec] Let RTT be the flow’s round-trip time [sec] Let p be the packet loss probability • The TCP algorithm increases x at rate 1/RTT 2 [pkts/sec] and reduces x by x/2 for every packet loss • average increase in rate = average decrease in rate: 1/RTT 2 = (p x) x/2

Macroscopic description • Let x be the mean bandwidth of a flow [pkts/sec] Let RTT be the flow’s round-trip time [sec] Let p be the packet loss probability • The TCP algorithm increases x at rate 1/RTT 2 [pkts/sec] and reduces x by x/2 for every packet loss • average increase in rate = average decrease in rate: 1/RTT 2 = (p x) x/2 • Consider a link with N identical flows Let NC be the capacity of the link [pkts/sec] • packet loss ratio = fraction of work that exceeds service rate: p = (Nx-NC)+/Nx = (x-C)+/x

Teleological description U(x) P(y, C) • Consider several TCP flows sharing a single link • Let xr be the mean bandwidth of flow r [pkts/sec] Let y be the total bandwidth of all flows [pkts/sec] Let C be the total available capacity [pkts/sec] • TCP and the network act so as to solve maximise år U(xr) - P(y, C) over xr 0 where y=år xr x C y

U(x) Teleological description severe penalty for allocating too little bandwidth little extra valued attached to highbandwidth flows x

Teleological description U(x) flows with large RTT are satisfied with little bandwidth flows with small RTT want more bandwidth x

P(y, C) Teleological description no penalty unless links are overloaded C y

Teleological description U(x) P(y, C) • The network distributes resources as if it’s solving an optimization problem • Is this what we want the Internet to optimize? • Does it make good use of the network? • Can it deliver high bandwidth and good quality? • Is it a fair allocation? • Can we design a better allocation? x C y

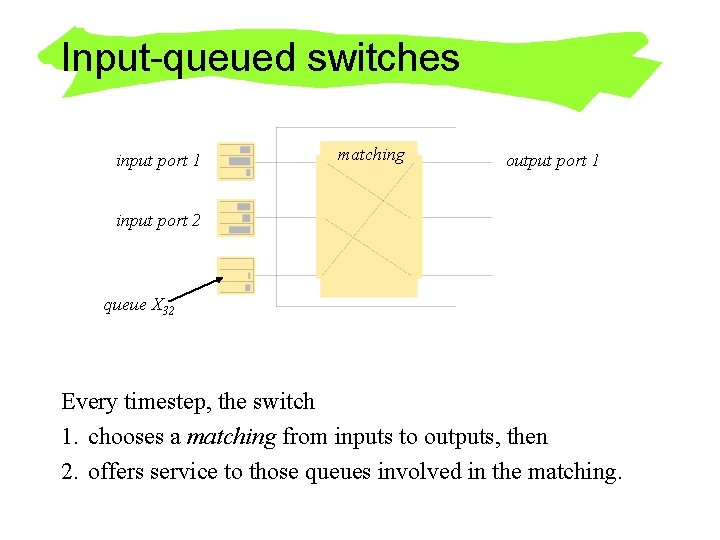
Input-queued switches input port 1 matching output port 1 input port 2 queue X 32 Every timestep, the switch 1. chooses a matching from inputs to outputs, then 2. offers service to those queues involved in the matching.

The MWM matching algorithm • How does the switch decide which matching to use? • Let the weight of a matching p be p·X = åi, j Xi j pi j • Let the maximum weight be maxp p·X • The MWM (Maximum Weight Matching) algorithm chooses, at every time step, some matching which achieves the maximum weight.

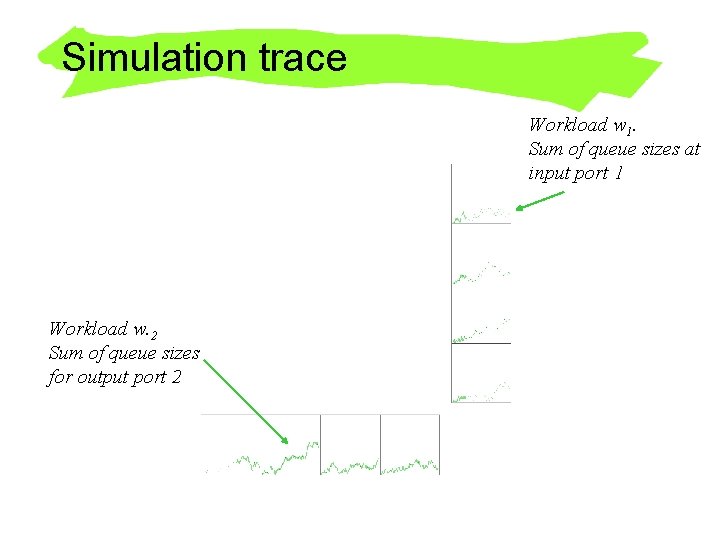
queue lengths [0 -50 pkts] Simulation trace time [0 -500]

Simulation trace Workload w 1. Sum of queue sizes at input port 1 Workload w. 2 Sum of queue sizes for output port 2

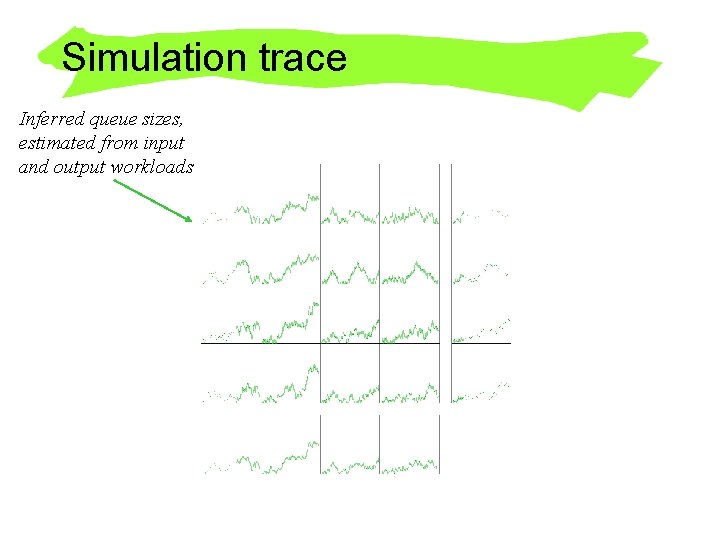
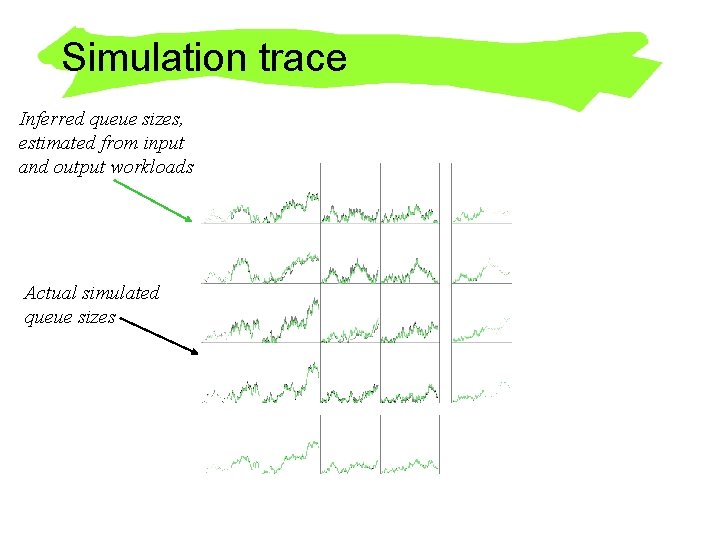
Simulation trace Inferred queue sizes, estimated from input and output workloads

Simulation trace Inferred queue sizes, estimated from input and output workloads Actual simulated queue sizes

Teleological description • The switching algorithm distributes the workload among the input queues so as to solve an optimization problem • Is this an optimization problem we want to solve? • Would a different switching algorithm reduce the buffer overflow probability?

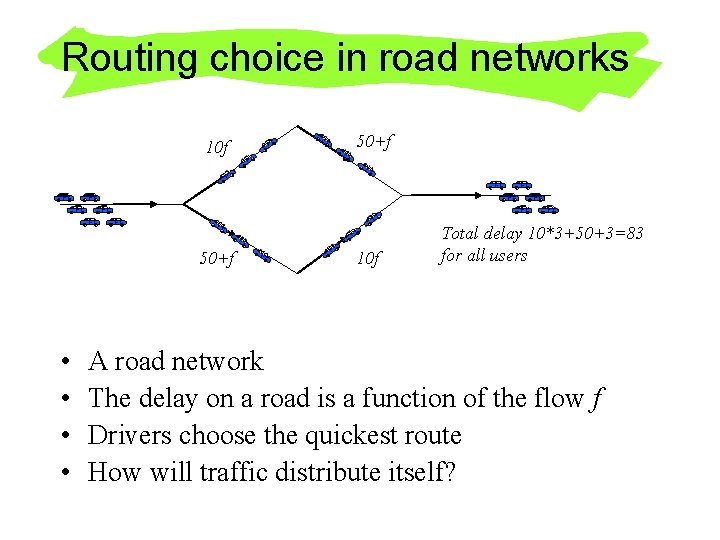
Routing choice in road networks 10 f 50+f • • 50+f 10 f Total delay 10*3+50+3=83 for all users A road network The delay on a road is a function of the flow f Drivers choose the quickest route How will traffic distribute itself?

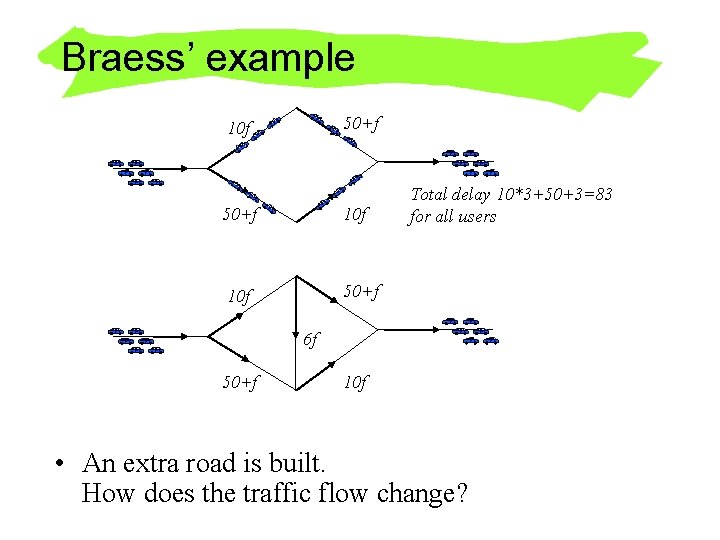
Braess’ example 50+f 10 f 10 f 50+f Total delay 10*3+50+3=83 for all users 6 f 50+f 10 f • An extra road is built. How does the traffic flow change?

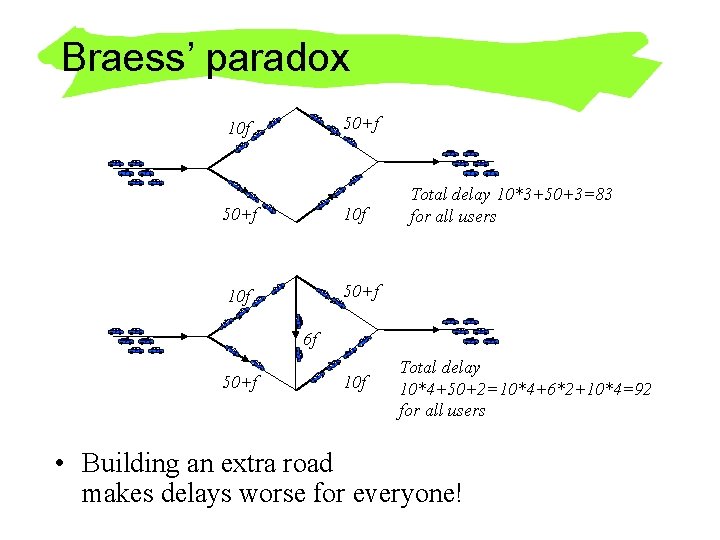
Braess’ paradox 50+f 10 f 10 f 50+f Total delay 10*3+50+3=83 for all users 6 f 50+f 10 f Total delay 10*4+50+2=10*4+6*2+10*4=92 for all users • Building an extra road makes delays worse for everyone!

Wardrop equilibrium • The allocation of flows satisfies an optimization problem • The objective function is not the natural one (i. e. minimize average delay) • How can we encourage drivers to choose socially optimal routes?

Conclusion • A network algorithm is usually specified at the microscopic level (i. e. by code) • The code may have an implicit teleology • The teleological view can – give insight into the algorithm – suggest tweaks