Network Parameters Impedance and Admittance matrices For n

Network Parameters

Impedance and Admittance matrices For n ports network we can relate the voltages and currents by impedance and admittance matrices Impedance matrix where Admittance matrix

Reciprocal and Lossless Networks Reciprocal networks usually contain nonreciprocal media such as ferrites or plasma, or active devices. We can show that the impedance and admittance matrices are symmetrical, so that. Lossless networks can be shown that Zij or Yij are imaginary Refer to text book Pozar pg 193 -195

Example Find the Z parameters of the two-port T –network as shown below I 1 I 2 V 1 V 2 Solution Port 2 open-circuited Port 1 open-circuited Similarly we can show that This is an example of reciprocal network!!

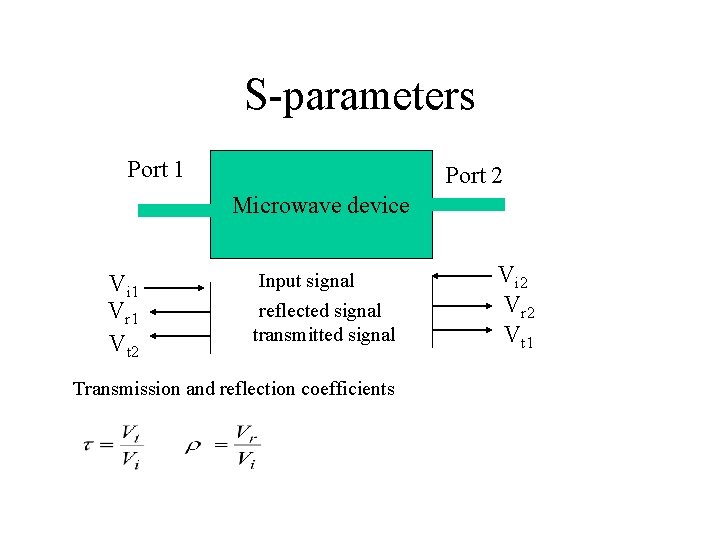
S-parameters Port 1 Port 2 Microwave device Vi 1 Vr 1 Vt 2 Input signal reflected signal transmitted signal Transmission and reflection coefficients Vi 2 Vr 2 Vt 1

S-parameters Voltage of traveling wave away from port 1 is Voltage of Reflected wave From port 1 Voltage of Transmitted wave From port 2 Voltage of transmitted wave away from port 2 is Let Vb 1= b 1 , Vi 1=a 1 , Vi 2=a 2 , Then we can rewrite

S-parameters Hence In matrix form S-matrix • S 11 and S 22 are a measure of reflected signal at port 1 and port 2 respectively • S 21 is a measure of gain or loss of a signal from port 1 to port 2. • S 12 ia a measure of gain or loss of a signal from port 2 to port 1. Logarithmic form S 11=20 log(r 1) S 22=20 log(r 2) S 12=20 log(t 12) S 21=20 log(t 21)

S-parameters Vr 2=0 means port 2 is matched Vr 1=0 means port 1 is matched

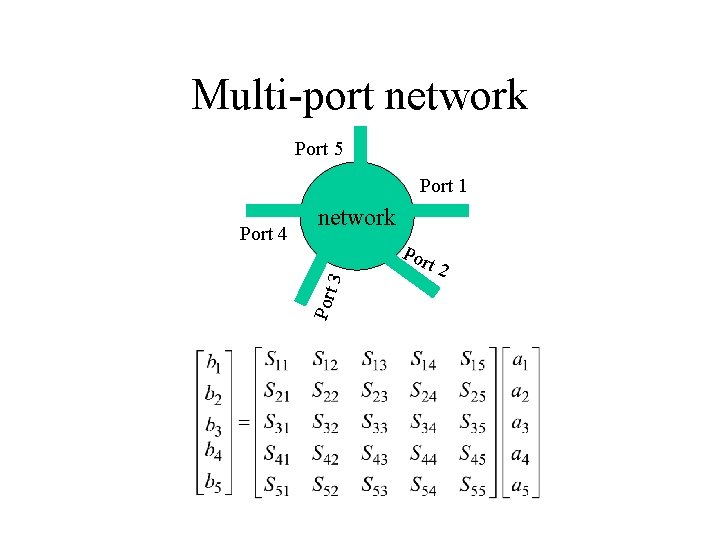
Multi-port network Port 5 Port 1 3 Port 4 network t 2

Example Below is a matched 3 d. B attenuator. Find the S-parameter of the circuit. Z 1=Z 2= 8. 56 W and Z 3= 141. 8 W Solution By assuming the output port is terminated by Zo = 50 W, then Because of symmetry , then S 22=0

Continue V 1 Vo From the fact that S 11=S 22=0 , we know that Vr 1=0 when port 2 is matched, and that Vi 2=0. Therefore Vi 1= V 1 and Vt 2=V 2 Therefore S 12 = S 21 = 0. 707 V 2

Lossless network For lossless n-network , total input power = total output power. Thus Where a and b are the amplitude of the signal Putting in matrix form Thus at (I – St S* In summation form )a* at a* = bt b* =at St S* a* =0 This implies that Note that bt=at. St and b*=S*a* St S* =I Called unitary matrix

Conversion of Z to S and S to Z where

Reciprocal and symmetrical network Since the [U] is diagonal , thus For reciprocal network Since [Z] is symmetry Thus it can be shown that

Example A certain two-port network is measured and the following scattering matrix is obtained: From the data , determine whether the network is reciprocal or lossless. If a short circuit is placed on port 2, what will be the resulting return loss at port 1? Solution Since [S] is symmetry, the network is reciprocal. To be lossless, the S parameters must satisfy For i=j |S 11|2 + |S 12|2 = (0. 1)2 + (0. 8)2 = 0. 65 Since the summation is not equal to 1, thus it is not a lossless network.

continue Reflected power at port 1 when port 2 is shorted can be calculated as follow and the fact that a 2= -b 2 for port 2 being short circuited, thus b 1=S 11 a 1 + S 12 a 2 = S 11 a 1 - S 12 b 2 (1) b 2=S 21 a 1 + S 22 a 2 = S 21 a 1 - S 22 b 2 (2) Short at port 2 From (2) we have (3) Dividing (1) by a 1 and substitute the result in (3) , we have Return loss a 2 -a 2=b 2

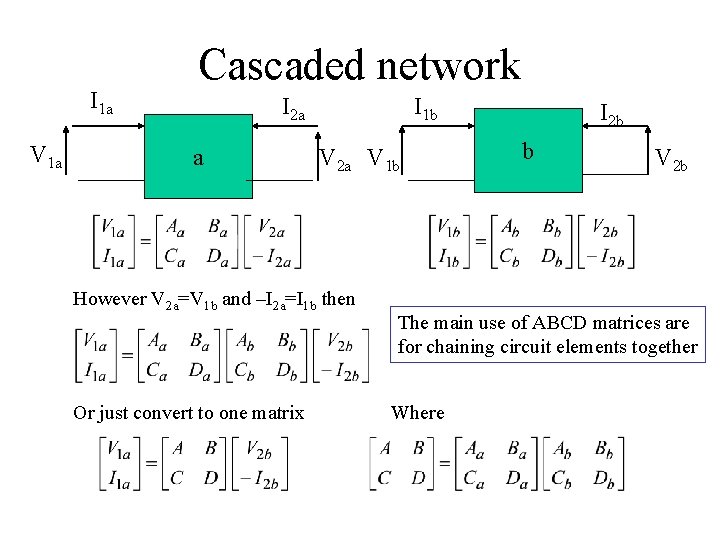
ABCD parameters I 1 V 1 I 2 Network V 2 Voltages and currents in a general circuit In matrix form This can be written as Or A –ve sign is included in the definition of D Given V 1 and I 1, V 2 and I 2 can be determined if ABDC matrix is known.

I 1 a V 1 a Cascaded network I 2 a a I 1 b V 2 a V 1 b However V 2 a=V 1 b and –I 2 a=I 1 b then Or just convert to one matrix I 2 b b V 2 b The main use of ABCD matrices are for chaining circuit elements together Where

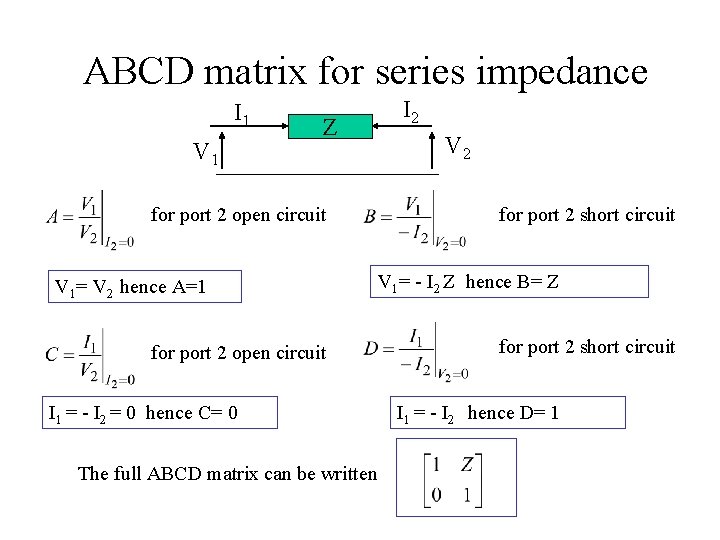
Determination of ABCD parameters Because A is independent of B, to determine A put I 2 equal to zero and determine the voltage gain V 1/V 2=A of the circuit. In this case port 2 must be open circuit. for port 2 open circuit for port 2 short circuit

ABCD matrix for series impedance I 1 V 1 Z for port 2 open circuit V 1= V 2 hence A=1 for port 2 open circuit I 1 = - I 2 = 0 hence C= 0 The full ABCD matrix can be written I 2 V 2 for port 2 short circuit V 1= - I 2 Z hence B= Z for port 2 short circuit I 1 = - I 2 hence D= 1

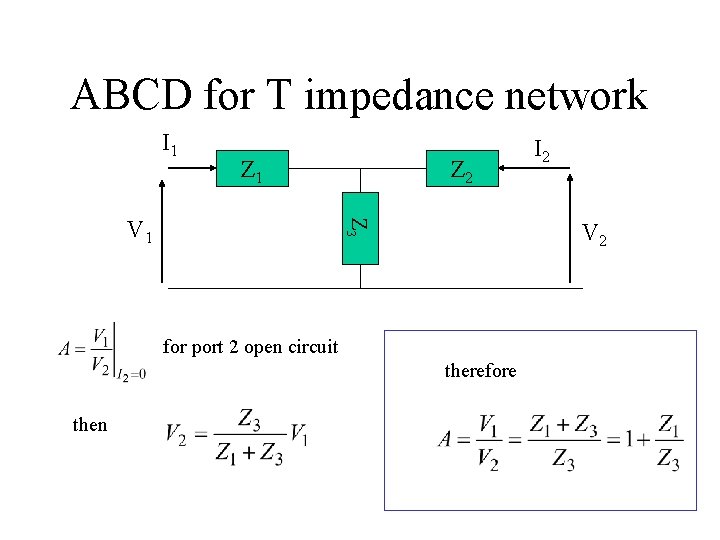
ABCD for T impedance network I 1 Z 3 V 1 Z 2 V 2 for port 2 open circuit therefore then I 2

Continue Z 1 for port 2 short circuit Solving for voltage in Z 2 Z 3 Hence But I 2 Z 2 VZ 2

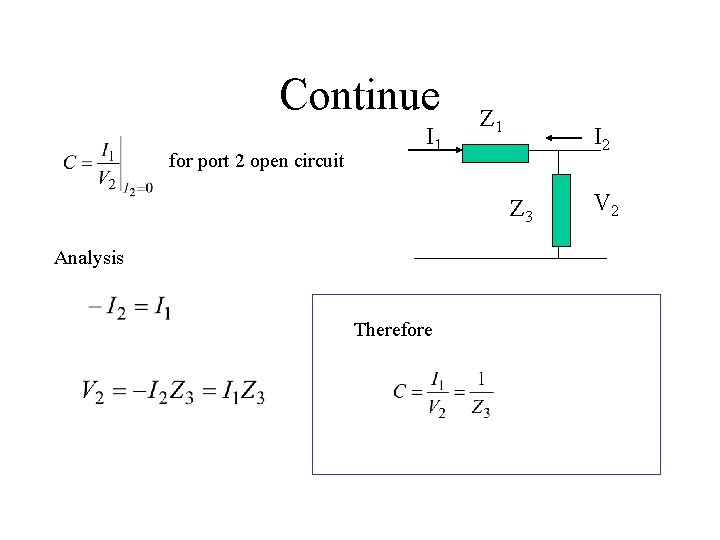
Continue for port 2 open circuit I 1 Z 1 I 2 Z 3 Analysis Therefore V 2

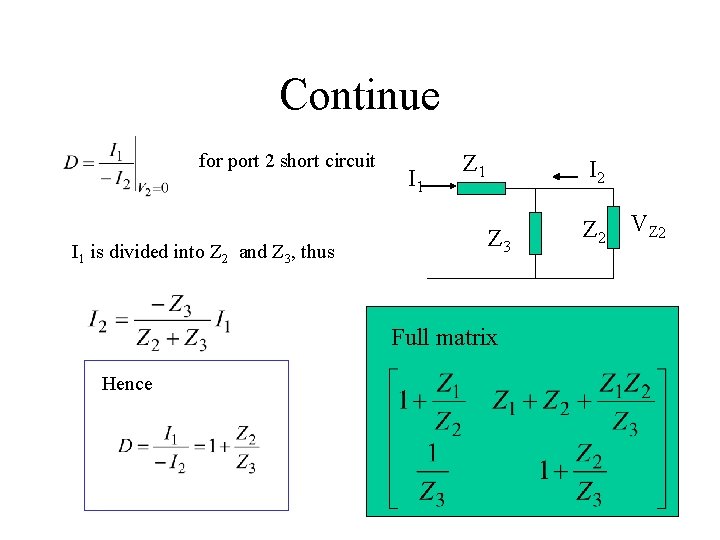
Continue for port 2 short circuit I 1 is divided into Z 2 and Z 3, thus I 1 Z 1 I 2 Z 3 Full matrix Hence Z 2 VZ 2

ABCD for transmission line I 1 Input V 1 I 2 Transmission line z=- Zo g V 2 z =0 For transmission line f and b represent forward and backward propagation voltage and current Amplitudes. The time varying term can be dropped in further analysis.

continue At the input z = - (1) (2) (3) (4) At the output z = 0 Now find A, B, C and D using the above 4 equations for port 2 open circuit For I 2 =0 Eq. ( 4 ) gives Vf= Vb=Vo giving

continue From Eq. (1) and (3) we have Note that for port 2 short circuit For V 2 = 0 , Eq. (3) implies –Vf= Vb = Vo. From Eq. (1) and (4) we have

continue for port 2 open circuit For I 2=0 , Eq. (4) implies Vf = Vb = Vo. From Eq. (2) and (3) we have for port 2 short circuit For V 2=0 , Eq. (3) implies Vf = -Vb = Vo. From Eq. (2) and (4) we have

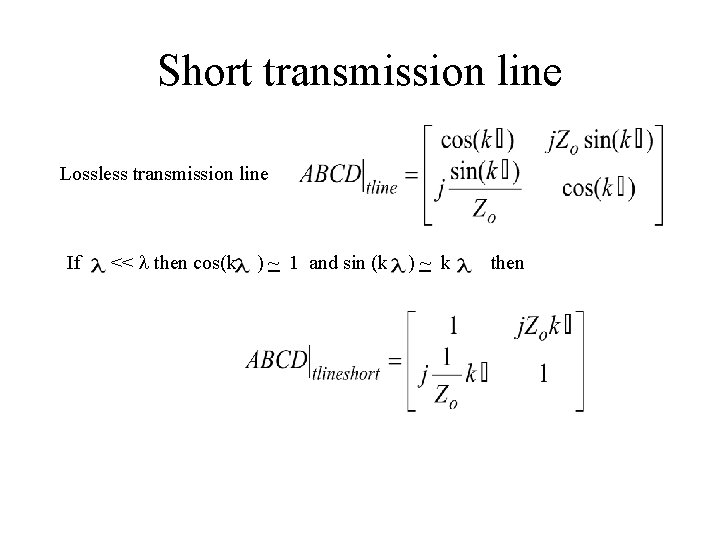
continue The complete matrix is therefore When the transmission line is lossless this reduces to Note that Where a= attenuation k=wave propagation constant Lossless line a=0

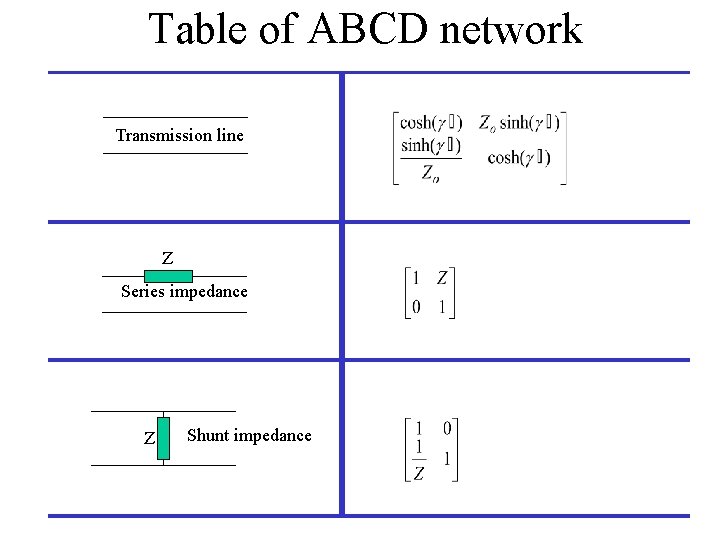
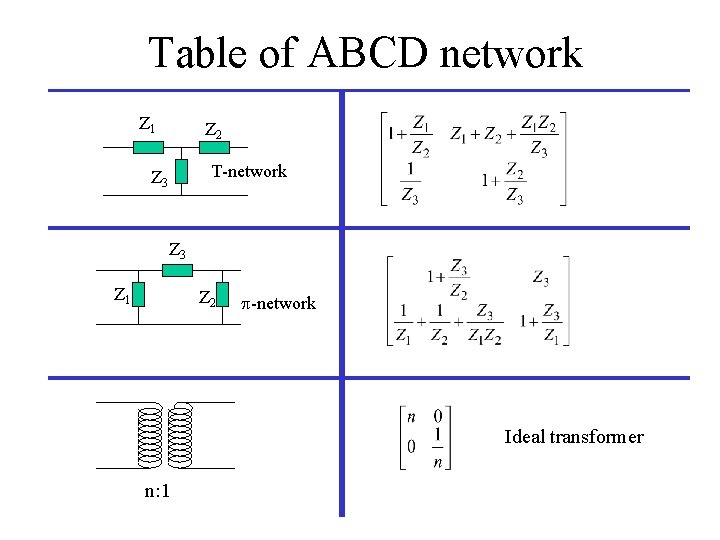
Table of ABCD network Transmission line Z Series impedance Z Shunt impedance

Table of ABCD network Z 1 Z 2 T-network Z 3 Z 1 Z 2 p-network Ideal transformer n: 1

Short transmission line Lossless transmission line If << l then cos(k ) ~ 1 and sin (k )~ k then

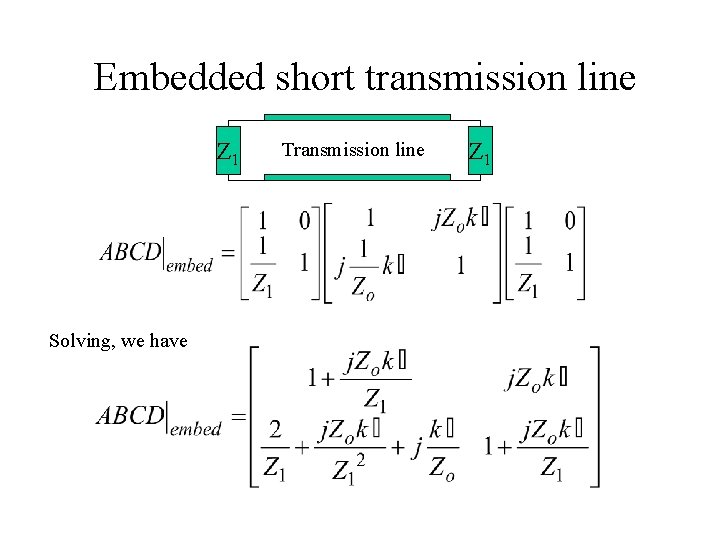
Embedded short transmission line Z 1 Solving, we have Transmission line Z 1

Comparison with p-network It is interesting to note that if we substitute in ABCD matrix in p-network, Z 2=Z 1 and Z 3=j. Zok we see that the difference is in C element where we have extra term i. e Both are almost same if So the transmission line exhibit a p-network

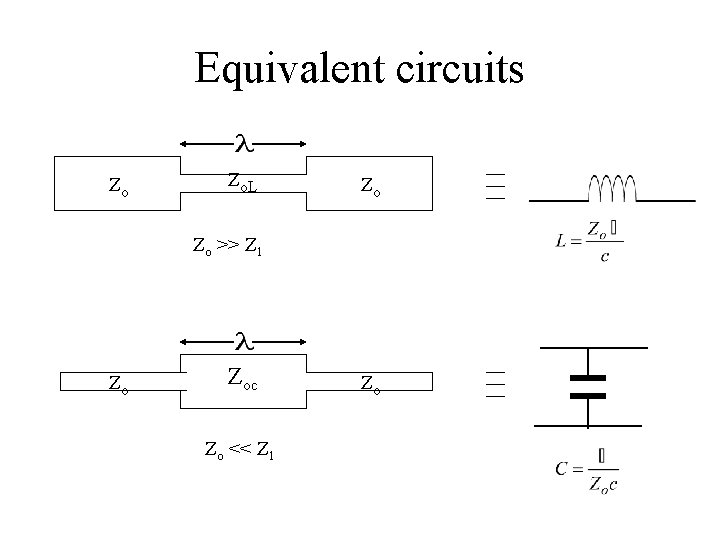
Comparison with series and shunt Series If Zo >> Z 1 then the series impedance This is an inductance which is given by Where c is a velocity of light Shunt If Zo << Z 1 then the series impedance This is a capacitance which is given by

Equivalent circuits Zo Zo. L Zo Zo >> Z 1 Zo Zoc Zo << Z 1 Zo

Transmission line parameters It is interesting that the characteristic impedance and propagation constant of a transmission line can be determined from ABCD matrix as follows

Conversion S to ABCD For conversion of ABCD to S-parameter For conversion of S to ABCD-parameter Zo is a characteristic impedance of the transmission line connected to the ABCD network, usually 50 ohm.

Math. CAD functions for conversion For conversion of ABCD to S-parameter For conversion of S to ABCD-parameter

Odd and Even Mode Analysis Usually use for analyzing a symmetrical four port network (1) Excitation • Equal , in phase excitation – even mode • Equal , out of phase excitation – odd mode (2) Draw intersection line for symmetry and apply • short circuit for odd mode • Open circuit for even mode (3) Also can apply EM analysis of structure • Tangential E field zero – odd mode • Tangential H field zero – even mode (4) Single excitation at one port= even mode + odd mode

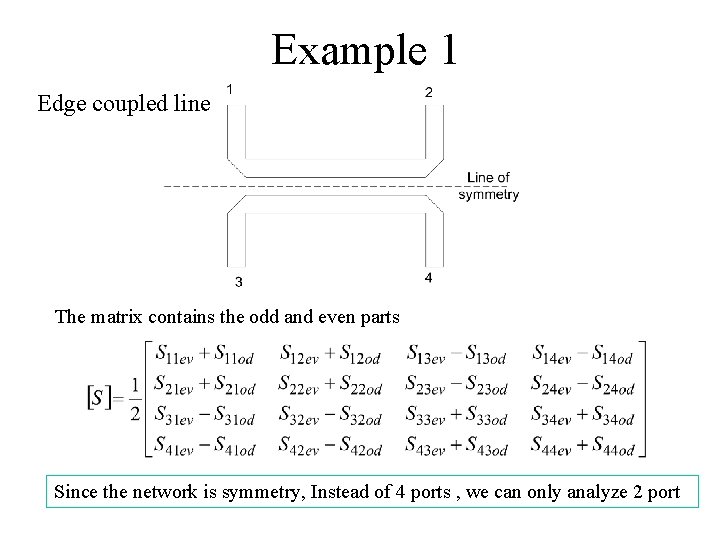
Example 1 Edge coupled line The matrix contains the odd and even parts Since the network is symmetry, Instead of 4 ports , we can only analyze 2 port

continue We just analyze for 2 transmission lines with characteristic Ze and Zo respectively. Similarly the propagation coefficients be and bo respectively. Treat the odd and even mode lines as uniform lossless lines. Taking ABCD matrix for a line , length l, characteristic impedance Z and propagation constant b, thus Using conversion

continue Taking Then (equivalent to quarter-wavelength transmission line)

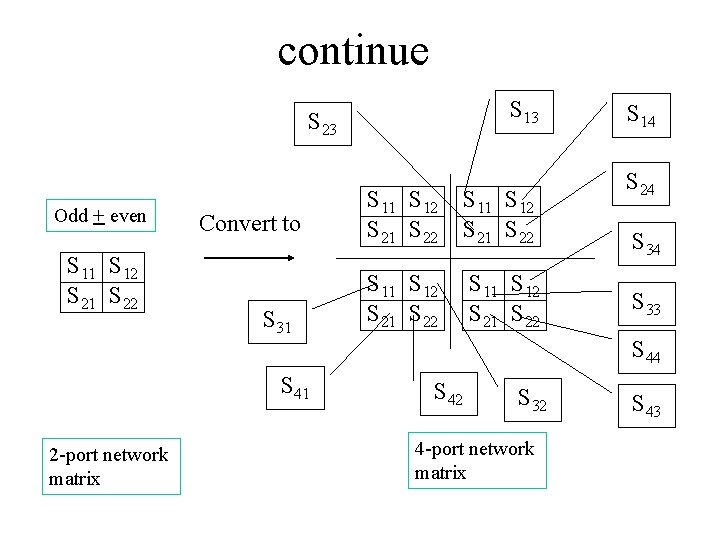
continue S 13 S 23 Odd + even S 11 S 12 S 21 S 22 Convert to S 31 S 41 2 -port network matrix S 11 S 12 S 21 S 22 S 14 S 24 S 33 S 44 S 42 S 32 4 -port network matrix S 43

continue Follow symmetrical properties ev+ od S 11 S 12 S 21 S 22 S 13 S 14 S 23 S 24 ev- od S 31 S 32 S 41 S 42 S 33 S 34 S 43 S 44 Assuming bev = bod = ev- od ev+ od Then For perfect isolation (I. e S 41=S 14=S 32=S 23=0 ), we choose Zev and Zod such that Zev Zod=Zo 2.

continue ev+ od S 11 S 12 S 21 S 22 S 13 S 14 S 23 S 24 ev- od S 31 S 32 S 41 S 42 S 33 S 34 S 43 S 44 ev- od ev+ od Similarly we have Equal to zero if Zev Zod=Zo 2.

continue ev+ od S 11 S 12 S 21 S 22 S 13 S 14 S 23 S 24 ev- od S 31 S 32 S 41 S 42 S 33 S 34 S 43 S 44 ev- od ev+ od We have if Zev Zod=Zo 2.

continue ev+ od S 11 S 12 S 21 S 22 S 13 S 14 S 23 S 24 ev- od S 31 S 32 S 41 S 42 S 33 S 34 S 43 S 44 ev- od ev+ od if Zev Zod=Zo 2.

continue This S-parameter must satisfy network characteristic: (1) Power conservation Reflected power transmitted power to port 2 Since S 11 and S 41=0 , then (2) And quadrature condition transmitted power to port 3 transmitted power to port 4

continue For 3 d. B coupler or Rewrite we have In practice Zev > Zod so However the limitation for coupled edge (Gap size ) also bev and bod are not pure TEM thus not equal

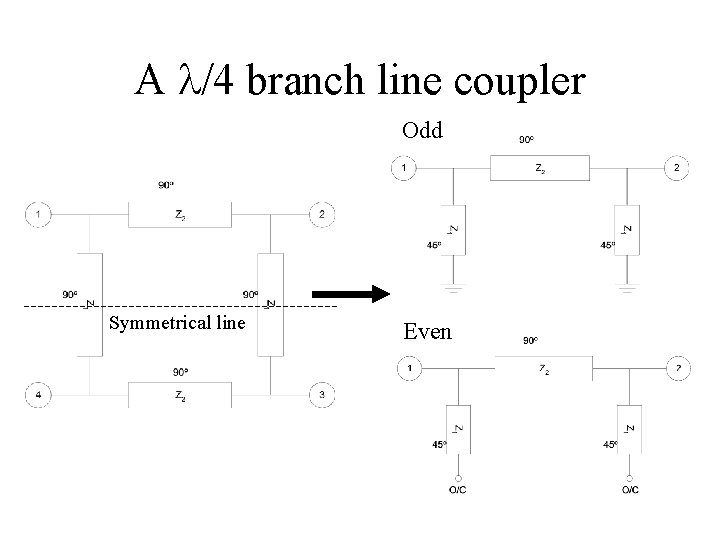
A l/4 branch line coupler Odd Symmetrical line Even

Analysis Stub odd (short circuit) Stub even (open circuit) The ABCD matrices for the two networks may then found : stub Transmission line stub

continue Convert to S For perfect isolation we require Thus or From previous definition

continue Substituting into S-parameter gives us and Therefore for full four port And

continue For power conservation and quadrature conditions to be met Equal split S or And If Zo= 50 W then Z 2 = 35. 4 W