Network Layer Network layer Physical layer move bits

Network Layer

Network layer • Physical layer: move bits between physically connected stations • Data link layer: move frames between physically connected stations • Network layer: move packets from source A to destination B where A and B can be world-apart

Main Network Layer Design Issues • Routing: Where to send the packets received?

Routing • Routing – Determining the path from the source to the destination. At a router, it means which output port should a packet to be sent to • Desirable properties of the routing algorithms: – correctness: of course – simplicity: for efficiency – robustness: must be able to sustain the changes in the networks (cannot just rely on reboot) – stability: when run long enough, should converge to equilibrium – fairness: every one gets to send – optimality: as efficient as possible, of course • sometimes, these properties may conflict

Flooding • Flooding – send all the incoming packet to all outgoing links except the one the packet arrived on – Reliable, fast, large overhead, not scalable – user: military, distributed database(update everything), highly reliable packets.

Flooding • Problems? • A packet will be sent for infinite number of times • Hop count. Don’t forward the same packet for more than H times. – How to set H?

Shortest Path Algorithm • find the shortest path from the source to all other nodes. • Dijkstra algorithm: finding the shortest paths from the source s to all other nodes in the network. 1) Initial set = empty, 2) maintain the distance from s to all other nodes (distance(s, s) = 0, distance(s, t) = infinite) 3) repeat until all nodes are included in the set 4) find a node d currently no in the set with shortest distance 5) include d in the set 6) update the distance from s to all other nodes not in set using 7) if distance(s, m) > distance(s, d) + dist(d, m) then 8) distance(s, m) = distance(s, d) + dist (d, m)
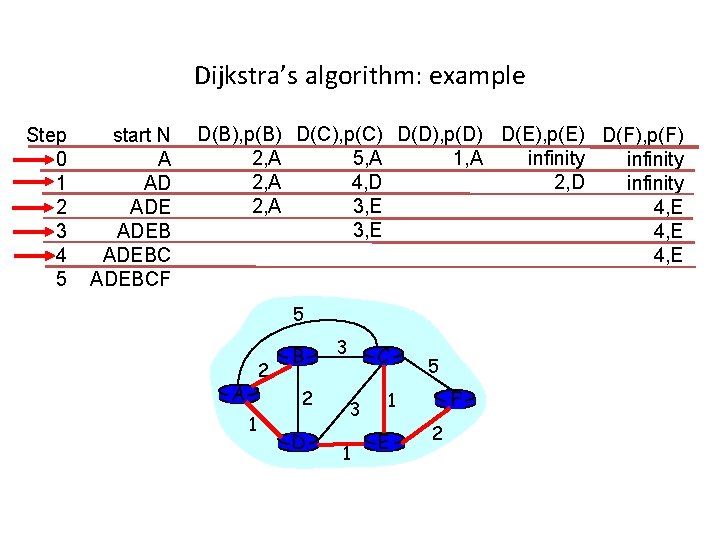
Dijkstra’s algorithm: example Step 0 1 2 3 4 5 start N A AD ADEBCF D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 1, A 5, A infinity 2, A 4, D 2, D infinity 2, A 3, E 4, E 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2

Shortest Path • Node added to the set has found its minimum distance path (visiting ONLY the nodes currently in the set, of course) to the source. – Suppose this is not true. At a step, we add node W to the set. If there is another path s---Z---W with distance shorter than d(W), where Z is the first node in the path currently not in the set. d(Z) must be less than d(W) (why? ) and we would have added Z to the set at this step rather than W. – So if we added W, we are using the shortest path. – Note that any subpath on an optimal path is still optimal.

Link State Algorithm • Each router independently computes optimal paths • Must make sure that • Each router sees the same cost for each link (using the same network topology) • Uses the same algorithm (shortest path algorithm for OSPF) to compute the best path

Distance Vector Algorithm • The LS algorithm works for relatively small networks, because it is necessarily a centralized algorithm. • For larger networks, too expensive to store and disseminate the network topology, use DV algorithms.

Distance Vector Routing Algorithm Distance Table data structure • • • each node has its own row for each possible destination column for each directly-attached neighbor to node example: in node X, for dest. Y via neighbor Z: X D (Y, Z) distance from X to = Y, via Z as next hop Z (Y, w)} = c(X, Z) + min {D w
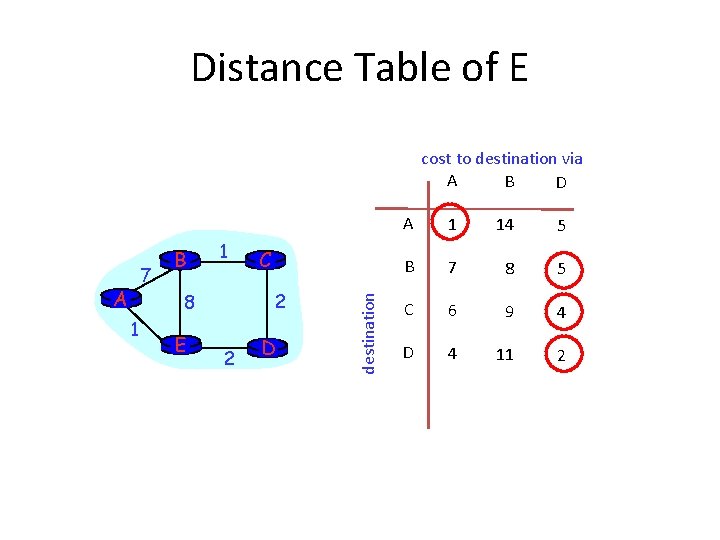
Distance Table of E cost to destination via A B D A 1 2 8 1 E C 2 D destination 7 B A 1 14 5 B 7 8 5 C 6 9 4 D 4 11 2
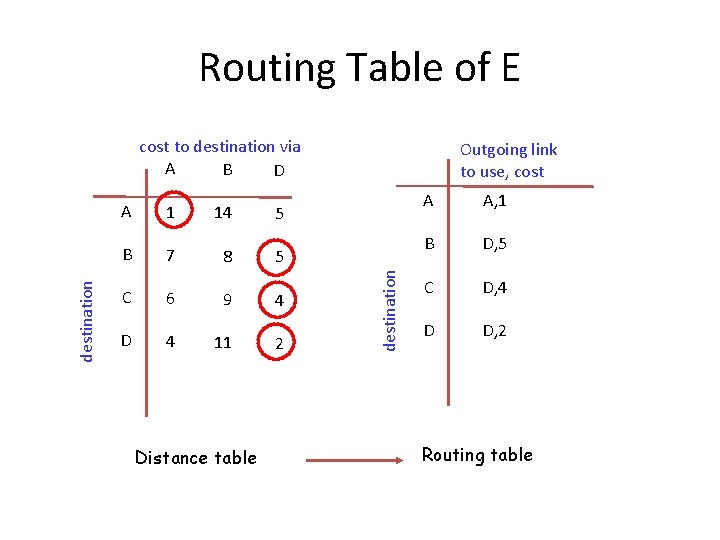
Routing Table of E A 1 14 5 B 7 8 5 C 6 9 4 D 4 11 Distance table 2 Outgoing link to use, cost destination cost to destination via A B D A A, 1 B D, 5 C D, 4 D D, 2 Routing table

Distance Vector Algorithm Iterative, asynchronous: each iteration caused by: • local link cost change • message from neighbor: its least cost path change from neighbor Distributed: • each node notifies neighbors only when its least cost path to any destination changes – neighbors then notify their neighbors if necessary Each node: wait for (change in local link cost or msg from neighbor) recompute distance table if least cost path to any dest has changed, notify neighbors
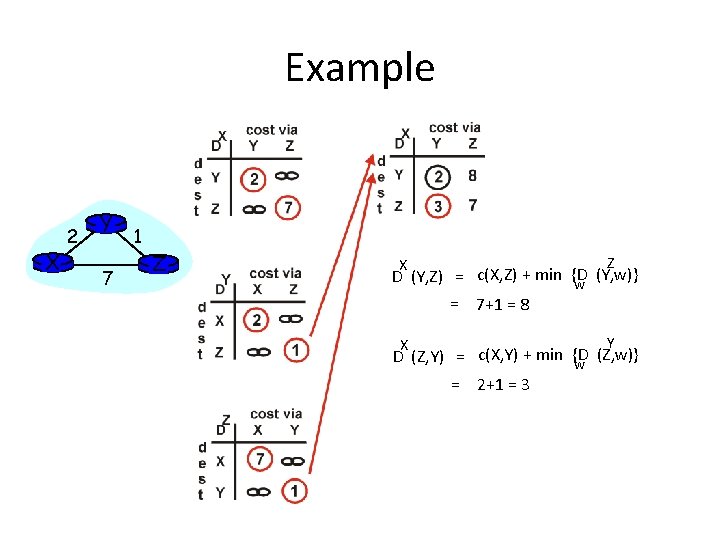
Example X 2 Y 7 1 Z Z X (Y, w)} D (Y, Z) = c(X, Z) + min {D w = 7+1 = 8 Y X (Z, w)} D (Z, Y) = c(X, Y) + min {D w = 2+1 = 3
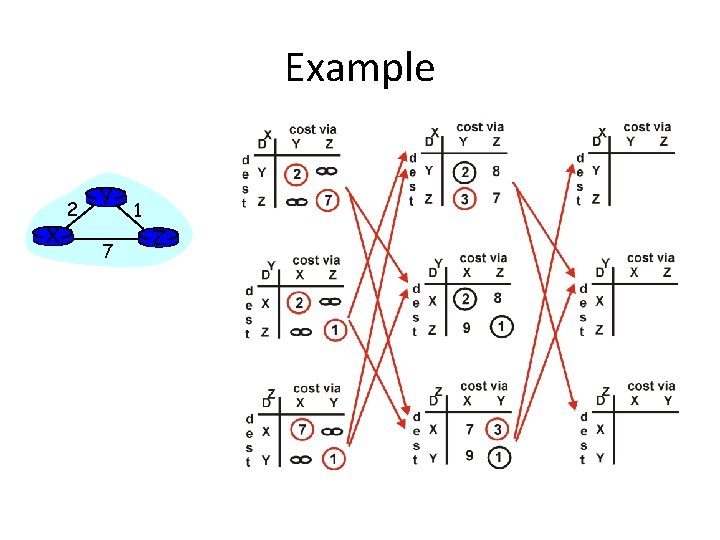
Example X 2 Y 7 1 Z
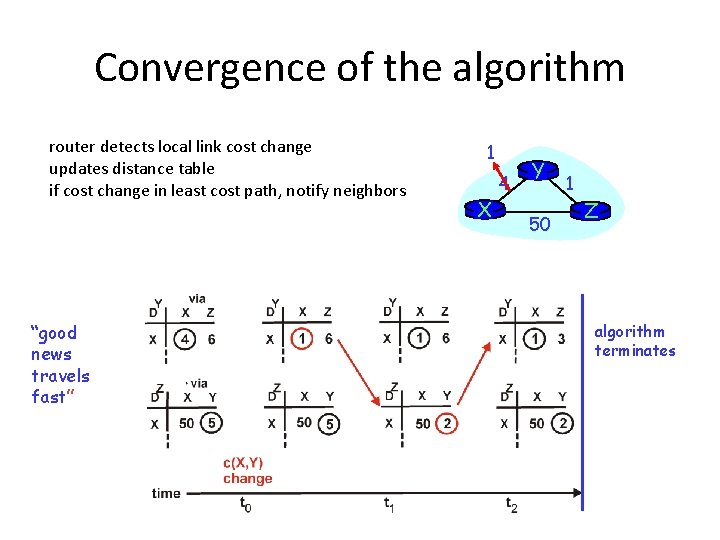
Convergence of the algorithm router detects local link cost change updates distance table if cost change in least cost path, notify neighbors “good news travels fast” 1 X 4 Y 50 1 Z algorithm terminates
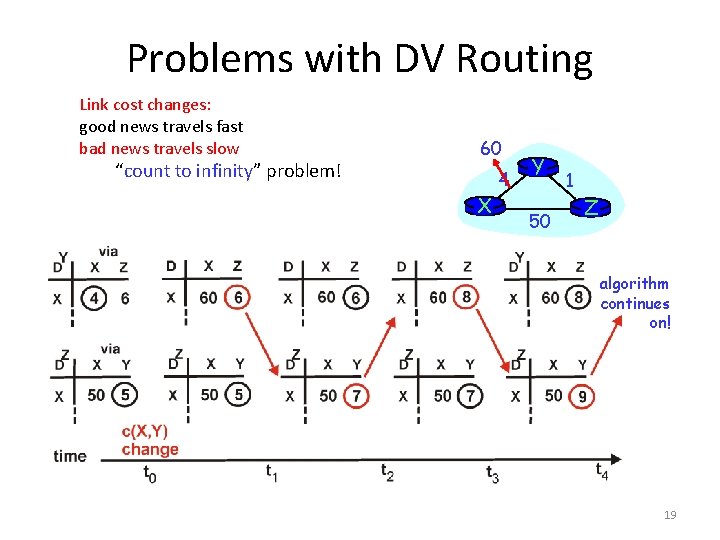
Problems with DV Routing Link cost changes: good news travels fast bad news travels slow “count to infinity” problem! 60 X 4 Y 50 1 Z algorithm continues on! 19
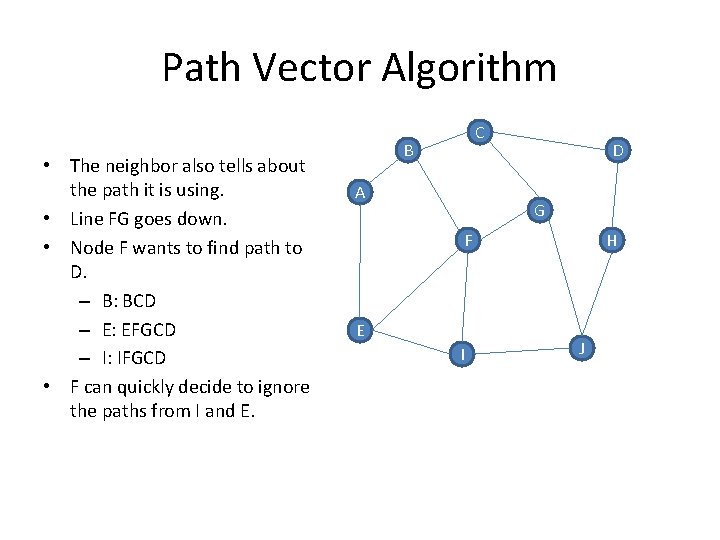
Path Vector Algorithm • The neighbor also tells about the path it is using. • Line FG goes down. • Node F wants to find path to D. – B: BCD – E: EFGCD – I: IFGCD • F can quickly decide to ignore the paths from I and E. C B A D G F E I H J
- Slides: 20