Network Flow Models Chapter 7 Copyright 2010 Pearson

Network Flow Models Chapter 7 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -1

Chapter Topics ■ The Shortest Route Problem ■ The Minimal Spanning Tree Problem ■ The Maximal Flow Problem Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -2

Network Components ■ A network is an arrangement of paths (branches) connected at various points (nodes) through which one or more items move from one point to another. ■ The network is drawn as a diagram providing a picture of the system thus enabling visual representation and enhanced understanding. ■ A large number of real-life systems can be modeled as networks which are relatively easy to conceive and construct. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -3

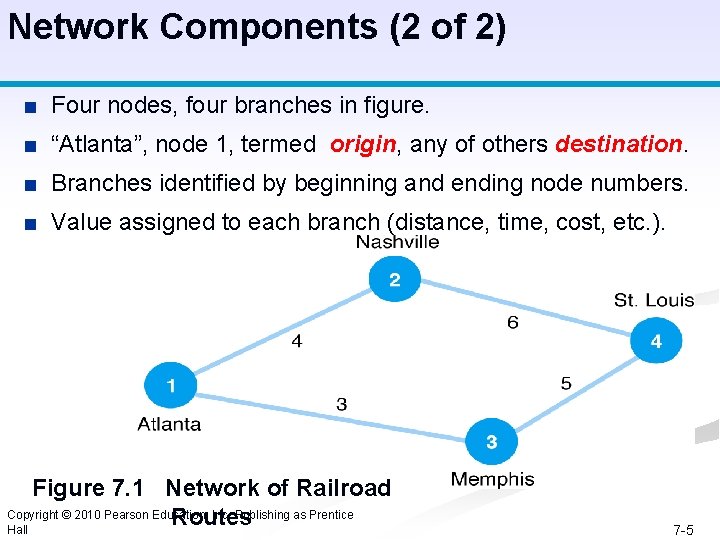
Network Components (1 of 2) ■ Network diagrams consist of nodes and branches. ■ Nodes (circles), represent junction points, or locations. ■ Branches (lines), connect nodes and represent flow. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -4

Network Components (2 of 2) ■ Four nodes, four branches in figure. ■ “Atlanta”, node 1, termed origin, any of others destination. ■ Branches identified by beginning and ending node numbers. ■ Value assigned to each branch (distance, time, cost, etc. ). Figure 7. 1 Network of Railroad Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Routes Hall 7 -5

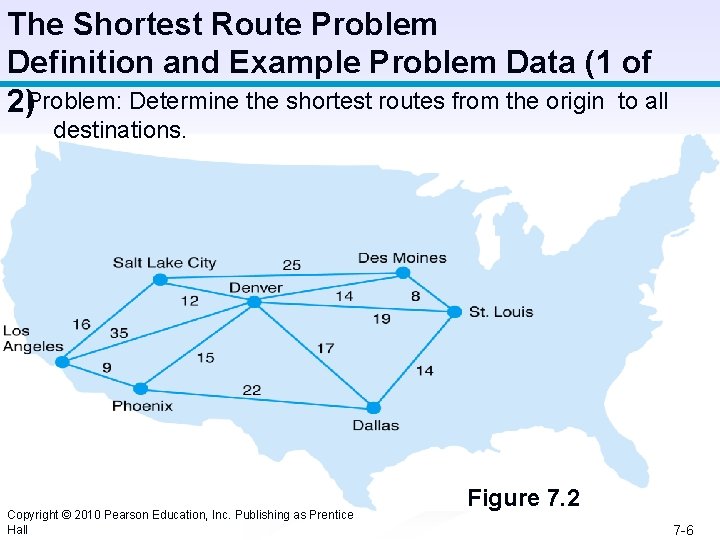
The Shortest Route Problem Definition and Example Problem Data (1 of 2)Problem: Determine the shortest routes from the origin to all destinations. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Figure 7. 2 7 -6

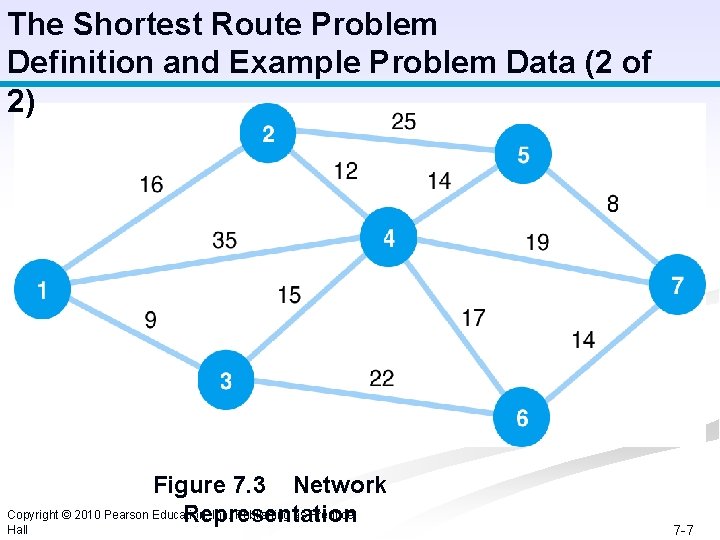
The Shortest Route Problem Definition and Example Problem Data (2 of 2) Figure 7. 3 Network Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Representation Hall 7 -7

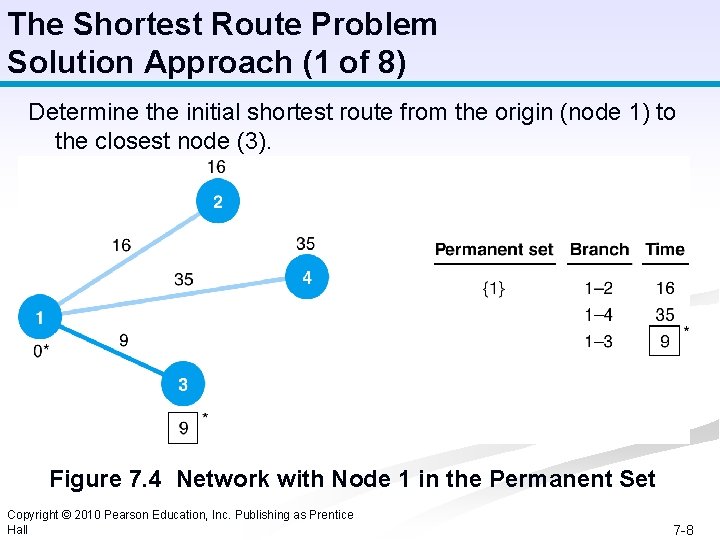
The Shortest Route Problem Solution Approach (1 of 8) Determine the initial shortest route from the origin (node 1) to the closest node (3). Figure 7. 4 Network with Node 1 in the Permanent Set Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -8

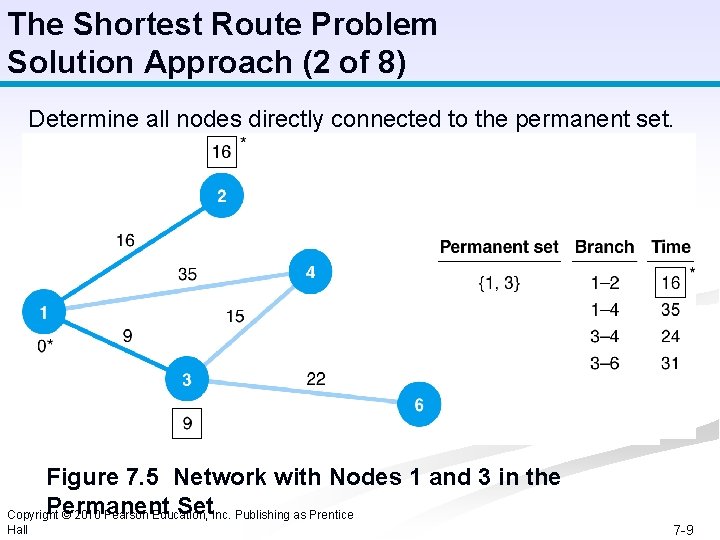
The Shortest Route Problem Solution Approach (2 of 8) Determine all nodes directly connected to the permanent set. Figure 7. 5 Network with Nodes 1 and 3 in the Permanent Set. Inc. Publishing as Prentice Copyright © 2010 Pearson Education, Hall 7 -9

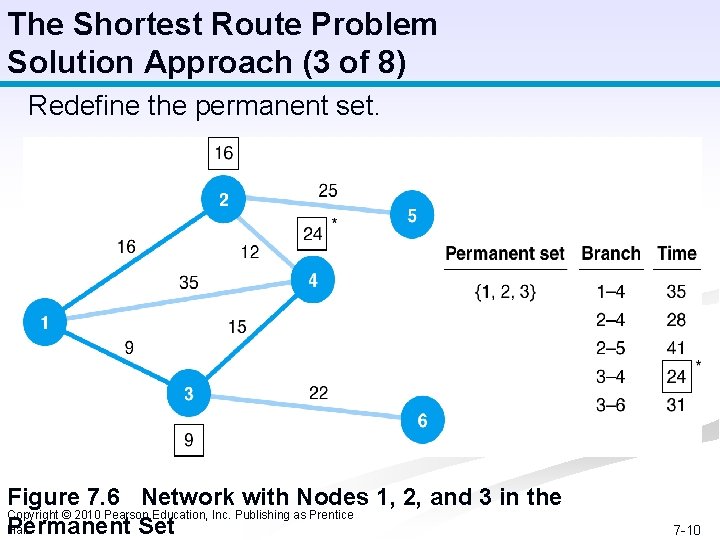
The Shortest Route Problem Solution Approach (3 of 8) Redefine the permanent set. Figure 7. 6 Network with Nodes 1, 2, and 3 in the Permanent Set Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -10

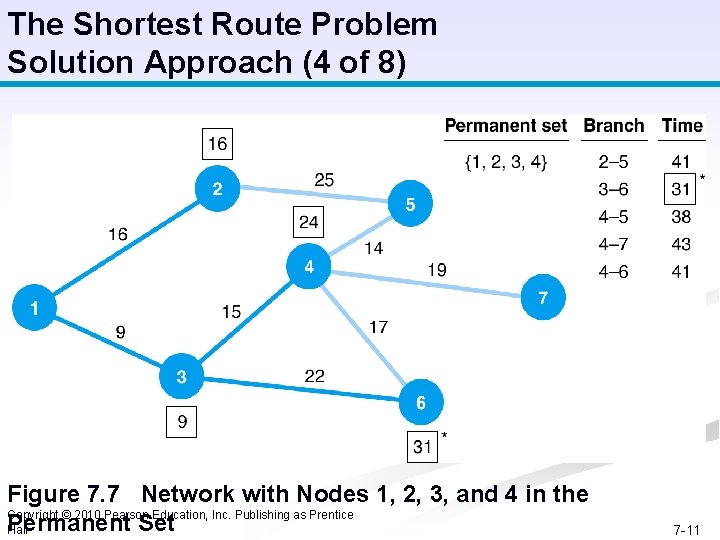
The Shortest Route Problem Solution Approach (4 of 8) Figure 7. 7 Network with Nodes 1, 2, 3, and 4 in the Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Permanent Set Hall 7 -11

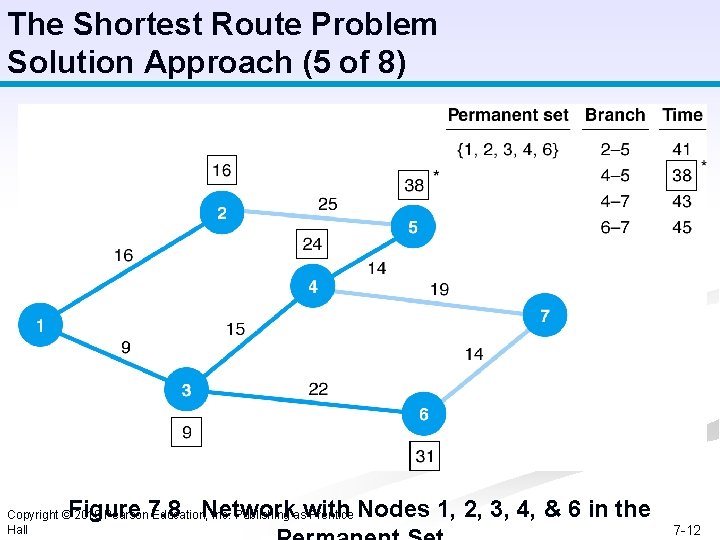
The Shortest Route Problem Solution Approach (5 of 8) Figure 7. 8 Network with Nodes 1, 2, 3, 4, & 6 in the Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -12

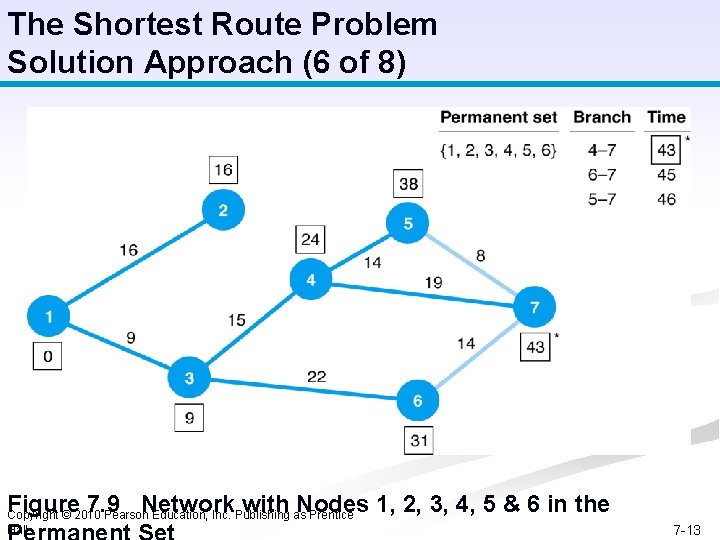
The Shortest Route Problem Solution Approach (6 of 8) Figure 7. 9 Network with Nodes 1, 2, 3, 4, 5 & 6 in the Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -13

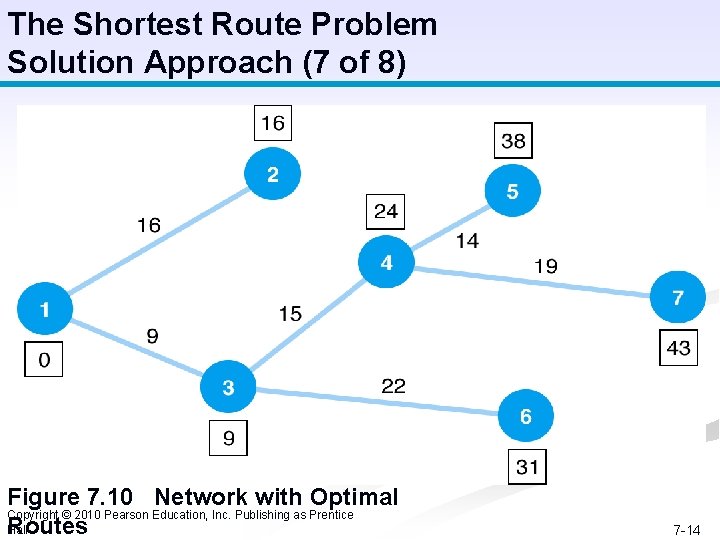
The Shortest Route Problem Solution Approach (7 of 8) Figure 7. 10 Network with Optimal Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Routes 7 -14

The Shortest Route Problem Solution Approach (8 of 8) Table 7. 1 Shortest Travel Time from Origin to Each Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Destination Hall 7 -15

The Shortest Route Problem Solution Method Summary 1. Select the node with the shortest direct route from the origin. 2. Establish a permanent set with the origin node and the node that was selected in step 1. 3. Determine all nodes directly connected to the permanent set of nodes. 4. Select the node with the shortest route from the group of nodes directly connected to the permanent set of nodes. 5. Repeat steps 3 & 4 until all nodes have joined the set. Copyrightpermanent © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -16

The Shortest Route Problem Computer Solution with QM for Windows (1 of 2) Exhibit 7. 1 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -17

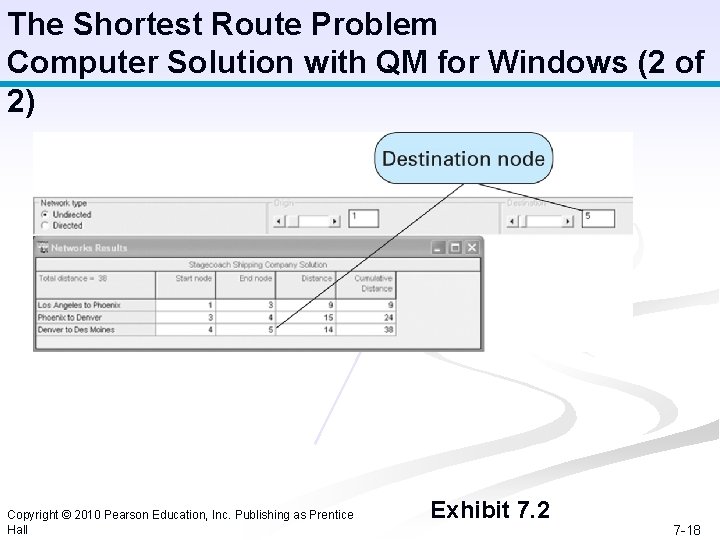
The Shortest Route Problem Computer Solution with QM for Windows (2 of 2) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 7. 2 7 -18

The Shortest Route Problem Computer Solution with Excel (1 of 4) Formulation as a 0 - 1 integer linear programming problem. xij = 0 if branch i-j is not selected as part of the shortest route and 1 if it is selected. Minimize Z = 16 x 12 + 9 x 13 + 35 x 14 + 12 x 24 + 25 x 25 + 15 x 34 + 22 x 36 + 14 x 45 + 17 x 46 + 19 x 47 + 8 x 57 + 14 x 67 subject to: x 12 + x 13 + x 14= 1 x 12 - x 24 - x 25 = 0 x 13 - x 34 - x 36 = 0 x 14 + x 24 + x 34 - x 45 - x 46 - x 47 = 0 x 25 + x 45 - x 57 = 0 x 36 + x 46 - x 67 = 0 x 47 + x 57 + x 67 = 1 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall xij = 0 or 1 7 -19

The Shortest Route Problem Computer Solution with Excel (2 of 4) Exhibit 7. 3 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -20

The Shortest Route Problem Computer Solution with Excel (3 of 4) Exhibit 7. 4 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -21

The Shortest Route Problem Computer Solution with Excel (4 of 4) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 7. 5 7 -22

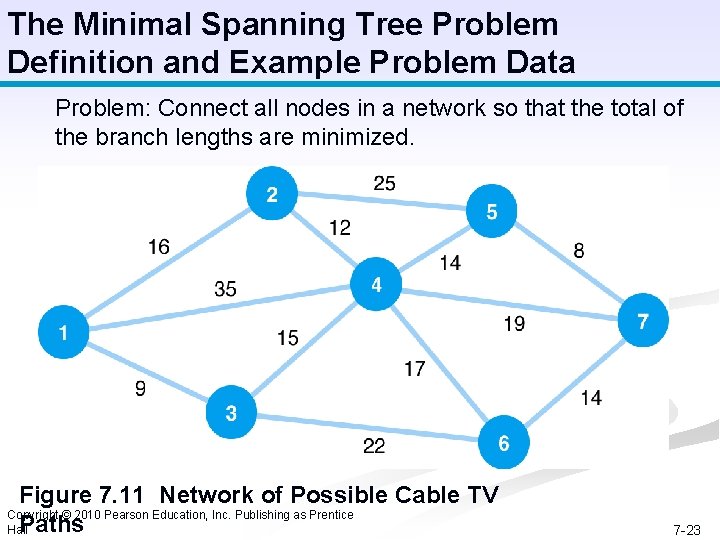
The Minimal Spanning Tree Problem Definition and Example Problem Data Problem: Connect all nodes in a network so that the total of the branch lengths are minimized. Figure 7. 11 Network of Possible Cable TV Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Paths Hall 7 -23

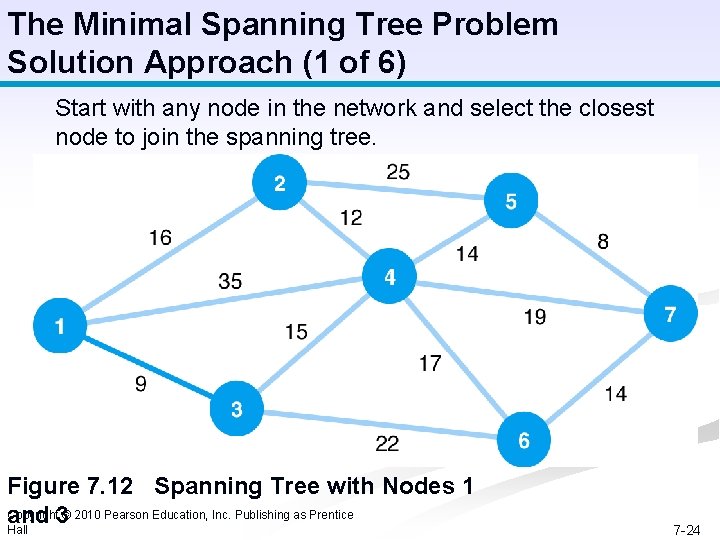
The Minimal Spanning Tree Problem Solution Approach (1 of 6) Start with any node in the network and select the closest node to join the spanning tree. Figure 7. 12 Spanning Tree with Nodes 1 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice and 3 Hall 7 -24

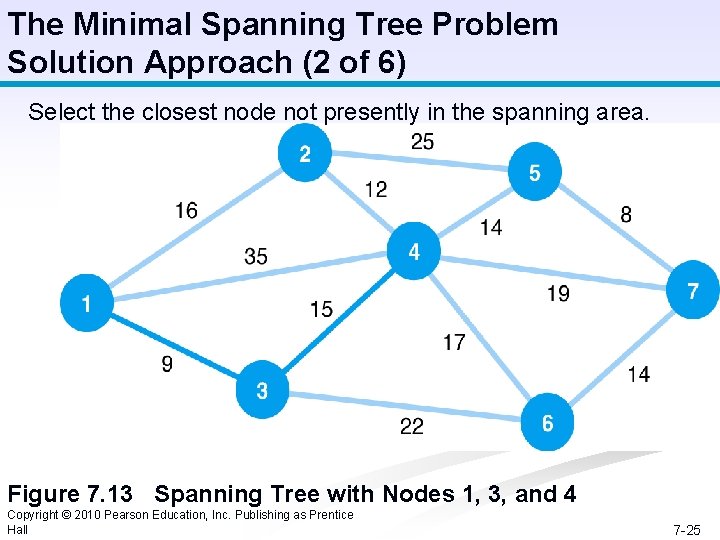
The Minimal Spanning Tree Problem Solution Approach (2 of 6) Select the closest node not presently in the spanning area. Figure 7. 13 Spanning Tree with Nodes 1, 3, and 4 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -25

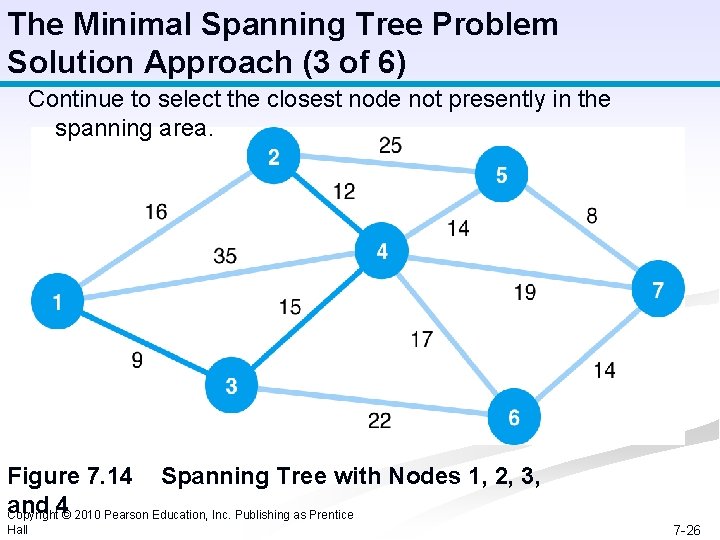
The Minimal Spanning Tree Problem Solution Approach (3 of 6) Continue to select the closest node not presently in the spanning area. Figure 7. 14 Spanning Tree with Nodes 1, 2, 3, and 4 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -26

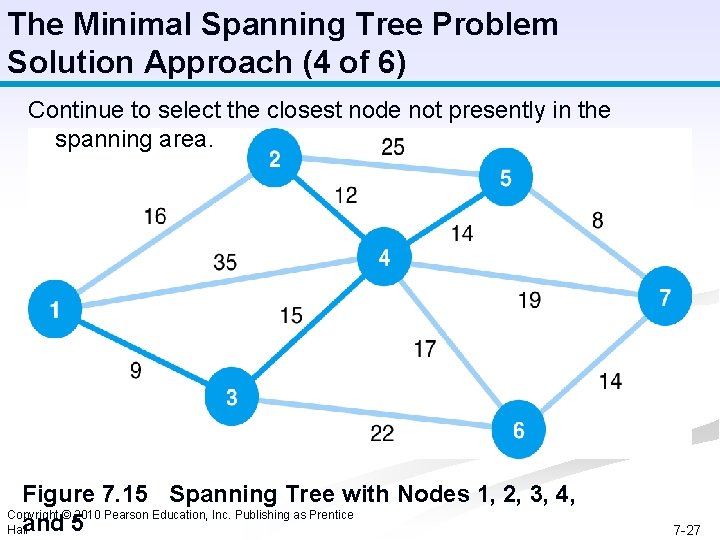
The Minimal Spanning Tree Problem Solution Approach (4 of 6) Continue to select the closest node not presently in the spanning area. Figure 7. 15 Spanning Tree with Nodes 1, 2, 3, 4, Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Halland 5 7 -27

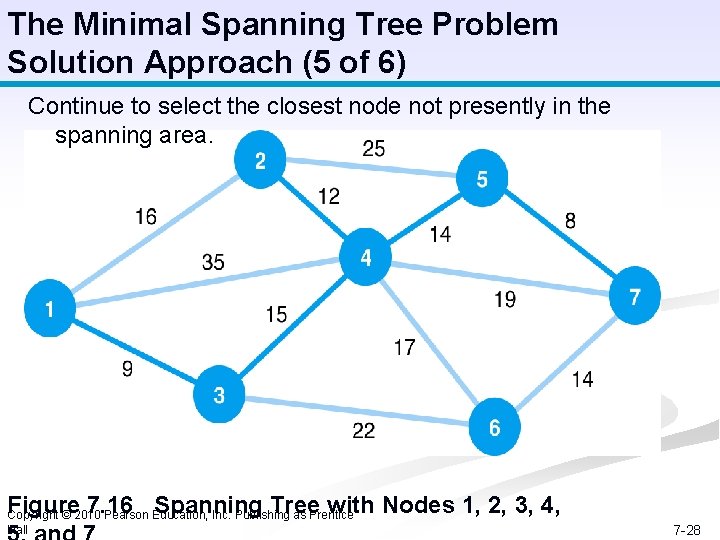
The Minimal Spanning Tree Problem Solution Approach (5 of 6) Continue to select the closest node not presently in the spanning area. Figure 7. 16 Spanning Tree with Nodes 1, 2, 3, 4, Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -28

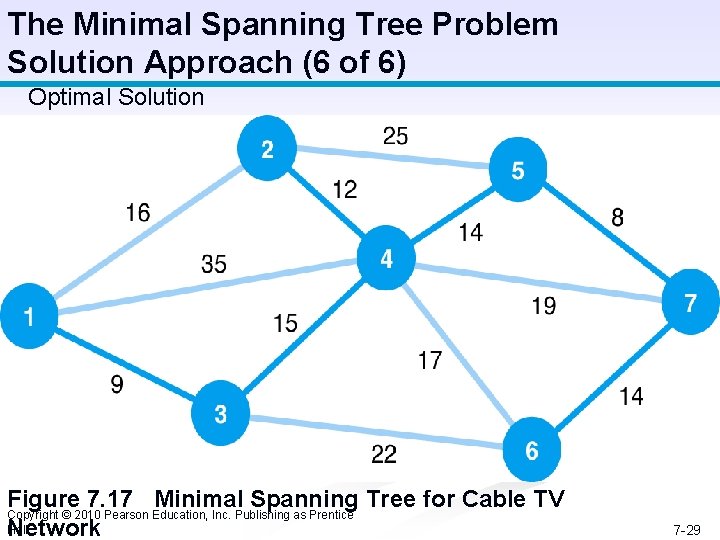
The Minimal Spanning Tree Problem Solution Approach (6 of 6) Optimal Solution Figure 7. 17 Minimal Spanning Tree for Cable TV Network Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -29

The Minimal Spanning Tree Problem Solution Method Summary 1. Select any starting node (conventionally, node 1). 2. Select the node closest to the starting node to join the spanning tree. 3. Select the closest node not presently in the spanning tree. 4. Repeat step 3 until all nodes have joined the spanning tree. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -30

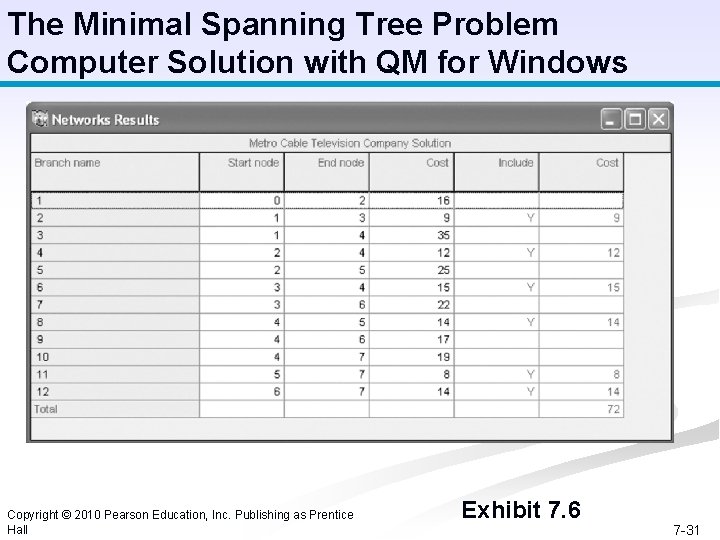
The Minimal Spanning Tree Problem Computer Solution with QM for Windows Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 7. 6 7 -31

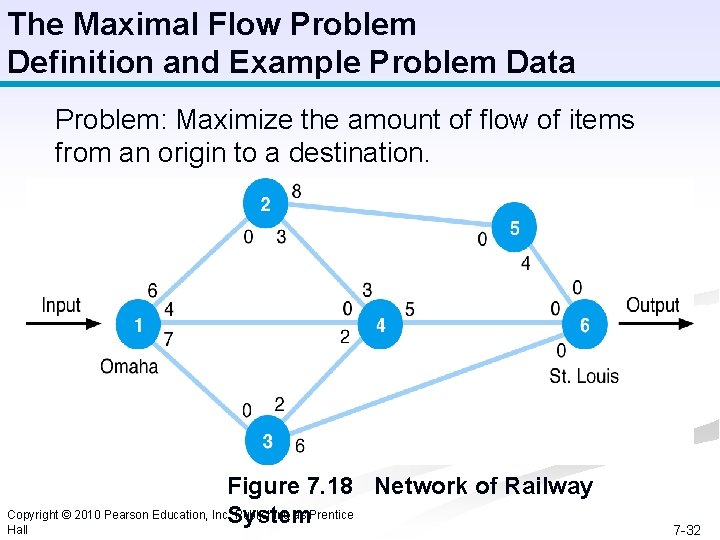
The Maximal Flow Problem Definition and Example Problem Data Problem: Maximize the amount of flow of items from an origin to a destination. Figure 7. 18 Network of Railway Copyright © 2010 Pearson Education, Inc. System Publishing as Prentice Hall 7 -32

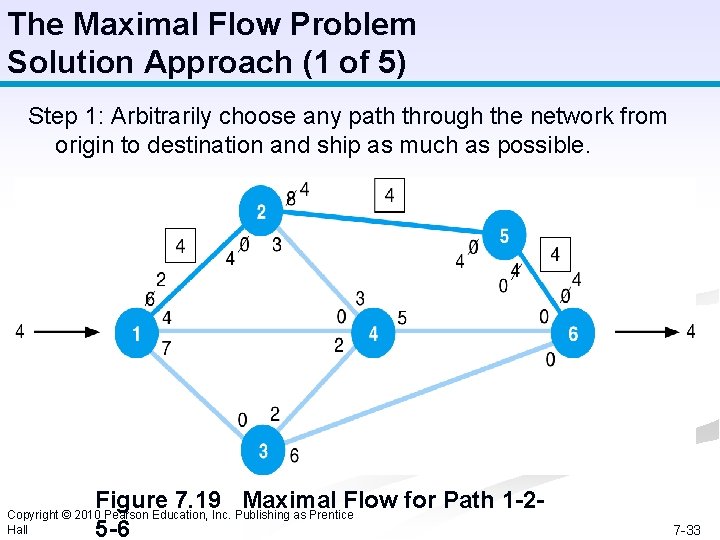
The Maximal Flow Problem Solution Approach (1 of 5) Step 1: Arbitrarily choose any path through the network from origin to destination and ship as much as possible. Figure 7. 19 Maximal Flow for Path 1 -25 -6 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -33

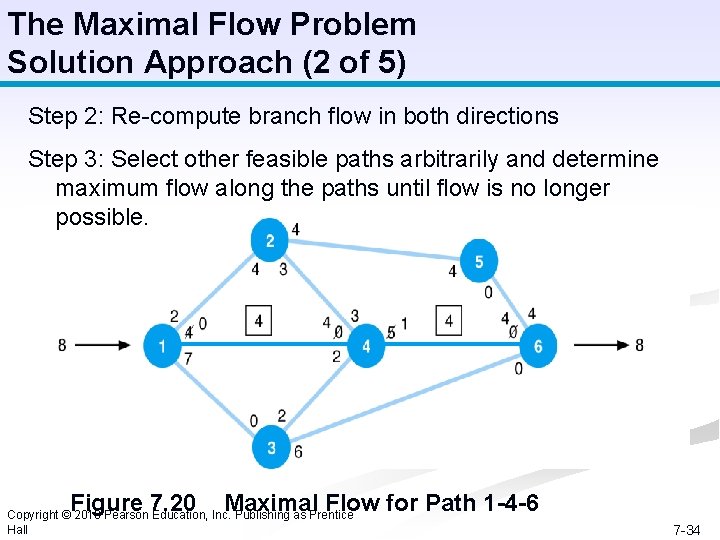
The Maximal Flow Problem Solution Approach (2 of 5) Step 2: Re-compute branch flow in both directions Step 3: Select other feasible paths arbitrarily and determine maximum flow along the paths until flow is no longer possible. Figure 7. 20 Maximal Flow for Path 1 -4 -6 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -34

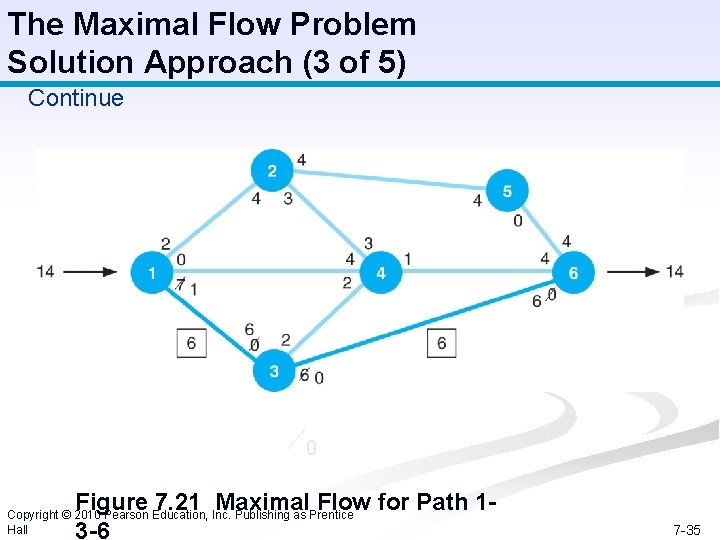
The Maximal Flow Problem Solution Approach (3 of 5) Continue 0 Figure 7. 21 Maximal Flow for Path 13 -6 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -35

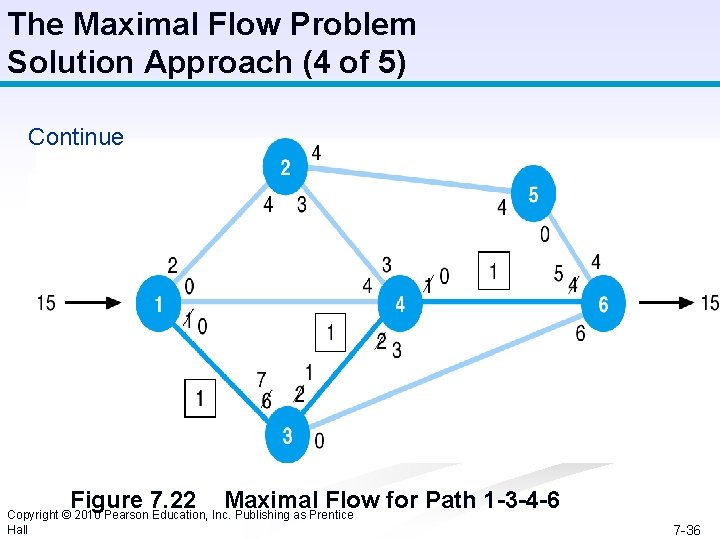
The Maximal Flow Problem Solution Approach (4 of 5) Continue Figure 7. 22 Maximal Flow for Path 1 -3 -4 -6 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -36

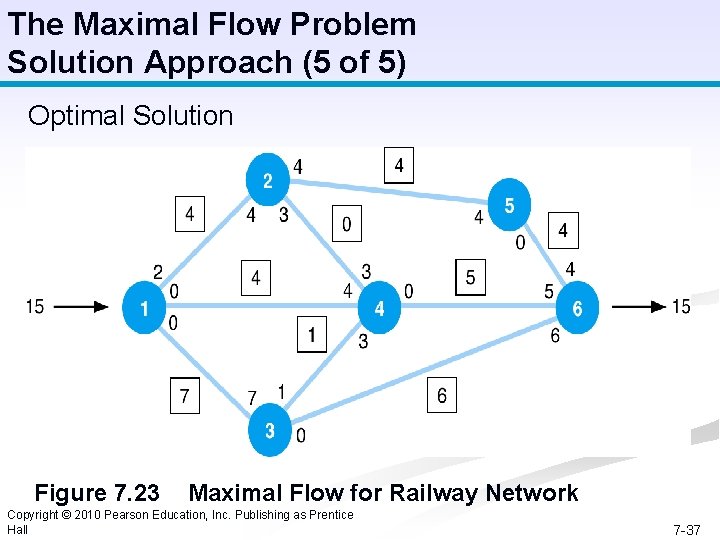
The Maximal Flow Problem Solution Approach (5 of 5) Optimal Solution Figure 7. 23 Maximal Flow for Railway Network Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -37

The Maximal Flow Problem Solution Method Summary 1. Arbitrarily select any path in the network from origin to destination. 2. Adjust the capacities at each node by subtracting the maximal flow for the path selected in step 1. 3. Add the maximal flow along the path to the flow in the opposite direction at each node. 4. Repeat steps 1, 2, and 3 until there are no more paths with available flow capacity. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -38

The Maximal Flow Problem Computer Solution with QM for Windows Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 7. 7 7 -39

The Maximal Flow Problem Computer Solution with Excel (1 of 4) xij = flow along branch i-j and integer Maximize Z = x 61 subject to: x 61 - x 12 - x 13 - x 14 = 0 x 12 - x 24 - x 25 = 0 x 13 - x 34 - x 36 = 0 x 14 + x 24 + x 34 - x 46 = 0 x 25 - x 56 = 0 x 36 + x 46 + x 56 - x 61 = 0 x 12 6 x 24 3 x 34 2 x 13 7 x 25 8 x 36 6 x 14 4 x 46 5 x 56 4 x 61 17 xij 0 and integer Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -40

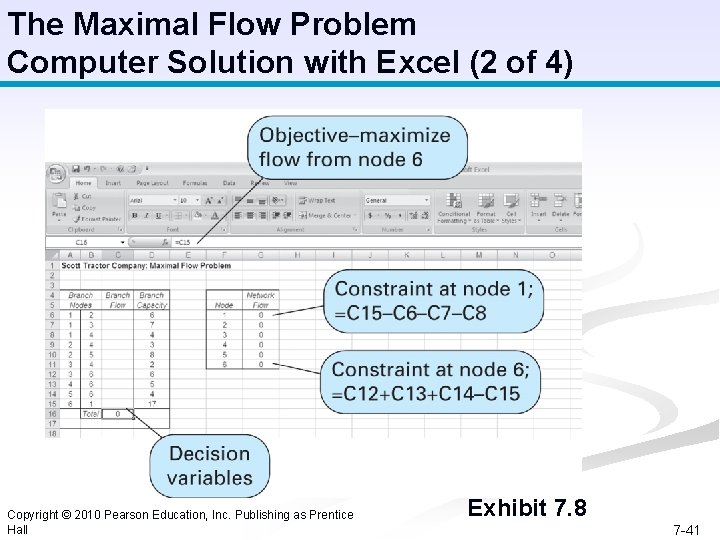
The Maximal Flow Problem Computer Solution with Excel (2 of 4) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 7. 8 7 -41

The Maximal Flow Problem Computer Solution with Excel (3 of 4) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 7. 9 7 -42

The Maximal Flow Problem Computer Solution with Excel (4 of 4) Exhibit 7. 10 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -43

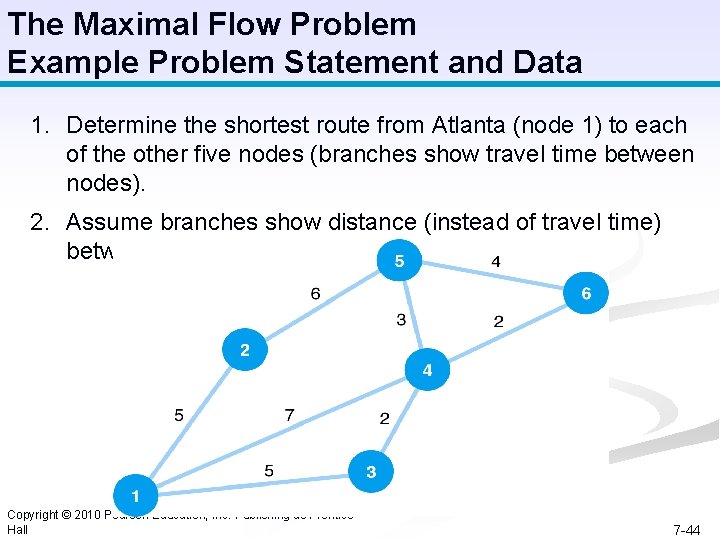
The Maximal Flow Problem Example Problem Statement and Data 1. Determine the shortest route from Atlanta (node 1) to each of the other five nodes (branches show travel time between nodes). 2. Assume branches show distance (instead of travel time) between nodes, develop a minimal spanning tree. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -44

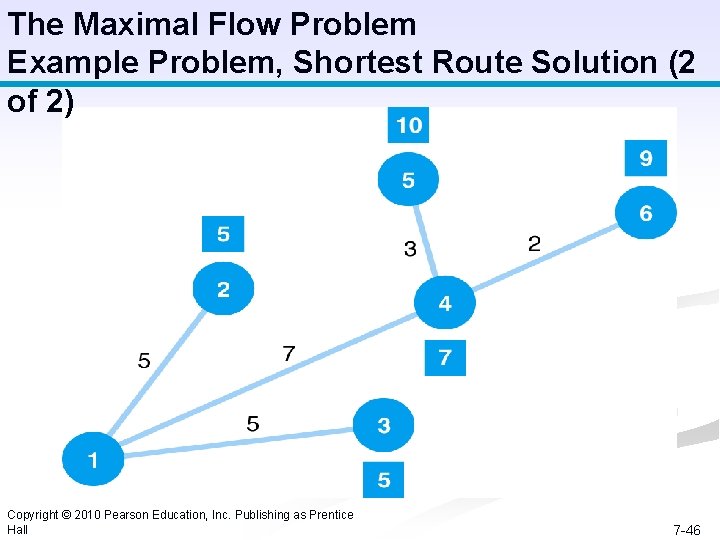
The Maximal Flow Problem Example Problem, Shortest Route Solution (1 of. Step 2) 1 (part A): Determine the Shortest Route Solution 1. Permanent Set {1} 2. {1, 2} 3. {1, 2, 3} 4. {1, 2, 3, 4} 5. {1, 2, 3, 4, 6} 6. {1, 2, 3, 4, 5, 6} Branch 1 -2 1 -3 1 -4 2 -5 3 -4 4 -5 4 -6 4 -5 6 -5 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Time [5] 5 7 [5] 7 11 [7] 11 7 10 [9] [10] 13 7 -45

The Maximal Flow Problem Example Problem, Shortest Route Solution (2 of 2) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -46

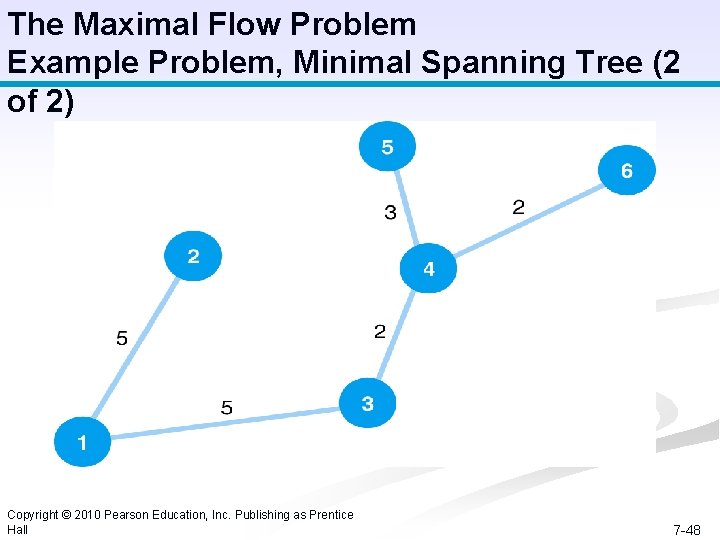
The Maximal Flow Problem Example Problem, Minimal Spanning Tree (1 of 2) 1. The closest unconnected node to node 1 is node 2. 2. The closest to 1 and 2 is node 3. 3. The closest to 1, 2, and 3 is node 4. 4. The closest to 1, 2, 3, and 4 is node 6. 5. The closest to 1, 2, 3, 4 and 6 is 5. 6. The shortest total distance is 17 miles. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -47

The Maximal Flow Problem Example Problem, Minimal Spanning Tree (2 of 2) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -48

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 7 -49