Network Flow CS 494594 Graph Theory Alexander Sayers

Network Flow CS 494/594 – Graph Theory Alexander Sayers

Contents § § § § Definitions History Examples/Algorithms Applications Open Problems References Homework

Definitions §

Maximum Flow § Image from West

Min Cut § Image from West

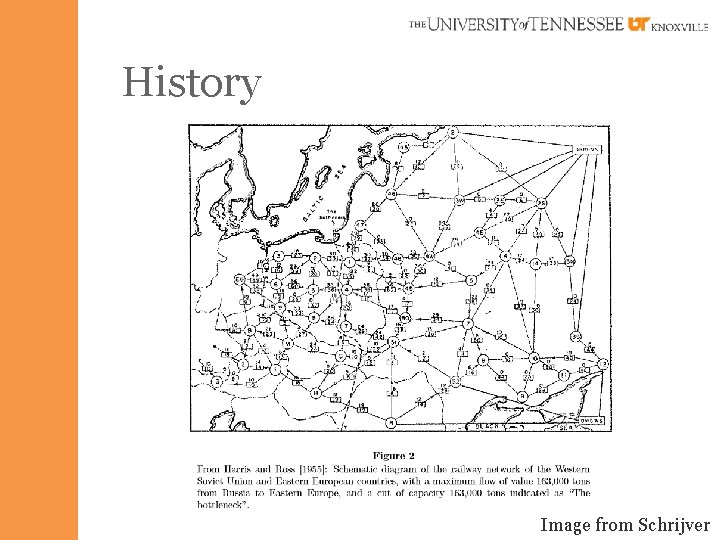
History § A. N. Tolstoi (1930) – “Methods of finding the minimal total kilometrage in cargo-transportation planning in space. ” – Soviet rail networks – Optimum solution does not have any negative-cost cycle in its residual graph.

History Image from Schrijver

History § T. E. Harris and General F. S. Ross (1955) – “Fundamentals of a Method for Evaluating Rail Net Capacities” – Formulated the network flow problem. – “Consider a rail network connecting two cities by way of a number of intermediate cities, where each link of the network has a number assigned to it representing its capacity. Assuming a steady state condition, find a maximal flow from one given city to the other. ”

History § L. R. Ford and D. R. Fulkerson (1956) – “Maximal Flow through a Network” – Proposed the Ford-Fulkerson Algorithm that works in the “cases of most practical interest” by taking advantage of the network planarity.

Ford-Fulkerson Algorithm § Algorithm – Begin with edges initialized to a flow of 0. – While there is a path (no specific path choosing method) from source to sink with capacity remaining. • Increase the flow on each edge, by the amount equal to the minimum of the residual capacities of the edges on the path. • Establish edges in the reverse direction of equal flow. – Continue until there is no such path remaining. – The flow into the sink is the maximum flow.

Failures of FF Algorithm § Pathological scenarios Image from Wiki § Failure to halt – Ford and Fulkerson gave as an example a network with 10 vertices and 48 edges on which their algorithm may fail to halt. – Zwick proved that the smallest possible example of failing to halt is a network that has only 6 vertices and 8 edges.

Failures of FF Algorithm §

Failures of FF Algorithm Residual Values Step Augment. path Sent Flow e 1 e 2 0 1 1 1 0 2 0 3 4 5 e 3 0 0 0 Image from Wiki

History § E. A. Dinitz (1970) – “Algorithm for solution of a problem of maximum flow in a network with power estimation. ” – First publication of the Edmonds-Karp Algorithm. – Created Dinitz’s Algorithm. Image from http: //www. cs. bgu. ac. il/~dinitz/

History § J. Edmonds and R. M. Karp (1972) – “Theoretical improvements in algorithmic efficiency for network flow problems. ” – Independently published the Edmonds-Karp Algorithm. Image from http: //www. iasi. cnr. it/jack/ Image from UC Berkley

Edmonds-Karp/Dinitz’s Alg. §

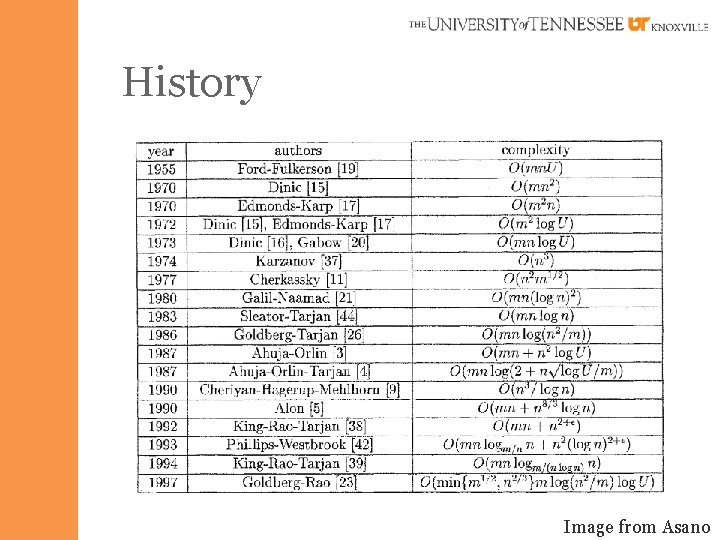
History § R. K. Ahuja, T. L. Magnanti and J. B. Orlin (1993) – “Network Flow: Theory, Algorithms, and Applications. ” – Developed a faster algorithm (a strongly polynomial running time algorithm) to solve network problems.

History Image from Asano

Applications § § § § Edge Disjoint Paths Bipartite Matching Baseball Elimination Problem Project Selection Image Segmentation Open Pit Mining Survey Design And many more (Ahuja, Magnanti, Orlin and Reddy came up with a very complete list of applications).

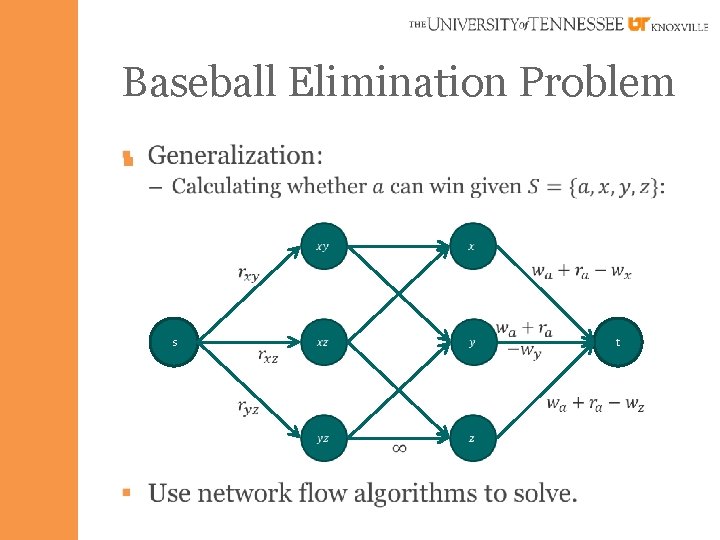
Baseball Elimination Problem § Goal: – Calculate which teams can still win given all possible outcomes of remaining games. – Winning involves having won the most (or equal most) games at the conclusion of all games.

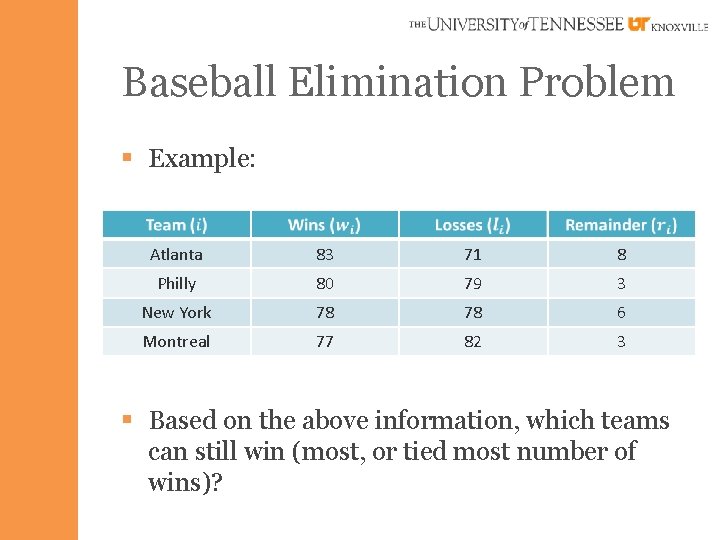
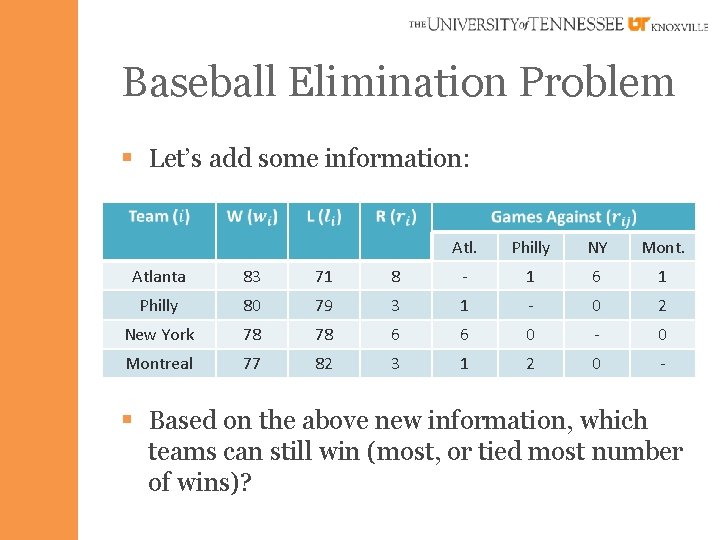
Baseball Elimination Problem § Example: Atlanta 83 71 8 Philly 80 79 3 New York 78 78 6 Montreal 77 82 3 § Based on the above information, which teams can still win (most, or tied most number of wins)?

Baseball Elimination Problem § Let’s add some information: Atl. Philly NY Mont. Atlanta 83 71 8 - 1 6 1 Philly 80 79 3 1 - 0 2 New York 78 78 6 6 0 - 0 Montreal 77 82 3 1 2 0 - § Based on the above new information, which teams can still win (most, or tied most number of wins)?

Baseball Elimination Problem §

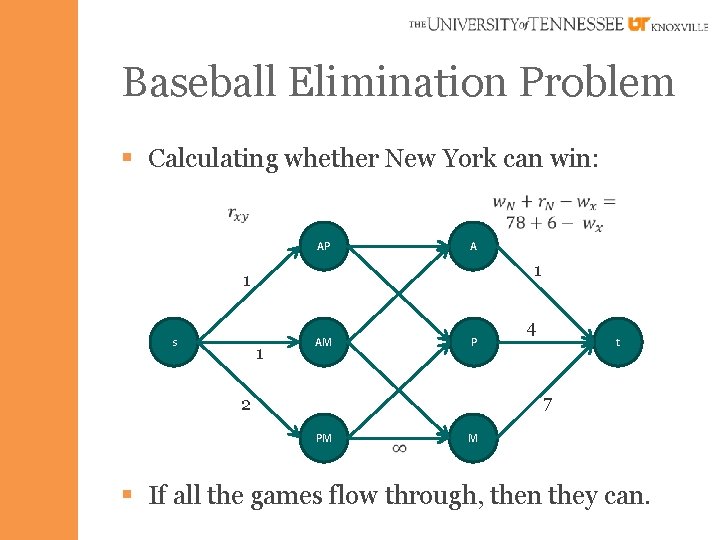
Baseball Elimination Problem § Calculating whether New York can win: AP A 1 1 s 1 AM P 4 t 7 2 PM M § If all the games flow through, then they can.

Baseball Elimination Problem § s t

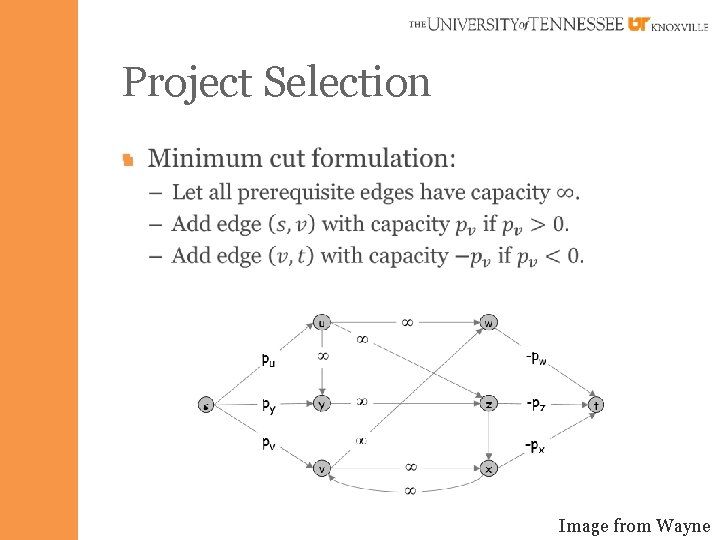
Project Selection § Goal: – Choose a feasible subset of projects to maximize revenue.

Project Selection §

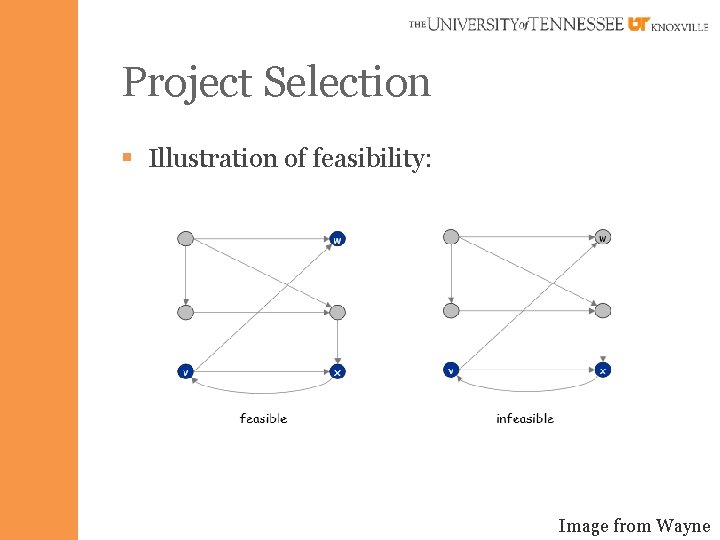
Project Selection § Illustration of feasibility: Image from Wayne

Project Selection § Image from Wayne

Project Selection § Image from Wayne

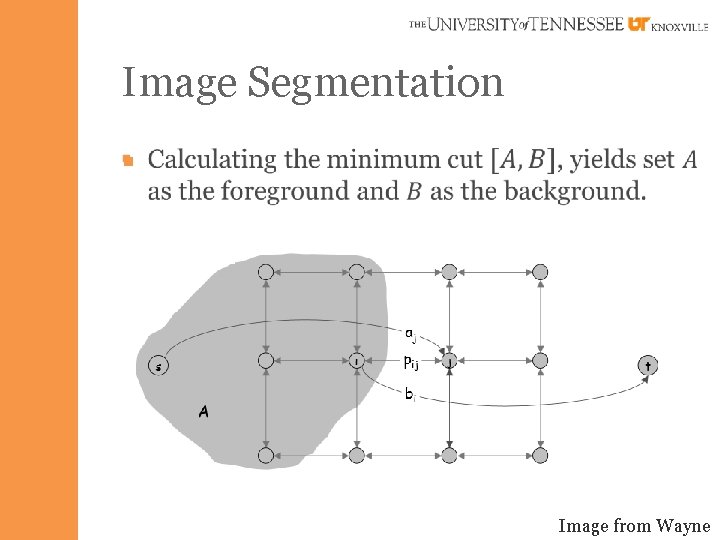
Image Segmentation § Goal: – Identify foreground and background in a complex scene.

Image Segmentation §

Image Segmentation § Objective is to maximize the following: § Turn this into a minimization problem: Image from Wayne

Image Segmentation § Image from Wayne

Open Problems §

References § § § § § Ahuja, R. K. ; Magnanti, T. L. ; Orlin, J. B. (1993). “Network flow: theory, algorithms, and applications”. Prentice Hall. Ahuja, R. K. ; Magnanti, T. L. ; Orlin, J. B. ; Reddy, M. R. (June 1994). “Applications of network optimization”. Asano, T. ; Asano, Y. (2000) “Recent developments in maximum flow algorithms”. Journal of the Operations Research. Society of Japan 43 (2). Biedl, T. C. ; Brejova, B. ; Vinar, T. (2000). “Simplifying flow networks”. Department of Computer Science, University of Waterloo. Dinic, E. A. (1970). "Algorithm for solution of a problem of maximum flow in a network with power estimation". Soviet Math. Doklady (Doklady) 11: 1277– 1280. Edmonds, Jack; Karp, Richard M. (1972). "Theoretical improvements in algorithmic efficiency for network flow problems". Journal of the ACM (Association for Computing Machinery) 19 (2): 248– 264. Ford, L. R. ; Fulkerson, D. R. (1956). "Maximal flow through a network". Canadian Journal of Mathematics 8: 399. Schrijver, Alexander (2002). “On the history of the transportation and maximum flow problems. ” [51] Schrijver, A. West, Douglas B. (2001). “Introduction to Graph Theory (2 nd Edition). ” Pearson Education.

References § Zwick, Uri (21 August 1995). "The smallest networks on which the Ford-Fulkerson maximum flow procedure may fail to terminate". Theoretical Computer Science 148 (1): 165– 170.

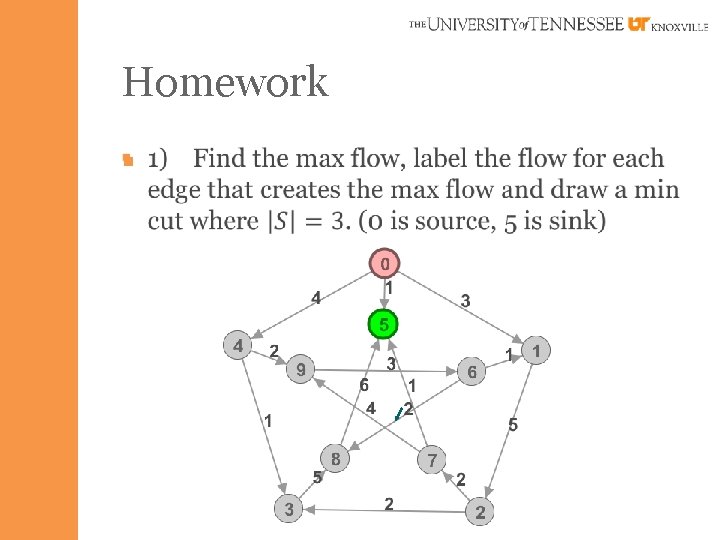
Homework §

Homework § 2) Given a directed graph where the vertices are assigned maximum capacities as well as the edges. Describe/illustrate how you would calculate maximum flow of this graph using established network flow theory/algorithms?

Questions