Network Flow Algorithm 2018 Chungnam National University System

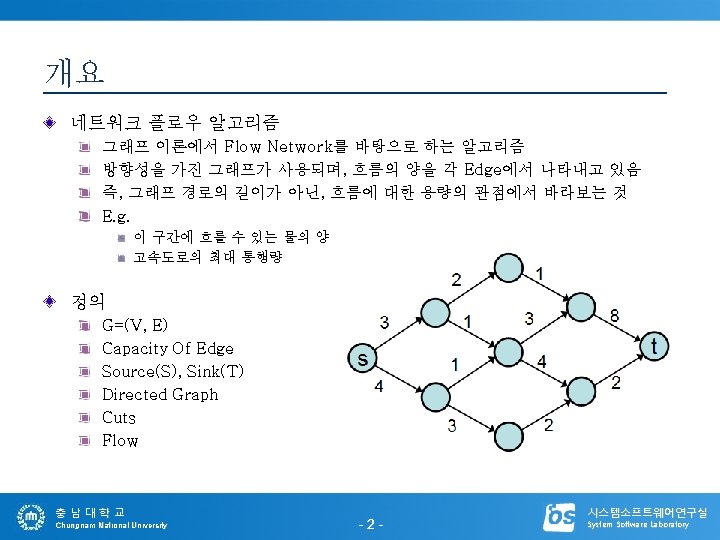


![algorithm Edmonds. Karp input: C[1. . n, 1. . n] (Capacity matrix) T[1. . algorithm Edmonds. Karp input: C[1. . n, 1. . n] (Capacity matrix) T[1. .](https://slidetodoc.com/presentation_image_h2/5f2534f3e701683bd8c0a7d0affea713/image-12.jpg)






- Slides: 22

Network Flow Algorithm 2018. 이상길 충남대학교 Chungnam National University 시스템소프트웨어연구실 System Software Laboratory


충남대학교 Chungnam National University -3 - 시스템소프트웨어연구실 System Software Laboratory


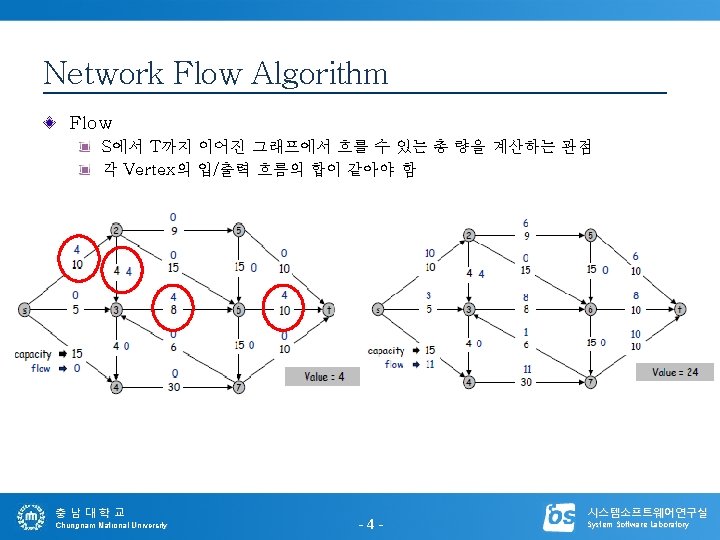
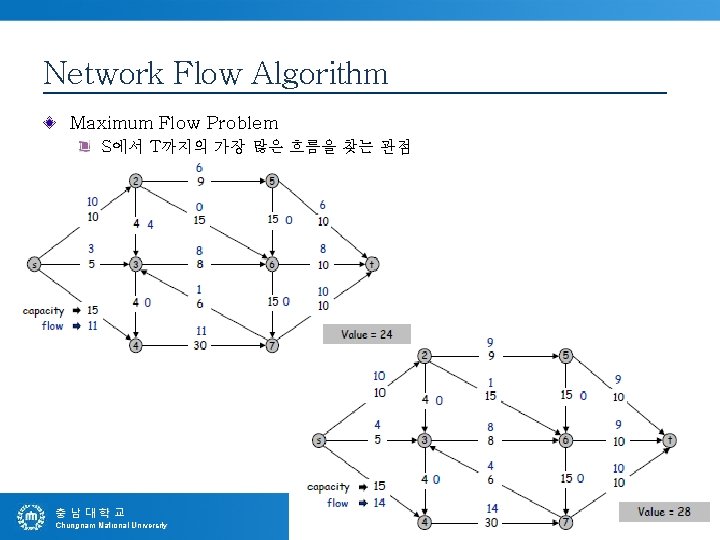
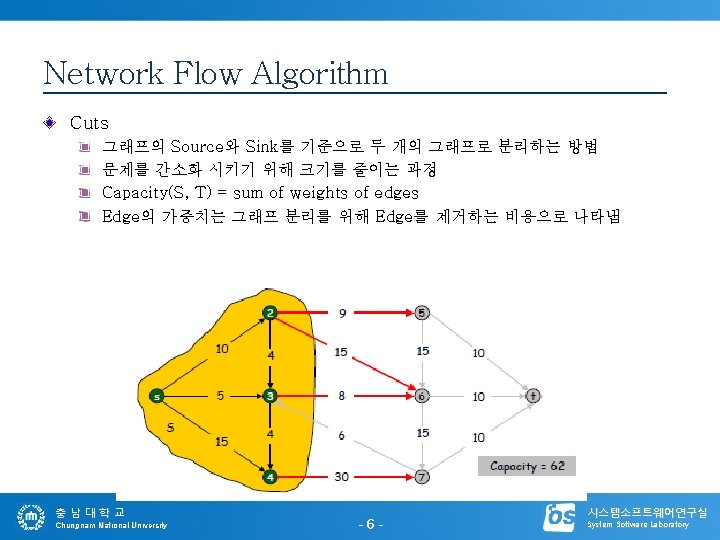
Network Flow Algorithm Maximum Flow Problem S에서 T까지의 가장 많은 흐름을 찾는 관점 충남대학교 Chungnam National University -5 - 시스템소프트웨어연구실 System Software Laboratory


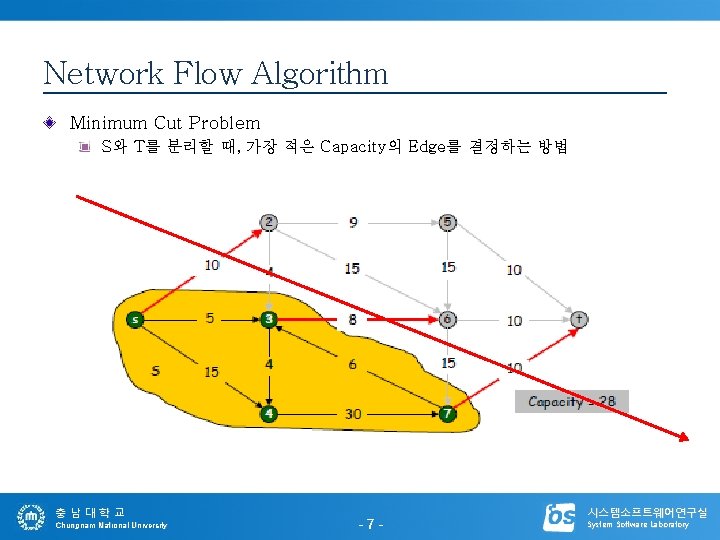
Network Flow Algorithm Minimum Cut Problem S와 T를 분리할 때, 가장 적은 Capacity의 Edge를 결정하는 방법 충남대학교 Chungnam National University -7 - 시스템소프트웨어연구실 System Software Laboratory

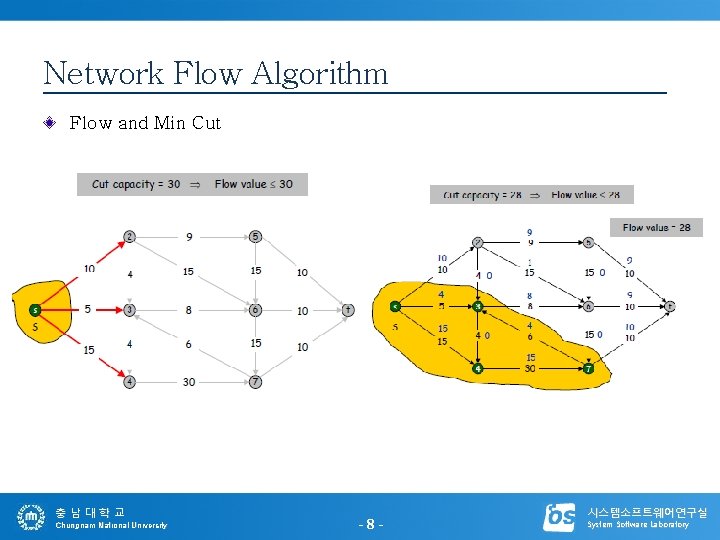
Network Flow Algorithm Flow and Min Cut 충남대학교 Chungnam National University -8 - 시스템소프트웨어연구실 System Software Laboratory

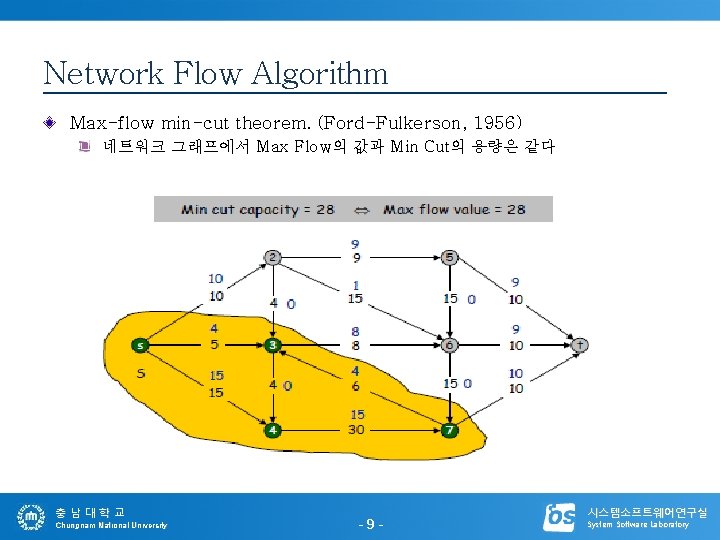
Network Flow Algorithm Max-flow min-cut theorem. (Ford-Fulkerson, 1956) 네트워크 그래프에서 Max Flow의 값과 Min Cut의 용량은 같다 충남대학교 Chungnam National University -9 - 시스템소프트웨어연구실 System Software Laboratory

Algorithms m = Edge n = Vertex Solutions of Complexity Linear programming Ford-Fulkerson Algorithm Edmonds-Karp Algorithm (1972) – O(m 2 n) Dinic’s blocking flow algorithm MPM Algorithm (1978) – O(n 3) Malhotra, Promodh-Kumar and Maheshwari Dinic’s Algorithm General Push-relabel Maximum flow Algorithm Push-relabel algorithm with FIFO vertex selection rule Push-relabel algorithm with dynamic trees KRT(King, Rao, Tarjan) Algorithm James B Orlin’s + KRT’s Algorithm (2013) – O(mn) 충남대학교 Chungnam National University - 10 - 시스템소프트웨어연구실 System Software Laboratory

Edmonds-Karp (1972) m = Edge n = Vertex Maximum Flow Algorithm Ford-Fulkerson 알고리즘 구현 방법의 한 종류 반복을 통해 효과적인 경로를 찾는 방법 BFS(Breath-First Search) 를 사용하여 경로 검색 O(m 2 n) = O(VE 2) 충남대학교 Chungnam National University - 11 - 시스템소프트웨어연구실 System Software Laboratory
![algorithm Edmonds Karp input C1 n 1 n Capacity matrix T1 algorithm Edmonds. Karp input: C[1. . n, 1. . n] (Capacity matrix) T[1. .](https://slidetodoc.com/presentation_image_h2/5f2534f3e701683bd8c0a7d0affea713/image-12.jpg)
algorithm Edmonds. Karp input: C[1. . n, 1. . n] (Capacity matrix) T[1. . n, 1. . n] (Residual matrix. T is equal to C initially) s (Source) t (Sink) output: f (Value of maximum flow) F (A matrix giving a legal flow with the maximum value) f : = 0 (Initial flow is zero) F : = array(1. . n, 1. . n) (Flow matrix) forever m, P : = Breadth. First. Search(C, T, s, t, F) if m = 0 break f : = f + m (Backtrack search, and write flow) v : = t while v ≠ s u : = P[v] F[u, v] : = F[u, v] + m F[v, u] : = F[v, u] - m T[u, v] : = T[u, v] - m T[v, u] : = T[v, u] + m v : = u return (f, F) 충남대학교 Chungnam National University - 12 - 시스템소프트웨어연구실 System Software Laboratory

James B. Olrin. + KRT Algorithm (2013) Max Flows in O(nm) = O(VE) Time, or Better O(nm + m 31/16 log 2 n( KRT(King, Rao, Tarjan, 1994) 알고리즘을 개선하여 성능을 높인 것 m = Edge n = Vertex A Faster Deterministic Maximum Flow Algorithm O(mn + n 2 log 2 n) , O(EV + V 2 log 2 V) 충남대학교 Chungnam National University - 13 - 시스템소프트웨어연구실 System Software Laboratory

Procedure Improve-approx-2(r, S, T ); . 01 Δ : = r(S, T; ( 02. let C be the number of Δ-critical nodes; 03. if C ≥ m 9/16 then let Γ = Δ; 04. 05. find a Γ/(8 m)-optimal flow in G[r]; else, if m 1/3 ≤ C <m 9/16 then let Γ = Δ; 06. let Gc denote the Γ-compact network; 07. find a Γ/(16 m)-optimal flow y on Gc; 08. let y be the induced Γ/(8 m)-opt flow on G[r]; 09. update the residual capacities; 10. else, if C <m 1/3 then 11. choose the minimum value Γ such that 12. the number C of Γ-critical nodes in the 13. network is less than m 1/3; 14. let Gc denote the Γ-compact network; 15. find an optimal flow y on Gc; 16. let y’ be the induced Γ/(16 m)-opt flow in G[r]; 17. update the residual capacities; 충남대학교 Chungnam National University - 14 - 시스템소프트웨어연구실 System Software Laboratory

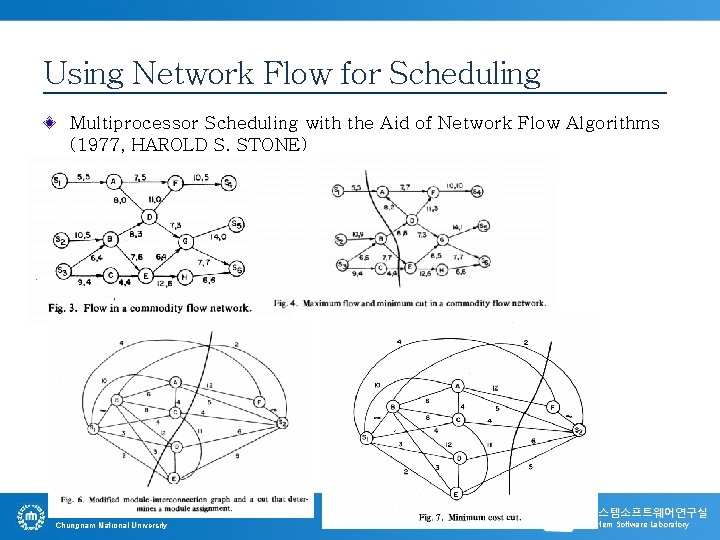
Using Network Flow for Scheduling Multiprocessor Scheduling with the Aid of Network Flow Algorithms (1977, HAROLD S. STONE) 충남대학교 Chungnam National University - 15 - 시스템소프트웨어연구실 System Software Laboratory

Scheduling tasks with ready times and deadlines to minimize average error(1989, W. Shih, J. S. W. Liu, J. Chung, D. W. Gillies) 충남대학교 Chungnam National University - 16 - 시스템소프트웨어연구실 System Software Laboratory

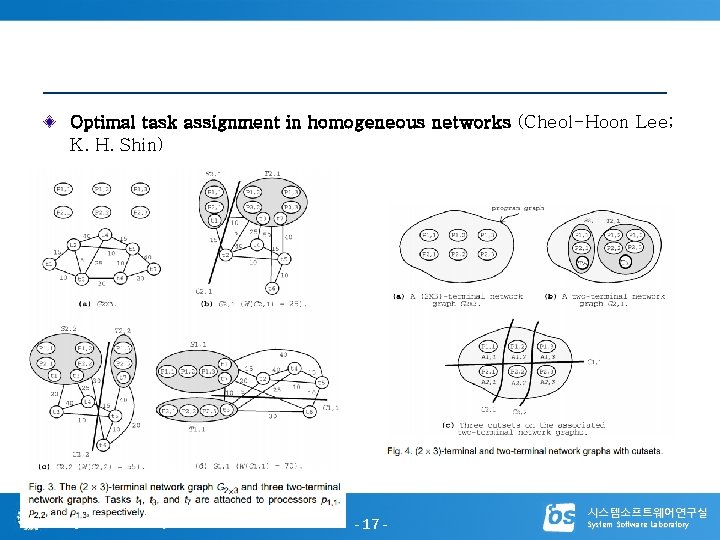
Optimal task assignment in homogeneous networks (Cheol-Hoon Lee; K. H. Shin) 충남대학교 Chungnam National University - 17 - 시스템소프트웨어연구실 System Software Laboratory

충남대학교 Chungnam National University - 18 - 시스템소프트웨어연구실 System Software Laboratory

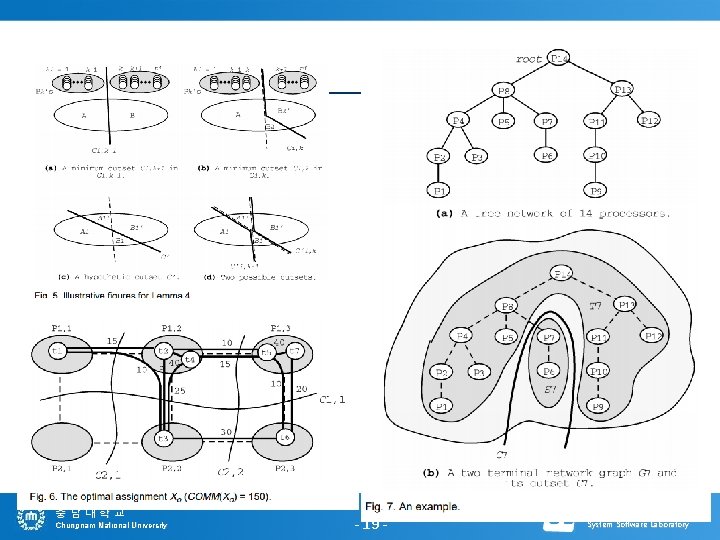
충남대학교 Chungnam National University - 19 - 시스템소프트웨어연구실 System Software Laboratory

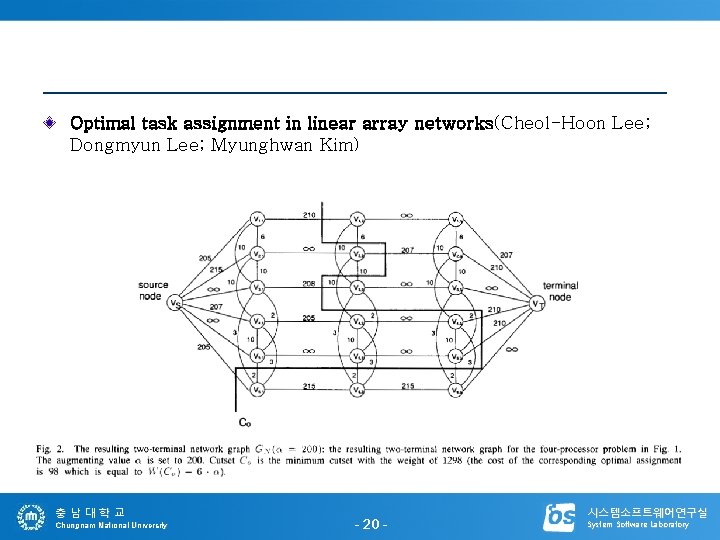
Optimal task assignment in linear array networks(Cheol-Hoon Lee; Dongmyun Lee; Myunghwan Kim) 충남대학교 Chungnam National University - 20 - 시스템소프트웨어연구실 System Software Laboratory

An efficient k-way graph partitioning algorithm for task allocation in parallel computing systems(Cheol-Hoon Lee; M. Kim; C. I. Park) 충남대학교 Chungnam National University - 21 - 시스템소프트웨어연구실 System Software Laboratory

Q&A 감사합니다. 충남대학교 Chungnam National University - 22 - 시스템소프트웨어연구실 System Software Laboratory