Network Clustering Experimental network mapping Graph theory and












- Slides: 35

Network Clustering Experimental network mapping Graph theory and terminology Scale-free architecture Integrating with gene essentiality Robustness Lecturer: Trey Ideker

Measurements of molecular interactions Protein-protein interactions • Yeast-two-hybrid • Kinase-substrate assays • Co-immunoprecipitation w/ mass spec Protein-DNA interactions • Ch. IP-on-chip and Ch. IP-seq Genetic interactions 2 • Systematic Genetic Analysis

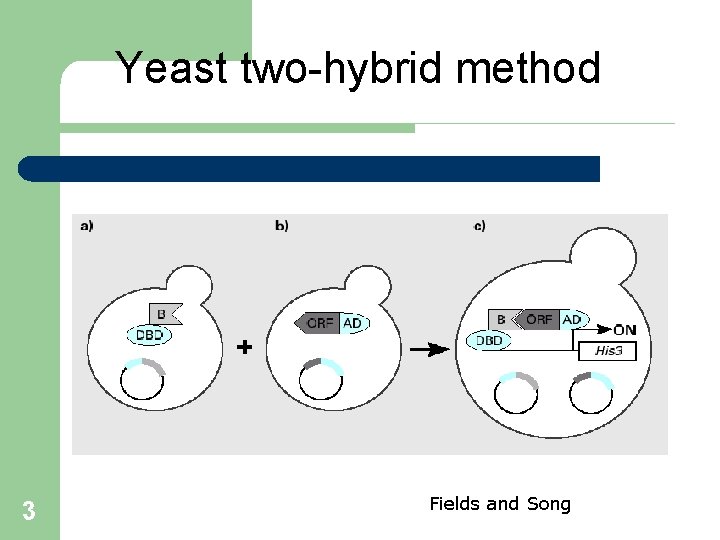
Yeast two-hybrid method 3 Fields and Song

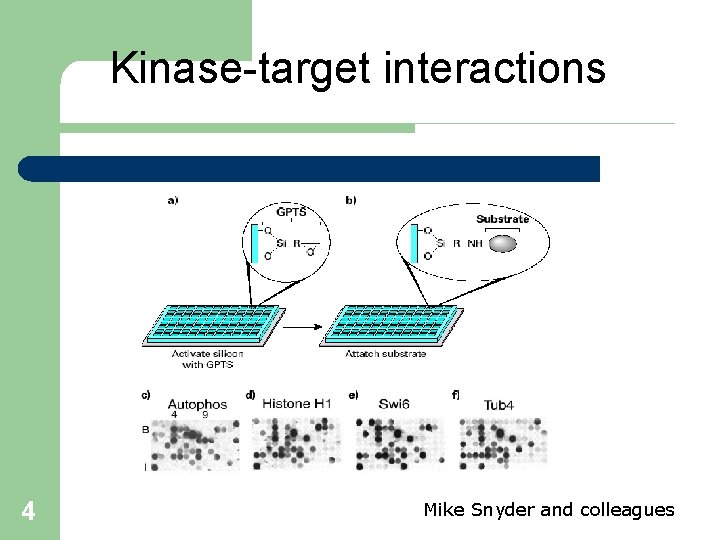
Kinase-target interactions 4 Mike Snyder and colleagues

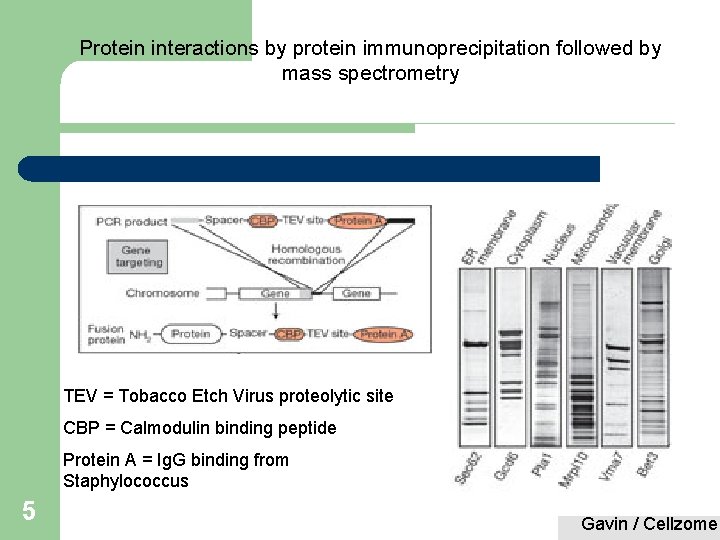
Protein interactions by protein immunoprecipitation followed by mass spectrometry TEV = Tobacco Etch Virus proteolytic site CBP = Calmodulin binding peptide Protein A = Ig. G binding from Staphylococcus 5 Gavin / Cellzome

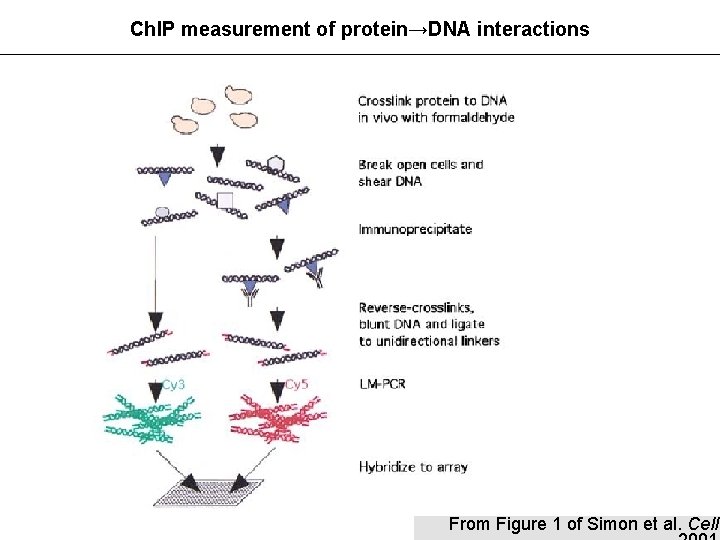
Ch. IP measurement of protein→DNA interactions From Figure 1 of Simon et al. Cell

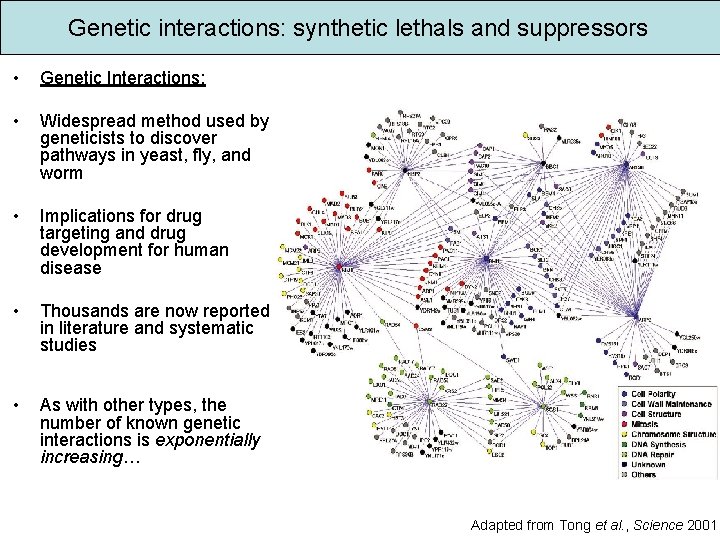
Genetic interactions: synthetic lethals and suppressors • Genetic Interactions: • Widespread method used by geneticists to discover pathways in yeast, fly, and worm • Implications for drug targeting and drug development for human disease • Thousands are now reported in literature and systematic studies • As with other types, the number of known genetic interactions is exponentially increasing… Adapted from Tong et al. , Science 2001

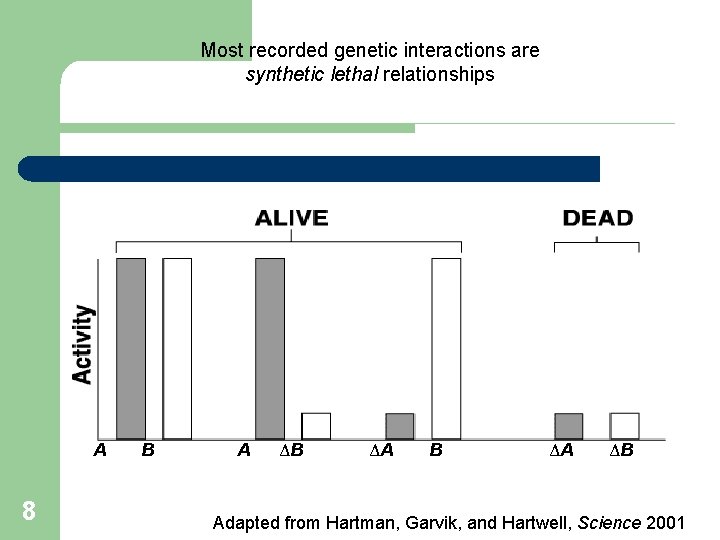
Most recorded genetic interactions are synthetic lethal relationships A 8 B A ΔB ΔA ΔB Adapted from Hartman, Garvik, and Hartwell, Science 2001

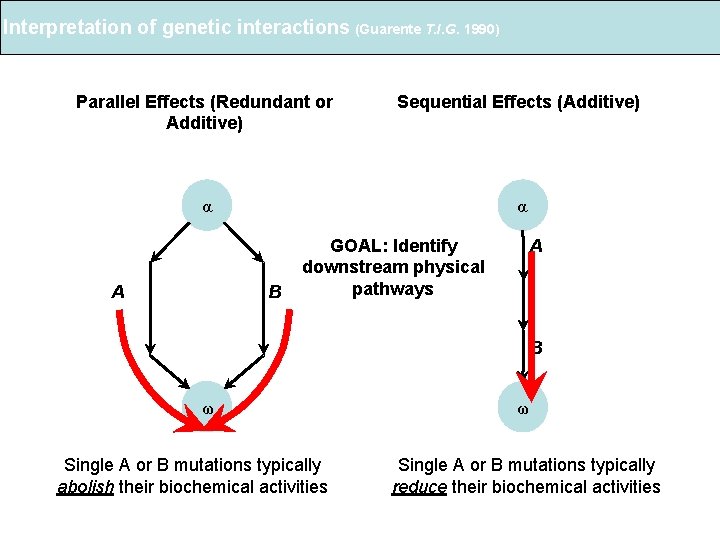
Interpretation of genetic interactions (Guarente T. I. G. 1990) Parallel Effects (Redundant or Additive) Sequential Effects (Additive) α α A B GOAL: Identify downstream physical pathways A B ω Single A or B mutations typically abolish their biochemical activities ω Single A or B mutations typically reduce their biochemical activities

Yeast protein-protein interaction network What are its network properties?

Graphs • Graph G=(V, E) is a set of vertices V and edges E • A subgraph G’ of G is induced by some V’ V and E’ E • Graph properties: – – – – – Node degree Directed vs. undirected Loops Paths Cyclic vs. acyclic Simple vs. multigraph Complete Connected Bipartite

Paths A path is a sequence {x 1, x 2, …, xn} such that (x 1, x 2), (x 2, x 3), …, (xn-1, xn) are edges of the graph. A closed path xn=x 1 on a graph is called a graph cycle or circuit.

Network measures • Degree ki The number of edges involving node i • Degree distribution P(k) The probability (frequency) of nodes of degree k • Mean path length The avg. shortest path between all node pairs • Network Diameter “The longest shortest path” How do the above definitions differ between undirected and directed networks?

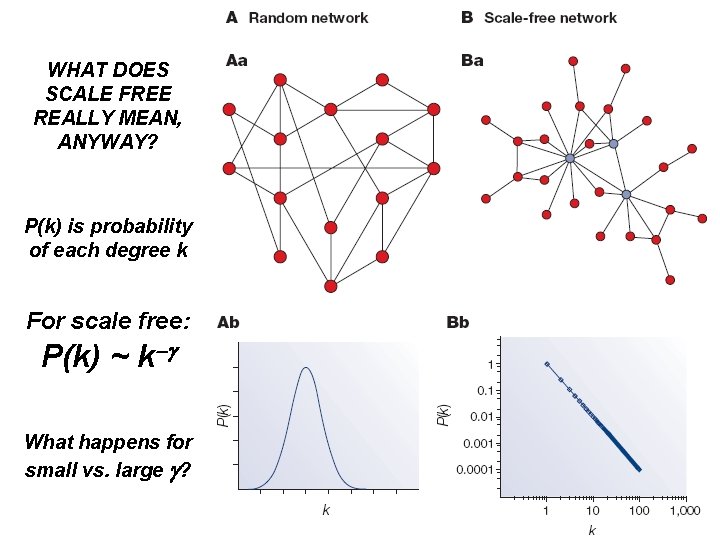
WHAT DOES SCALE FREE REALLY MEAN, ANYWAY? P(k) is probability of each degree k For scale free: P(k) ~ k-g What happens for small vs. large g?

Random vs Preferential Attachment • Erdos-Renyi Start with N nodes and connect each pair with equal probability p • Scale-free Add nodes incrementally. New nodes connect to each existing node I with probability proportional to its degree: Scale-free networks have small avg. path lengths ~ log (log N)– this is called the ‘small world’ effect

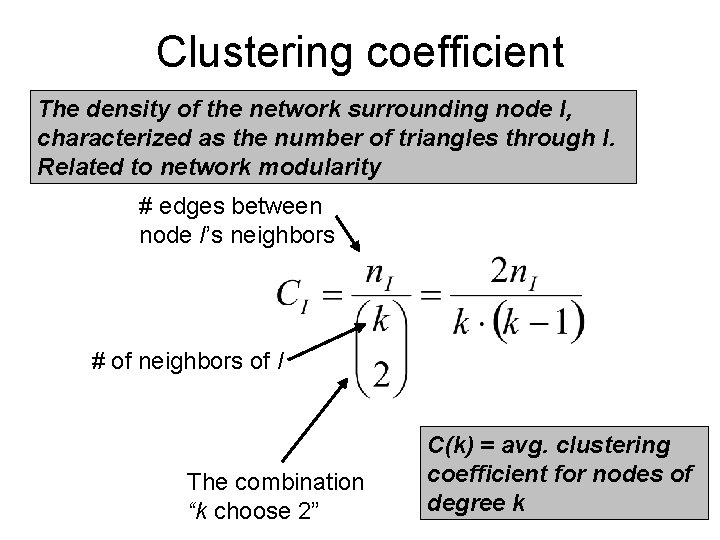
Clustering coefficient The density of the network surrounding node I, characterized as the number of triangles through I. Related to network modularity # edges between node I’s neighbors # of neighbors of I The combination “k choose 2” C(k) = avg. clustering coefficient for nodes of degree k

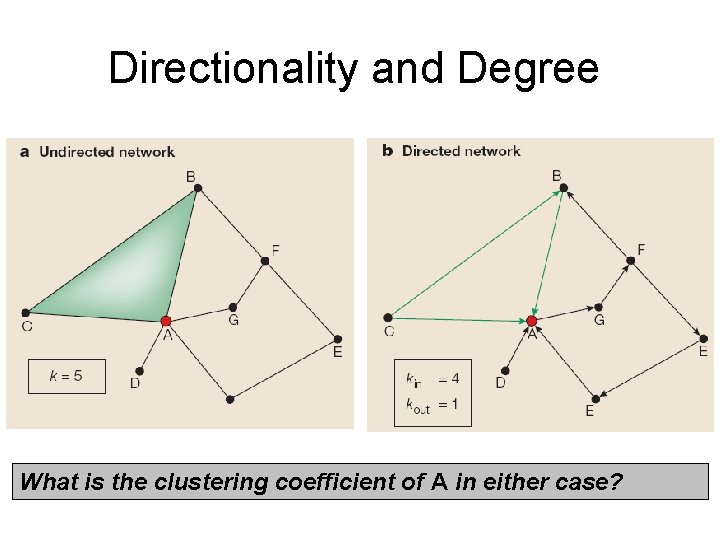
Directionality and Degree What is the clustering coefficient of A in either case?

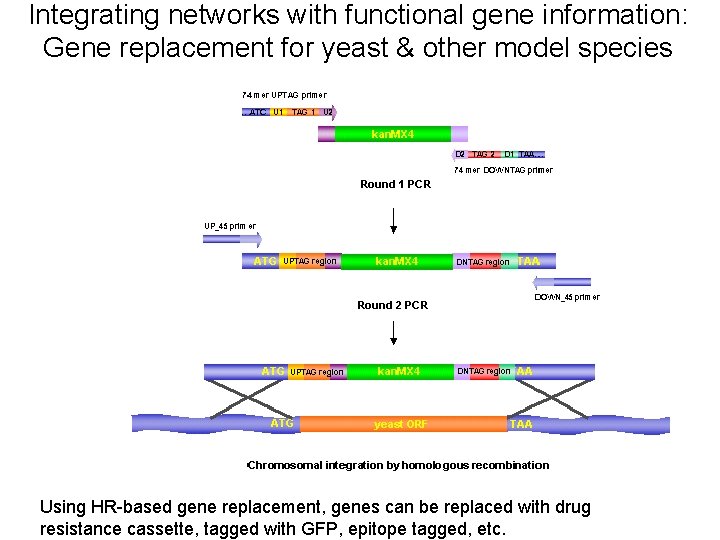
Integrating networks with functional gene information: Gene replacement for yeast & other model species Using HR-based gene replacement, genes can be replaced with drug resistance cassette, tagged with GFP, epitope tagged, etc.

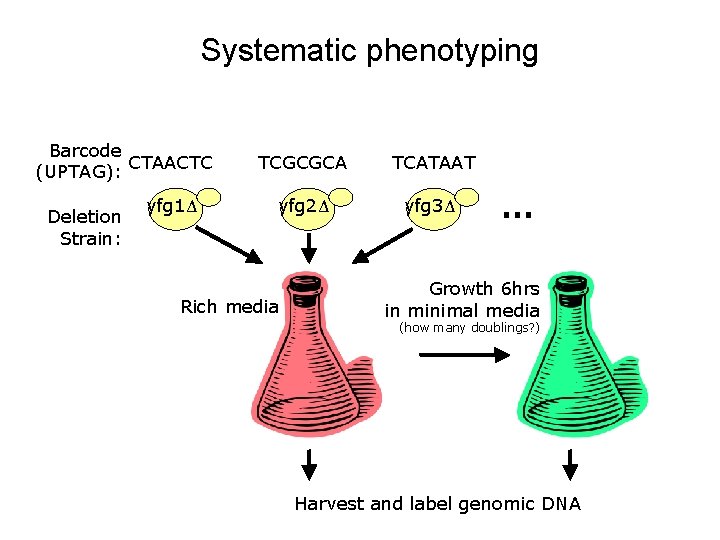
Systematic phenotyping Barcode CTAACTC (UPTAG): Deletion Strain: yfg 1Δ TCGCGCA TCATAAT yfg 2Δ yfg 3Δ Rich media … Growth 6 hrs in minimal media (how many doublings? ) Harvest and label genomic DNA

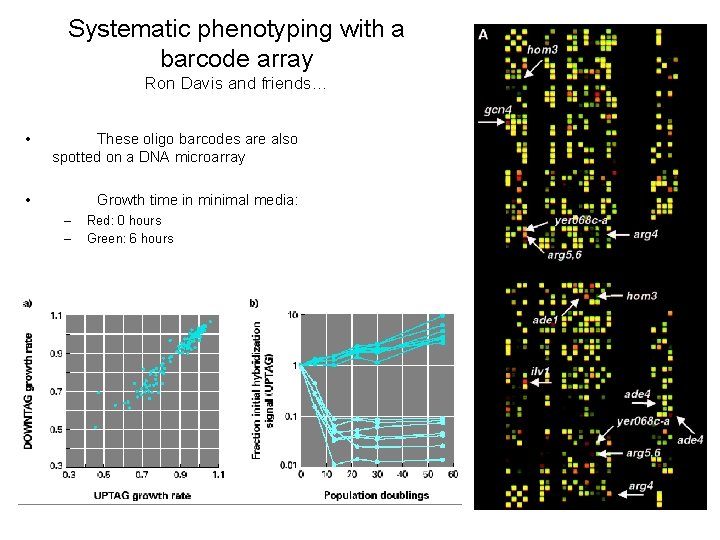
Systematic phenotyping with a barcode array Ron Davis and friends… • These oligo barcodes are also spotted on a DNA microarray • Growth time in minimal media: – – Red: 0 hours Green: 6 hours


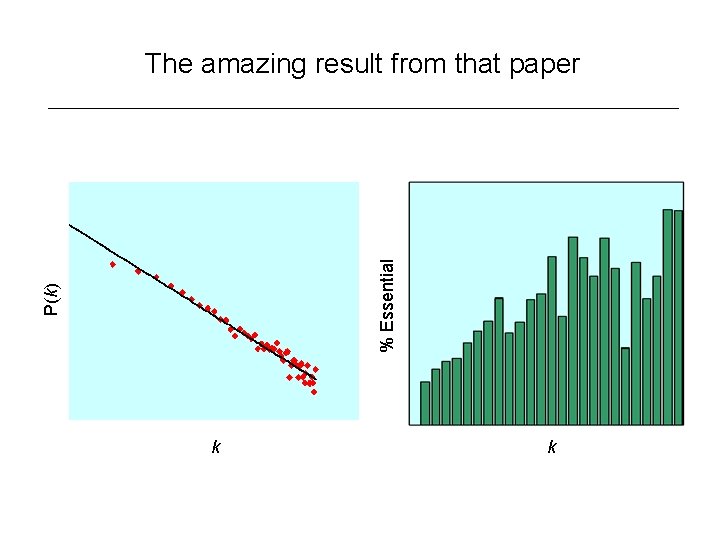
P(k) % Essential The amazing result from that paper k k

Robustness • Complex systems, from the cell to the Internet, can be amazingly resilient to component failure • Network topology plays an important role in this robustness • Even if ~80% of nodes fail, the remaining ~20% still maintain network connectivity • This also leads to attack vulnerability if hubs are selectively targeted • In yeast, only ~20% of proteins are lethal when deleted, and are 5 times more likely to have degree k>15 than k<5.

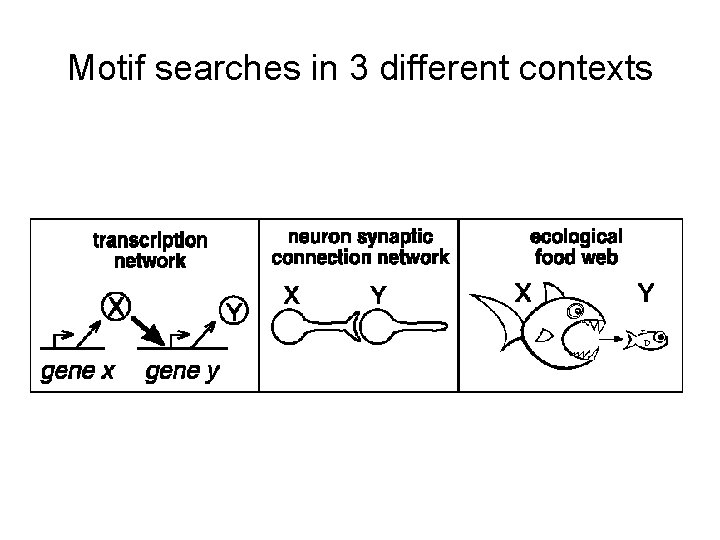
Network Motifs (Milo, Alon et al. ) • Motifs are “patterns of interconnections occurring in complex networks. ” • That is, connected subgraphs of a particular isomorphic topology • The approach queries the network for small motifs (e. g. , of < 5 nodes) that occur much more frequently than would be expected in random networks • Significant motifs have been found in a variety of biological networks and, for instance, correspond to feedforward and feed-back loops that are well known in circuit design and other engineering fields. • Pioneered by Uri Alon and colleagues

Motif searches in 3 different contexts

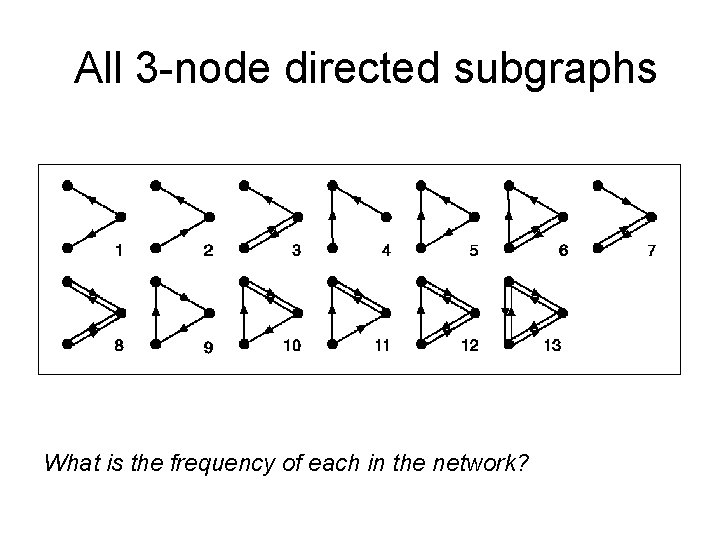
All 3 -node directed subgraphs What is the frequency of each in the network?

Outline of the Approach • Search network to identify all possible n-node connected subgraphs (here n=3 or 4) • Get # occurrences of each subgraph type • The significance for each type is determined using permutation testing, in which the above process is repeated for many randomized networks (preserving node degrees– why? ) • Use random distributions to compute a p-value for each subgraph type. The “network motifs” are subgraphs with p < 0. 001

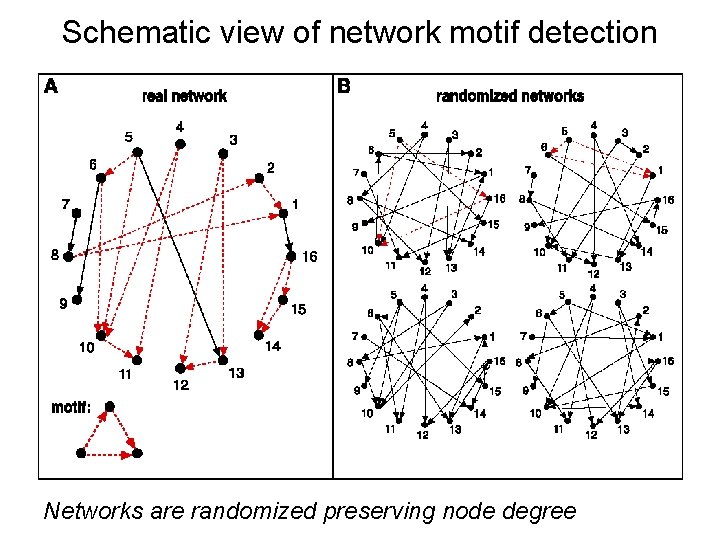
Schematic view of network motif detection Networks are randomized preserving node degree

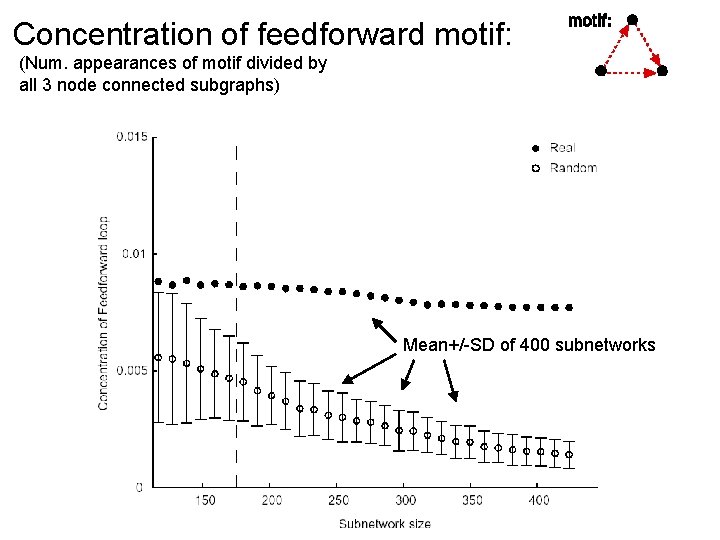
Concentration of feedforward motif: (Num. appearances of motif divided by all 3 node connected subgraphs) Mean+/-SD of 400 subnetworks

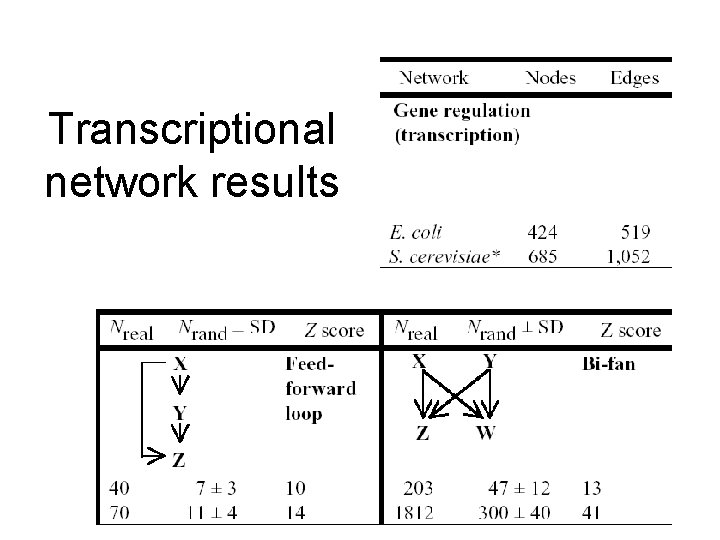
Transcriptional network results

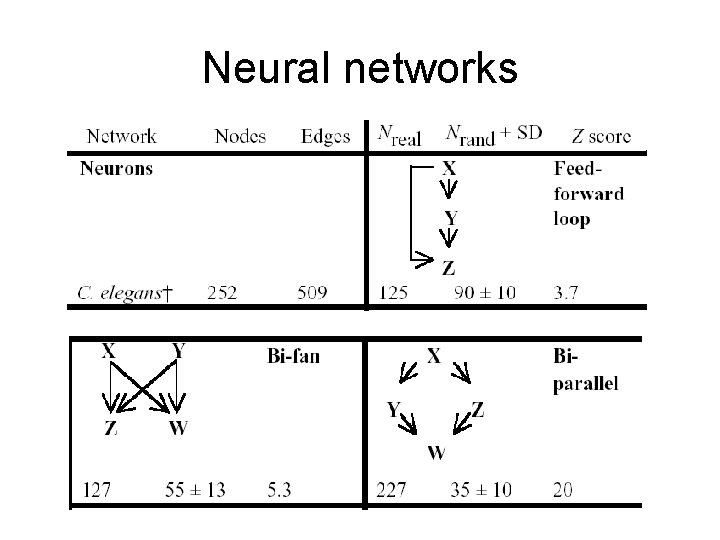
Neural networks

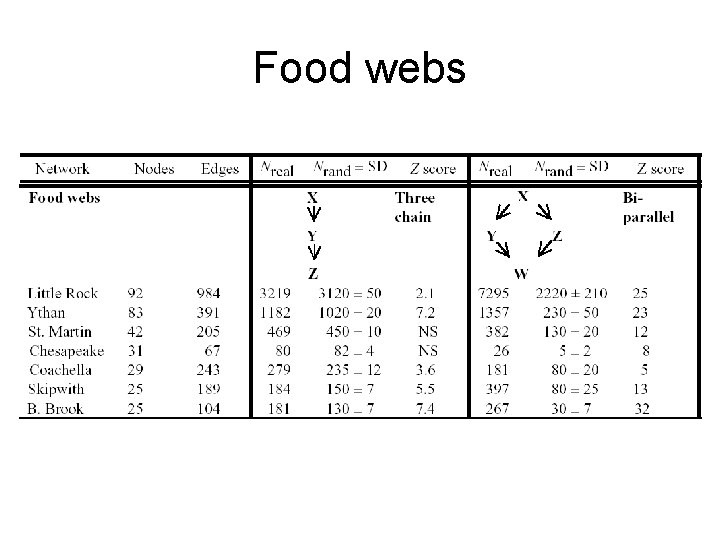
Food webs

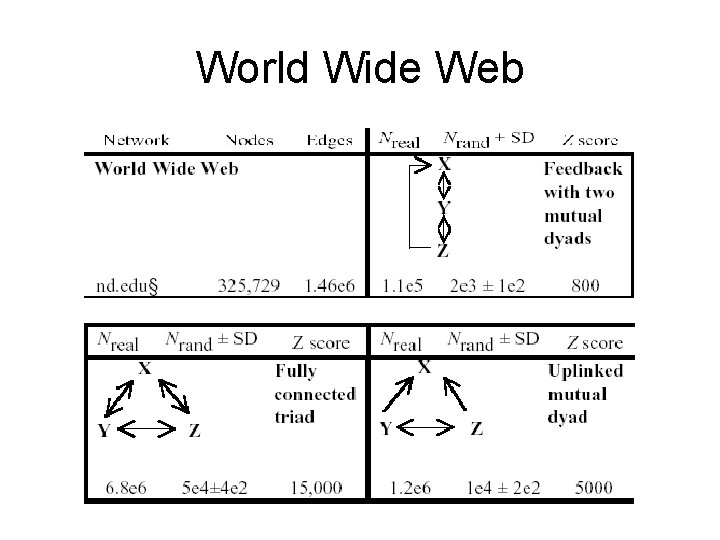
World Wide Web

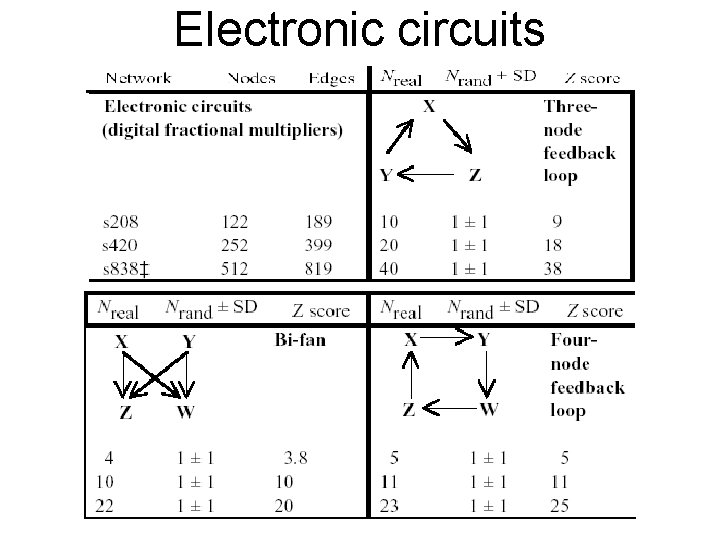
Electronic circuits

Interesting questions • Which networks have motifs in common? • Which networks have completely distinct motifs versus the others? • Does this tell us anything about the design constraints on each network? • E. g. , the feedforward loop may function to activate output only if the input signal is persistent (i. e. , reject noisy or transient signals) and to allow rapid deactivation when the input turns off • E. g. , food webs evolve to allow flow of energy from top to bottom (? !**!? ? ? ), whereas transcriptional networks evolve to process information