Nets 1 Prior Knowledge Rationale 2 Introducing Nets

Nets 1. Prior Knowledge & Rationale 2. Introducing Nets 3. Cuboids 4. Cubes 5. Cones 6. Resources 1

1. Prior Knowledge & Rationale 2

Prior Knowledge: Juice Box Rectangular Rectan Juice gleprism box Nets A 2 -dimensional representation of a 3 -dimensional shape. Cuboi d 3 Carton

Let’s Define it! 4

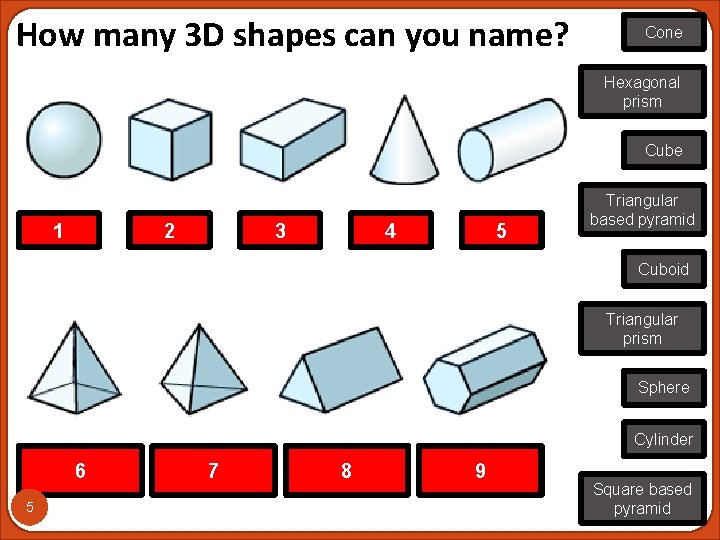
How many 3 D shapes can you name? Cone Hexagonal prism Cube Sphere 1 Cube 2 Cuboid 3 Cone 4 Cylinder 5 Triangular based pyramid Cuboid Triangular prism Sphere Cylinder Square based 6 pyramid 5 Triangular 7 based pyramid Triangular 8 prism Hexagonal 9 prism Square based pyramid

Which of the following are prisms? A D G 6 B E C F H

Which of the following are prisms? • A solid object that has two identical ends and all flat sides. • The cross section is the same all along its length. • The shape of the ends give the prism a name, such as "triangular prism" 7

2. Introducing Nets Introducing nets & their development 8

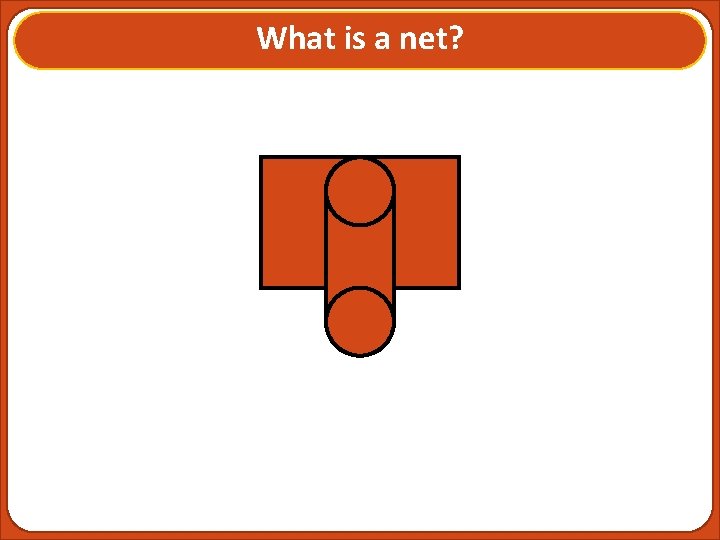
What is a net? A 2 -dimensional representation of a 3 -dimensional shape.

Student’s CD 10

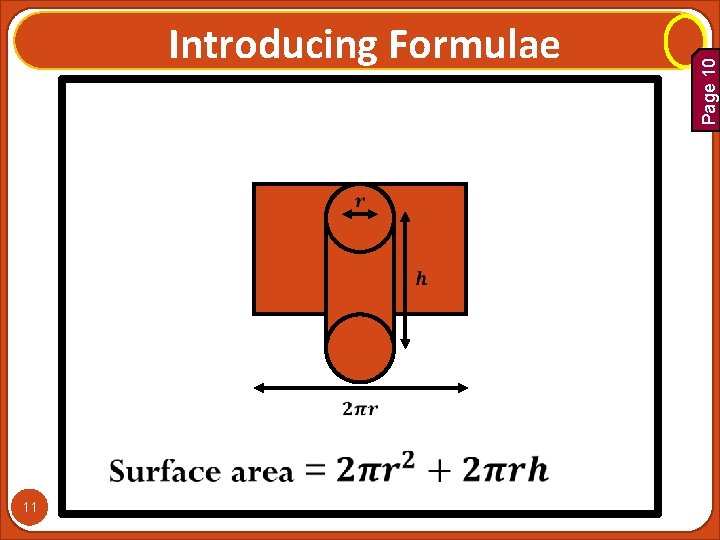
11 Page 10 Introducing Formulae

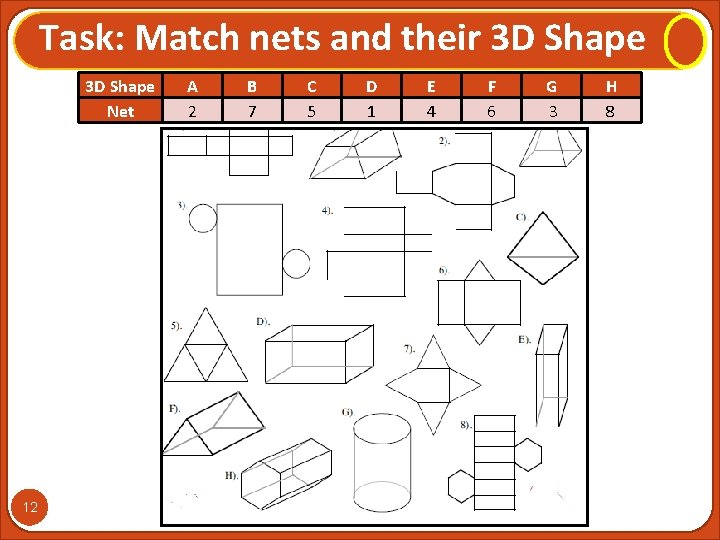
Task: Match nets and their 3 D Shape Net 12 A 2 B 7 C 5 D 1 E 4 F 6 G 3 H 8

Spatial Reasoning ? ? �Spatial Reasoning is not a natural ability �Which is the easiest to go from a Solid to a net OR a net to a Solid? �Research says a solid to a net is harder �What do you think? Does it depend on the solid and how familiar you are with it �Link back to previous slide 13

3. Cuboids 14

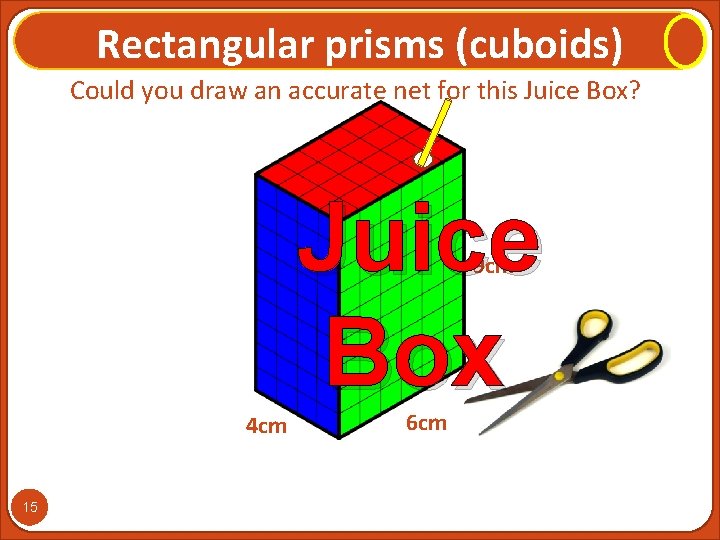
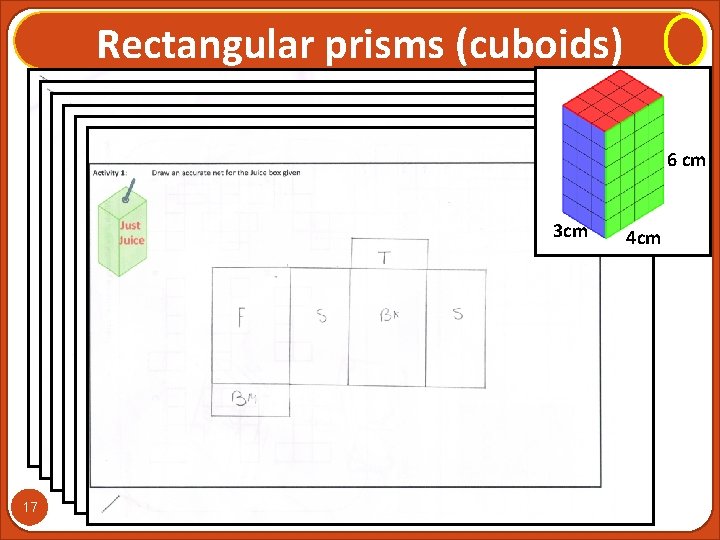
Rectangular prisms (cuboids) Could you draw an accurate net for this Juice Box? Juice Box 9 cm 4 cm 15 6 cm

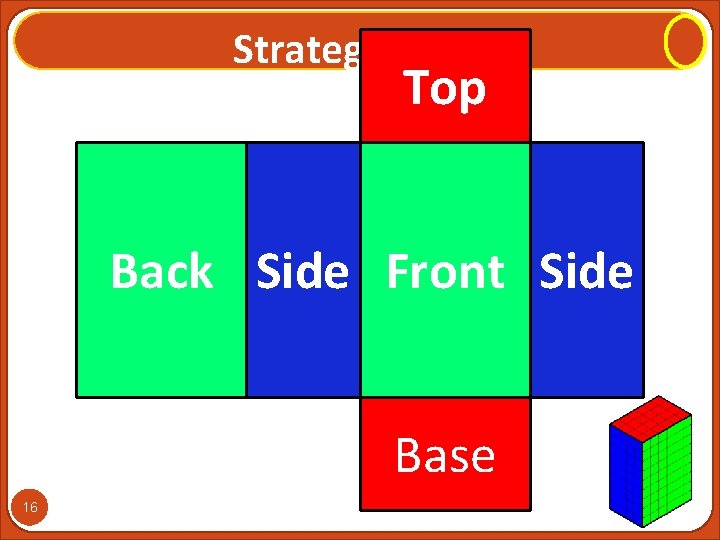
Strategy Used Top C Back A Side B Front A Side B 16 Base C

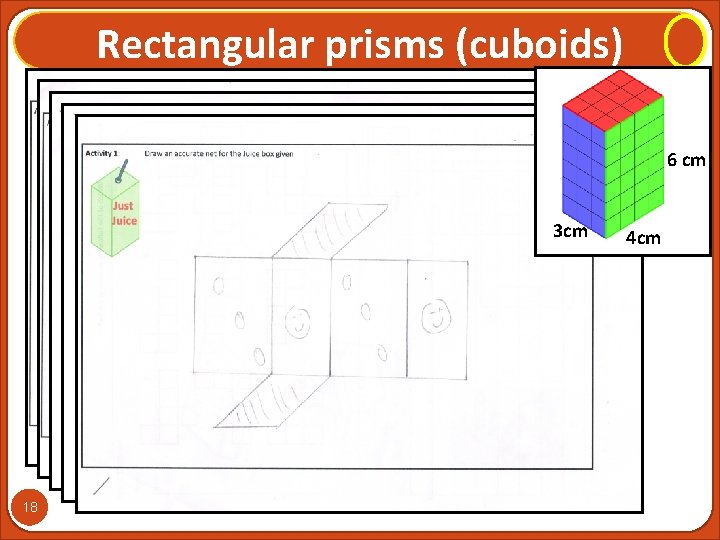
Rectangular prisms (cuboids) 6 cm 3 cm 17 4 cm

Rectangular prisms (cuboids) 6 cm 3 cm 18 4 cm

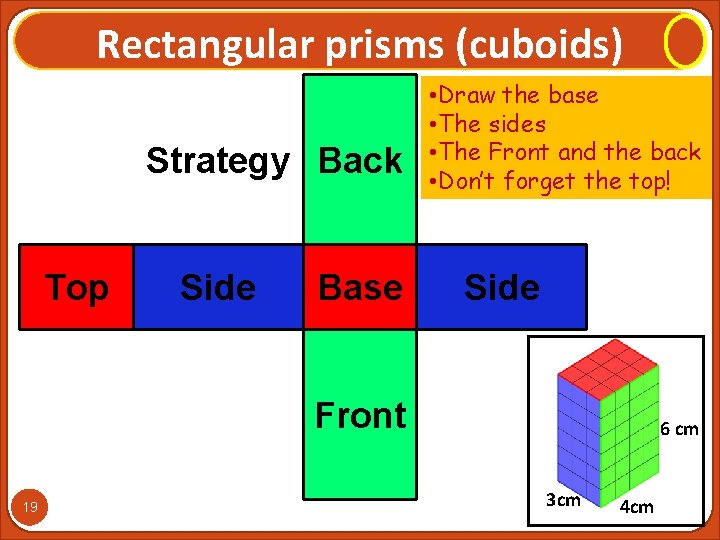
Rectangular prisms (cuboids) Strategy Back Top Side Base • Draw the base • The sides • The Front and the back • Don’t forget the top! Side Front 19 6 cm 3 cm 4 cm

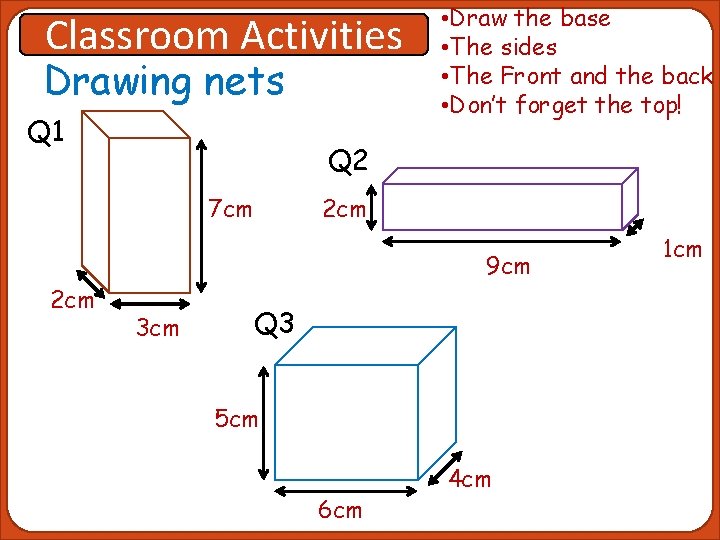
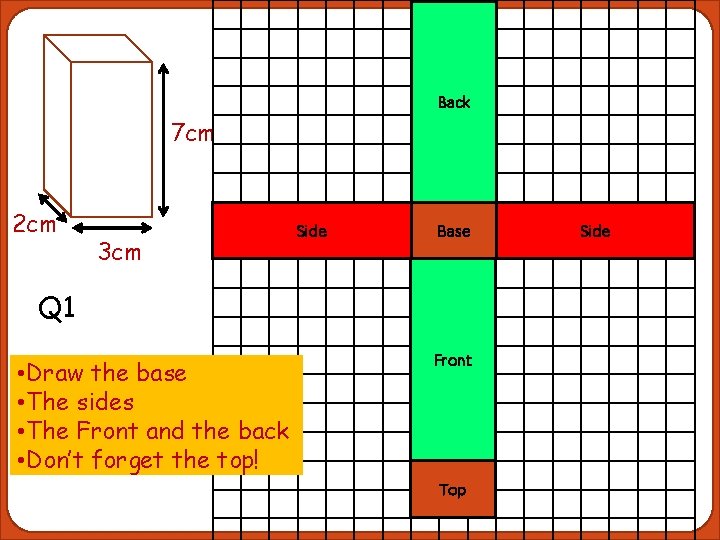
Classroom Activities Drawing nets Q 1 • Draw the base • The sides • The Front and the back • Don’t forget the top! Q 2 7 cm 2 cm 9 cm 2 cm 3 cm Q 3 5 cm 6 cm 4 cm 1 cm

Back 7 cm 2 cm 3 cm Side Base Q 1 • Draw the base • The sides • The Front and the back • Don’t forget the top! Front Top Side

Connections in Mathematics Within Curriculum Strands Subjects Real Past World Future Across Strands

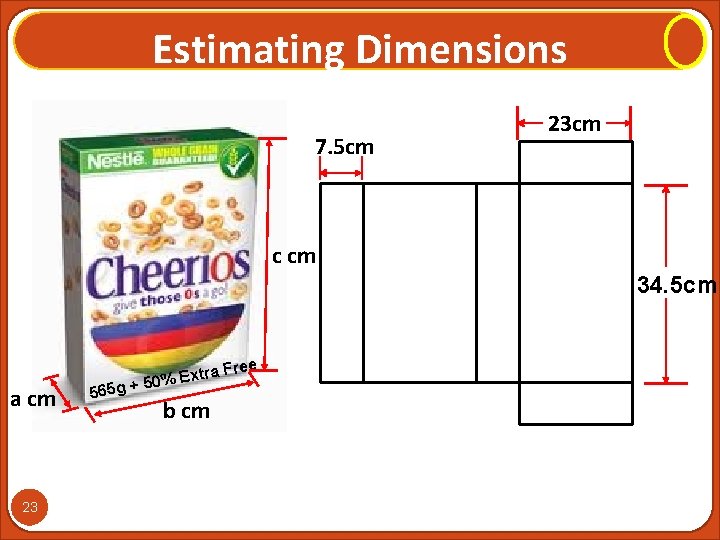
Estimating Dimensions 7. 5 cm 23 cm c cm 34. 5 cm a cm 23 565 g + xtra F E % 0 5 b cm ree

Estimate the dimension of the Coco Pops box c cm ree 565 g + 26 xtra F E % 0 5 a cm b cm

Estimating Dimensions a c i ess J n h Jo 27

Summary �Cuboids �Nets �Students’ Misconceptions �Connections…Estimating Dimensions etc 28

4. Cubes 29

Can you draw the net of a Cube? 30

Compare yours to the person next to you 31

Solids to Nets to Solids 32

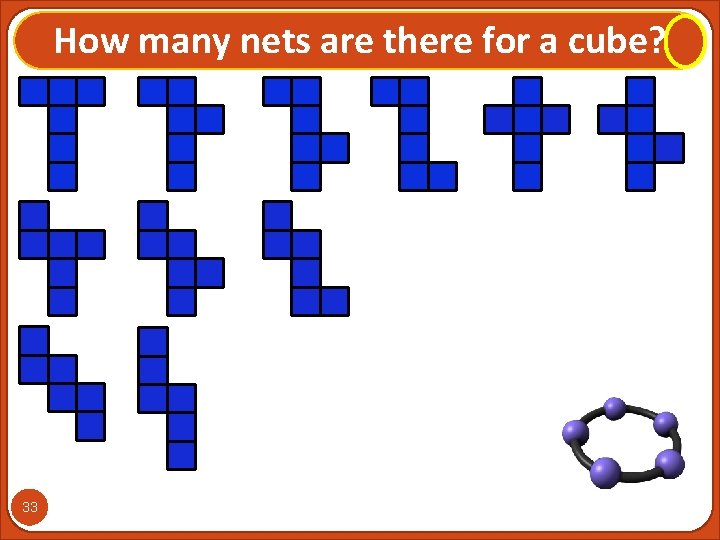
How many nets are there for a cube? 33

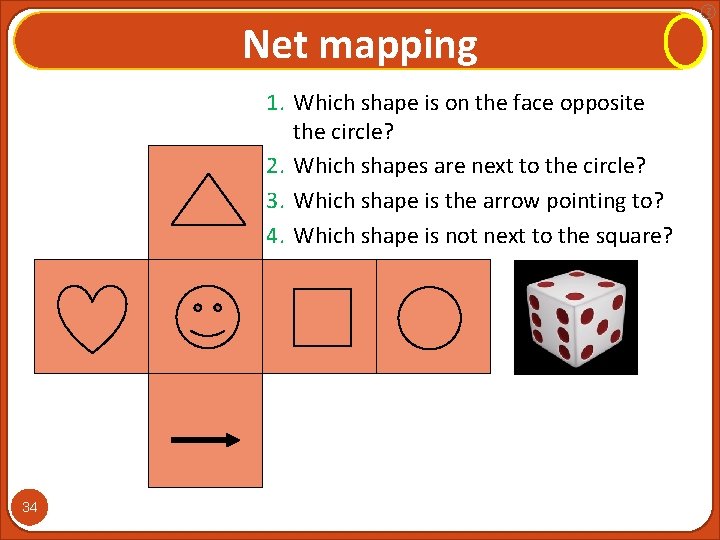
Net mapping 1. Which shape is on the face opposite the circle? 2. Which shapes are next to the circle? 3. Which shape is the arrow pointing to? 4. Which shape is not next to the square? 34 Z

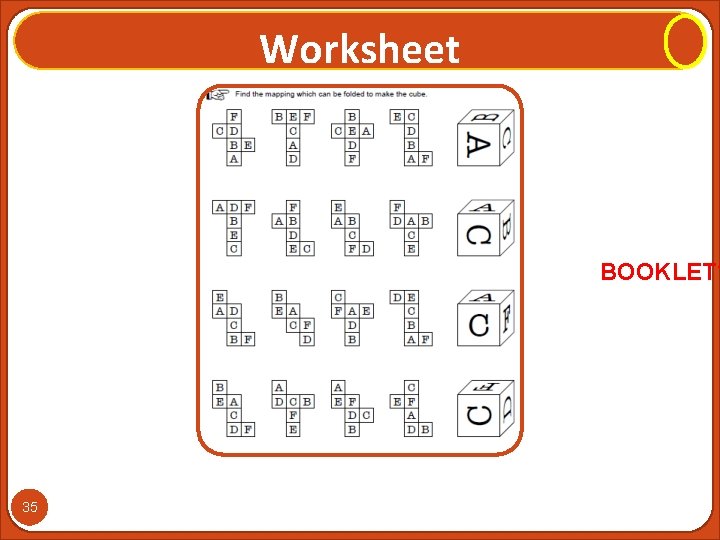
Worksheet BOOKLET? 35

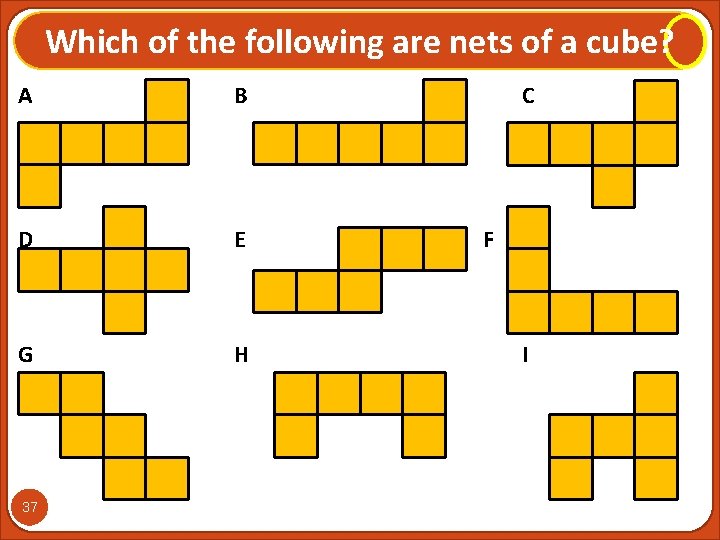
Which of the following are nets of a cube? A B D E C F BOOKLET? G 36 H I

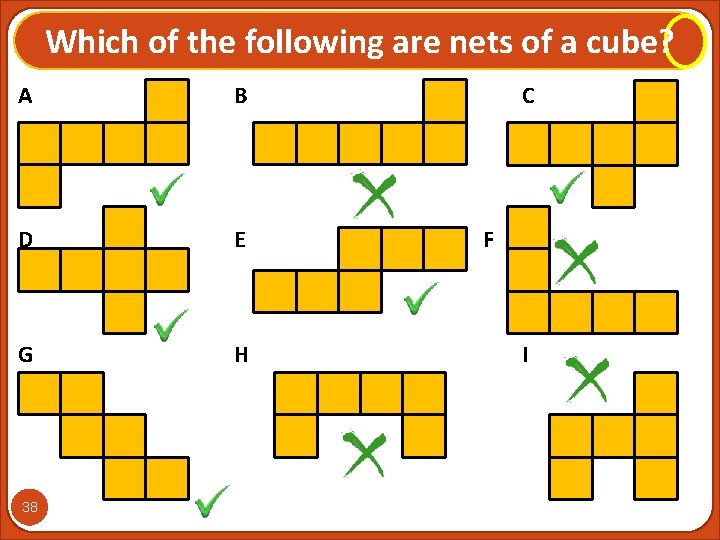
Which of the following are nets of a cube? A B D E G H 37 C F I

Which of the following are nets of a cube? A B D E G H 38 C F I

Connections in Mathematics Within Curriculum Strands Subjects Real Past World Future Across Strands

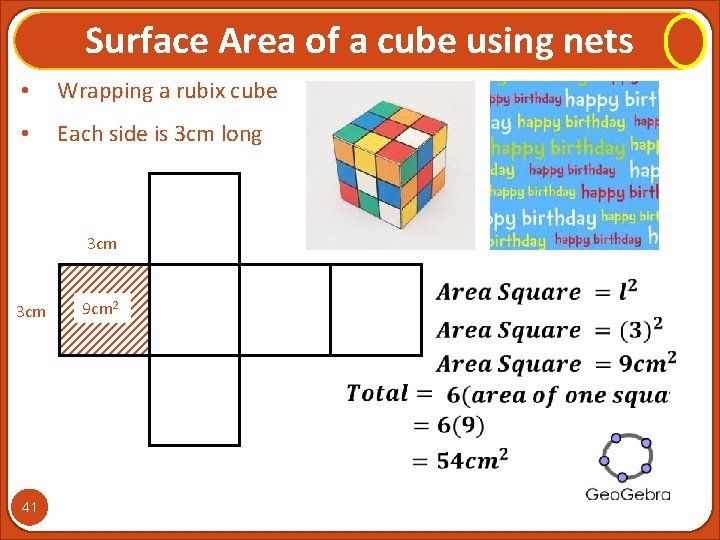
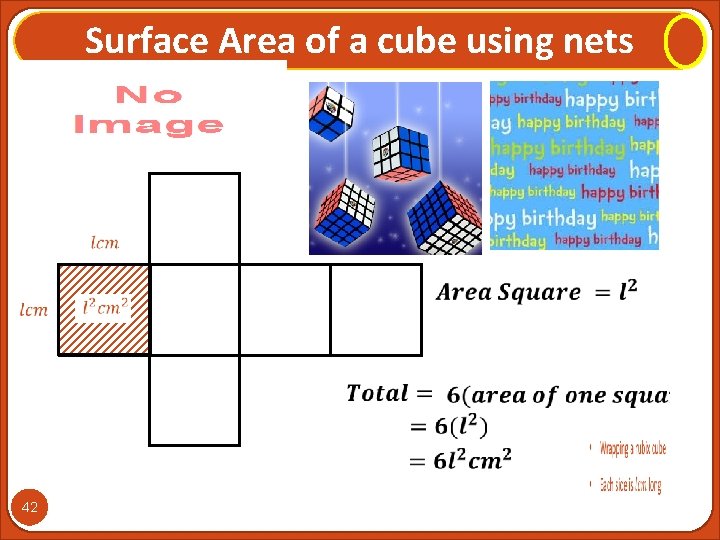
Surface Area of a cube using nets 40

Surface Area of a cube using nets • Wrapping a rubix cube • Each side is 3 cm long 3 cm 41 9 cm 2

Surface Area of a cube using nets 42

Volume of Prisms 43

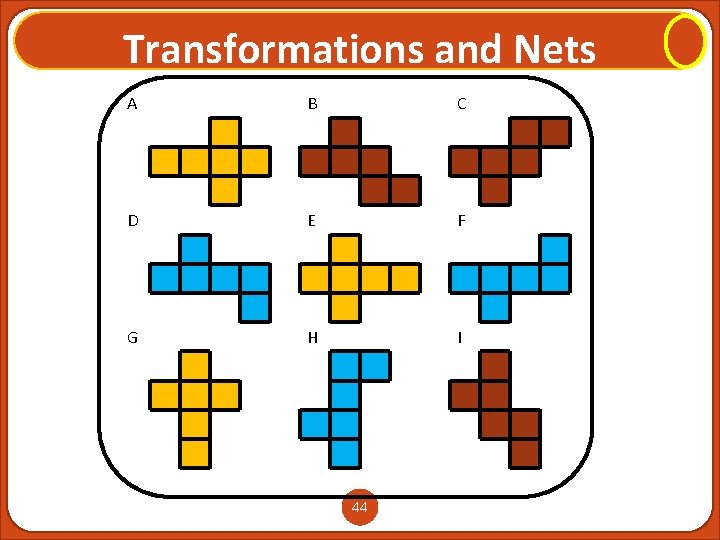
Transformations and Nets A B C D E F G H I 44

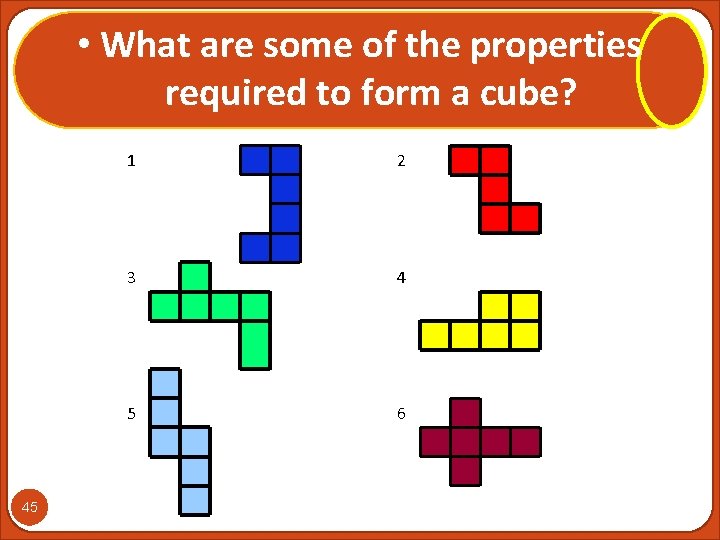
• What are some of the properties required to form a cube? 45 1 2 3 4 5 6

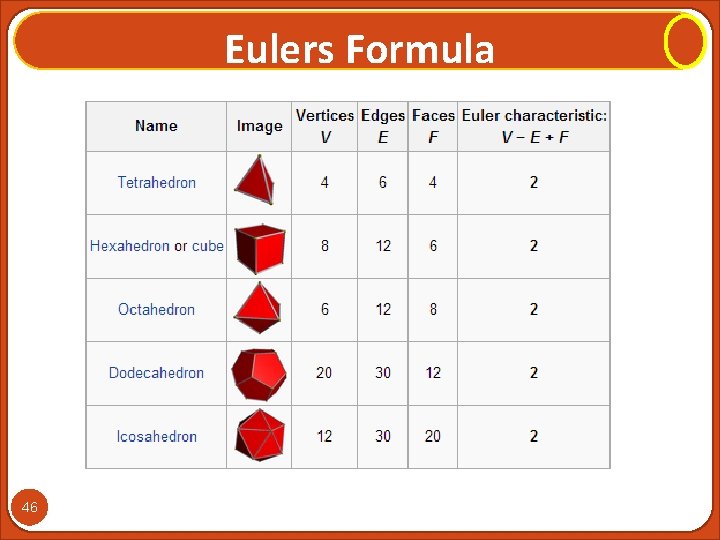
Eulers Formula 46

Summary �Cubes �Nets �Solids �Surface Area �Volume �Transformations �Euler’s Theorem 47

5. Cone Task Po Post 1 st Year How many times has a student mixed up Perpendicular Height and Slant Height? How many times have you retaught it over and over again? NO Longer with one simple question: Build a cone of radius 5 cm and perpendicular height 12 cm 48

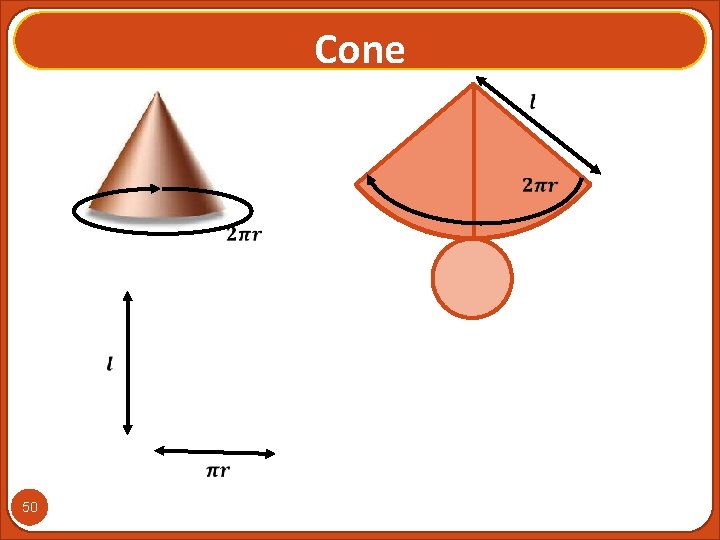
Cone 50

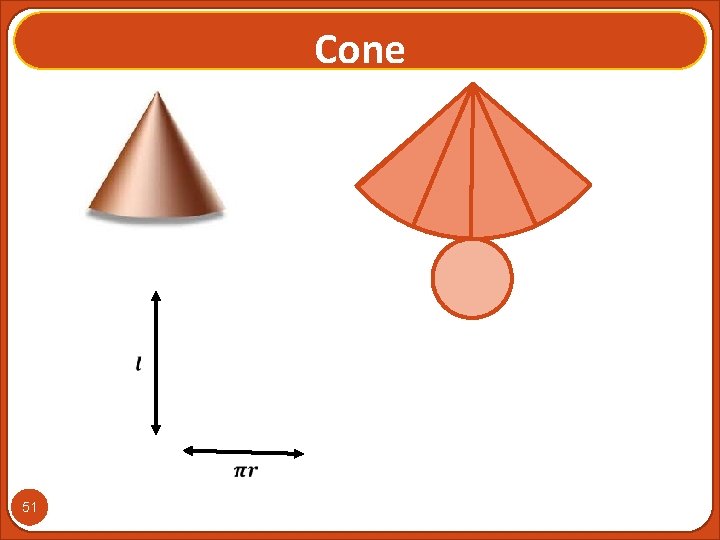
Cone 51

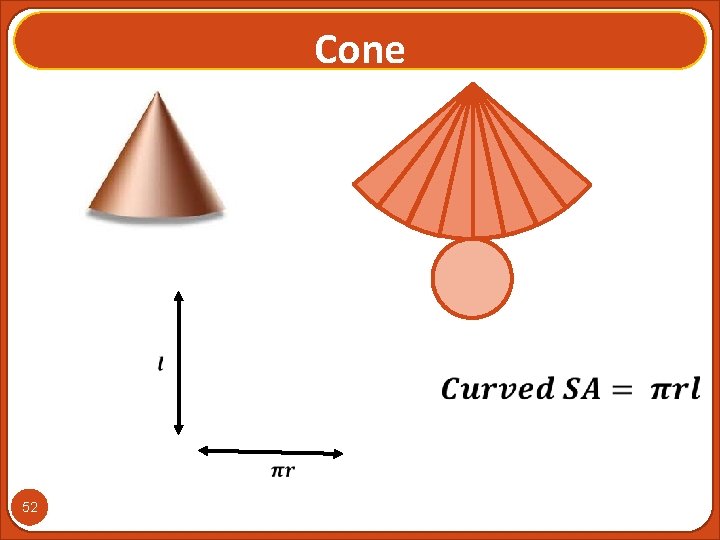
Cone 52

Summary �Cone �Slant Height �Perpendicular Height �Problem Solving �Pythagoras’ Theorem �Curved Surface Area Formula �Angles �Psychomotor skills 53