Nested Logit Models GEV models have the advantage











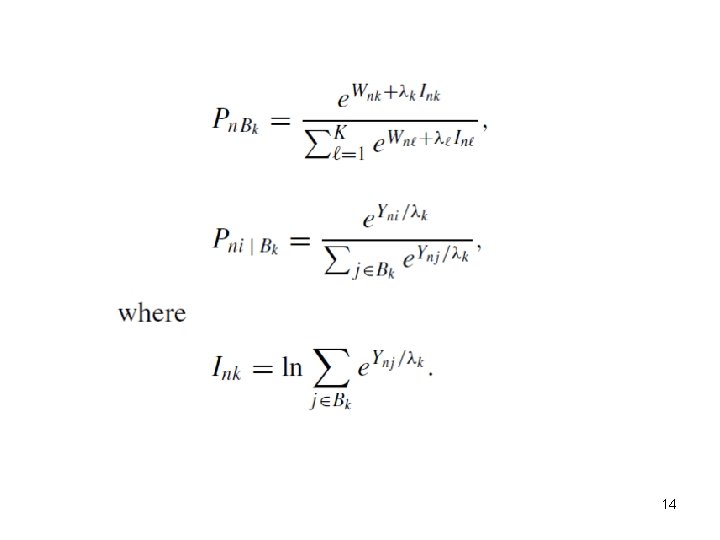











![NL in Biogeme • Specify nesting structure [NLNests] // Name paramvalue Lower. Bound Upper. NL in Biogeme • Specify nesting structure [NLNests] // Name paramvalue Lower. Bound Upper.](https://slidetodoc.com/presentation_image/5f910758cbf54fcb910341883ddb504d/image-29.jpg)
- Slides: 29

Nested Logit Models

GEV models have the advantage that the choice probabilities usually take a closed form 2

The most widely used member of the GEV family is the Nested Logit 3

4

5

6

7

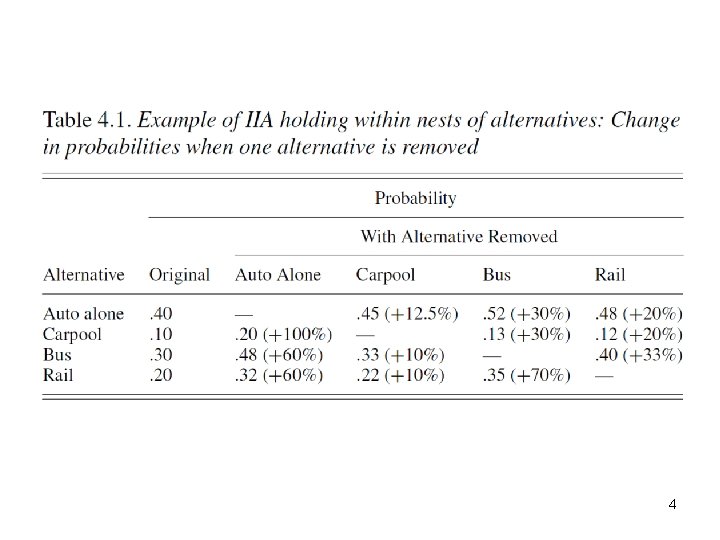
The Problem The common error components creates a covariance between the total error for bus and LRT This covariance violates the assumption underlying the MNL model 8

The choice probabilities for alternative 9

10

11

Decomposing into two Logits 12

13
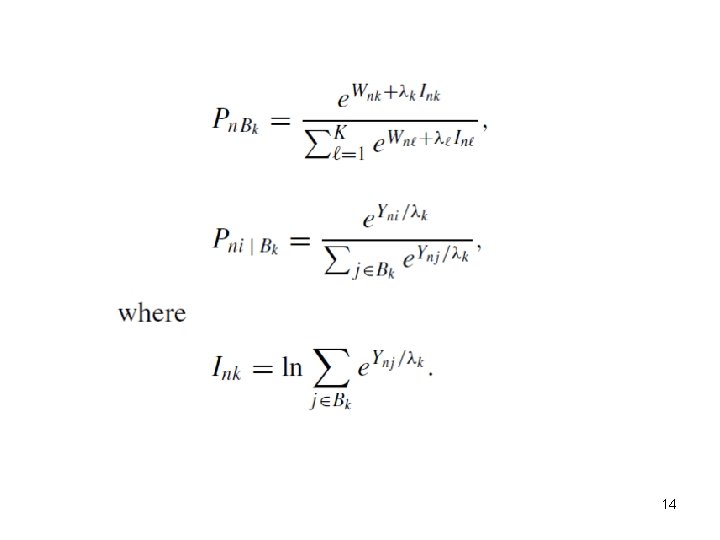
14

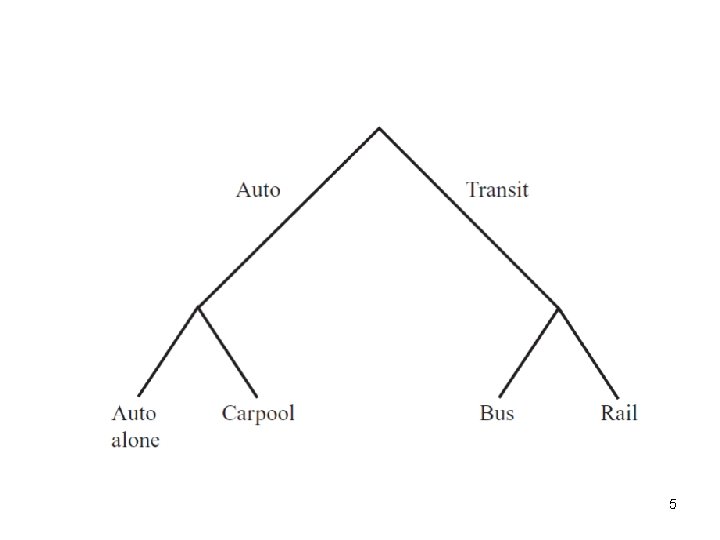
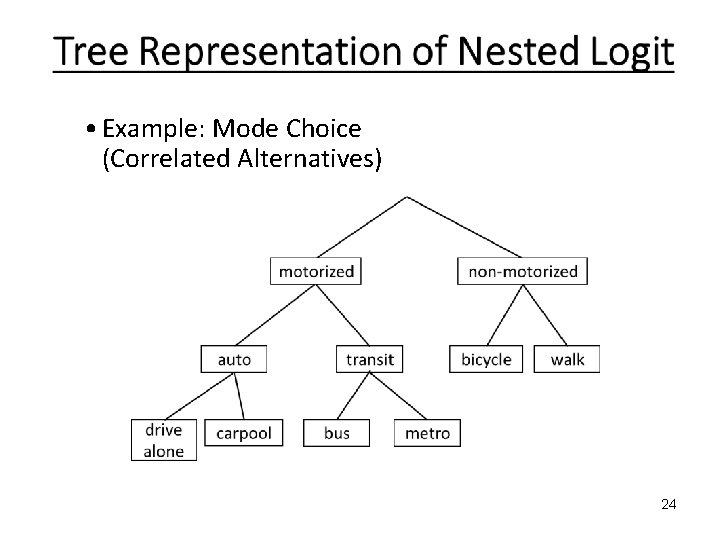
Nested logit model • Group similar alternatives in nests • Two-level choice: – Choice of nest – Choice of alternative within nest 15

Lower level model • Conditional probability • Choice between bus alternatives – Conditional on choice of the nest 16

Upper level model • Choice between car and bus • represents both bus alternatives – Nest systematic utility – Expected value of maximum utility – Define Vbus as the expected maximum utility of red bus 17 and blue bus

Expected maximum utility • For i. i. d Gumbel errors – Inclusive value – Where µb is the scale parameter for the MNL associated with the choice between red bus and blue 18 bus

Choice probabilities 19

Choice probabilities for µb = 1, µ is normalized to 1 20

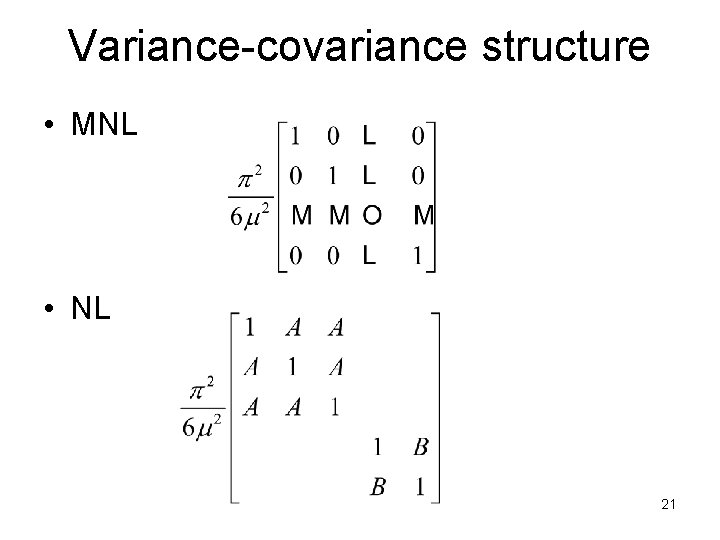
Variance-covariance structure • MNL • NL 21

Simultaneous estimation Sequential estimation: • Estimation of NL decomposed into two estimations of MNL • Estimator is consistent but not efficient Simultaneous estimation: • Log-likelihood function is generally non concave • No guarantee of global maximum • Estimator asymptotically efficient

Simultaneous estimation •

• Example: Mode Choice (Correlated Alternatives) 24

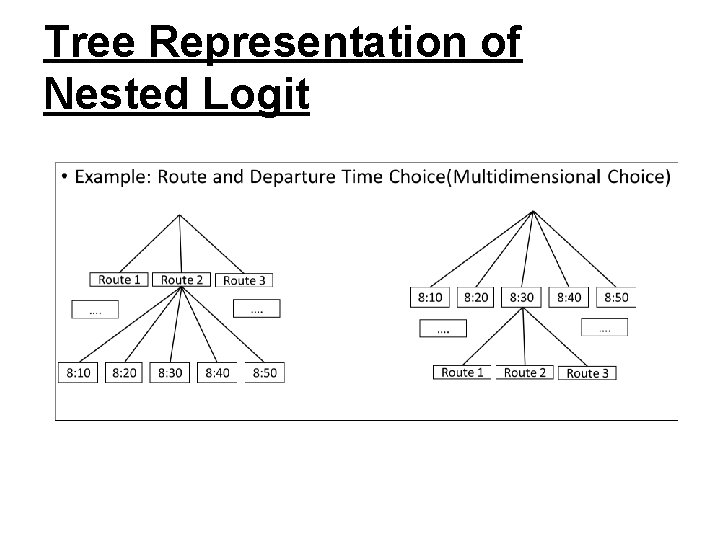
Tree Representation of Nested Logit

Swissmetro example • MNL Parameter Value t-Stat Constant_Train -0. 668 -18. 7 Constant_SM -0. 0162 -0. 52 b_Travel. Time -0. 00790 -21. 7 b_Travel. Cost -0. 0128 -30. 0 26

Swissmetro example (2) • NL: model 1 Parameter Value t-Stat Constant_Train -0. 557 -5. 8 Constant_SM 0. 00976 0. 26 b_Travel. Time -0. 00782 -21. 3 b_Travel. Cost -0. 0125 -26. 2 Sigma 1. 082 1. 13 (vs. 1) 27

Swissmetro example (3) • NL: model 2 Parameter Value t-Stat Constant_Train -0. 372 -18. 7 Constant_SM 0. 00131 0. 05 b_Travel. Time -0. 00629 -20. 0 b_Travel. Cost -0. 00958 -22. 5 Sigma 2. 051 11. 1 (vs. 1) 28
![NL in Biogeme Specify nesting structure NLNests Name paramvalue Lower Bound Upper NL in Biogeme • Specify nesting structure [NLNests] // Name paramvalue Lower. Bound Upper.](https://slidetodoc.com/presentation_image/5f910758cbf54fcb910341883ddb504d/image-29.jpg)
NL in Biogeme • Specify nesting structure [NLNests] // Name paramvalue Lower. Bound Upper. Bound status list of alt Existing 1. 0 1 10 0 1 3 Future 1. 0 1 10 1 2 • Select model [Model] $NL • Nesting constraints [Constraint. Nest. Coef] // (Car. Nest = Bus. Nest) 29