Neighborhood Operations Objectives Why are neighborhoods important What

Neighborhood Operations

Objectives • Why are neighborhoods important? • What is linear convolution? – – discrete templates, masks or filters algorithm mechanics graphical interpretation • Describe non-linear operators – maximum – minimum – median • What is tiling?

Why are neighbourhoods important? pixel

Because… • Provide context for individual pixels. • Relationships between neighbors determine image features. • Neighborhood operations: – noise reduction – edge enhancement – zooming

Noise reduction Edge Enhancement Zooming

Neighbourhood Operations • Linear convolution (*) – A*B*C*D = B*C*D*A = …. • Non-linear operators – median, max, min, . . .

Convolution versus Spectral • We learnt two methods of processing images: – Convolution – Spectral • We analyzed and demonstrated how to build a processor (systolic, pipelined, parallel, cellular automaton) for 1 D convolution. – 1 D convolution is used in speech processing and in polynomial multiplication. • We will use visualized animations now to show in more detail how 2 D convolution works for images. • This should convince you how important it is to do convolution quickly in modern Spectral Architectures, especially for 3 D etc.

2 D Convolution We will show more examples of convolution now, especially for 2 D data • Consists of filtering an image A using a filter (mask, template) B. • Mask is a small image whose pixel values are called weights. • Weights modify relationships between pixels.

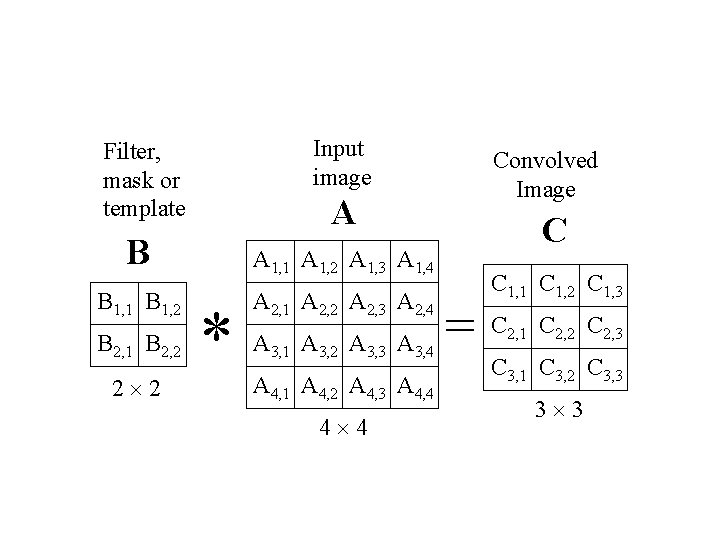
Input image Filter, mask or template A B B 1, 1 B 1, 2 B 2, 1 B 2, 2 2 2 A 1, 1 A 1, 2 A 1, 3 A 1, 4 A 2, 1 A 2, 2 A 2, 3 A 2, 4 A 3, 1 A 3, 2 A 3, 3 A 3, 4 A 4, 1 A 4, 2 A 4, 3 A 4, 4 4 4 Convolved Image C C 1, 1 C 1, 2 C 1, 3 =C 2, 1 C 2, 2 C 2, 3 C 3, 1 C 3, 2 C 3, 3 3 3

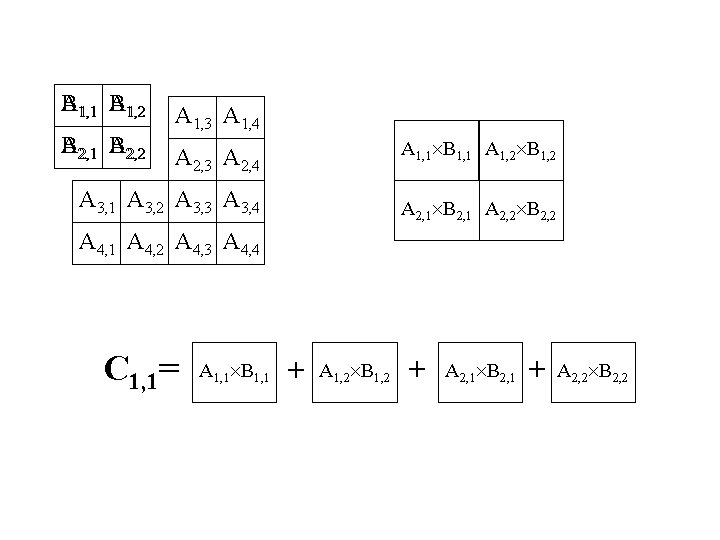
A A 1, 2 B 1, 1 B A B 2, 1 B A 2, 2 A 1, 3 A 1, 4 A 2, 3 A 2, 4 A 1, 1 B 1, 1 A 1, 2 B 1, 2 A 3, 1 A 3, 2 A 3, 3 A 3, 4 A 2, 1 B 2, 1 A 2, 2 B 2, 2 A 4, 1 A 4, 2 A 4, 3 A 4, 4 C 1, 1= A 1, 1 B 1, 1 A 1, 2 B 1, 2 A 2, 1 B 2, 1 A 2, 2 B 2, 2

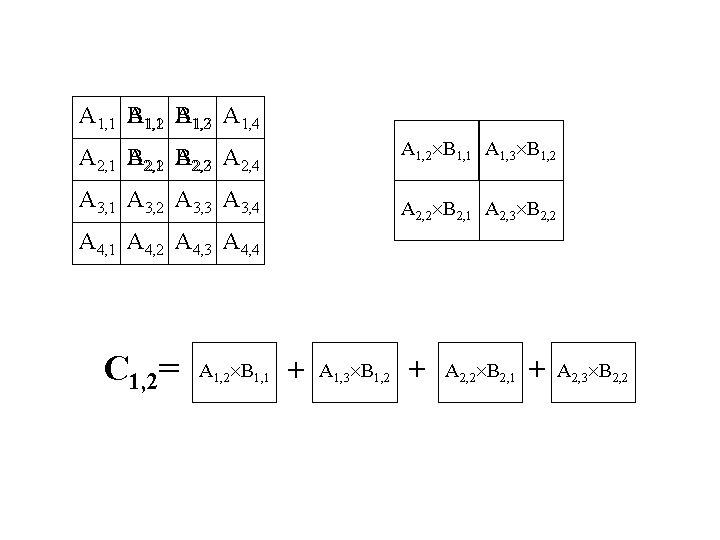
A 1, 1 B 1, 2 A 1, 3 A 1, 4 A 2, 1 B 2, 2 A 2, 3 A 2, 4 A 1, 2 B 1, 1 A 1, 3 B 1, 2 A 3, 1 A 3, 2 A 3, 3 A 3, 4 A 2, 2 B 2, 1 A 2, 3 B 2, 2 A 4, 1 A 4, 2 A 4, 3 A 4, 4 C 1, 2= A 1, 2 B 1, 1 A 1, 3 B 1, 2 A 2, 2 B 2, 1 A 2, 3 B 2, 2

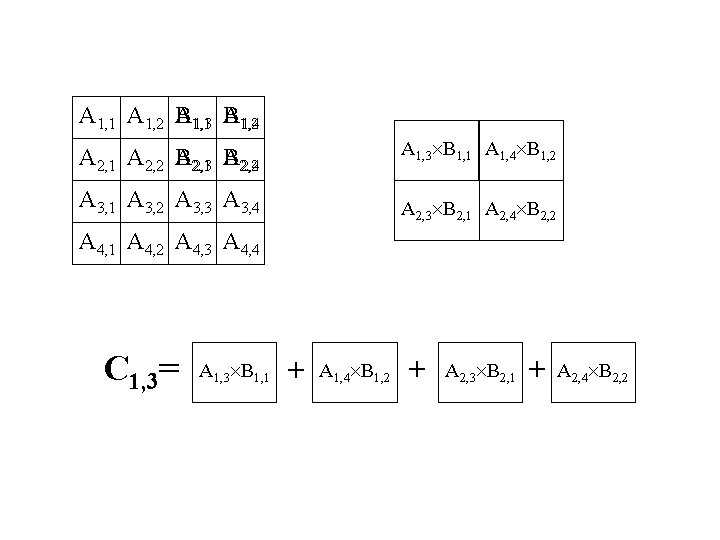
A 1, 1 A 1, 2 A B 1, 1 A 1, 2 1, 3 B 1, 4 A 2, 1 A 2, 2 A B 2, 1 A 2, 2 2, 3 B 2, 4 A 1, 3 B 1, 1 A 1, 4 B 1, 2 A 3, 1 A 3, 2 A 3, 3 A 3, 4 A 2, 3 B 2, 1 A 2, 4 B 2, 2 A 4, 1 A 4, 2 A 4, 3 A 4, 4 C 1, 3= A 1, 3 B 1, 1 A 1, 4 B 1, 2 A 2, 3 B 2, 1 A 2, 4 B 2, 2

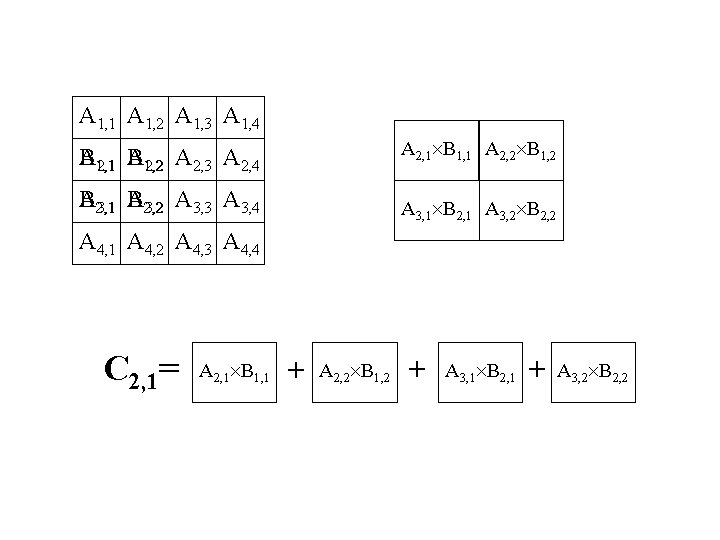
A 1, 1 A 1, 2 A 1, 3 A 1, 4 A B 1, 1 A 1, 2 2, 1 B 2, 2 A 2, 3 A 2, 4 A 2, 1 B 1, 1 A 2, 2 B 1, 2 A B 2, 1 A 2, 2 3, 1 B 3, 2 A 3, 3 A 3, 4 A 3, 1 B 2, 1 A 3, 2 B 2, 2 A 4, 1 A 4, 2 A 4, 3 A 4, 4 C 2, 1= A 2, 1 B 1, 1 A 2, 2 B 1, 2 A 3, 1 B 2, 1 A 3, 2 B 2, 2

A 1, 1 A 1, 2 B A 1, 1 A 1, 2 1, 3 B 1, 4 A 2, 1 A 2, 2 B A 1, 1 A 1, 2 2, 1 2, 3 B 2, 2 2, 4 A 3, 1 A 3, 2 B A 1, 1 A 1, 2 2, 1 3, 3 B 2, 2 3, 4 A 4, 1 A 4, 2 B A 2, 1 A 2, 2 4, 3 B 4, 4

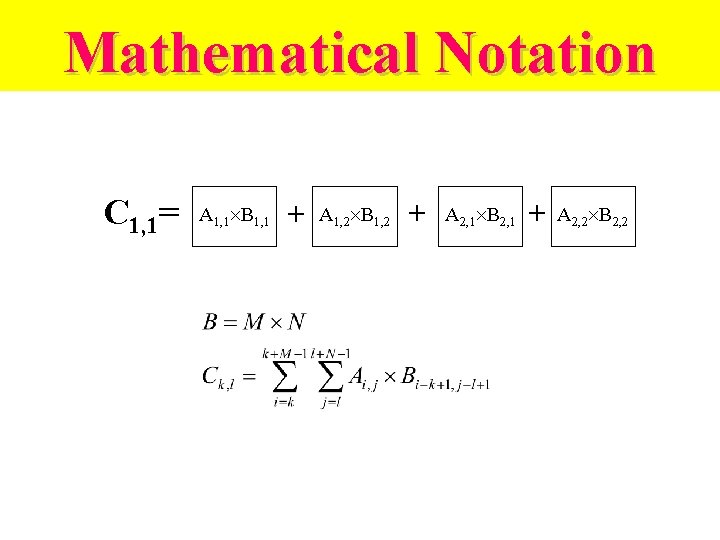
Mathematical Notation C 1, 1= A 1, 1 B 1, 1 A 1, 2 B 1, 2 A 2, 1 B 2, 1 A 2, 2 B 2, 2

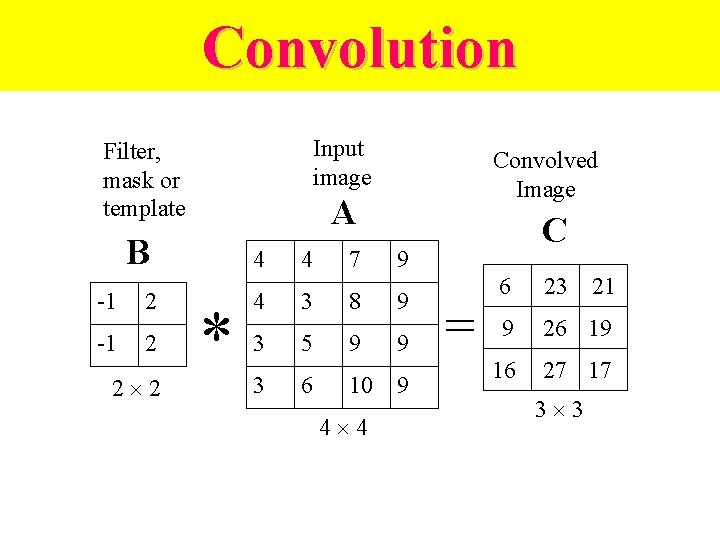
Convolution Input image Filter, mask or template A B -1 2 2 2 Convolved Image 4 4 7 9 4 3 8 9 3 5 9 9 3 6 10 4 4 C 9 = 21 6 23 9 26 19 16 27 17 3 3

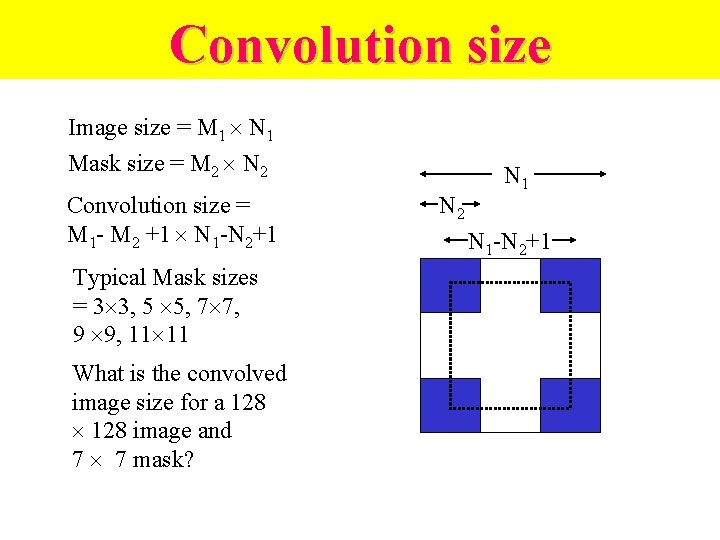
Convolution size Image size = M 1 N 1 Mask size = M 2 N 2 Convolution size = M 1 - M 2 +1 N 1 -N 2+1 Typical Mask sizes = 3 3, 5 5, 7 7, 9 9, 11 11 What is the convolved image size for a 128 image and 7 7 mask? N 2 N 1 -N 2+1

* 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 = We convolve with 9*9 averaging filter

Nonlinear Neighbourhood Operations • Maximum • Minimum • Median We discussed already sorter architecture (three variants – pipelined, butterfly combinational and sequential controller). It can be used for all these operations, and also for other non-linear operators

Max and Min Operations 61 621 59 1 65 62 59 57 1 63 1 60 56 60 63 59 55 58 57 49 53 55 45 63=max, 59=min C 1, 2= 59 63

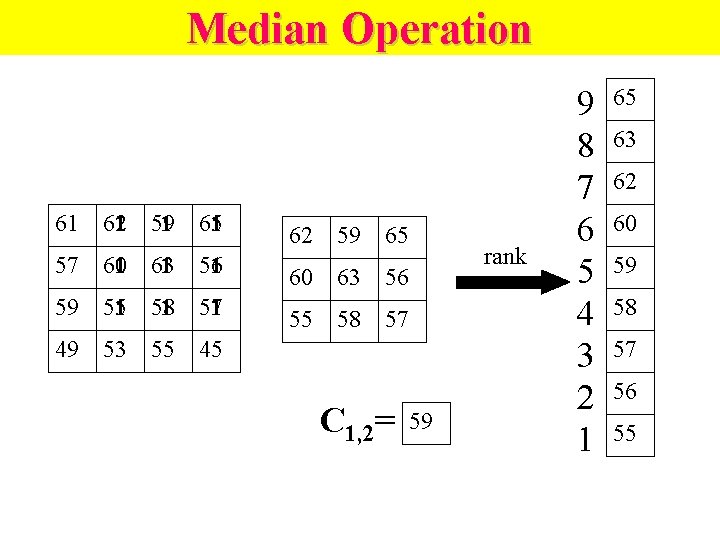
Median Operation 61 621 59 1 651 57 601 63 1 59 55 1 49 53 62 59 65 561 60 63 56 58 1 571 55 58 57 55 45 C 1, 2= rank 59 9 8 7 6 5 4 3 2 1 65 63 62 60 59 58 57 56 55

9 x 9 Median

Edge Detection • What do we mean by edge detection? • What is an edge?

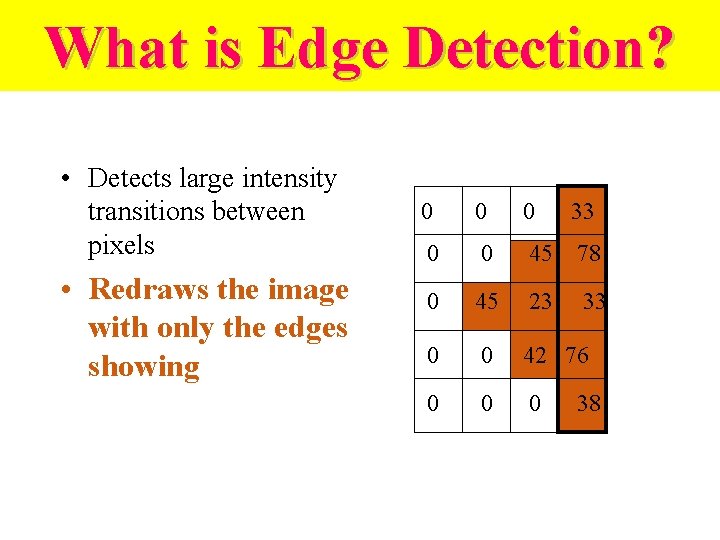
What is Edge Detection? • Detects large intensity transitions between pixels • Redraws the image with only the edges showing 0 0 0 33 0 0 45 78 0 45 23 33 0 0 42 76 0 0 0 38

What is an Edge? Edge easy to find

What is an Edge? Where is edge? Single pixel wide or multiple pixels?

What is an Edge? Noise is here Noise: have to distinguish noise from actual edge

What is an Edge? Is this one edge or two?

What is an Edge? Texture discontinuity

Edge Detection – so what is an edge to be detected? • What is an edge – A large change in image brightness of a short spatial distance – Edge strength = (I(x, y)-I(x+dx, y))/dx But this general definition still allows for many theories, software implementation and hardware architectures.

Now we will discuss and illustrate various kinds of filter operators

Edge Detection Filters • High - Pass Filtering Eliminates Uniform Regions (Low Frequencies) • edge “detection” or “enhancement”

Edge Detection Filters

Edge Filters Edge Detection Continued • Sum of Kernel Coefficients = 0 • differences in signs emphasize differences in pixel values • reduces average image intensity • Negative pixel values in output?

Edge Direction vertical horizontal diagonal

Directional High Pass Filters

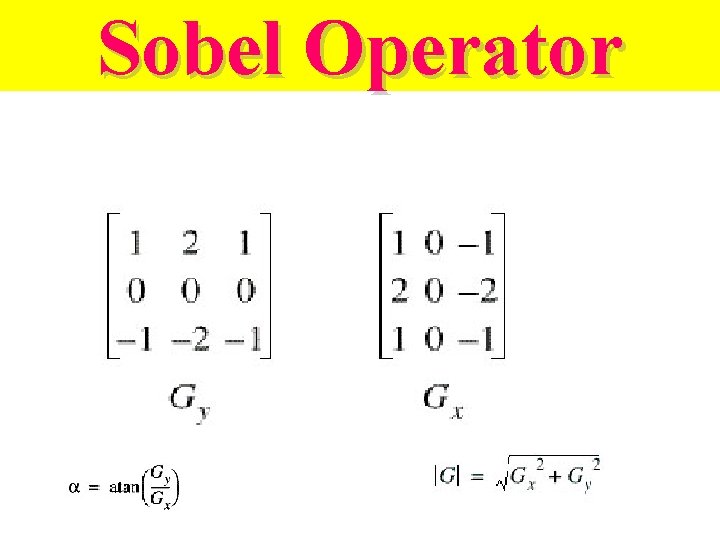
Convolution Edge Detection using Sobel and similar operators

Sobel Operator Example of Sobel Operator

Sobel Edge Detection

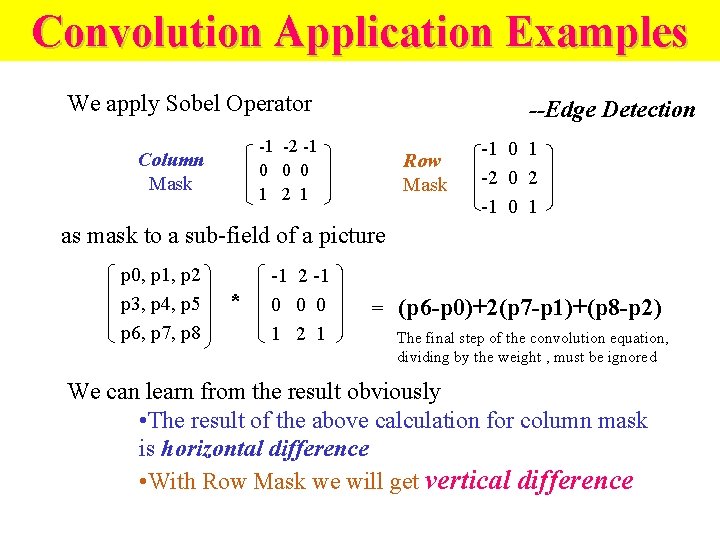
Convolution Application Examples We apply Sobel Operator --Edge Detection -1 -2 -1 0 0 0 1 2 1 Column Mask Row Mask -1 0 1 -2 0 2 -1 0 1 as mask to a sub-field of a picture p 0, p 1, p 2 p 3, p 4, p 5 p 6, p 7, p 8 * -1 2 -1 0 0 0 1 2 1 = (p 6 -p 0)+2(p 7 -p 1)+(p 8 -p 2) The final step of the convolution equation, dividing by the weight , must be ignored We can learn from the result obviously • The result of the above calculation for column mask is horizontal difference • With Row Mask we will get vertical difference

Convolution Application Examples --Edge Detection with Sobel Operator The weight of a mask determines the grey level of the image after convolution. Like the weight of Sobel Mask W W= (-1) + (-2) + (-1) + 0 + 0 +1 + 2 +1= 0 The resulting image lost its “lightness” to be dark.

Sobel Operator

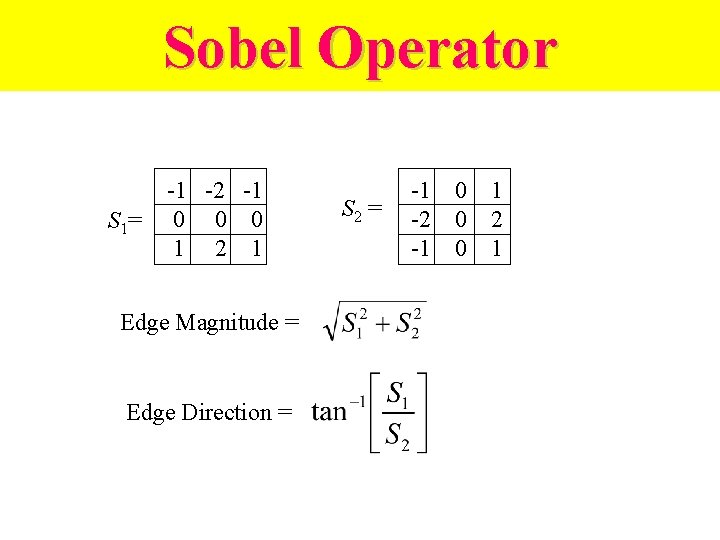
Sobel Operator S 1= -1 -2 -1 0 0 0 1 2 1 Edge Magnitude = Edge Direction = S 2 = -1 -2 -1 0 0 0 1 2 1

Comparison of Edge Detection Algorithms Canny Prewitt Ticbetts Sobel

Edge Direction Assymetric kernels detect edges from specific directions East North 1 1 -1 -1 -1 1 -2 -1 1 1 -1 1 -2 1 1

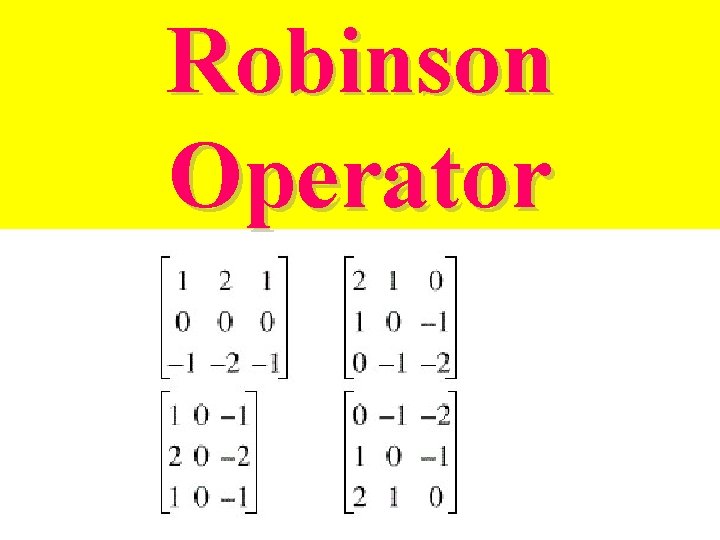
Robinson Operator

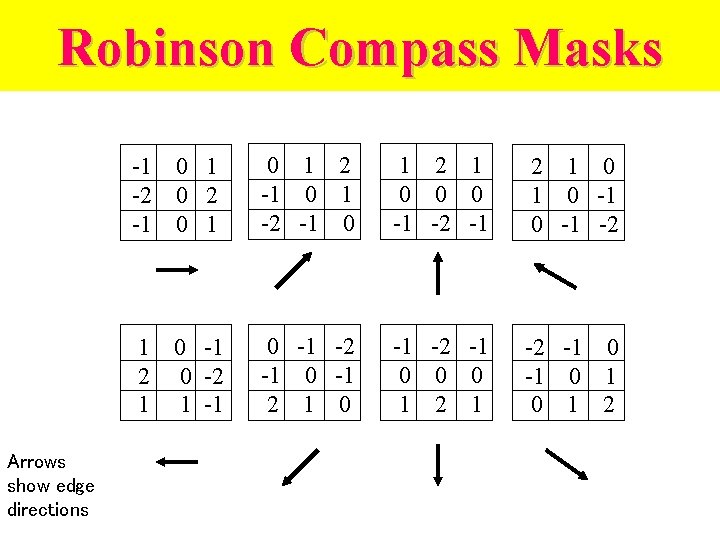
Robinson Compass Masks Arrows show edge directions -1 -2 -1 0 2 0 1 2 -1 0 1 -2 -1 0 1 2 1 0 0 0 -1 -2 -1 2 1 0 -1 -2 1 0 -1 0 -2 1 -1 0 -1 -2 -1 0 -1 2 1 0 -1 -2 -1 0 0 0 1 2 1 -2 -1 0 1 0 1 2

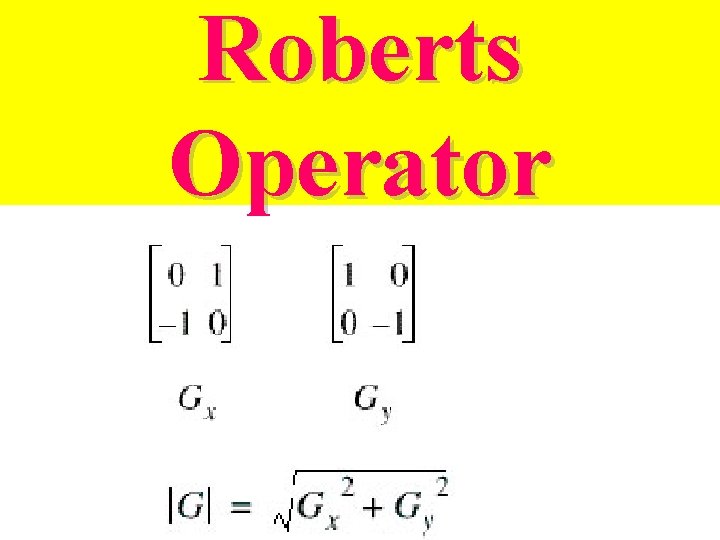
Roberts Operator

Roberts Operator or 1 0 0 -1 0 1 + -1 0 • Does not return any information about the orientation of the edge

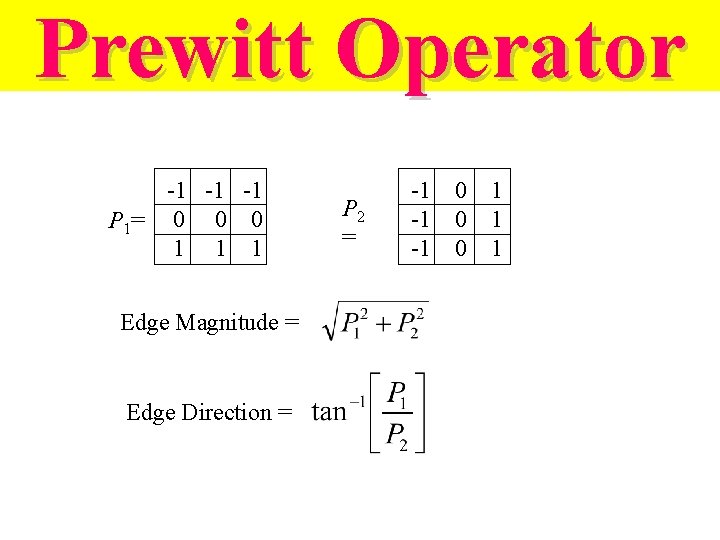
Prewitt Operator -1 -1 -1 P 1= 0 0 0 1 1 1 Edge Magnitude = Edge Direction = P 2 = -1 -1 -1 0 0 0 1 1 1

Edge Detection Filters Prewitt Row

0 1 2 -1 0 1 -2 -1 0 Original and filtered cow 1 2 1 0 0 0 -1 -2 -1

Edge Detection Filters: compare Edge Detection (continued) Prewitt and Sobel • First Order (Gradient) Kernels • Prewitt Row 1 0 -1 • Sobel Row 1 0 -1 2 0 -2 1 0 -1 • Combine Row and Column Operators

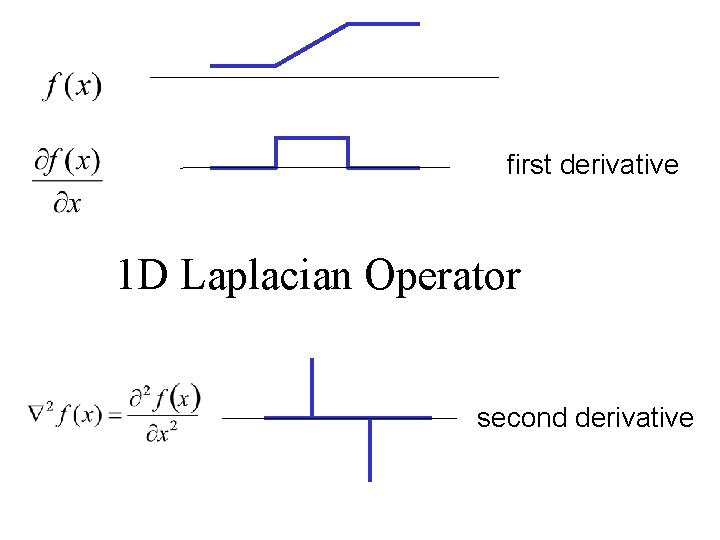
first derivative 1 D Laplacian Operator second derivative

2 D Laplacian Operator Convolution masks approximating a Laplacian 0 -1 4 -1 0 1 -2 4 -2 1 -1 -1 8 -1 -1 This is just one example of Laplacian, we can use much larger window

0 -1 4 -1 0 Input Mask Output

Image Processing Operations for Early Vision: Edge Detection

Reminder: Effect of Filters low high

Edges … are the important part of images simplest, least robust intensity color edges textures contours condensation. . . most difficult, most robust There are many letters B occluded by black shape here. How to find them?

Image Processing Operations Edge Detection • Edges are curves in the image plane across which there is a “significant” change in image brightness. • The goal of edge detection is the construction of an idealized line drawing

Pixels on edges

Edges found

Edge effects: rarely ideal edges Not all information is created equal. . .

Causes of edges • Depth discontinuity – One surface occludes another • Surface orientation discontinuity – the edge of a block • reflectance discontinuity – texture or color changes • illumination discontinuity – shadows

Edges: causes What are they? Why? four physical events that cause image edges. . .

Edges: causes What are they? Why? four physical events that cause image edges. . . discontinuities in • surface color/intensity • surface normal • depth • lighting (specularities)