Negating Nested Quantifiers Ixx has an internet connection
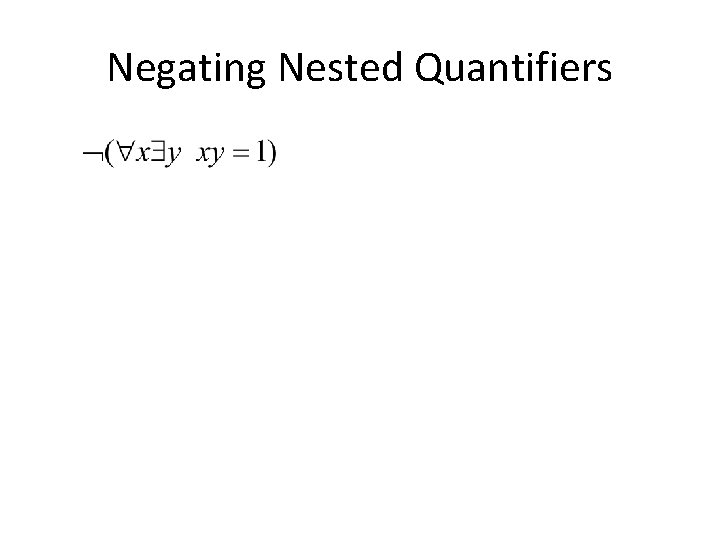




































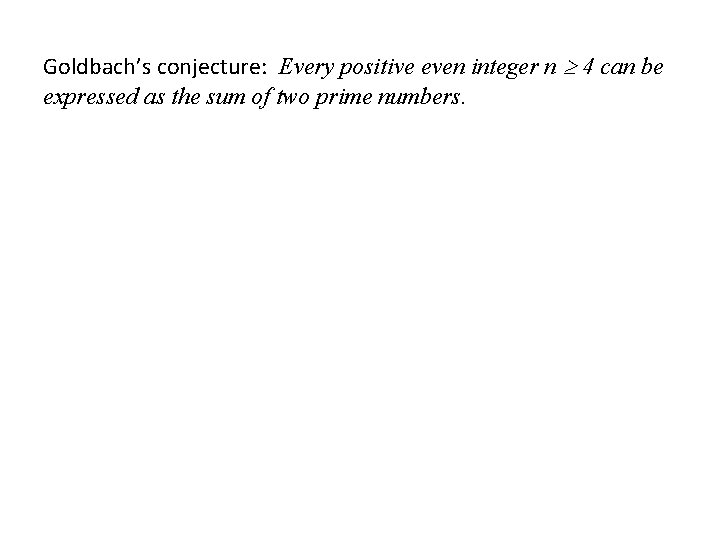
- Slides: 40
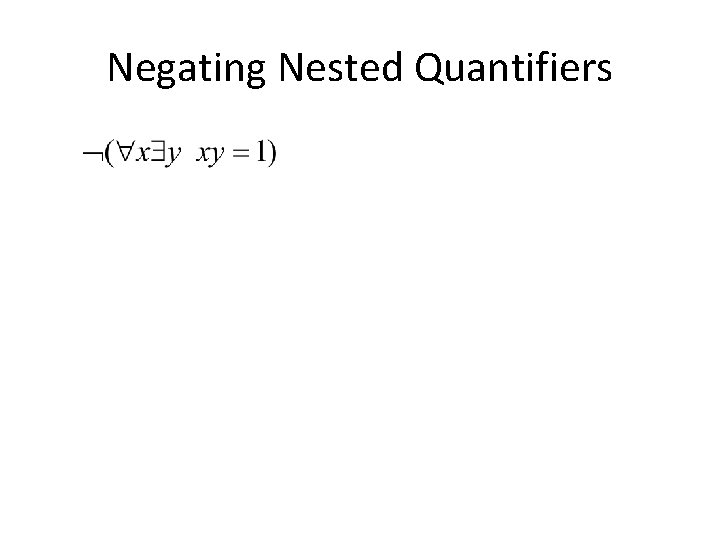
Negating Nested Quantifiers


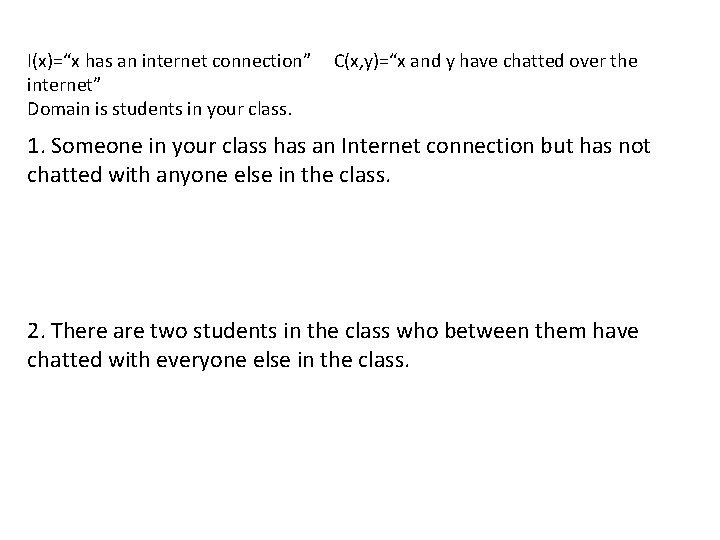
I(x)=“x has an internet connection” C(x, y)=“x and y have chatted over the internet” Domain is students in your class. 1. Someone in your class has an Internet connection but has not chatted with anyone else in the class. 2. There are two students in the class who between them have chatted with everyone else in the class.

Section 1. 5 – Rules of Inference • Terms: – Argument – Premises – Conclusion – Valid

Standard Rules of Inference (Each is based on a tautology) Modus Ponens Modus Tollens Hypothetical Syllogism

Standard Rules of Inference (Continued) Addition Simplification Conjunction

Standard Rules of Inference (Continued) Disjunctive Syllogism Resolution

Examples Alice is a mathematics major. Therefore, Alice is either a mathematics major or a computer science major. If it snows today, the university will close. The university is not closed today. Therefore, it did not snow today. If I go swimming, then I will stay in the sun too long. If I stay in the sun too long, then I will sunburn. Therefore, if I go swimming, then I will sunburn.

Example Use rules of inference to show that the hypotheses “Randy works hard, ” “If Randy works hard, then he is a dull boy” and “If Randy is a dull boy, then he will not get the job” imply the conclusion “Randy will not get the job. ”

Rules of Inference for Quantified Statements Universal Instantiation Universal Generalization

Rules of Inference for Quantified Statements (Continued) Existential Instantiation Existential Generalization

Combining Rules of Inference for Quantified Statements Universal Modus Ponens Universal Modus Tollens

Examples: Drawing Conclusions “Every computer science major has a personal computer. ” “Ralph does not have a personal computer. ” “Ann has a personal computer. ” “Joe is a computer science major. ”

Valid Arguments vs Fallacies • Valid arguments are constructed using… • A fallacy is a (so-called) argument which is not so constructed. – Affirming the conclusion – Denying the hypothesis – Begging the question p

Examples: Valid Argument or Fallacy? 1. All students in this class understand logic. Xavier is a student in this class. Therefore, Xavier understands logic. 2. Every computer science major takes discrete mathematics. Natasha is taking discrete mathematics. Therefore, Natasha is a computer science major.

3. All parrots like fruit. My pet bird is not a parrot. Therefore, my pet bird does not like fruit. 4. Everyone who eats granola every day is healthy. Linda is not healthy. Therefore, Linda does not eat granola every day.

Section 1. 6 – Introduction to Proofs Formal Proofs Definitions: Proof- Theorem. Proposition. Axiom or postulate-

Definitions Continued: Lemma- Corollary- Conjecture

Quantifiers • Remember that when no quantifier is given, a universal quantification is assumed. If xy > 0, then either x and y are both positive or x and y are both negative


Direct proof: Assume p is true. Show by a direct argument that q is true. Task: Prove the statement: “If a person likes math then he/she is cool. ” Proof:


Indirect proof: Assume q is false. Show by a direct argument that p is false. Task: Prove the statement: “If a person likes math then he/she is cool. ” Proof:


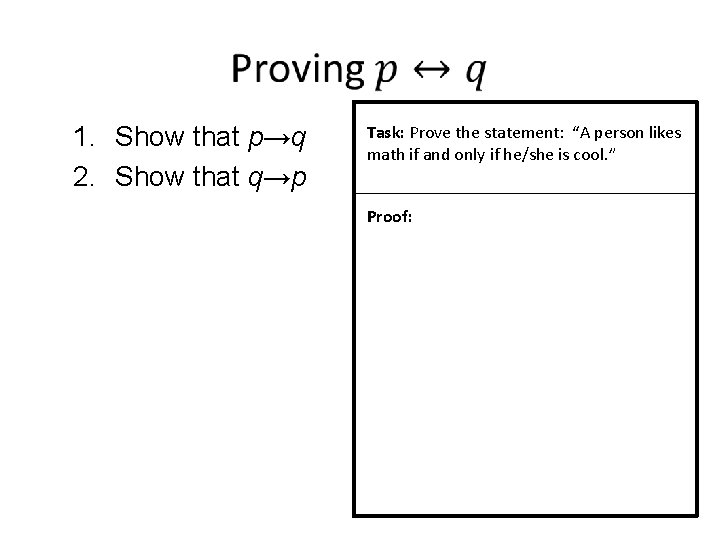
1. Show that p→q 2. Show that q→p Task: Prove the statement: “A person likes math if and only if he/she is cool. ” Proof:

Proving Multiple Statements Equivalent

Prove these statements are equivalent, where a and b are real numbers: (i) a is less than b, (ii) the average of a and b is greater than a, and (iii) the average of a and b is less than b.


Other Types of Proof • Vacuous proof • Trivial proof • Proof by contradiction

Prove that the product of a non-zero rational numbers and an irrational number is irrational using proof by contradiction.

Mistakes in Proofs

Section 1. 7 – Proof Methods and Strategy • Proof by cases • Exhaustive Proof



Theorems and Quantifiers • Existence proofs (constructive vs. nonconstructive) Constructive: Show that there is a positive integer that can be written as the sum of cubes of positive integers in two different ways.


Uniqueness quantifier and uniqueness proofs

Counter-Examples •

Open Problems •
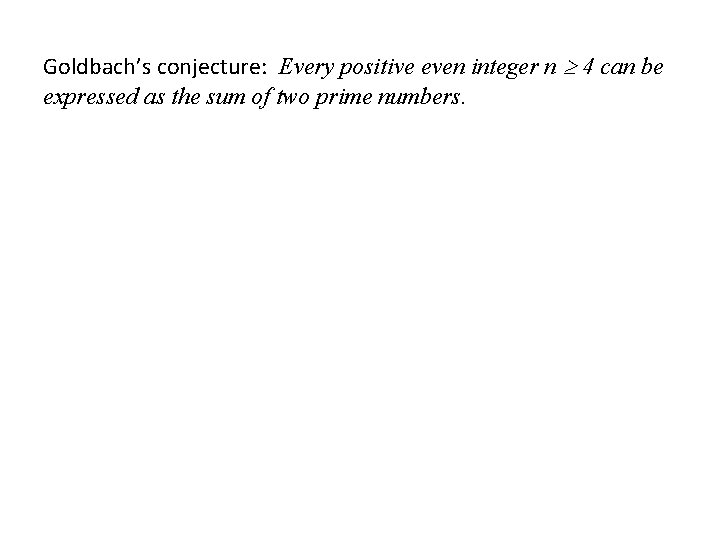
Goldbach’s conjecture: Every positive even integer n 4 can be expressed as the sum of two prime numbers.