NEARLY OPTIMAL SEPARATIONS BETWEEN COMMUNICATION OR QUERY COMPLEXITY

NEARLY OPTIMAL SEPARATIONS BETWEEN COMMUNICATION (OR QUERY) COMPLEXITY AND PARTITIONS Andris Ambainis (Latvia), Martins Kokainis (Latvia), Robin Kothari (MIT)

COMMUNICATION COMPLEXITY • Alice holds x X, Bob holds y Y. • Dcc(f) - minimum amount of communication to compute F(x, y).

COMMUNICATION COMPLEXITY • k bit protocol 2 k possible transcripts. • Transcript = rectangle Xi Yi, Xi, Yi – sets of inputs for Alice and Bob. k bit protocol partition of X Y into 2 k rectangles, F constant on each rectangle

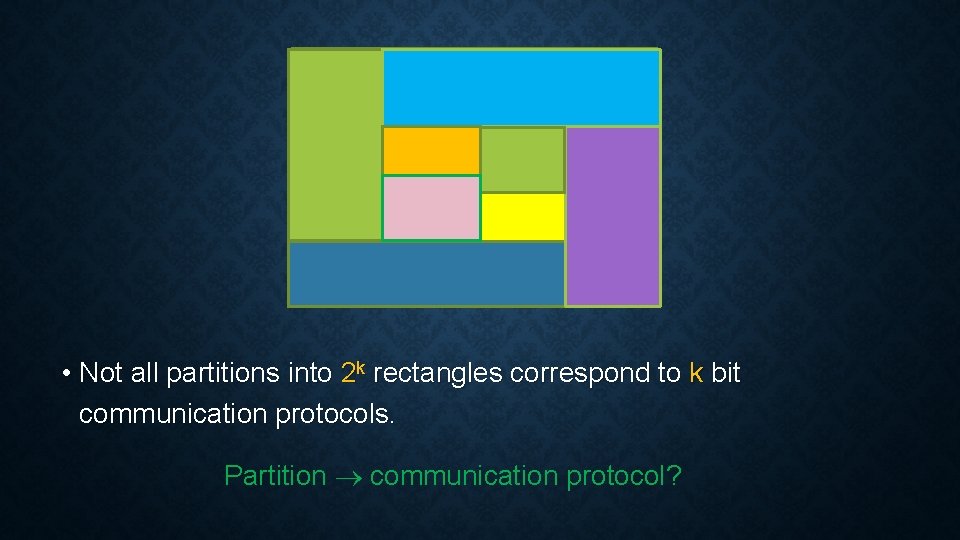
• Not all partitions into 2 k rectangles correspond to k bit communication protocols. Partition communication protocol?

COMMUNICATION VS. PARTITION NUMBER • (F) – min number of rectangles Xi Yi in a partition with F constant on every rectangle. • Dcc(F) log (F) [Yao, 1979]. • Dcc(F) = O(log 2 (F)) [Aho, Ullman, Yannakakis, 1983]. F: Dcc(F) 2 log (F) [Kushilevitz, Linial, Ostrovsky, 1999] F: Dcc(F) = (log 1. 5 (F)) [Goos, Pitassi, Watson, 2015]

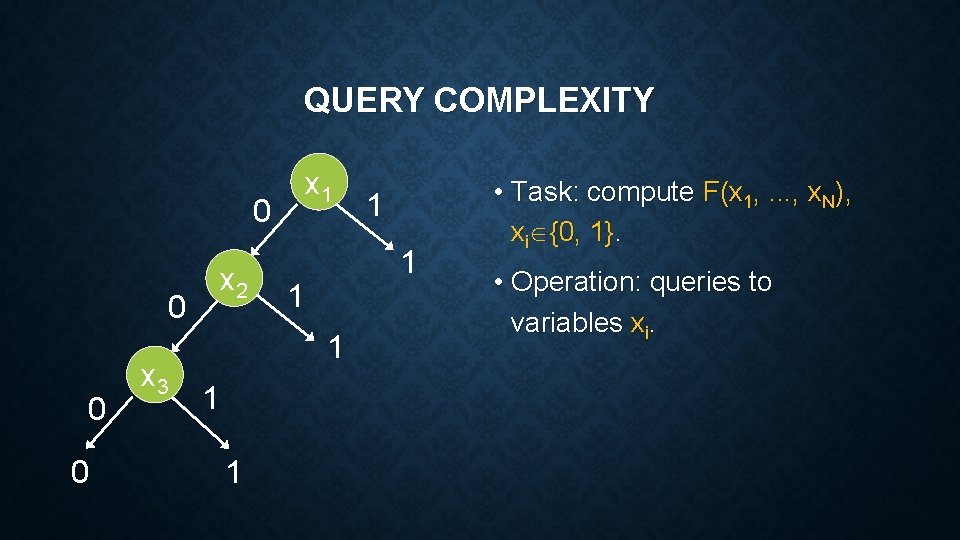
QUERY COMPLEXITY x 1 0 x 2 0 0 0 x 3 1 1 1 • Task: compute F(x 1, . . . , x. N), xi {0, 1}. • Operation: queries to variables xi.

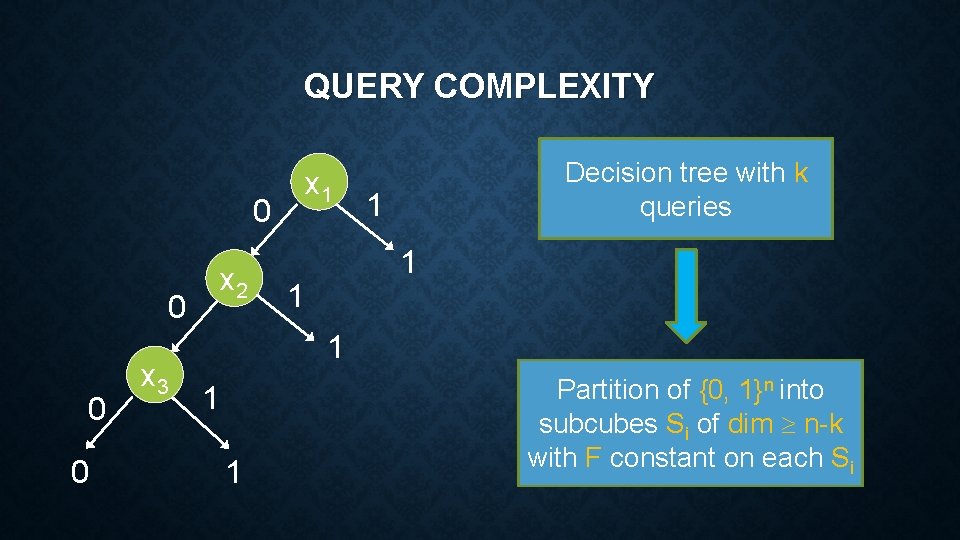
QUERY COMPLEXITY x 1 0 x 2 0 0 0 x 3 Decision tree with k queries 1 1 1 Partition of {0, 1}n into subcubes Si of dim n-k with F constant on each Si

QUERIES VS. PARTITIONS • D(F) – deterministic query complexity; • UC(F) – smallest k with a partition of {0, 1}n into subcubes defined by fixing k bits. • k D(F) k 2; F: D (F) = (UC 1. 5(F)) [Goos, Pitassi, Watson, 2015]

OUR SEPARATIONS •

CERTIFICATES • Certificate = partial assignment C such that: • x 1. . . xn satisfies C F(x 1. . . xn)=a. • OR(x 1, x 2, . . . x. N): • 1 -certificates: 1***, *1**, . . . , ***1. • 0 -certificates: 0000.

SUBCUBES VS. CERTIFICATES • Certificate subcube consisting of all x 1. . . xn that satisfy C. • Partition of {0, 1}n into subcubes collection of certificates with each x 1. . . xn satisfying exactly one C. Unambiguous certificates.

NOTATION • UC(F) – smallest k such that there is an unambiguous collection of C covering {0, 1}n. • UCa(F) – smallest k such that there is an unambiguous collection of C covering x: F(x)=a. • C(F) – smallest k such that there is a collection of C covering {0, 1}n.

CHEAT-SHEETS • [Aaronson, Ben-David, Kothari, STOC’ 16]. • Show R(F) = (Q 2. 5 -o(1)(F)). • Number of other separations.

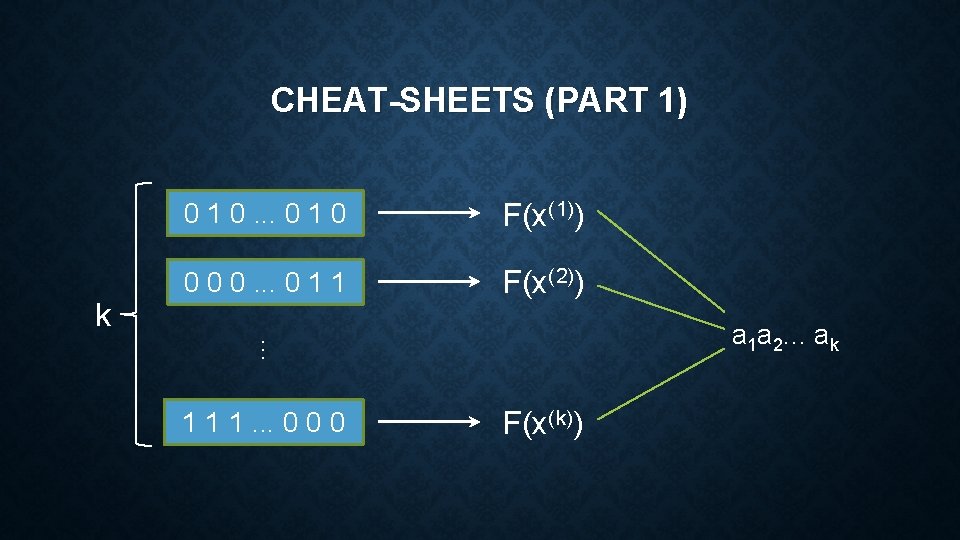
CHEAT-SHEETS (PART 1) k 0 1 0. . . 0 1 0 F(x(1)) 0 0 0. . . 0 1 1 F(x(2)) . . . a 1 a 2. . . ak 1 1 1. . . 0 0 0 F(x(k))

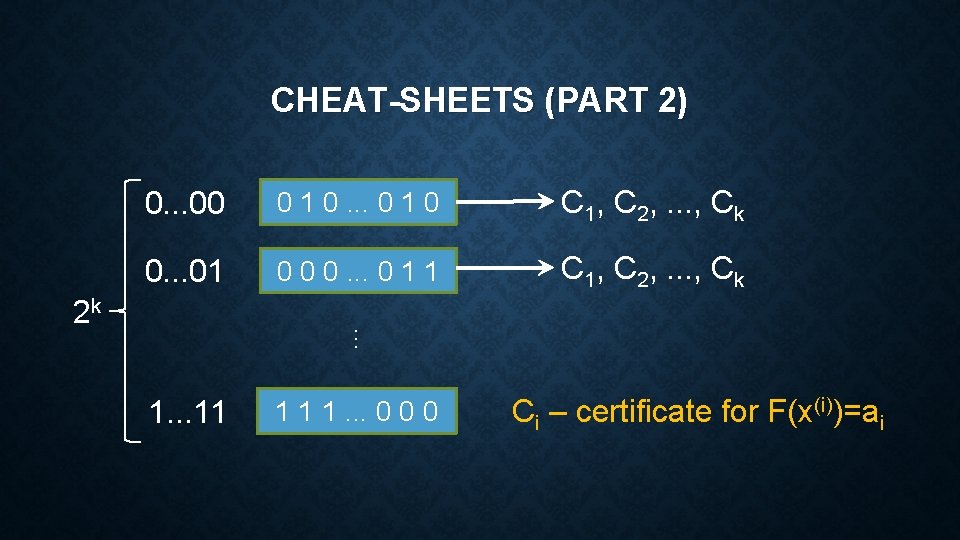
CHEAT-SHEETS (PART 2) 0. . . 00 0 1 0. . . 0 1 0 C 1, C 2, . . . , Ck 0. . . 01 0 0 0. . . 0 1 1 C 1, C 2, . . . , Ck 1. . . 11 1 1 1. . . 0 0 0 . . . 2 k Ci – certificate for F(x(i))=ai

CHEAT-SHEETS • Fcs=1 if: • F(x(1))=a 1, . . . , F(x(k))=ak; • Cheat-sheet a 1. . . ak contains descriptions of correct certificates for F(x(1))=a 1, . . . , F(x(k))=ak.

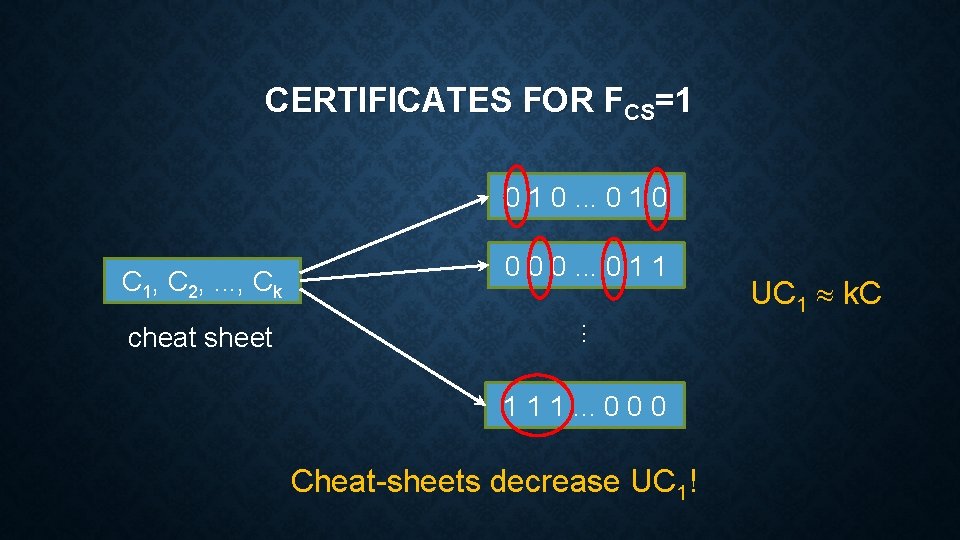
CERTIFICATES FOR FCS=1 0 1 0. . . 0 1 0 C 1, C 2, . . . , Ck . . . cheat sheet 0 0 0. . . 0 1 1 1. . . 0 0 0 Cheat-sheets decrease UC 1! UC 1 k. C

OTHER COMPLEXITY MEASURES • UC 1 (FCS) k C(F); • UC 0 (FCS) k UC(F); decreases does not decrease • C(FCS) k C(F); • D(FCS) k D(F); • Typically, k log N, can be omitted.

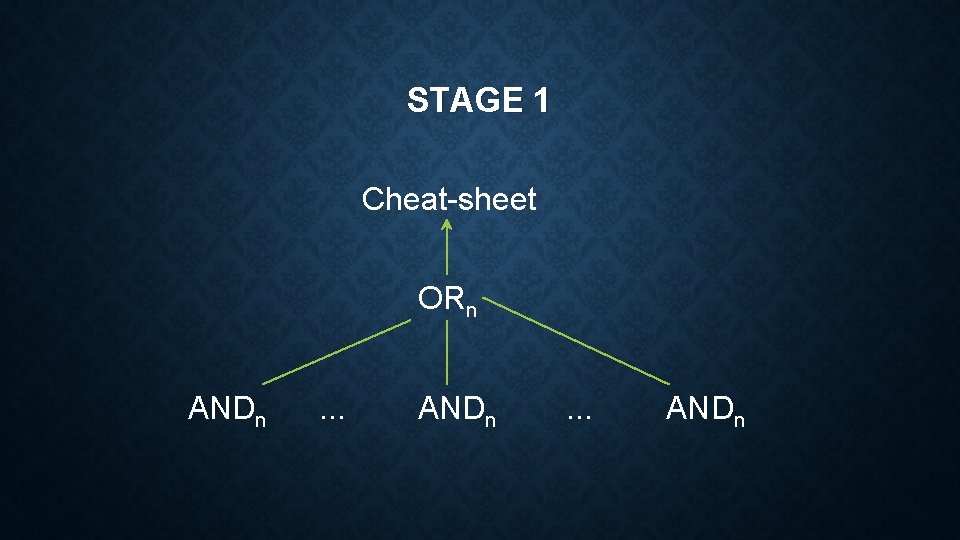
STAGE 1 Cheat-sheet ORn ANDn . . . ANDn

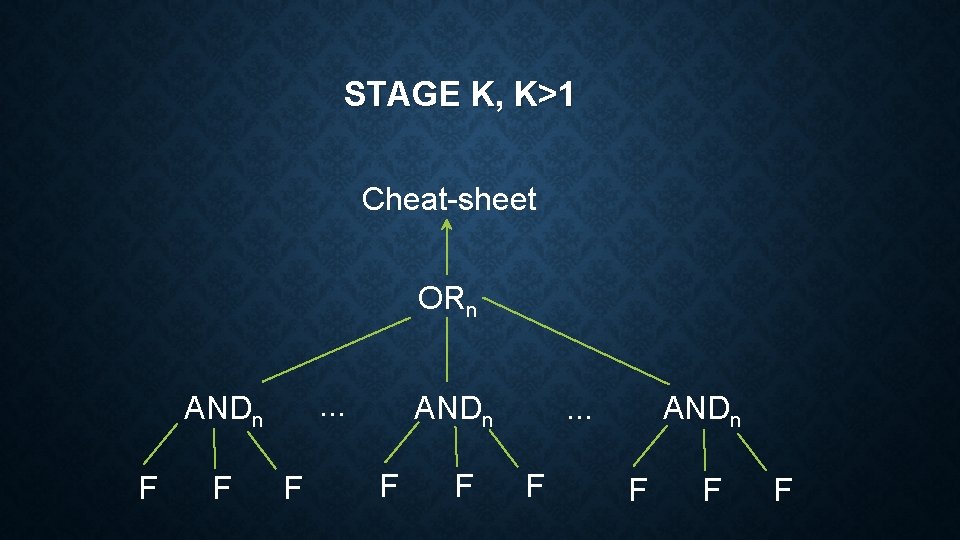
STAGE K, K>1 Cheat-sheet ORn. . . ANDn F F F ANDn F F . . . F ANDn F F F

D C 0 C 1 UC 0 UC 1 AND n 1 n n n OR n 2 n n n 2 n cheat-sheet

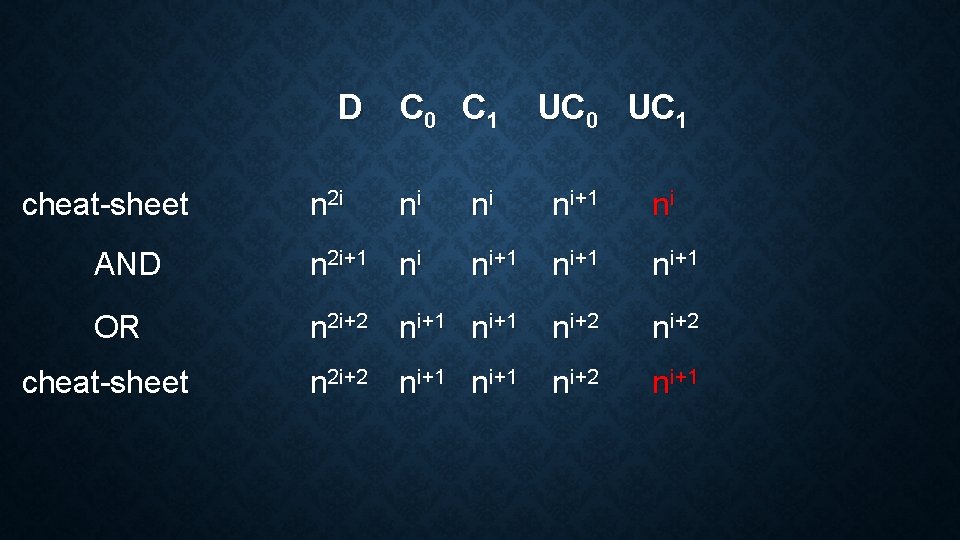
D cheat-sheet n 2 i C 0 C 1 ni UC 0 UC 1 ni ni+1 ni AND n 2 i+1 ni ni+1 OR n 2 i+2 ni+1 ni+2 ni+1 cheat-sheet

RESULT • D n 2 i, UC ni+1. • Theorem D(F) = (UC 2 -o(1)(F)). R(F) = (UC 2 -o(1)(F)) follows similarly.

QUANTUM RESULTS • Theorem Q(F)= (UC 1. 5 -o(1)(F)). • Theorem Q(F)= (UC 12 -o(1)(F)). • Cheat-sheet+OR+BKK (instead of AND).

CONCLUSION • Almost quadratic gap between partitions and deterministic communication/query complexity. • Simpler construction? • Gap for randomized communication vs. partitions? • Quantum?