Nearly Free Electron Model Prsentation fr Solid State

Nearly Free Electron Model Präsentation für Solid State Physics 0530982 Andreas Katzensteiner andreas. katzensteiner@student. tugraz. at 0530720 Roland Schmied rolsch@sbox. tugraz. at 1

Inhaltsverzeichnis w w w Modell des freien Elektronengases-Nachteile Verbesserungen des Modells Elektronen im periodischen Potential Blochfunktionen Wellenfunktionen und Aufenthaltswahrscheinlichkeit Energie-Impuls-Relation Betrachtung eines Grenzfalles Hereinklappen der höheren Brillouinzonen Aufspaltung der Energiewerte Energielücke als Folge der Gitterperiodizität Quellen 2

Modell des freien Elektronengases - Nachteile w I: Einelektronennäherung w II: keine Wechselwirkung zwischen Elektronen w III: Kastenpotential w IV: Energieniveau kontinuierlich 3

Verbesserungen des Modells w Ersatz des Kastenpotentials durch periodisches Potential der Atomrümpfe w Festkörper unendlich ausgedehnt w Abweichungen von der Periodizität und von Oberflächeneffekten werden vernachlässigt 4

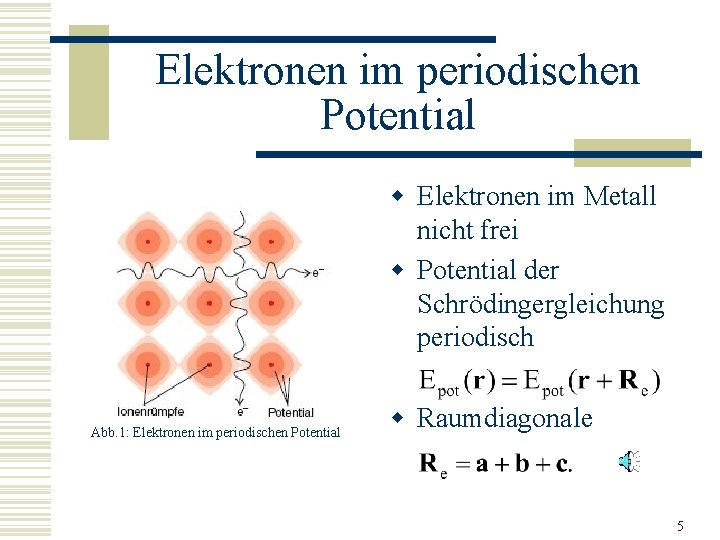
Elektronen im periodischen Potential w Elektronen im Metall nicht frei w Potential der Schrödingergleichung periodisch Abb. 1: Elektronen im periodischen Potential w Raumdiagonale 5

Blochfunktionen w Ansatz für Lösungsfunktion w Blochfunktionen w Energie des periodischen Potentials 6

Wellenfunktionen und Aufenthaltswahrscheinlichkeit w Überlagerung von einfallender und reflektierter Welle durch Braggreflexion an den Gitterebenen Abb. 2: stehende Welle an den Gitterebenen w Amplituden A und B gleich 7

Wellenfunktionen und Aufenthaltswahrscheinlichkeit w Aufenthaltswahrscheinlichkeitsdichten für ein Elektron Abb. 3: Aufenthaltswahrscheinlichkeitsdichten für ein Elektron 8

Energie-Impuls-Relation w Beschränkung der Energie-Impuls. Relation auf den Bereich: w Für Elektronenwellenfunktionen gilt: 9

Betrachtung eines Grenzfalles w gitterperiodische Potentialpot. E (r) konstant w Nur diskrete k-Werte erlaubt w Dispersionskurve eines freien Teilchens Abb. 4: Dispersionskurve eines freien Teilchens 10

Hereinklappen der höheren Brillouinzonen w Hereinklappen der höheren Brillouinzonen und Reduzierung der k-Werte auf erste Brillouinzone w Eigenfunktionen genügen den Bedingungen für Blochfunktionen 11

Aufspaltung der Energiewerte w Störung des Elektrons durch periodisches Potential der Atomrümpfe: w Linearkombination der gestörten Wellenfunktion w Näherungsweise Vereinfachung der Lösungen zu: w Ausbildung einer Energielücke 12

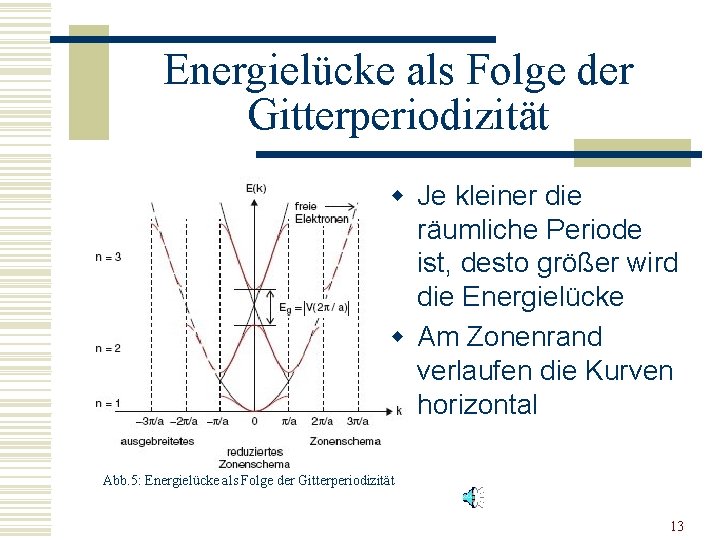
Energielücke als Folge der Gitterperiodizität w Je kleiner die räumliche Periode ist, desto größer wird die Energielücke w Am Zonenrand verlaufen die Kurven horizontal Abb. 5: Energielücke als Folge der Gitterperiodizität 13

Quellen w Festkörperphysik, Ibach u. Lüth, Springer-Verlag, 4. Auflage, Kapitel 7 w Introduction to Solid State Physics, Charles Kittel, was weiß ich was das für ein Verlag ist, 7. Auflage, Kapitel xy w Experimentalphysik 3, Wolfgang Demtröder, Springer-Verlag, 3. Auflage, Kapitel 13 14