nd 2 7 1 Binary Relations pass and

nd (2 § 7. 1 Binary Relations pass) and § 7. 2 n-ary Relations Longin Jan Latecki Slides adapted from Kees van Deemter who adopted them from Michael P. Frank’s Course Based on the Text Discrete Mathematics & Its Applications (5 th Edition) by Kenneth H. Rosen 10/16/2021 1

§ 7. 1 Binary Relations nd (2 pass) • Let A, B be any sets. A binary relation R from A to B is a subset of A×B. – E. g. , < can be seen as {(n, m) | n < m} • (a, b) R means that a is related to b (by R) • Also written as a. Rb; also R(a, b) – E. g. , a<b and < (a, b) both mean (a, b) < • A binary relation R corresponds to a characteristic function PR: A×B→{T, F} 10/16/2021 2

Complementary Relations • Let R: A, B be any binary relation. • Then, R: A×B, the complement of R, is the binary relation defined by R: ≡{(a, b) A×B | (a, b) R}=(A×B) − R} • Note this is just R if the universe of discourse is U = A×B; thus the name complement. • Note the complement of R is R. Example: < = {(a, b) | (a, b) <} = {(a, b) | ¬a<b} = ≥ 10/16/2021 3

Inverse Relations • Any binary relation R: A×B has an inverse relation R− 1: B×A, defined by R− 1 : ≡ {(b, a) | (a, b) R}. E. g. , <− 1 = {(b, a) | a<b} = {(b, a) | b>a} = >. • E. g. , if R: People x Foods is defined by a R b a eats b, then: b R− 1 a b is eaten by a. (Passive voice. ) 10/16/2021 4

Relations on a Set • A (binary) relation from a set A to itself is called a relation on the set A. • E. g. , the “<” relation from earlier was defined as a relation on the set N of natural numbers. 10/16/2021 5

Reflexivity and relatives • A relation R on A is reflexive iff a A(a. Ra). – E. g. , the relation ≥ : ≡ {(a, b) | a≥b} is reflexive. • R is irreflexive iff a A( a. Ra) • Note “irreflexive” does NOT mean “not reflexive”, which is just a A(a. Ra). 10/16/2021 6

Reflexivity and relatives • Theorem: A relation R is irreflexive iff its complementary relation R is reflexive. – Example: < is irreflexive; ≥ is reflexive. – Proof: trivial 10/16/2021 7

• Can you think of – Reflexive relations – Irreflexive relations Involving numbers, propositions or sets? 10/16/2021 8

Some examples • Reflexive: =, `have same cardinality’, <=, >=, , , etc. • Irreflexive: <, >, `have different cardinality’, 10/16/2021 9

Symmetry & relatives • A binary relation R on A is symmetric iff a, b((a, b) R ↔ (b, a) R). – E. g. , = (equality) is symmetric. < is not. – “is married to” is symmetric, “likes” is not. • A binary relation R is asymmetric if a, b((a, b) R → (b, a) R). – Examples: < is asymmetric, “likes” is not. 10/16/2021 10

Some direct consequences Theorems: 1. R is symmetric iff R = R− 1, 2. R is asymmetric iff R R− 1 is empty. 10/16/2021 11

Symmetry & relatives 1. R is symmetric iff R = R− 1 Suppose R is symmetric. Then (x, y) R (y, x) R (x, y) R− 1 Suppose R = R− 1 Then (x, y) R− 1 (y, x) R 10/16/2021 12

Symmetry & relatives 2. R is asymmetric iff R R− 1 is empty. (Straightforward application of the definitions of asymmetry and R− 1) 10/16/2021 13

Antisymmetry • Consider the relation x y – It is not symmetric. (For instance, 5 6 but not 6 5) – It is not asymmetric. (For instance, 5 5) – You might say it’s nearly symmetric, since the only symmetries occur when x=y • This is called antisymmetry: 10/16/2021 14

Antisymmetry • A binary relation R on A is antisymmetric iff a, b((a, b) R (b, a) R a=b). • Examples: , , 10/16/2021 15

Transitivity • A relation R is transitive iff (for all a, b, c) ((a, b) R (b, c) R) → (a, c) R. Example: “is an ancestor of” is transitive. 10/16/2021 16

Composite Relations • Let R: A×B, and S: B×C. Then the composite S R of R and S is defined as: S R = {(a, c) | b: a. Rb b. Sc} • Function composition is an example: writing f. T for the function-version of the relation T, we have S R(a, c) iff b: a. Rb b. Sc iff f. R(a)=b and f. S(b)=c iff f. S f. R(a)=c 10/16/2021 17
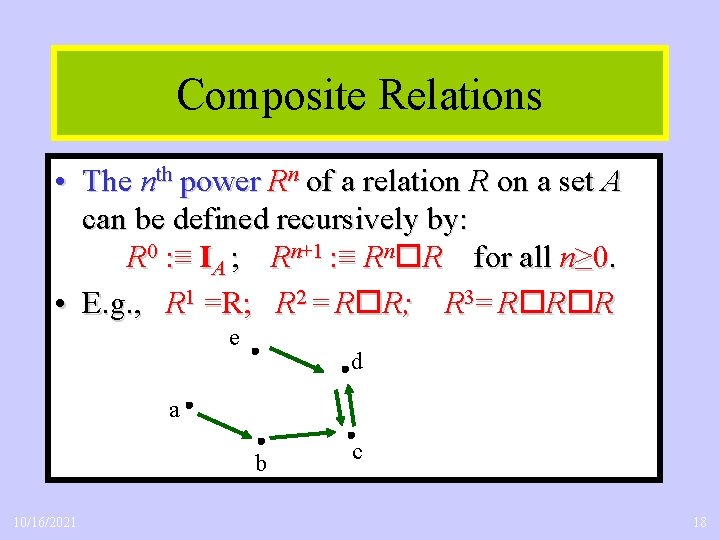
Composite Relations • The nth power Rn of a relation R on a set A can be defined recursively by: R 0 : ≡ IA ; Rn+1 : ≡ Rn R for all n≥ 0. • E. g. , R 1 =R; R 2 = R R; R 3= R R R e d a b 10/16/2021 c 18
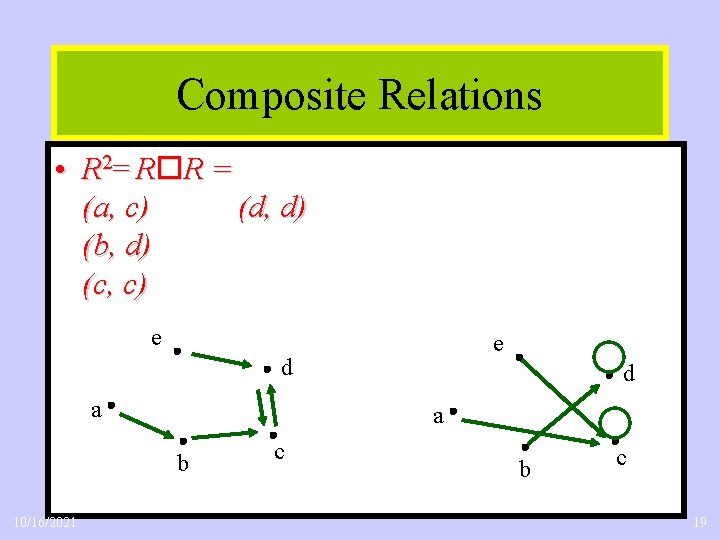
Composite Relations • R 2= R R = (a, c) (d, d) (b, d) (c, c) e e d a a b 10/16/2021 d c b c 19

§ 7. 2: n-ary Relations • An n-ary relation R on sets A 1, …, An, is a subset R A 1× … × An. • The sets Ai are called the domains of R. • The degree of R is n. • R is functional in the domain Ai if it contains at most one n-tuple (…, ai , …) for any value ai within domain Ai. 10/16/2021 20

§ 7. 2: n-ary Relations • An n-ary relation R on sets A 1, …, An, is a subset R A 1× … × An. • This is a straightforward generalisation of a binary relation. For example: • 3 -ary relations: – a is between b and c; – a gave b to c 10/16/2021 21

Relational Databases • A relational database is essentially just a set of relations. • A domain Ai is a primary key for the database if the relation R is functional in Ai. • A composite key for the database is a set of domains {Ai, Aj, …} such that R contains at most 1 n-tuple (…, ai, …, aj, …) for each composite value (ai, aj, …) Ai×Aj×… 10/16/2021 22

Selection Operators • Let A be any n-ary domain A=A 1×…×An, and let C: A→{T, F} be any condition (predicate) on elements (n-tuples) of A. • Then, the selection operator s. C is the operator that maps any (n-ary) relation R on A to the n-ary relation consisting of all n-tuples from R that satisfy C. That is, s. C(R) = {a R | C(a) = T} 10/16/2021 23

Selection Operator Example • Suppose we have a domain A = Student. Name × Standing × Soc. Sec. Nos • Suppose we define a condition Upperlevel on A: Upper. Level(name, standing, ssn) : ≡ [(standing = junior) (standing = senior)] • Then, s. Upper. Level is the selection operator that takes any relation R on A (database of students) and produces a relation consisting of just the upperlevel students (juniors and seniors). 10/16/2021 24

Projection Operators • Let A = A 1×…×An be any n-ary domain, and let {ik}=(i 1, …, im) be a sequence of indices all falling in the range 1 to n, – That is, 1 ≤ ik ≤ n for all 1 ≤ k ≤ m. • Then the projection operator on n-tuples is defined by: 10/16/2021 25

Projection Example • Suppose we have a ternary (3 -ary) domain Cars=Model×Year×Color. (note n=3). • Consider the index sequence {ik}= 1, 3. (m=2) • Then the projection P{i }maps each tuple k (a 1, a 2, a 3) = (model, year, color) to its image: • This operator can be usefully applied to a whole relation R Cars (a database of cars) to obtain a list of the model/color combinations available. 10/16/2021 26

Join Operator • Puts two relations together to form a combined relation. • If the tuple (A, B) appears in R 1, and the tuple (B, C) appears in R 2, then the tuple (A, B, C) appears in the join J(R 1, R 2). – A, B, and C can also be sequences of elements. 10/16/2021 27

Join Example • Suppose R 1 is a teaching assignment table, relating Lecturers to Courses. • Suppose R 2 is a room assignment table relating Courses to Rooms, Times. • Then J(R 1, R 2) is like your class schedule, listing (lecturer, course, room, time). • (For precise definition, see Rosen, p. 486) 10/16/2021 28
- Slides: 28