Natural Language Processing Transparent Intensional Logic Marie Du

Natural Language Processing (Transparent Intensional Logic) Marie Duží http: //www. cs. vsb. cz/duzi/

Natural Language Processing n The most important applications of TIL logical system in NLP q q n Logical analysis of natural language Multi-agent systems; agent’s communication and reasoning The TIL-Script functional programming language Materials to study: n http: //www. cs. vsb. cz/duzi/TIL. html n Duží M. , Jespersen B. , Materna P. (2010): Procedural Semantics for Hyperintensional Logic. Springer Duží M. , Materna P. (2012): TIL jako procedurální logika. n (Průvodce zvídavého čtenáře Transparentní intensionální logikou). Aleph Bratislava. http: //www. cs. vsb. cz/duzi/aleph. pdf

Logical semantics n Logic is q q q n about reasoning, about argumentation that is going from premises to a conclusion the analysis and appraisal of arguments When you do logic, you try to clarify reasoning and separate good from bad reasoning, i. e. , Separate valid arguments from invalid ones Valid argument (example) If you overslept, you are late You are not late You didn’t oversleep q The conclusion is logically entailed by the premises

Valid arguments An argument is valid if it would be contradictory (impossible) to have the premises all true and conclusion false. n When you do reasoning, you use natural language n When you analyse arguments, you must analyse premises in a fine-grained way so that not to infer something that is not entailed by the premises. n Our goal: to build up an inference machine that neither over -infers ( paradoxes), nor under-infers ( lack of knowledge) n The more fine-grained the analysis of the meaning of premises is, the better inference machine can we build up

Logical semantics n Propositional logic q n Is very limited; semantics reduced to assigning T(rue), F(alse) to atomic propositions and composing these propositions by means of truthvalue functions (Boolean) algebra of truthvalues 1 st-order predicate logic (FOL) q q Limited analysis of the structure of atomic propositions – up to assigning properties and relations to individuals Apt for mathematics, cs problems with natural language

Coarse-grained analysis problems Some prime numbers are even 1. 2. 3. Some odd numbers are even Some students are lazy q Formalization in FOL: x [P(x) Q(x)] Questions: q (1) (2) (3) q q How come that the sentences (1), (2), (3) have the same analysis? is an analytically true sentence is an analytically false sentence is an empirical sentence, maybe true, maybe false How come that the formula x [P(x) Q(x)] has interpretations in which it is true and other interpretations in which it is false if it is the analysis of (1) or (2)? How does the translation of natural language sentences into the language of FOL contribute to understanding their meaning ?

Coarse-grained analysis 1. No bachelor is married 2. No bachelor is rich FOL: x [P(x) Q(x)] or x [P(x) Q(x)] Questions: q q How come that both the sentences have two analyses, and which of them is the ‘correct’ one? After all, (1) is analytically true (true at all state-of-affairs), while (2) is an empirical sentence, which might be true at some state-of-affairs and false in others

Coarse-grained analysis of premises Does it matter? n n If we could always validly derive conclusions that are entailed by the premises, the coarse-grained analysis would be OK Does the analysis in FOL make it possible to validly derive all consequences entailed by the premises? Unfortunately, it does not. Coarse-grained analysis of premises yields paradoxes inferring something that is not entailed by the premises (over-inferring) and not inferring something that is entailed (underinferring)

Paradoxes n n n Necessarily, 8 5 The number of planets = 8 –––––––––––––––– Necessarily, the number of planets 5 q q n n n ? ? ? Quine’s paradox Solution: Modal logic, introducing an operator □ It is ordered to deliver a letter If the letter is delivered, then it is delivered or burnt out –––––––––––––––––––––– ? ? ? It is ordered to deliver the letter or burn out q q Ross’s paradox Deontic logic, introducing an operator O Substitution of identicals is not allowed within the scope of operators opaque, intensional contexts It removes symptoms but does not cure the cause

Paradoxes n n n John believes that Prague has 1. 048. 576 citizens 1. 048. 576 = 100 000(16) ––––––––––––––––– ? ? ? John believes that Prague has 100 000(16) citizens q n n n Doxastic / Epistemic logics, introduce operators B, K John knows that 1+1=2 Sin( ) = 0 –––––––––––– ? ? ? John knows that Sin( ) = 0 q q Doxastic / Epistemic logics, introduce operators B(elieve) and K(now) The paradox of logical/mathematical omniscience

Paradoxes n n n John calculates 2 + 5 2+5=7 ––––––– ? ? ? John calculates 7 Oidipus seeks the murderer of his father Oidipus is the murderer of his father ––––––––––––– ? ? ? Oidipus seeks Oidipus q Attitude logics, …

Paradoxes n n n n The US President is the husband of Melania Hillary wanted to become the US president –––––––––––––––––––– Hillary wanted to become the husband of Melania Tom believes that the King of France is wise –––––––––––––––––––– ? ? ? The King of France exists Tom is seeking an abominable snowman (yeti) –––––––––––––––––––– Abominable snowman exists q Logic – magic ? ? ?

Extensional vs. intensional (opaque) context n n When is the context extensional? The context is extensional if the extensional rules like substitution of identiticals and existential generalization are valid And when are these rules valid? In an extensional context q n Hmmm We stir clear of this circle by q q Defining three kinds of context first, and then Defining universally valid rules of inference

Transparent Intensional Logic (TIL) n There is a spreading and still growing tree of particular logics q q n It has been growing bottom up Is it OK? Shouldn’t here be just one universal logic? Aren’t logical rules valid universally? TIL – universal logical framework q q „top down“ approach Logical rules are valid universally, only they have to be properly applied

Procedural semantics of TIL Expression Sense (procedure, construction) tion denotation Ontology of TIL: ramified hierarchy of types 15

TIL Ontology (types of order 1) (non-procedural objects) n n Basic types truth-values {T, F} ( ) universe of discourse {individuals} ( ) times or real numbers ( ) possible worlds ( ) Functional types ( 1… n) partial functions ( 1 … n) q PWS Intensions – entities of type (( ) ); 16

Functional approach; sets and n relations All the denoted objects are functions, possibly in an extreme case 0 -ary functions without arguments, i. e. atomic objects like individuals of type or numbers of type q n n How then do we model sets and relations(-in-extension)? By characteristic functions. Hence, a set of elements is an object of type ( ), Binary relation between - and -objects is an object of type ( ) Examples. q q q The set of prime numbers is an object of type ( ); in symbols Prime/( ) The set of solutions of the equation Sin(x) = 0, i. e. the set of multiples of is also an object of type ( ) The relation > defined on numbers is an object of type ( )

Possible worlds n n no sci-phi ! No multiple universes Universe of discourse: discourse the collection of bare individuals – abstract hangers (determined just by an ID) to hang particular traits and relations on Possible world: world chronology of maximal consistent distributions of these basic traits among individuals PWS-intensions / (( ) ); or for short

Examples of PWS-intensions n propositions of type (( ) ) or for short; q n properties of individuals of type ((( ) ) ) or ( ) for short; q n denoted by verbs like ‘to kick’, ‘to like’, … individual offices (or roles) of type ; q n denoted by nouns or adjectives like ‘(being a) student’, ‘round’, … binary relations-in-intension between individuals of type ( ) ; q n denoted by sentences like “Tom is a student” denoted by definite descriptions like ‘the Pope’, ‘the US president’, ‘Miss World 2019’, … Attributes of type ( ) ; q denoted by terms ‘temperature in …’, ‘president of …’, ‘the mayor of …’

Examples of extensions (no domain ) n n n Logical objects like truth-functions and quantifiers are extensional (conjunction), (disjunction) and (implication) are of type ( ), and (Boolean negation) of type ( ). Quantifiers , are type-theoretically polymorphic total functions of type ( ( )), for an arbitrary type , defined as follows. q q n The universal quantifier is a function that associates a class A of -elements with T if A contains all elements of the type , otherwise with F. The existential quantifier is a function that associates a class A of -elements with T if A is a non-empty class, otherwise with F. Mathematical objects like the function + of type ( ), trigonometric functions are objects of type ( ), relations between numbers like >, <, … are of type ( )

Constructions n n Variables x, y, p, w, t, … v-construct Trivialization 0 C constructs C (of any type) q q n a fixed pointer to C and the dereference of the pointer. In order to operate on C, C needs to be grabbed, or ‘called’, first. Trivialization is such a grabbing mechanism. Closure [ x 1…xn X] 1 n ( 1… n) n Composition [F X 1 … Xn] n Execution 1 X, Double Execution 2 X ( 1… n) 1 n 21

TIL: three kinds of context n Hyperintensional; Hyperintensional construction of the denoted function is an object of predication n Tom computes Sin( ) n Tom believes that the Pope is wise but does not believe that the Bishop of Rome is wise n Intensional; Intensional the denoted function itself is an object of predication n Sine is a periodic function n Tom wants to become the Pope n Extensional; Extensional value of the denoted function is an object of predication n Sin( ) = 0 n The Pope is wise.

Hyperintensional context of displayed constructions “Tom computes Cotg( )” n n n Tom/ ; Compute/( ? ) ; computing is an empirical relation(-in-intension) of an individual to what? It cannot be a relation to a number, because 1. 2. n n It makes no sense to compute a number without any arithmetic operation There is no such number here; Cotg is undefined at the number It is the relation of an individual to the very meaning procedure encoded by ‘Cotg( )’; Tom wants to execute the procedure of applying the function Cotangent to the number Cotg/( ); / ; [0 Cotg 0 ] ; 0[0 Cotg 0 ] ?

TIL Ontology (higher-order types) n Constructions of order 1 o o n n construct entities belonging to a type of order 1 / belong to 1 : type of order 2 Constructions of order 2 o ( 1) ( 2) construct entities belonging to a type of order 2 or 1 / belong to 2 : type of order 3 Constructions of order n ( n) o construct entities belonging to a type of order n 1 o / belong to n : type of order n + 1 Functional entities: ( 1… n) / belong to n (n: the highest of the types to which , 1, …, n belong) And so on, ad infinitum 24

explicit intensionalization and temporalization n constructions of possible-world intensions directly encoded in the logical syntax: w t […w…. t…] w ; t ; 0 Happy ( ) ; 0 Pope w t [0 Happywt 0 Popewt] In any possible world ( w) at any time ( t): q q Take the property of being happy (0 Happy) Happy Take the papal office (0 Pope) Pope Extensoinalize both of them (0 Happywt, 0 Popewt) Check whether the holder of the Papal office is happy at that w, t of evaluation ([0 Happywt 0 Popewt])

Method of analysis 1. 2. Assing types to objects that are mentioned by the expression E, i. e. to the objects denoted by subexpressions of E Compose constructions of objects ad 1) to construct the object denoted by E Semantically simple expressions (including idioms) are furnished with Trivialization of the denoted object as their meaning 3. Type checking usually by drawing a derivation tree

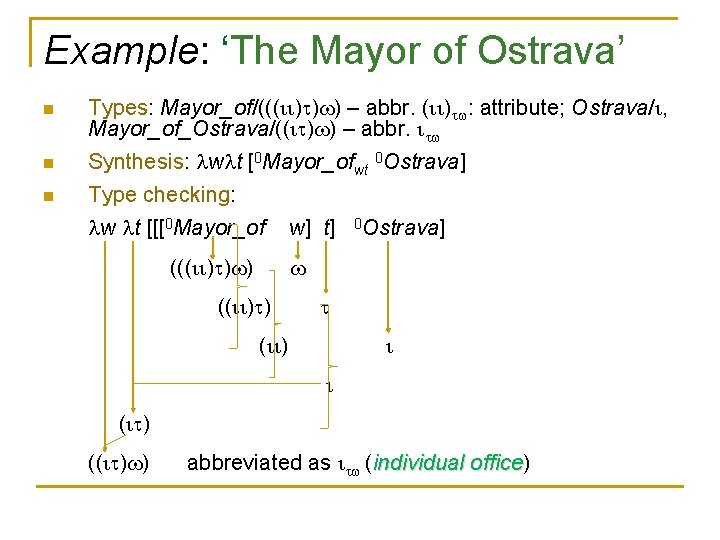
Example: ‘The Mayor of Ostrava’ n Types: Mayor_of/((( ) ) ) – abbr. ( ) : attribute; Ostrava/ , Mayor_of_Ostrava/(( ) ) – abbr. n Synthesis: w t [0 Mayor_ofwt 0 Ostrava] n Type checking: w t [[[0 Mayor_of w] t] 0 Ostrava] ((( ) ) ) (( ) ) ( ) (( ) ) abbreviated as (individual office) office

“The Mayor of Ostrava is rich” n n n Additional type: Rich/( ) Synthesis: w t [0 Richwt w t [0 Mayor_ofwt 0 Ostrava]]wt] Typechecking (shortened): w t [[[0 Richwt w t [0 Mayor_ofwt 0 Ostrava]]wt] ( ) (( ) ) abbr. (proposition) tion

TIL: logical core n constructions + type hierarchy (simple and ramified) n The ramified type hierarchy organizes all higherorder objects: constructions (types n), as well as functions with domain or range in constructions. The simple type hierarchy organizes first-order objects: non-constructions like extensions (individuals, numbers, sets, etc. ), possible-world intensions (functions from possible worlds) and their arguments and values. n

Hyperintensionality n was born out of negative needs, to block invalid inferences q q n n Carnap (1947, §§ 13 ff); there are contexts that are neither extensional nor intensional (attitudes) Cresswell; any context in which substitution of necessary equivalent terms fails is hyperintensional Yet, which inferences are valid in hyperintensional contexts? How hyper are hyperintensions? Which contexts are intensional / hyperintensional? TIL definition is positive: a context is hyperintensional if the very meaning procedure is an object of predication 31

Three kinds of context n n n hyperintensional context: context a meaning construction occurs displayed q so that the very construction is an object of predication q though a construction at least one order higher need to be executed in order to produce the displayed construction intensional context: context a meaning construction occurs executed in order to produce a function f q so that the whole function f is an object of predication q moreover, the executed construction does not occur within another displayed construction extensional context: context the meaning construction is executed in order to produce a particular value of the so-constructed function f at its argument q so that the value of the function f is an object of predication q moreover, the executed construction does not occur within another intensional or hyperintensional context.

Hyperintensionality n n n Extensional logic of hyperintensions Transparency: no context is opaque The same (extensional) logical rules are valid in all kinds of context; q n n Leibniz’s substitution of identicals, existential quantification even into hyperintensional contexts, … Only the types of objects these rules are applied at differ according to a context Anti-contextualism: constructions are assigned to expressions as their context-invariant meanings