National Income Determination ThreeSector National Income Model 1

National Income Determination Three-Sector National Income Model 1

§ Equilibrium in the 3 sector model § Output Expenditure Approach § Withdrawals Injections Approach § The Multiplier § Fiscal Policy 2

§ Aggregate expenditure has three components § E= C + I + G § At the equilibrium, § E=Y § Derive the aggregate expenditure function assuming the following § Yd = Y – T + Q § G= G* § Q= Q* § T= t. Y § I= I* § C= c. Yd 3

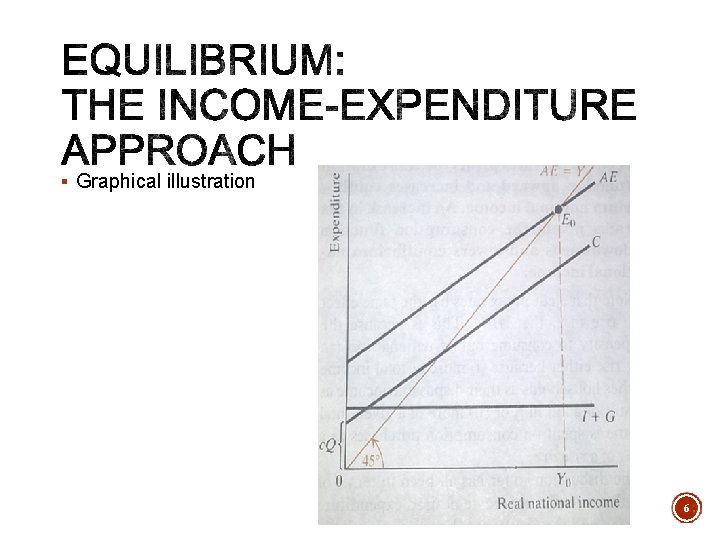
§ Algebraic approach § At equilibrium, Y= E Y = c(1 -t) Y+ c. Q* + I* + G* Y- c(1 – t) Y= c. Q* + I* + G* Y[1 – c(1 – t)] = c. Q* + I* + G* Y = 1/ [1 – c(1 – t)] (c. Q* + I* + G*) § Expenditure depends on two main terms § The sum of the three autonomous flows: Q*, I*, G* § Behavioural patterns of consumption, c, and taxation, t 5

§ Graphical illustration 6

§ What is the effect of changes in autonomous expenditure flows (G, I and c. Q) and the tax rate, t, on national income? 7

§ Graphical illustration § An increase in G, I or c. Q shifts the AE curve upwards § Increase in national income 8

§ An increase in transfer payments (Q) will also increase national income § How? § However, an extra Ghc 1 spent on final government expenditure, G, increases national income by more than Ghc 1 spent on transfer payment, Q. § Why? Discuss… 9

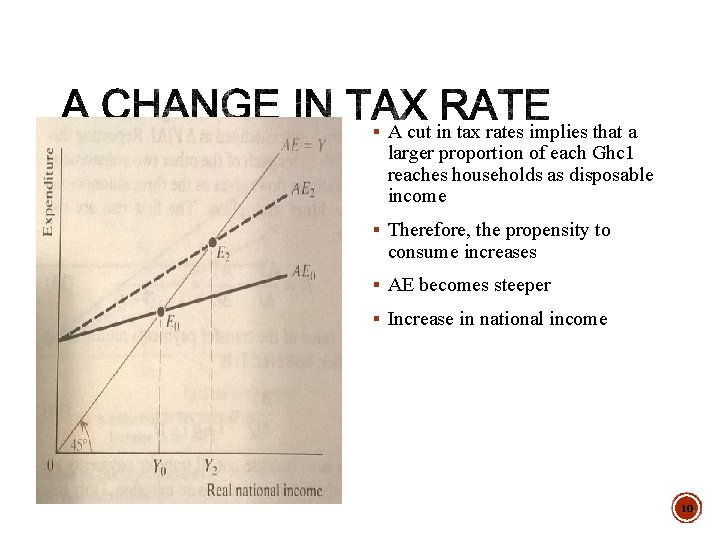
§ A cut in tax rates implies that a larger proportion of each Ghc 1 reaches households as disposable income § Therefore, the propensity to consume increases § AE becomes steeper § Increase in national income 10

§ How large is the change in national income from a given change in autonomous expenditure? § To determine this, we need to solve the following algebraically: § Ye/ I § Ye/ G § Ye/ Q 11

§ Recall from the income expenditure approach § Equilibrium national income is given by Y = 1/ [1 – c(1 – t)] (c. Q* + I* + G*) § Solution? § Ye/ I § Ye/ G § Ye/ Q § What do you notice about the change in income from a change in investment, I*, or government expenditure, G*? § What do you notice about the value of the transfer payments multiplier, Q*? § Is it larger or smaller? Why? § Under what conditions are al three multipliers equal? 12

§ In a 3 -sector model, national income is either consumed, saved or taxed by the government §Y=C+S+T § Given E = C + I + G § In equilibrium, Y = E §C+S+T=C+I+G § S + T = I + G , but G= G + Q (Q= c. Q) § S + T = I + G + c. Q i. e. withdrawals = injections 13

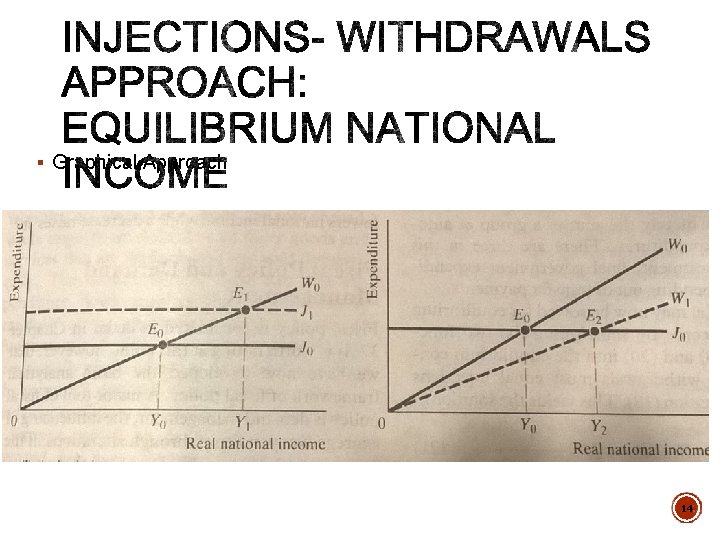
§ Graphical Approach 14

§ Graphical Approach § An increase in any component of aggregate expenditure shifts the injections curve upwards § And vice versa § A fall in the tax rate increases the amount of disposable income, and the propensity for increased consumption § This is illustrated by a flatter (i. e. smaller value of t) withdrawals curve, leading to increased equilibrium national income 15

§ An algebraic approach § We define savings, S= s(Y- T) § i. e. the part of disposable income that is saved § Other assumptions § T= t. Y § Q= Q* § I= I* § G= G* § At the equilibrium, Withdrawals = Injections § Withdrawals = s(1 - t)Y + t. Y = Y[s(1 - t) + t] § Injections = I* + G* + c. Q* § At the equilibrium, § Y =1/ [s(1 - t) + t] x (I* + G* + c. Q*) § Is this the same equilibrium as obtained under the income-expenditure approach? § Derive the multipliers for investment and government expenditures, and transfer payments. 16

§ Using the mechanistic Keynes Theory of National Income, explain the causes and solutions to the Great Depression of 1929. 17

§ Dr Monica P. Lambon-Quayefio § Money and its Functions § The origin of money § Modern money and definition of monetary aggregates § Commercial Banks and Money Creation § The Central Bank and its functions 18