NAT traversal problem r client want to connect
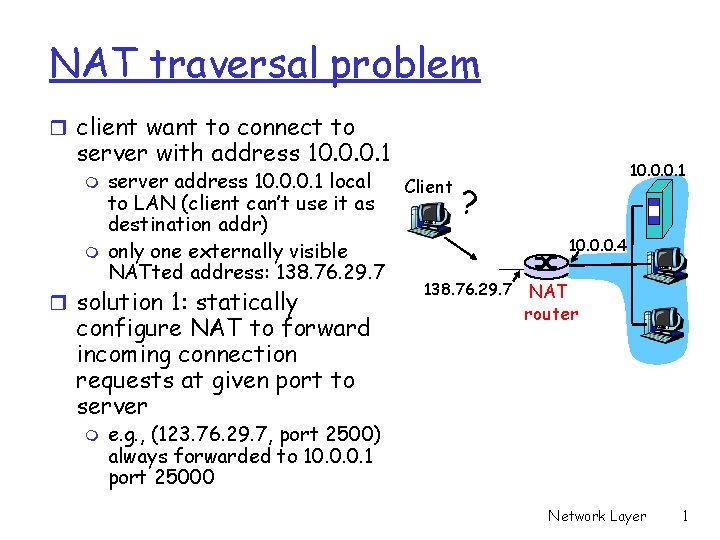
NAT traversal problem r client want to connect to server with address 10. 0. 0. 1 m m server address 10. 0. 0. 1 local Client to LAN (client can’t use it as destination addr) only one externally visible NATted address: 138. 76. 29. 7 r solution 1: statically configure NAT to forward incoming connection requests at given port to server m 10. 0. 0. 1 ? 138. 76. 29. 7 10. 0. 0. 4 NAT router e. g. , (123. 76. 29. 7, port 2500) always forwarded to 10. 0. 0. 1 port 25000 Network Layer 1
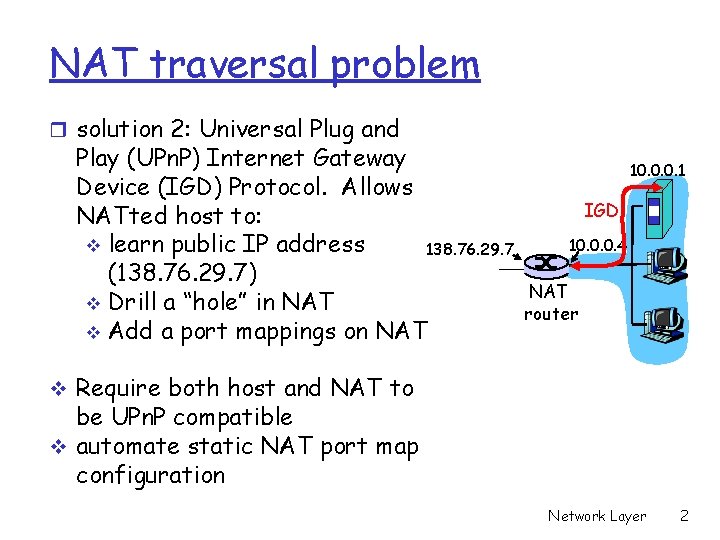
NAT traversal problem r solution 2: Universal Plug and Play (UPn. P) Internet Gateway Device (IGD) Protocol. Allows NATted host to: v learn public IP address 138. 76. 29. 7 (138. 76. 29. 7) v Drill a “hole” in NAT v Add a port mappings on NAT 10. 0. 0. 1 IGD 10. 0. 0. 4 NAT router v Require both host and NAT to be UPn. P compatible v automate static NAT port map configuration Network Layer 2
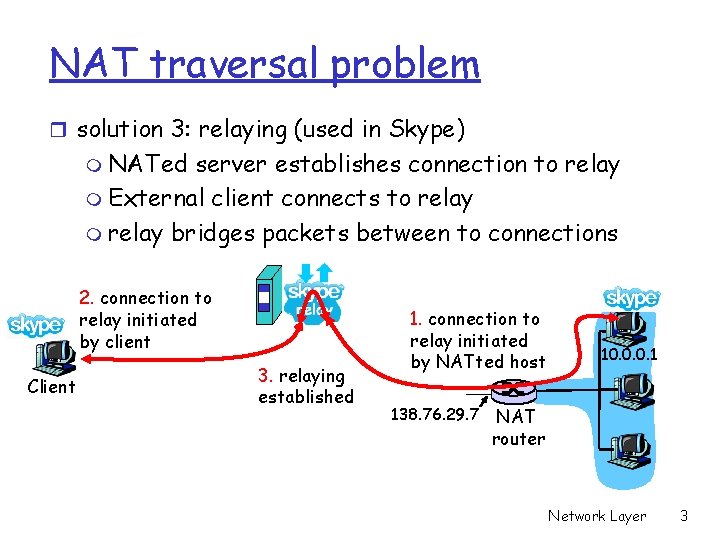
NAT traversal problem r solution 3: relaying (used in Skype) m NATed server establishes connection to relay m External client connects to relay m relay bridges packets between to connections 2. connection to relay initiated by client Client 3. relaying established 1. connection to relay initiated by NATted host 138. 76. 29. 7 10. 0. 0. 1 NAT router Network Layer 3
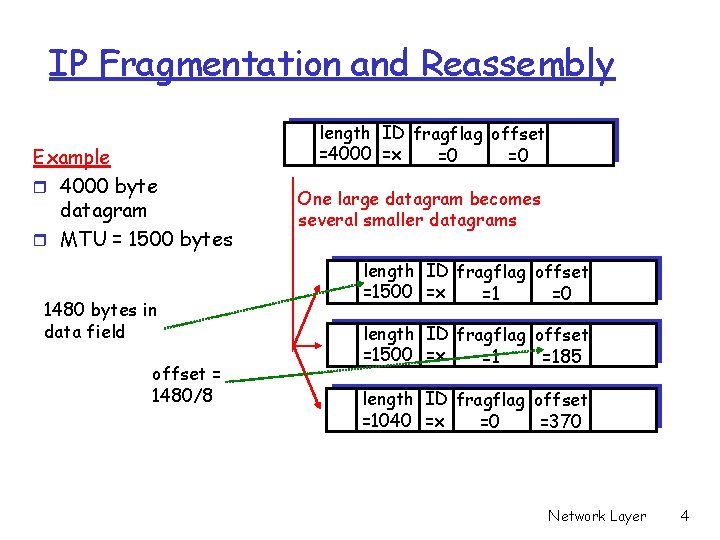
IP Fragmentation and Reassembly Example r 4000 byte datagram r MTU = 1500 bytes 1480 bytes in data field offset = 1480/8 length ID fragflag offset =4000 =x =0 =0 One large datagram becomes several smaller datagrams length ID fragflag offset =1500 =x =1 =0 length ID fragflag offset =1500 =x =1 =185 length ID fragflag offset =1040 =x =0 =370 Network Layer 4

DHCP: Dynamic Host Configuration Protocol Goal: allow host to dynamically obtain its IP address from network server when it joins network Can renew its lease on address in use Allows reuse of addresses (only hold address while connected an “on” Support for mobile users who want to join network (more shortly) DHCP overview: m host broadcasts “DHCP discover” msg m DHCP server responds with “DHCP offer” msg m host requests IP address: “DHCP request” msg m DHCP server sends address: “DHCP ack” msg Network Layer 5
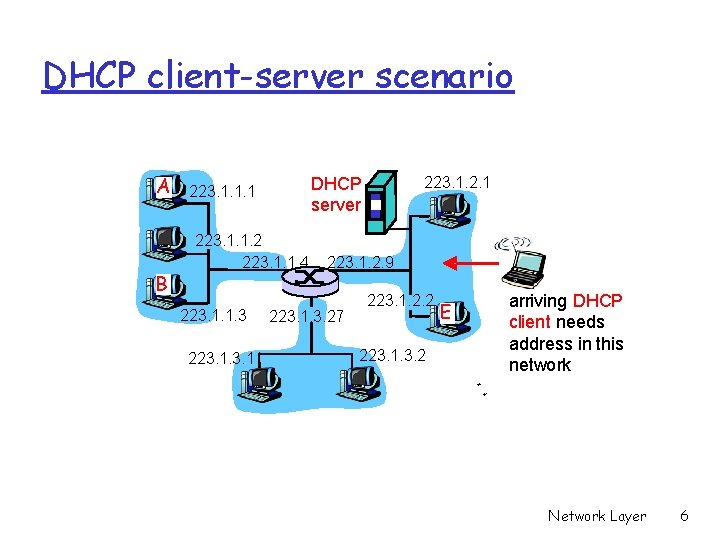
DHCP client-server scenario A B 223. 1. 1. 2 223. 1. 1. 4 223. 1. 1. 3 223. 1. 2. 1 DHCP server 223. 1. 1. 1 223. 1. 2. 9 223. 1. 3. 27 223. 1. 2. 2 223. 1. 3. 2 E arriving DHCP client needs address in this network Network Layer 6
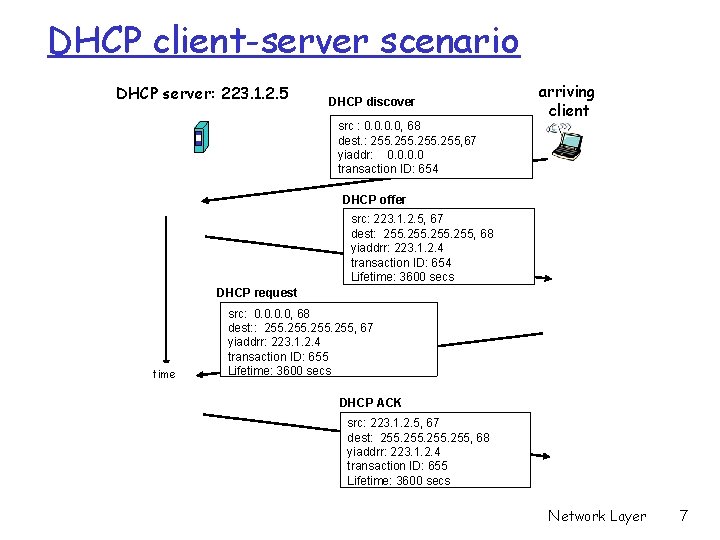
DHCP client-server scenario DHCP server: 223. 1. 2. 5 DHCP discover src : 0. 0, 68 dest. : 255, 67 yiaddr: 0. 0 transaction ID: 654 arriving client DHCP offer src: 223. 1. 2. 5, 67 dest: 255, 68 yiaddrr: 223. 1. 2. 4 transaction ID: 654 Lifetime: 3600 secs DHCP request time src: 0. 0, 68 dest: : 255, 67 yiaddrr: 223. 1. 2. 4 transaction ID: 655 Lifetime: 3600 secs DHCP ACK src: 223. 1. 2. 5, 67 dest: 255, 68 yiaddrr: 223. 1. 2. 4 transaction ID: 655 Lifetime: 3600 secs Network Layer 7

Chapter 4: Network Layer r 4. 1 Introduction r 4. 2 Virtual circuit and datagram networks r 4. 3 What’s inside a router r 4. 4 IP: Internet Protocol m m Datagram format IPv 4 addressing ICMP IPv 6 r 4. 5 Routing algorithms m Link state m Distance Vector m Hierarchical routing r 4. 6 Routing in the Internet m m m RIP OSPF BGP r 4. 7 Broadcast and multicast routing Network Layer 8

ICMP: Internet Control Message Protocol r used by hosts & routers to communicate network-level information m error reporting: unreachable host, network, port, protocol m echo request/reply (used by ping) r network-layer “above” IP: m ICMP msgs carried in IP datagrams m Not built on TCP! r ICMP message: type, code plus first 8 bytes of IP datagram causing error Type 0 3 3 3 4 Code 0 0 1 2 3 6 7 0 8 9 10 11 12 0 0 0 description echo reply (ping) dest. network unreachable dest host unreachable dest protocol unreachable dest port unreachable dest network unknown dest host unknown source quench (congestion control - not used) echo request (ping) route advertisement router discovery TTL expired bad IP header Network Layer 9

Traceroute and ICMP r Source sends series of UDP segments to dest m m m First has TTL =1 Second has TTL=2, etc. Unlikely port number r When nth datagram arrives to nth router: m m m Router discards datagram And sends to source an ICMP message (type 11, code 0) Message includes name of router& IP address Ethereal example r When ICMP message arrives, source calculates RTT r Traceroute does this 3 times Stopping criterion r UDP segment eventually arrives at destination host r Destination returns ICMP “host unreachable” packet (type 3, code 3) r When source gets this ICMP, stops. Network Layer 10

Chapter 4: Network Layer r 4. 1 Introduction r 4. 2 Virtual circuit and datagram networks r 4. 3 What’s inside a router r 4. 4 IP: Internet Protocol m m Datagram format IPv 4 addressing ICMP IPv 6 r 4. 5 Routing algorithms m Link state m Distance Vector m Hierarchical routing r 4. 6 Routing in the Internet m m m RIP OSPF BGP r 4. 7 Broadcast and multicast routing Network Layer 11

IPv 6 r Initial motivation: 32 -bit address space soon to be completely allocated. r Additional motivation: m header format helps speed processing/forwarding m header changes to facilitate Qo. S m Checksum: removed entirely to reduce processing time at each hop IPv 6 datagram format: m fixed-length 40 byte header m no fragmentation allowed Very slow take off • IPv 4 still has space (CIDR, DHCP, NAT) • Too trouble to upgrade Network Layer 12
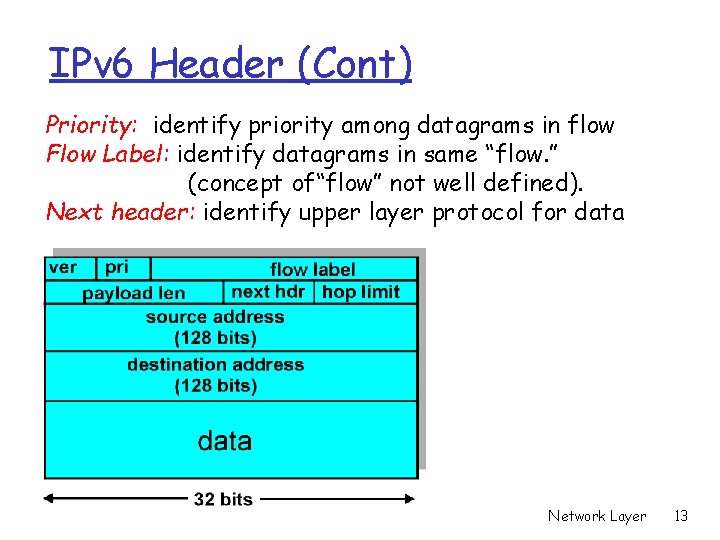
IPv 6 Header (Cont) Priority: identify priority among datagrams in flow Flow Label: identify datagrams in same “flow. ” (concept of“flow” not well defined). Next header: identify upper layer protocol for data Network Layer 13

Transition From IPv 4 To IPv 6 r Not all routers can be upgraded simultaneous m no “flag days” m How will the network operate with mixed IPv 4 and IPv 6 routers? r Tunneling: IPv 6 carried as payload in IPv 4 datagram among IPv 4 routers Network Layer 14
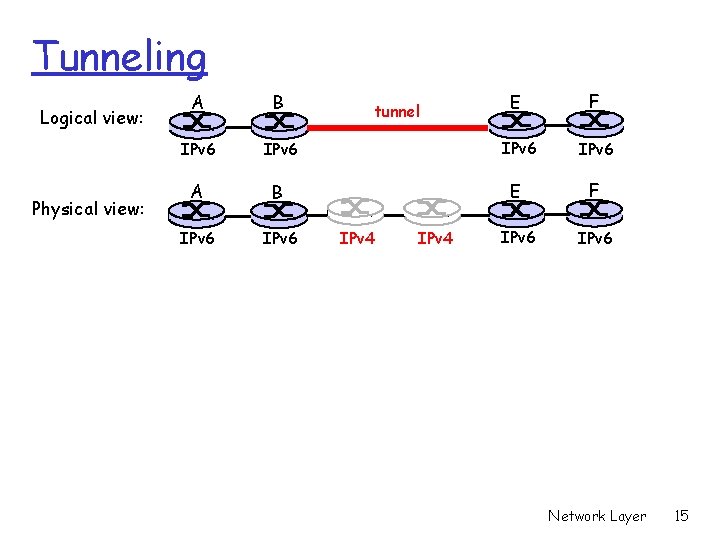
Tunneling Logical view: Physical view: E F IPv 6 IPv 6 A B IPv 6 tunnel IPv 4 Network Layer 15
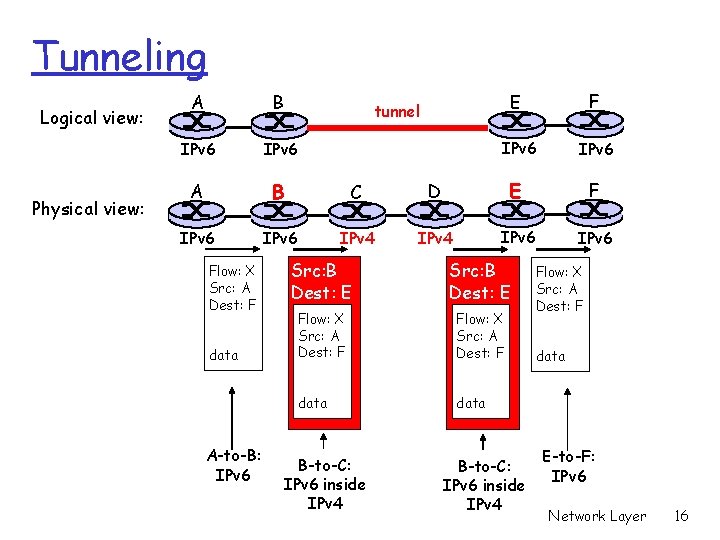
Tunneling Logical view: Physical view: A B IPv 6 A B C IPv 6 IPv 4 Flow: X Src: A Dest: F data A-to-B: IPv 6 E F IPv 6 D E F IPv 4 IPv 6 tunnel Src: B Dest: E Flow: X Src: A Dest: F data B-to-C: IPv 6 inside IPv 4 Flow: X Src: A Dest: F data E-to-F: IPv 6 Network Layer 16

Chapter 4: Network Layer r 4. 1 Introduction r 4. 2 Virtual circuit and datagram networks r 4. 3 What’s inside a router r 4. 4 IP: Internet Protocol m m Datagram format IPv 4 addressing ICMP IPv 6 r 4. 5 Routing algorithms m Link state m Distance Vector m Hierarchical routing r 4. 6 Routing in the Internet m m m RIP OSPF BGP r 4. 7 Broadcast and multicast routing Network Layer 17

Routing Algorithm classification Global or decentralized information? Global: r all routers have complete topology, link cost info r “link state” algorithms Decentralized: r router knows physicallyconnected neighbors, link costs to neighbors r iterative process of computation, exchange of info with neighbors r “distance vector” algorithms Static or dynamic? Static: r routes change slowly over time Dynamic: r routes change more quickly m periodic update m in response to link cost changes Network Layer 18

Chapter 4: Network Layer r 4. 1 Introduction r 4. 2 Virtual circuit and datagram networks r 4. 3 What’s inside a router r 4. 4 IP: Internet Protocol m m Datagram format IPv 4 addressing ICMP IPv 6 r 4. 5 Routing algorithms m Link state m Distance Vector m Hierarchical routing r 4. 6 Routing in the Internet m m m RIP OSPF BGP r 4. 7 Broadcast and multicast routing Network Layer 19
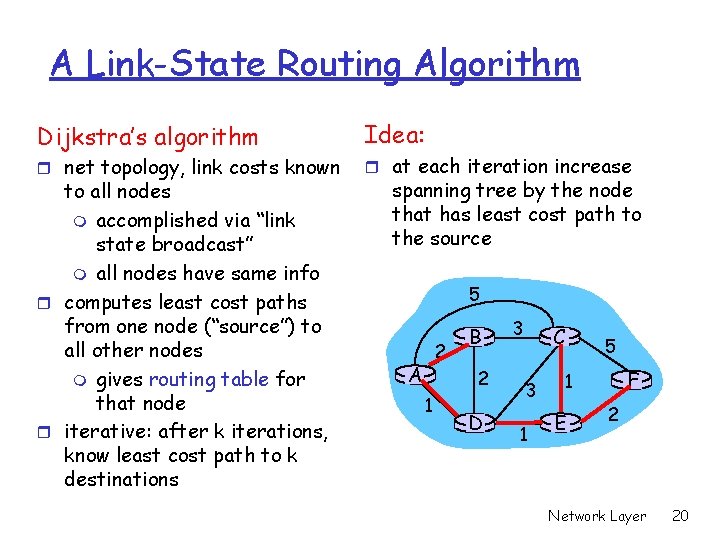
A Link-State Routing Algorithm Dijkstra’s algorithm r net topology, link costs known to all nodes m accomplished via “link state broadcast” m all nodes have same info r computes least cost paths from one node (“source”) to all other nodes m gives routing table for that node r iterative: after k iterations, know least cost path to k destinations Idea: r at each iteration increase spanning tree by the node that has least cost path to the source 5 2 A B 2 1 D 3 C 3 1 5 F 1 E 2 Network Layer 20
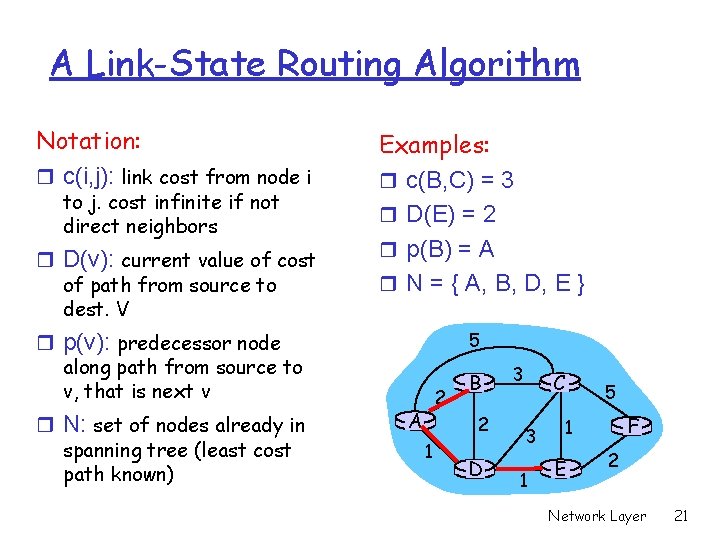
A Link-State Routing Algorithm Notation: r c(i, j): link cost from node i to j. cost infinite if not direct neighbors r D(v): current value of cost of path from source to dest. V Examples: r c(B, C) = 3 r D(E) = 2 r p(B) = A r N = { A, B, D, E } 5 r p(v): predecessor node along path from source to v, that is next v r N: set of nodes already in spanning tree (least cost path known) 2 A B 2 1 D 3 C 3 1 5 F 1 E 2 Network Layer 21

Dijsktra’s Algorithm 1 Initialization: 2 N = {A} 3 for all nodes v 4 if v adjacent to A 5 then D(v) = c(A, v) 6 else D(v) = infinity 7 8 Loop 9 find w not in N such that D(w) is a minimum 10 add w to N 11 update D(v) for all v adjacent to w and not in N: 12 D(v) = min( D(v), D(w) + c(w, v) ) 13 /* new cost to v is either old cost to v or known 14 shortest path cost to w plus cost from w to v */ 15 until all nodes in N Network Layer 22
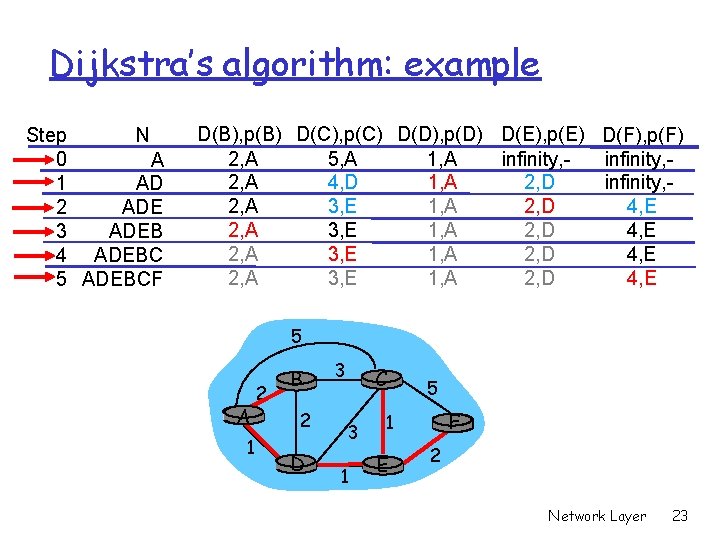
Dijkstra’s algorithm: example Step N 0 A 1 AD 2 ADE 3 ADEB 4 ADEBC 5 ADEBCF D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 5, A 1, A infinity, 2, A 4, D 1, A 2, D infinity, 2, A 3, E 1, A 2, D 4, E 5 A 1 2 B 2 D 3 C 3 1 5 F 1 E 2 Network Layer 23
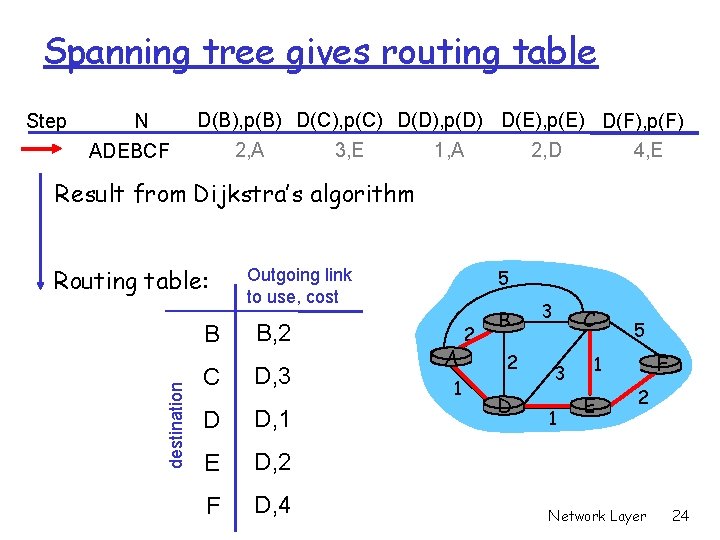
Spanning tree gives routing table Step N ADEBCF D(B), p(B) D(C), p(C) D(D), p(D) D(E), p(E) D(F), p(F) 2, A 3, E 1, A 2, D 4, E Result from Dijkstra’s algorithm destination Routing table: 5 Outgoing link to use, cost B B, 2 C D, 3 D D, 1 E D, 2 F D, 4 A 1 2 B 2 D 3 C 3 1 5 F 1 E 2 Network Layer 24
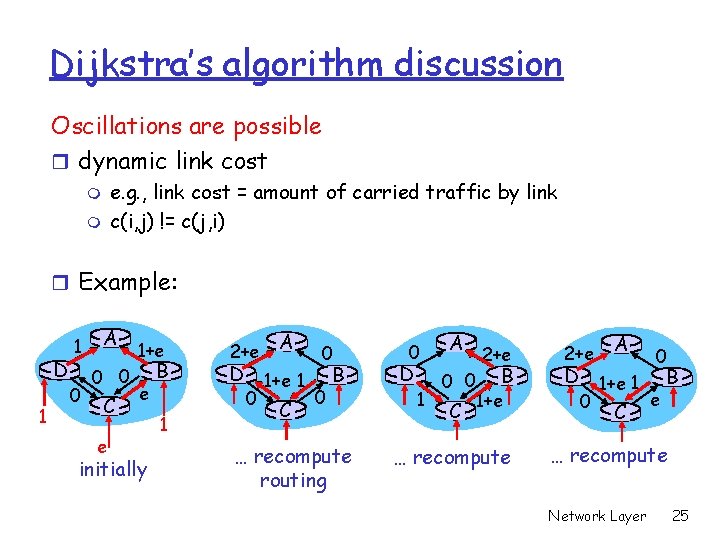
Dijkstra’s algorithm discussion Oscillations are possible r dynamic link cost e. g. , link cost = amount of carried traffic by link c(i, j) != c(j, i) m m r Example: D 1 1 0 A 0 0 C e 1+e e initially B 1 2+e A 0 D 1+e 1 B 0 0 C … recompute routing 0 D 1 A 0 0 C 2+e B 1+e … recompute 2+e A 0 D 1+e 1 B e 0 C … recompute Network Layer 25

Chapter 4: Network Layer r 4. 1 Introduction r 4. 2 Virtual circuit and datagram networks r 4. 3 What’s inside a router r 4. 4 IP: Internet Protocol m m Datagram format IPv 4 addressing ICMP IPv 6 r 4. 5 Routing algorithms m Link state m Distance Vector m Hierarchical routing r 4. 6 Routing in the Internet m m m RIP OSPF BGP r 4. 7 Broadcast and multicast routing Network Layer 26

Distance Vector Algorithm (1) Bellman-Ford Equation (dynamic programming) Define dx(y) : = cost of least-cost path from x to y Then dx(y) = minv {c(x, v) + dv(y) } where min is taken over all neighbors of x Network Layer 27
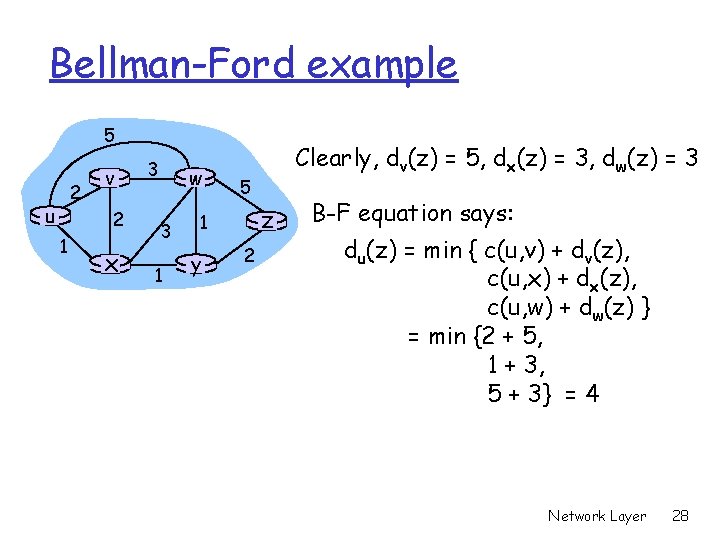
Bellman-Ford example 5 2 u v 2 1 x 3 w 3 1 5 z 1 y Clearly, dv(z) = 5, dx(z) = 3, dw(z) = 3 2 B-F equation says: du(z) = min { c(u, v) + dv(z), c(u, x) + dx(z), c(u, w) + dw(z) } = min {2 + 5, 1 + 3, 5 + 3} = 4 Network Layer 28

Distance Vector Algorithm (3) r Dx(y) = estimate of least cost from x to y r Distance vector: Dx = [Dx(y): y є N ] r Node x knows cost to each neighbor v: c(x, v) r Node x maintains Dx = [Dx(y): y є N ] r Node x also maintains its neighbors’ distance vectors m For each neighbor v, x maintains Dv = [Dv(y): y є N ] Network Layer 29

Distance vector algorithm (4) Basic idea: r Each node periodically sends its own distance vector estimate to neighbors r When a node x receives new DV estimate from neighbor, it updates its own DV using B-F equation: Dx(y) ← minv{c(x, v) + Dv(y)} for each node y ∊ N r Under minor, natural conditions, the estimate Dx(y) converge the actual least cost dx(y) Network Layer 30
Distance Vector Algorithm (5) Iterative, asynchronous: each local iteration caused by: r local link cost change r DV update message from neighbor Distributed: r each node notifies neighbors only when its DV changes m neighbors then notify their neighbors if necessary Each node: wait for (change in local link, cost of msg from neighbor) recompute estimates if DV to any dest has changed, notify neighbors Network Layer 31
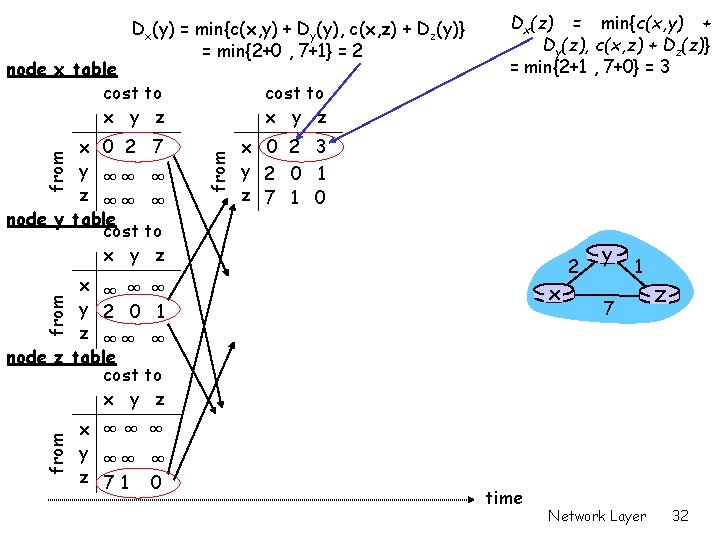
Dx(y) = min{c(x, y) + Dy(y), c(x, z) + Dz(y)} = min{2+0 , 7+1} = 2 node x table cost to x y z from x 0 2 7 y ∞∞ ∞ z ∞∞ ∞ node y table cost to x y z Dx(z) = min{c(x, y) + Dy(z), c(x, z) + Dz(z)} = min{2+1 , 7+0} = 3 x 0 2 3 y 2 0 1 z 7 1 0 x ∞ ∞ ∞ y 2 0 1 z ∞∞ ∞ node z table cost to x y z from x x ∞∞ ∞ y ∞∞ ∞ z 71 0 time 2 y 1 7 Network Layer z 32
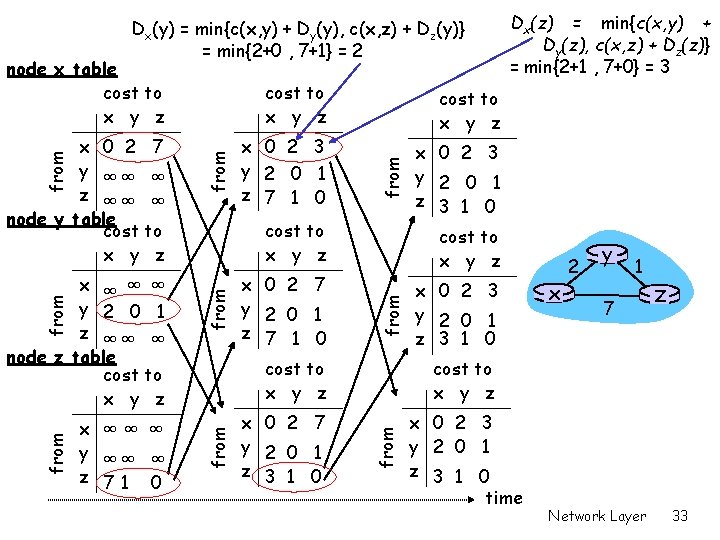
Dx(y) = min{c(x, y) + Dy(y), c(x, z) + Dz(y)} = min{2+0 , 7+1} = 2 node x table cost to x y z x ∞∞ ∞ y ∞∞ ∞ z 71 0 from x 0 2 7 y 2 0 1 z 7 1 0 cost to x y z x 0 2 7 y 2 0 1 z 3 1 0 x 0 2 3 y 2 0 1 z 3 1 0 cost to x y z x 0 2 3 y 2 0 1 z 3 1 0 x 2 y 1 7 z cost to x y z from x ∞ ∞ ∞ y 2 0 1 z ∞∞ ∞ node z table cost to x y z x 0 2 3 y 2 0 1 z 7 1 0 cost to x y z from x 0 2 7 y ∞∞ ∞ z ∞∞ ∞ node y table cost to x y z Dx(z) = min{c(x, y) + Dy(z), c(x, z) + Dz(z)} = min{2+1 , 7+0} = 3 x 0 2 3 y 2 0 1 z 3 1 0 time Network Layer 33

Distance Vector: link cost changes Link cost changes: r node detects local link cost change r updates routing info, recalculates distance vector r if DV changes, notify neighbors “good news travels fast” 1 x 4 y 50 1 z At time t 0, y detects the link-cost change, updates its DV, and informs its neighbors. At time t 1, z receives the update from y and updates its table. It computes a new least cost to x and sends its neighbors its DV. At time t 2, y receives z’s update and updates its distance table. y’s least costs do not change and hence y does not send any message to z. Network Layer 34

Distance Vector: link cost changes Link cost changes: r good news travels fast r bad news travels slow - “count to infinity” problem! r 44 iterations before algorithm stabilizes: see text 60 x 4 y 50 1 z Poisoned reverse: r If Z routes through Y to get to X : m Z tells Y its (Z’s) distance to X is infinite (so Y won’t route to X via Z) r will this completely solve count to infinity problem? Network Layer 35

Comparison of LS and DV algorithms Message complexity r LS: with n nodes, E links, O(n. E) msgs sent r DV: exchange between neighbors only m convergence time varies Speed of Convergence r LS: O(n 2) algorithm requires O(n. E) msgs m may have oscillations r DV: convergence time varies m may be routing loops m count-to-infinity problem Robustness: what happens if router malfunctions? LS: m m node can advertise incorrect link cost each node computes only its own table DV: m m DV node can advertise incorrect path cost each node’s table used by others • error propagate thru network Network Layer 36
- Slides: 36