Naming Triangles are named by using its vertices
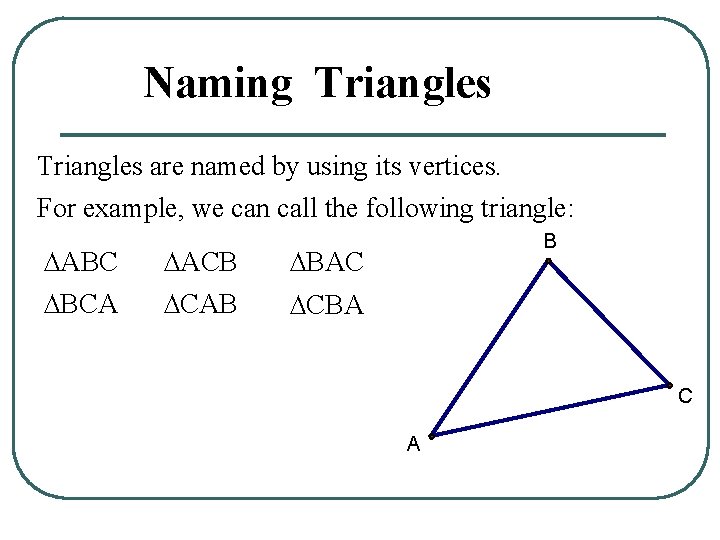
Naming Triangles are named by using its vertices. For example, we can call the following triangle: ∆ABC ∆ACB ∆BAC ∆BCA ∆CAB ∆CBA B C A
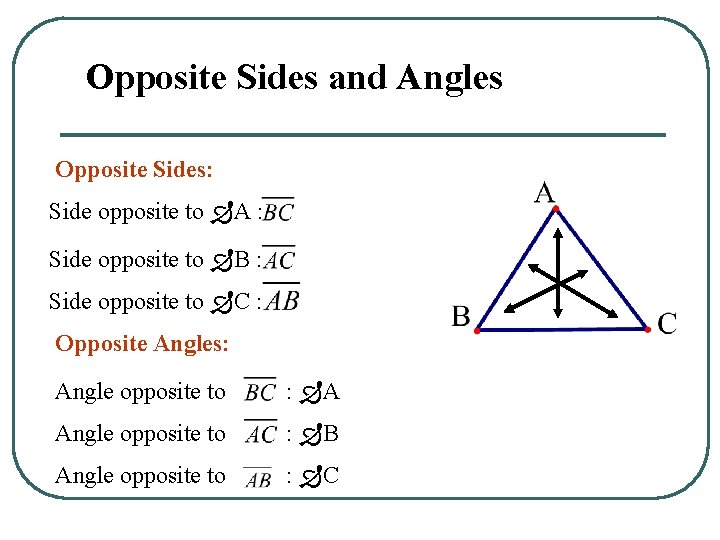
Opposite Sides and Angles Opposite Sides: Side opposite to A : Side opposite to B : Side opposite to C : Opposite Angles: Angle opposite to : A Angle opposite to : B Angle opposite to : C
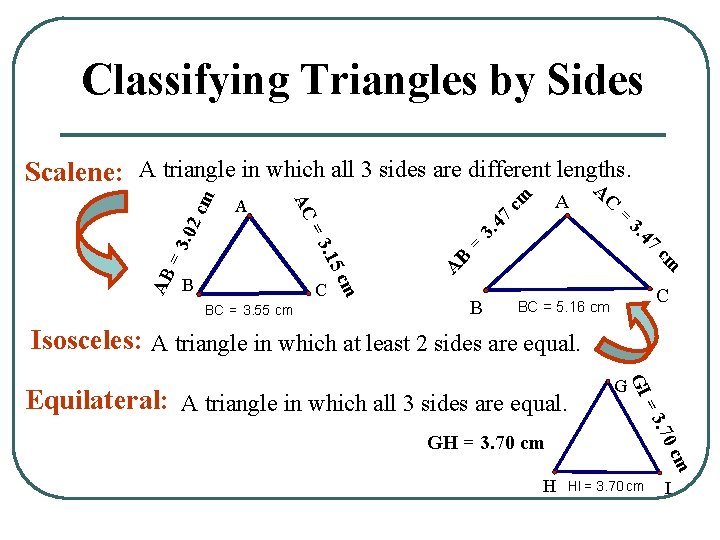
Classifying Triangles by Sides cm 47 3. = B A cm =3. 02 47 3. AB = BC = 3. 55 cm C C m 5 c 3. 1 B A A A = AC cm Scalene: A triangle in which all 3 sides are different lengths. B C BC = 5. 16 cm Isosceles: A triangle in which at least 2 sides are equal. cm H . 70 =3 GH = 3. 70 cm GI Equilateral: A triangle in which all 3 sides are equal. G HI = 3. 70 cm I
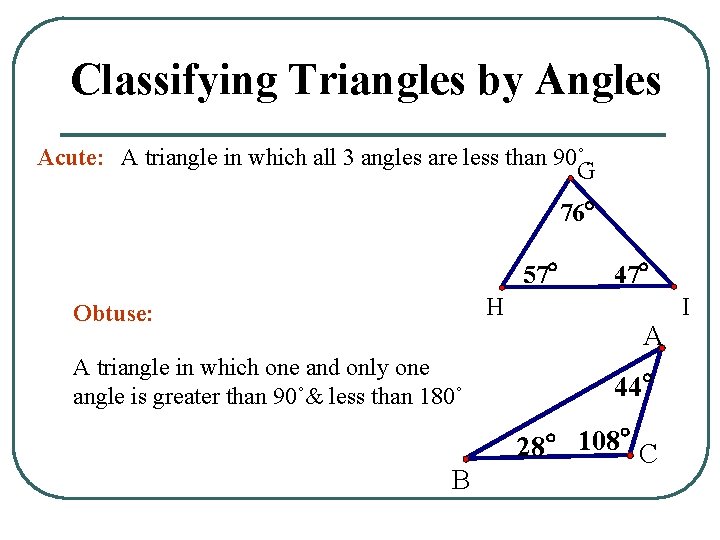
Classifying Triangles by Angles Acute: A triangle in which all 3 angles are less than 90˚. G 76° 57° H Obtuse: A triangle in which one and only one angle is greater than 90˚& less than 180˚ B 47° A 44° 28° 108° C I
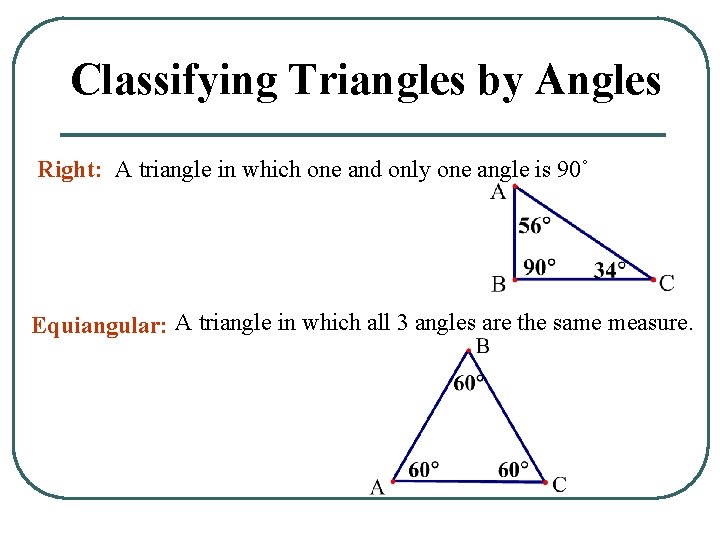
Classifying Triangles by Angles Right: A triangle in which one and only one angle is 90˚ Equiangular: A triangle in which all 3 angles are the same measure.
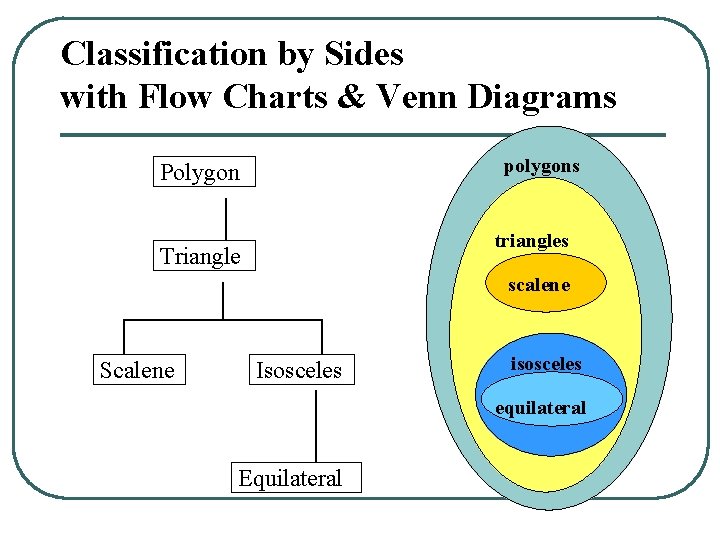
Classification by Sides with Flow Charts & Venn Diagrams polygons Polygon triangles Triangle scalene Scalene Isosceles isosceles equilateral Equilateral
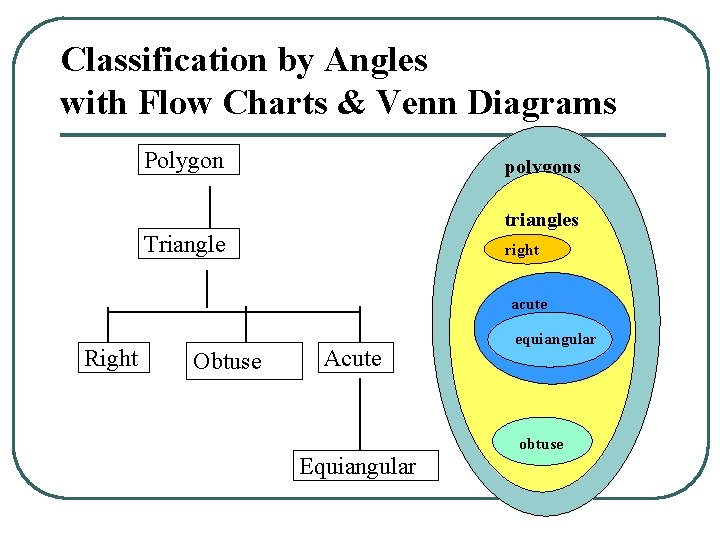
Classification by Angles with Flow Charts & Venn Diagrams Polygon polygons triangles Triangle right acute Right Obtuse Acute equiangular obtuse Equiangular

Theorems & Corollaries Triangle Sum Theorem: The sum of the interior angles in a triangle is 180˚. Third Angle Theorem: If two angles of one triangle are congruent to two angles of a second triangle, then the third angles of the triangles are congruent. Corollary 1: Each angle in an equiangular triangle is 60˚. Corollary 2: Acute angles in a right triangle are complementary. Corollary 3: There can be at most one right or obtuse angle in a triangle.
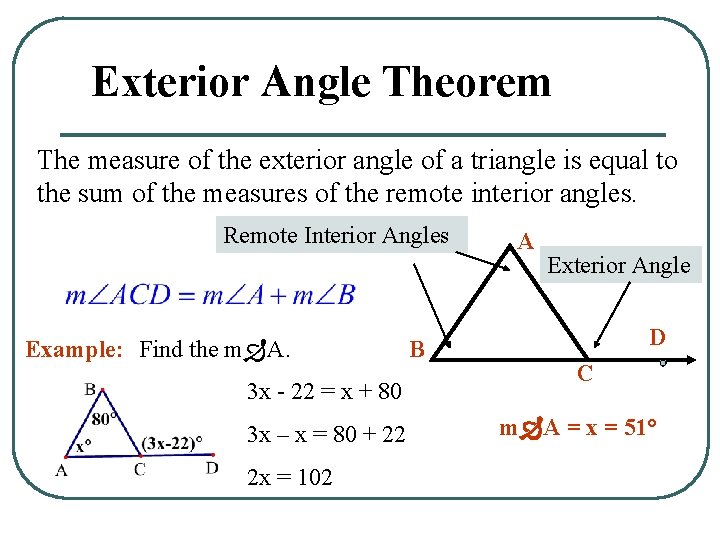
Exterior Angle Theorem The measure of the exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. Remote Interior Angles Example: Find the m A. 3 x - 22 = x + 80 3 x – x = 80 + 22 2 x = 102 B A Exterior Angle D C m A = x = 51°

Median - Special Segment of Triangle Definition: A segment from the vertex of the triangle to the midpoint of the opposite side. Since there are three vertices, there are three medians. C A B F E D In the figure C, E and F are the midpoints of the sides of the triangle.
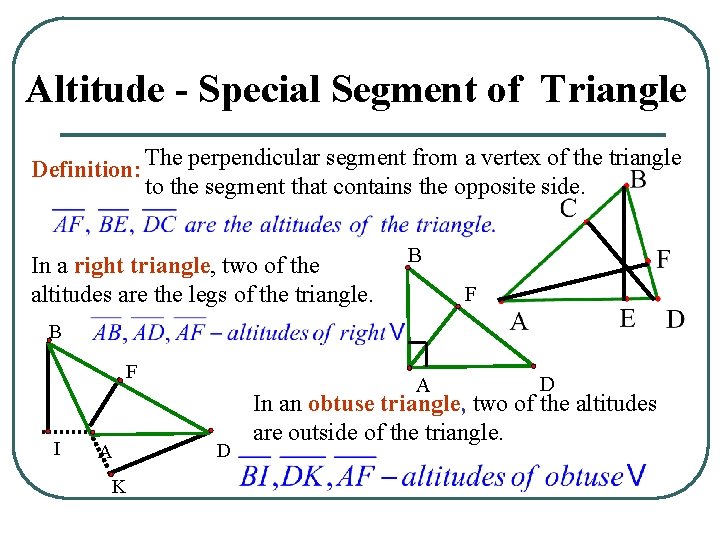
Altitude - Special Segment of Triangle Definition: The perpendicular segment from a vertex of the triangle to the segment that contains the opposite side. In a right triangle, two of the altitudes are the legs of the triangle. B F I A K A D D In an obtuse triangle, two of the altitudes are outside of the triangle.
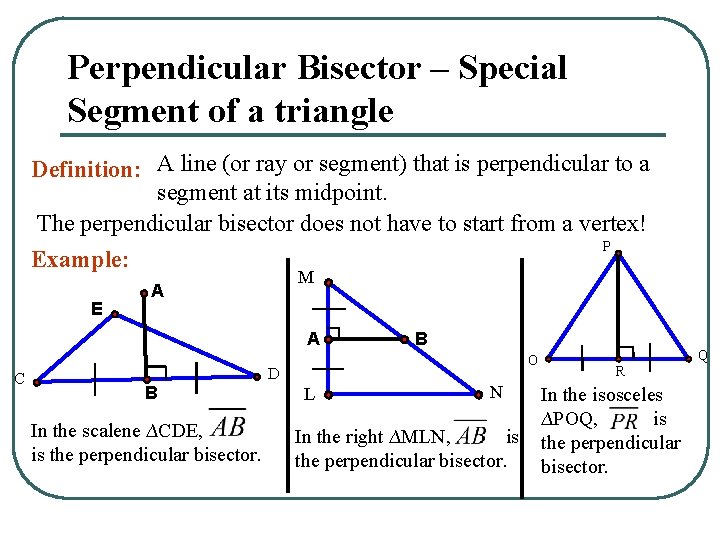
Perpendicular Bisector – Special Segment of a triangle Definition: A line (or ray or segment) that is perpendicular to a segment at its midpoint. The perpendicular bisector does not have to start from a vertex! P Example: E M A A C O D B In the scalene ∆CDE, is the perpendicular bisector. B L N In the right ∆MLN, is the perpendicular bisector. Q R In the isosceles ∆POQ, is the perpendicular bisector.
- Slides: 12