Name Paper 3 Higher Predicted Calculator Date Time




















- Slides: 39

Name: Paper 3 Higher Predicted Calculator Date: Time: 1 hour 30 minutes Total marks available: 80 Total marks achieved:

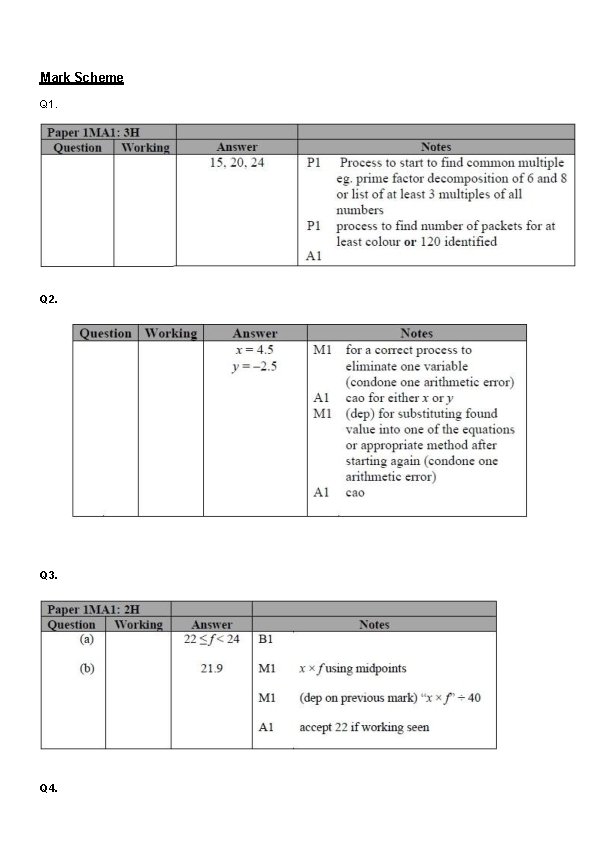
Q 1. Liz buys packets of coloured buttons. There are 8 red buttons in each packet of red buttons. There are 6 silver buttons in each packet of silver buttons. There are 5 gold buttons in each packet of gold buttons. Liz buys equal numbers of red buttons, silver buttons and gold buttons. How many packets of each colour of buttons did Liz buy? . . . . packets of red buttons. . . . packets of silver buttons. . . . packets of gold buttons (Total for question = 3 marks) Q 2. Solve the simultaneous equations 2 x – 4 y = 19 3 x + 5 y = 1 x =. . . . y =. . . . (Total for question = 4 marks)

Q 1. Liz buys packets of coloured buttons. There are 8 red buttons in each packet of red buttons. There are 6 silver buttons in each packet of silver buttons. There are 5 gold buttons in each packet of gold buttons. Liz buys equal numbers of red buttons, silver buttons and gold buttons. How many packets of each colour of buttons did Liz buy? 8 16 24 32 40 48 56 64 72 80 88 96 104 112 120 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90 96 102 108 114 120 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 ÷ 8 = 15 120 ÷ 6 = 20 120 ÷ 5 = 24 15. . . . packets of red buttons 20 . . . . packets of silver buttons 24 . . . . packets of gold buttons (Total for question = 3 marks) Q 2. Solve the simultaneous equations 2 x – 4 y = 19 3 x + 5 y = 1 6 x-12 y = 57 6 x+10 y= 2 -22 y=55 y= -2. 5 3 x + - 12. 5=1 3 x = 13. 5 x = 4. 5 x =. . . . -2. 5 y =. . . . (Total for question = 4 marks)

Q 3. The table shows some information about the foot lengths of 40 adults. (a) Write down the modal class interval. . . . (1) (b) Calculate an estimate for the mean foot length. . . . cm (3) (Total for question = 4 marks) Q 4. The diagram shows a regular octagon and a regular hexagon.

Q 3. The table shows some information about the foot lengths of 40 adults. (a) Write down the modal class interval. 22≤f<24. . . . (1) (b) Calculate an estimate for the mean foot length. (17 x 3)+(19 x 6)+(21 x 10)+(23 x 12)+(25 x 9) = 876÷ 40 = 21. 9 . . . . cm (3) (Total for question = 4 marks) Q 4. The diagram shows a regular octagon and a regular hexagon.

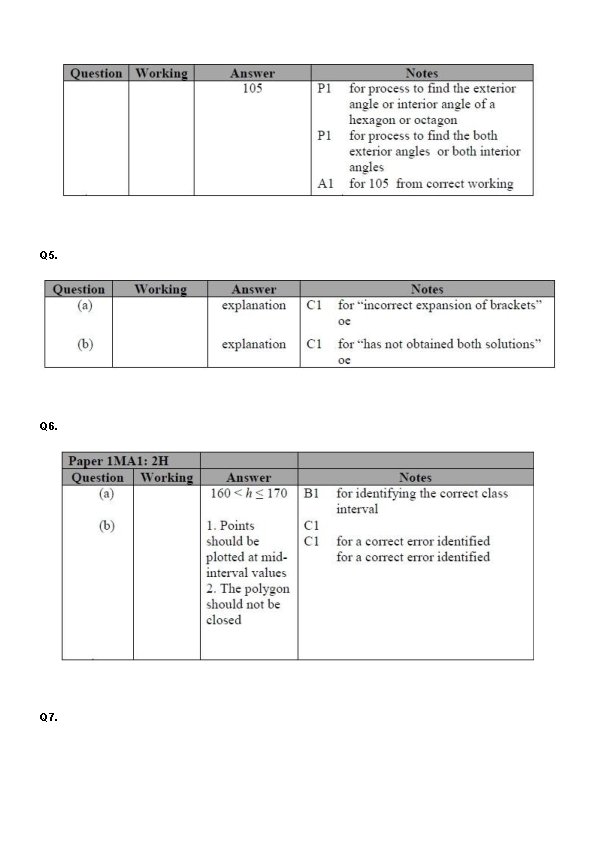
Find the size of the angle marked x You must show all your working. x =. . . . º (Total for question = 3 marks) Q 5. Steve is asked to solve the equation 5(x + 2) = 47. Here is his working. 5(x + 2) = 47 5 x + 2 = 47 5 x = 45 x=9 Steve's answer is wrong. (a) What mistake did he make? . . . . . . . . . . . . . . . . . (1) Liz is asked to solve the equation 3 x 2 + 8 = 83 Here is her working. 3 x 2 + 8 = 83 3 x 2 = 75 x 2 = 25 x=5 (b) Explain what is wrong with Liz's answer. . . . . . . . . . . . . . . . . . (1) (Total for question = 2 marks)

Find the size of the angle marked x You must show all your working. (8 -2) x 180 = 1080 ÷ 8= 135 (6 -2) x 180 = 720 ÷ 6 = 120 360 -135 – 120 = 105 x =. . . . º (Total for question = 3 marks) Q 5. Steve is asked to solve the equation 5(x + 2) = 47. Here is his working. 5(x + 2) = 47 5 x + 2 = 47 5 x = 45 x=9 Steve's answer is wrong. (a) What mistake did he make? . . . . . . . . . Expanded the brackets incorrectly should be 5 x + 10 . . . . . . . . . (1) Liz is asked to solve the equation 3 x 2 + 8 = 83 Here is her working. 3 x 2 + 8 = 83 3 x 2 = 75 x 2 = 25 x=5 (b) Explain what is wrong with Liz's answer. . . . . . . . . A square root has both positive and negative roots eg +5 and -5 . . . . . . . . . (1) (Total for question = 2 marks)

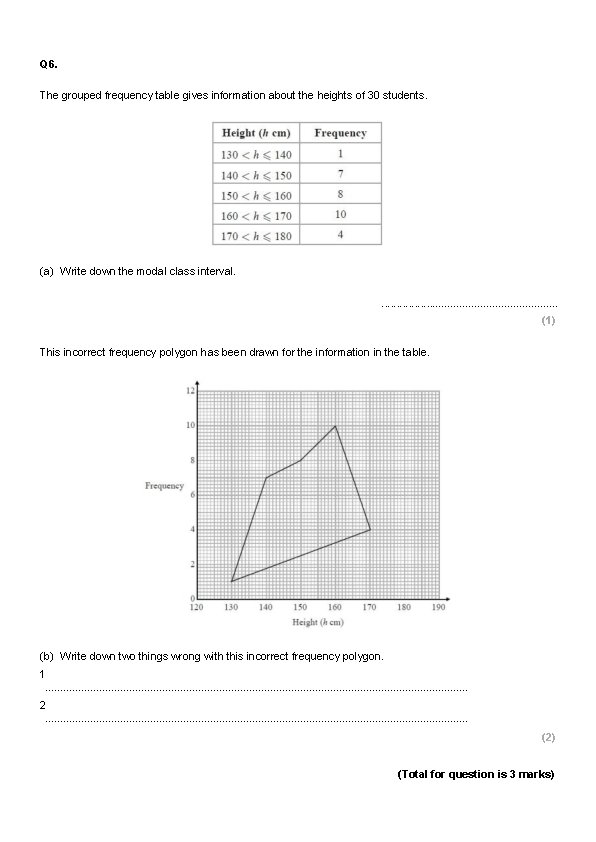
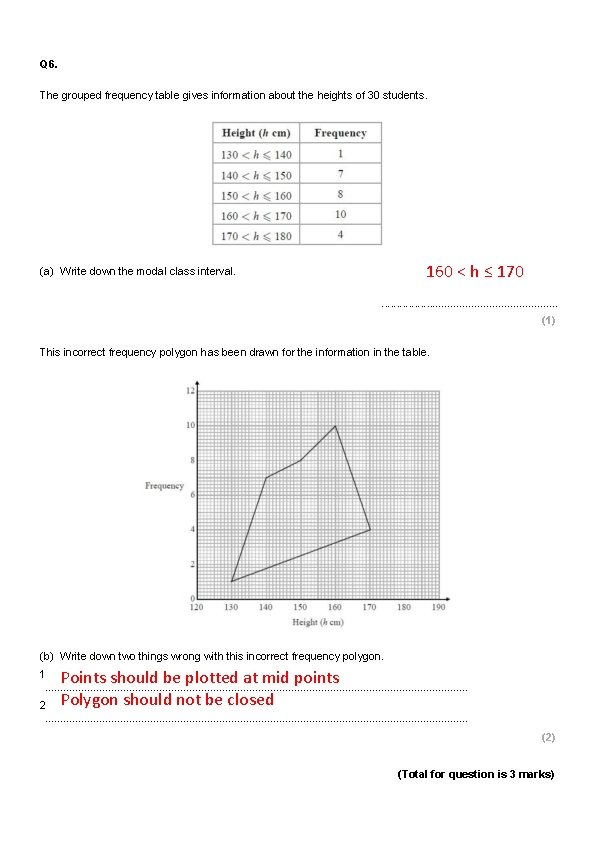
Q 6. The grouped frequency table gives information about the heights of 30 students. (a) Write down the modal class interval. . . . (1) This incorrect frequency polygon has been drawn for the information in the table. (b) Write down two things wrong with this incorrect frequency polygon. 1. . . . . . . . . 2. . . . . . . . . (2) (Total for question is 3 marks)

Q 6. The grouped frequency table gives information about the heights of 30 students. 160 < h ≤ 170 (a) Write down the modal class interval. . . . (1) This incorrect frequency polygon has been drawn for the information in the table. (b) Write down two things wrong with this incorrect frequency polygon. Points should be plotted at mid points Polygon should not be closed 1. . . . . . . . . 2. . . . . . . . . (2) (Total for question is 3 marks)

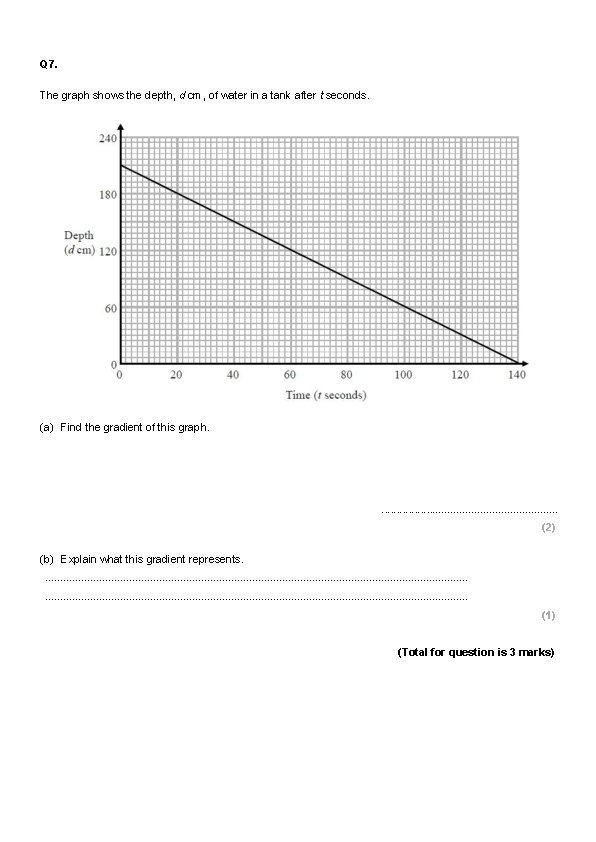
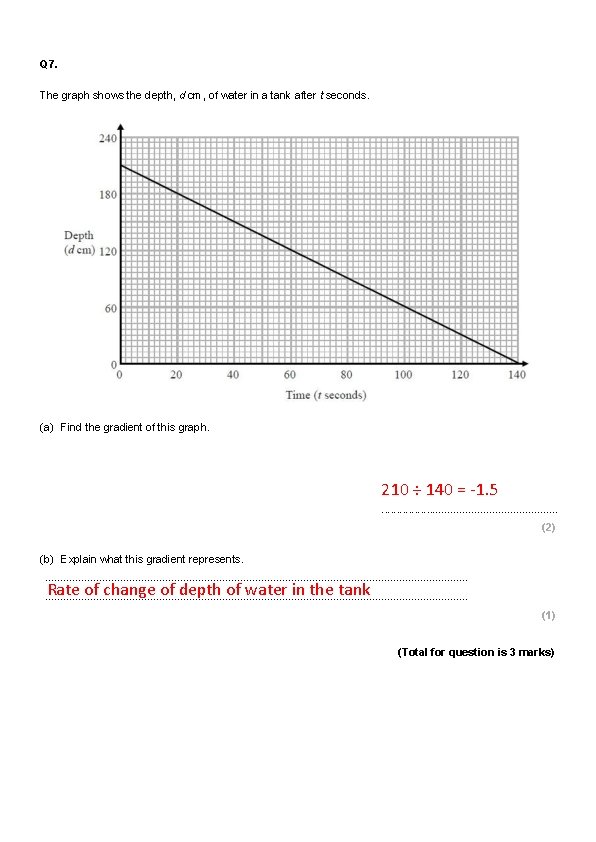
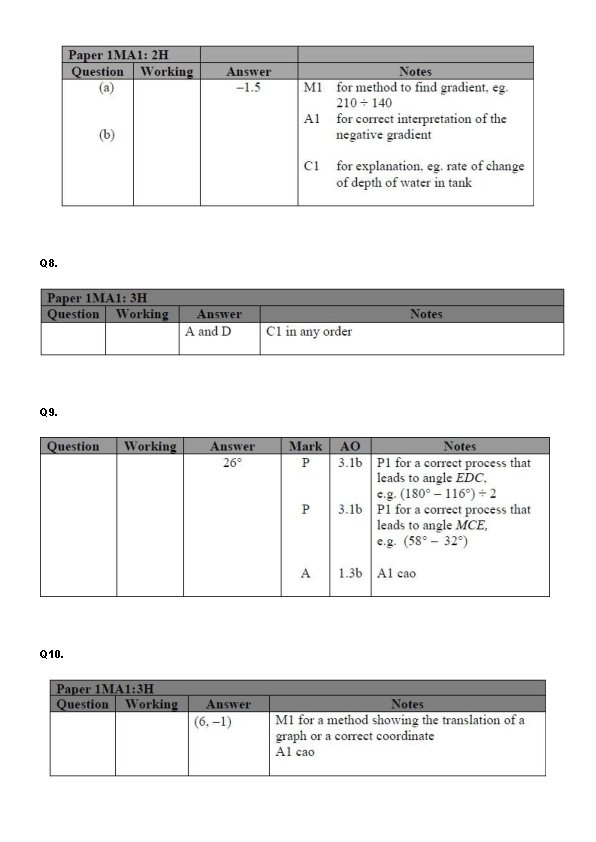
Q 7. The graph shows the depth, d cm, of water in a tank after t seconds. (a) Find the gradient of this graph. . . . (2) (b) Explain what this gradient represents. . . . . . . . . . . . . . . . . . (1) (Total for question is 3 marks)

Q 7. The graph shows the depth, d cm, of water in a tank after t seconds. (a) Find the gradient of this graph. 210 ÷ 140 = -1. 5 . . . . (2) (b) Explain what this gradient represents. . . . . . . . . Rate of change of depth of water in the tank . . . . . . . . . (1) (Total for question is 3 marks)

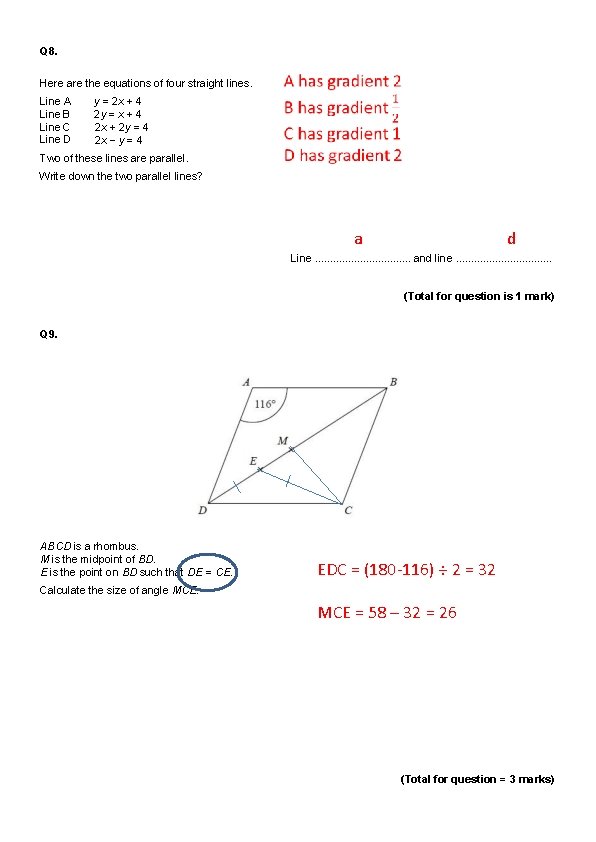
Q 8. Here are the equations of four straight lines. Line A Line B Line C Line D y = 2 x + 4 2 y = x + 4 2 x + 2 y = 4 2 x − y = 4 Two of these lines are parallel. Write down the two parallel lines? Line. . . . and line. . . . (Total for question is 1 mark) Q 9. ABCD is a rhombus. M is the midpoint of BD. E is the point on BD such that DE = CE. Calculate the size of angle MCE. (Total for question = 3 marks)

Q 8. Here are the equations of four straight lines. Line A Line B Line C Line D y = 2 x + 4 2 y = x + 4 2 x + 2 y = 4 2 x − y = 4 Two of these lines are parallel. Write down the two parallel lines? a d Line. . . . and line. . . . (Total for question is 1 mark) Q 9. ABCD is a rhombus. M is the midpoint of BD. E is the point on BD such that DE = CE. EDC = (180 -116) ÷ 2 = 32 Calculate the size of angle MCE = 58 – 32 = 26 (Total for question = 3 marks)

Q 10. The graph of y = f(x) is transformed to give the graph of y = −f(x + 3) The point A on the graph of y = f(x) is mapped to the point P on the graph of y = −f(x + 3) The coordinates of point A are (9, 1) Find the coordinates of point P. (. . . . , . . . . ) (Total for question is 2 marks) Q 11. Simplify fully (√a + √ 4 b)(√a – 2√b) . . . . (Total for question = 3 marks)

Q 10. The graph of y = f(x) is transformed to give the graph of y = −f(x + 3) The point A on the graph of y = f(x) is mapped to the point P on the graph of y = −f(x + 3) The coordinates of point A are (9, 1) Find the coordinates of point P. 9 -3 =6 because of f(x+3) 1 becomes -1 because of –f(x) 6 -1 (. . . . , . . . . ) (Total for question is 2 marks) Q 11. Simplify fully (√a + √ 4 b)(√a – 2√b) a – 2 √a√b+ √ 4 b√a - √ 4 b 2√b a - 2 √a √b + 2 √a √b -2 √b 2√b a – 4 b. . . . (Total for question = 3 marks)

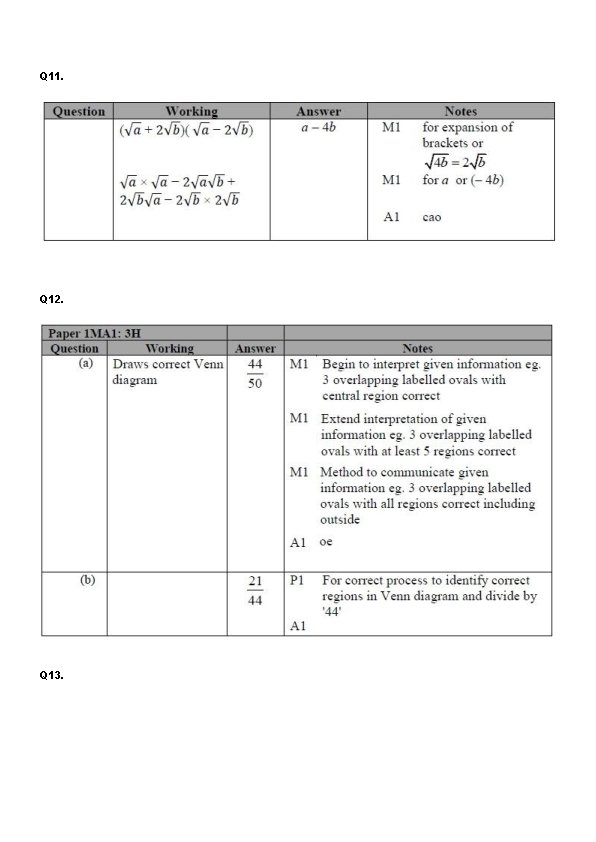
Q 12. Sami asked 50 people which drinks they liked from tea, coffee and milk. All 50 people like at least one of the drinks 19 people like all three drinks. 16 people like tea and coffee but do not like milk. 21 people like coffee and milk. 24 people like tea and milk. 40 people like coffee. 1 person likes only milk. Sami selects at random one of the 50 people. (a) Work out the probability that this person likes tea. . . . (4) (b) Given that the person selected at random from the 50 people likes tea, find the probability that this person also likes exactly one other drink. . . . (2) (Total for question = 6 marks)

Q 12. Sami asked 50 people which drinks they liked from tea, coffee and milk. All 50 people like at least one of the drinks 19 people like all three drinks. 16 people like tea and coffee but do not like milk. 21 people like coffee and milk. 24 people like tea and milk. 40 people like coffee. 1 person likes only milk. t c 4 Sami selects at random one of the 50 people. 5 (a) Work out the probability that this person likes tea. 21 -19 = 2 24 – 19 = 5 5+19+2+16+3+1 = 46 50 – 46 = 4 4+5+19+16 = 44 16 3 19 2 1 m . . . . (4) (b) Given that the person selected at random from the 50 people likes tea, find the probability that this person also likes exactly one other drink. 5 + 16 = 21 . . . . (2) (Total for question = 6 marks)

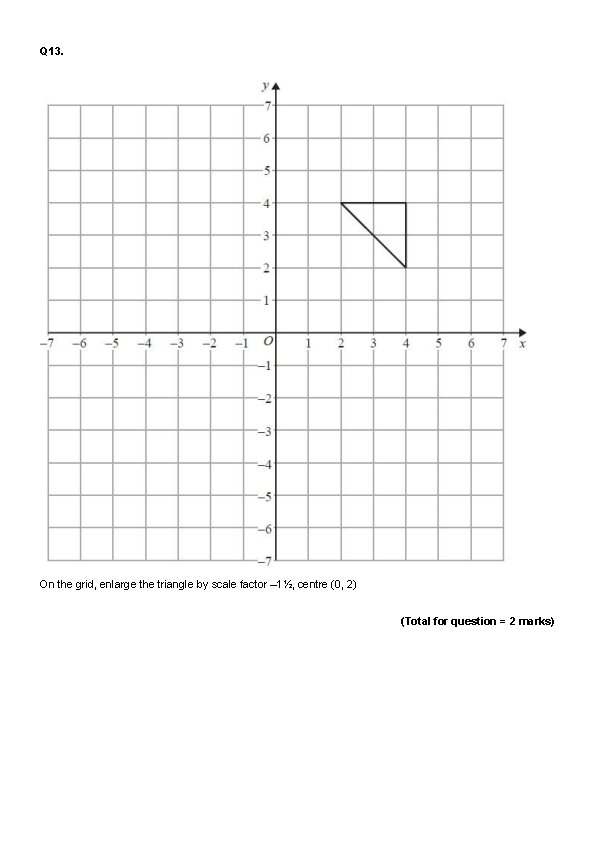
Q 13. On the grid, enlarge the triangle by scale factor – 1½, centre (0, 2) (Total for question = 2 marks)

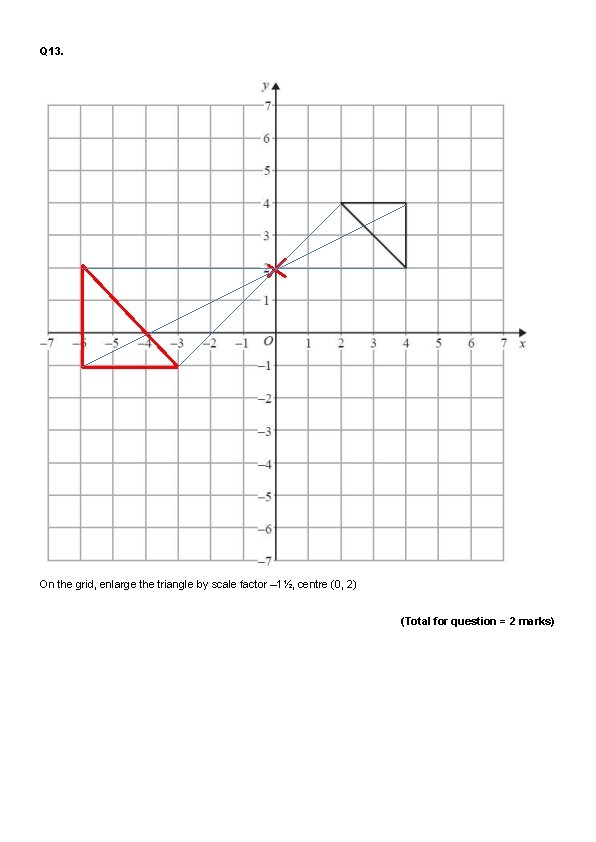
Q 13. On the grid, enlarge the triangle by scale factor – 1½, centre (0, 2) (Total for question = 2 marks)

Q 14. Solve x 2 − 5 x + 3 = 0 Give your solutions correct to 3 significant figures. . . . (Total for question = 3 marks) Q 15. (a) Show that the equation 3 x 2 − x 3 + 3 = 0 can be rearranged to give (2) (b) Using find the values of x 1, x 2 and x 3 . . . . (3) (c) Explain what the values of x 1, x 2 and x 3 represent. . . . . . . . . . . . . . . . . . (1) (Total for question is 6 marks)

Q 14. Solve x 2 − 5 x + 3 = 0 Give your solutions correct to 3 significant figures. 4. 30 or 0. 697 . . . . (Total for question = 3 marks) Q 15. (a) Show that the equation 3 x 2 − x 3 + 3 = 0 can be rearranged to give (2) (b) Using find the values of x 1, x 2 and x 3 x₁ = 3. 29296875 x₂ = 3. 276659786 x₃ = 3. 279420685 3. 28. . . . (3) (c) Explain what the values of x 1, x 2 and x 3 represent. . . . . . . . . iteration is an estimate of the solution like trial and error . . . . . . . . . (1) (Total for question is 6 marks)

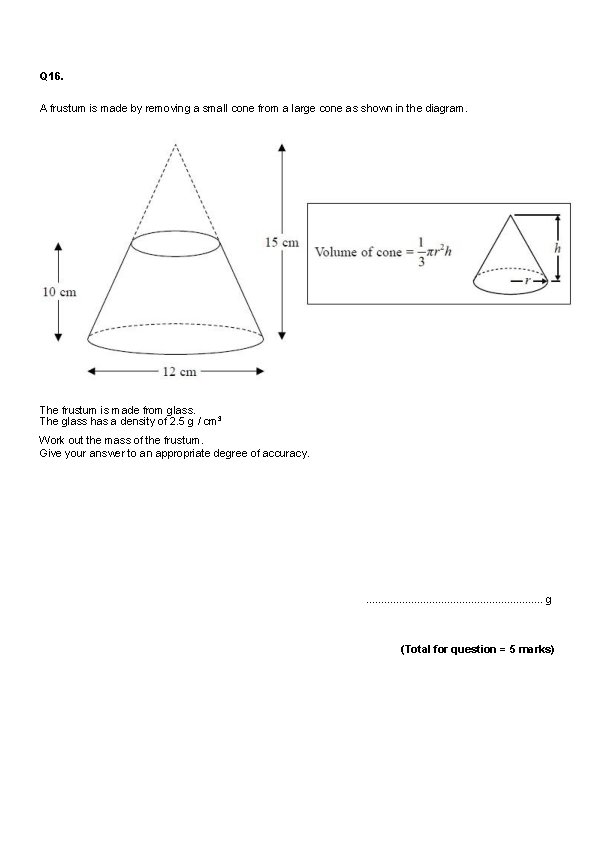
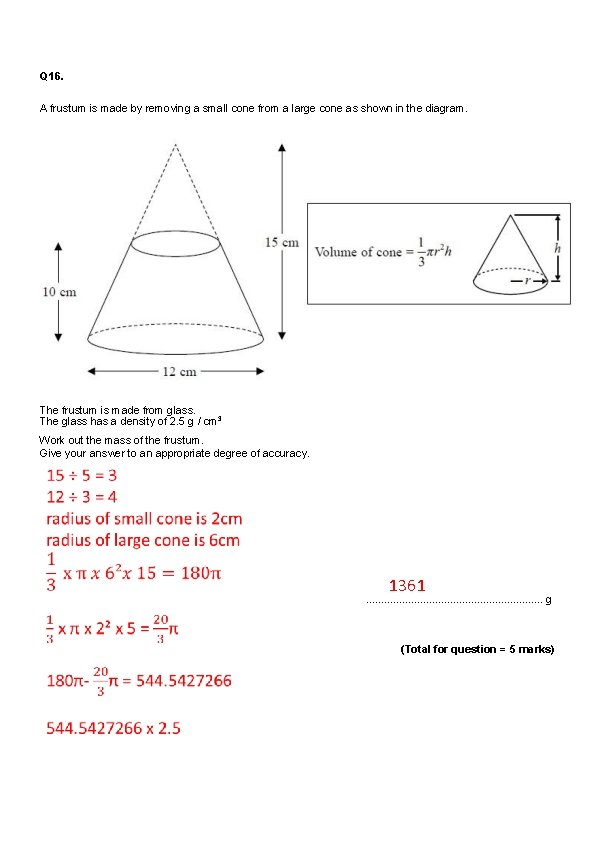
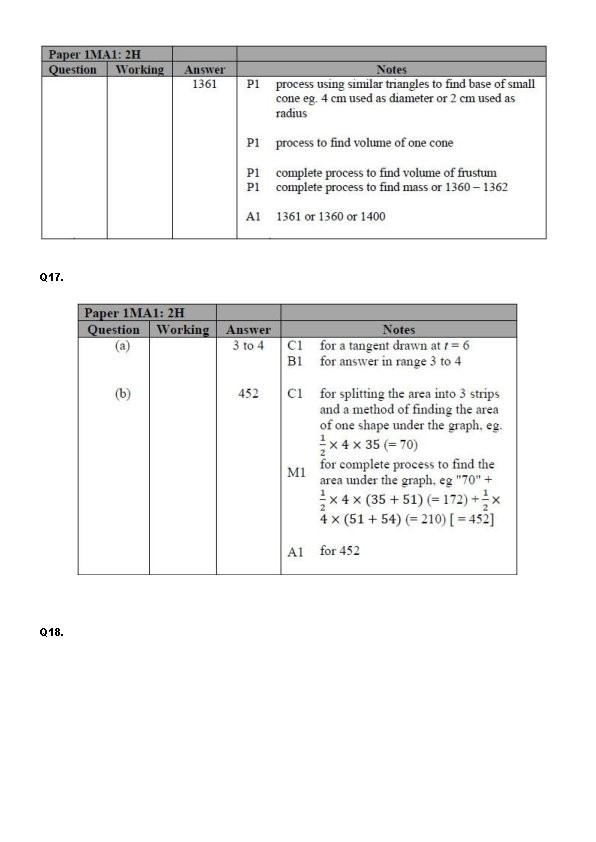
Q 16. A frustum is made by removing a small cone from a large cone as shown in the diagram. The frustum is made from glass. The glass has a density of 2. 5 g / cm 3 Work out the mass of the frustum. Give your answer to an appropriate degree of accuracy. . . . g (Total for question = 5 marks)

Q 16. A frustum is made by removing a small cone from a large cone as shown in the diagram. The frustum is made from glass. The glass has a density of 2. 5 g / cm 3 Work out the mass of the frustum. Give your answer to an appropriate degree of accuracy. 1361 . . . . g (Total for question = 5 marks)

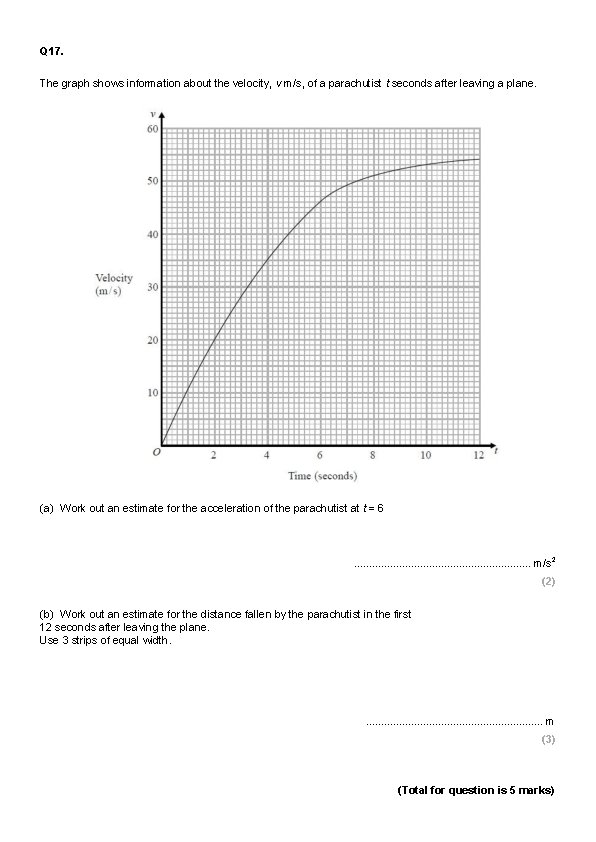
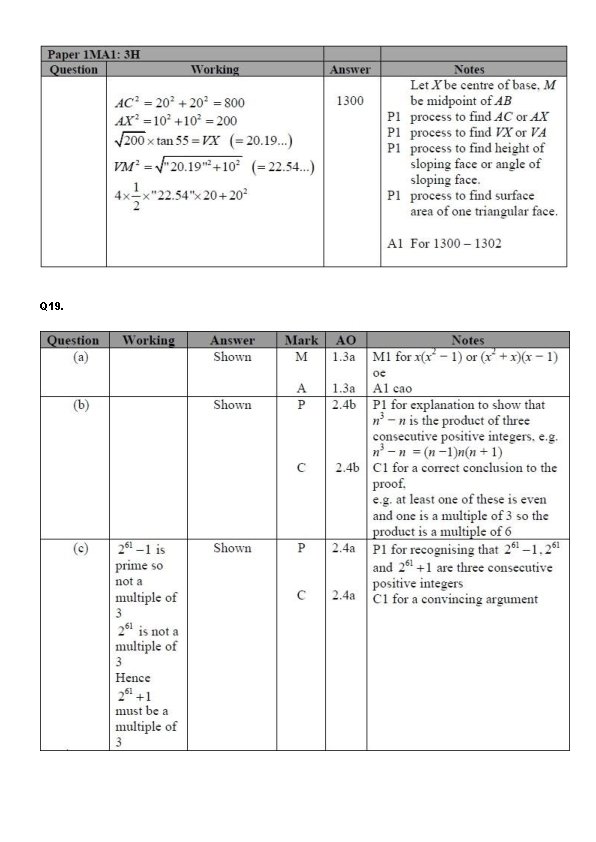
Q 17. The graph shows information about the velocity, v m/s, of a parachutist t seconds after leaving a plane. (a) Work out an estimate for the acceleration of the parachutist at t = 6 . . . . m/s 2 (2) (b) Work out an estimate for the distance fallen by the parachutist in the first 12 seconds after leaving the plane. Use 3 strips of equal width. . . . m (3) (Total for question is 5 marks)

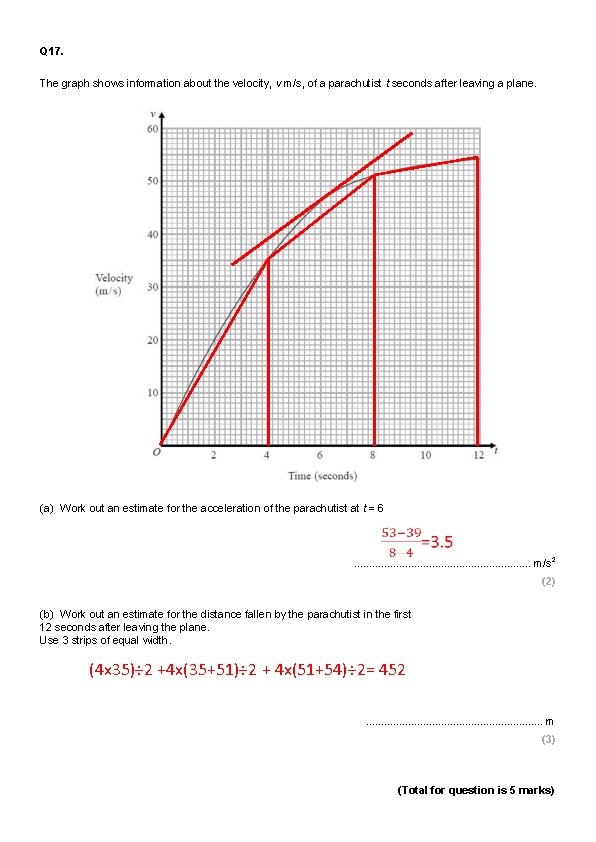
Q 17. The graph shows information about the velocity, v m/s, of a parachutist t seconds after leaving a plane. (a) Work out an estimate for the acceleration of the parachutist at t = 6 . . . . m/s 2 (2) (b) Work out an estimate for the distance fallen by the parachutist in the first 12 seconds after leaving the plane. Use 3 strips of equal width. (4 x 35)÷ 2 +4 x(35+51)÷ 2 + 4 x(51+54)÷ 2= 452 . . . . m (3) (Total for question is 5 marks)

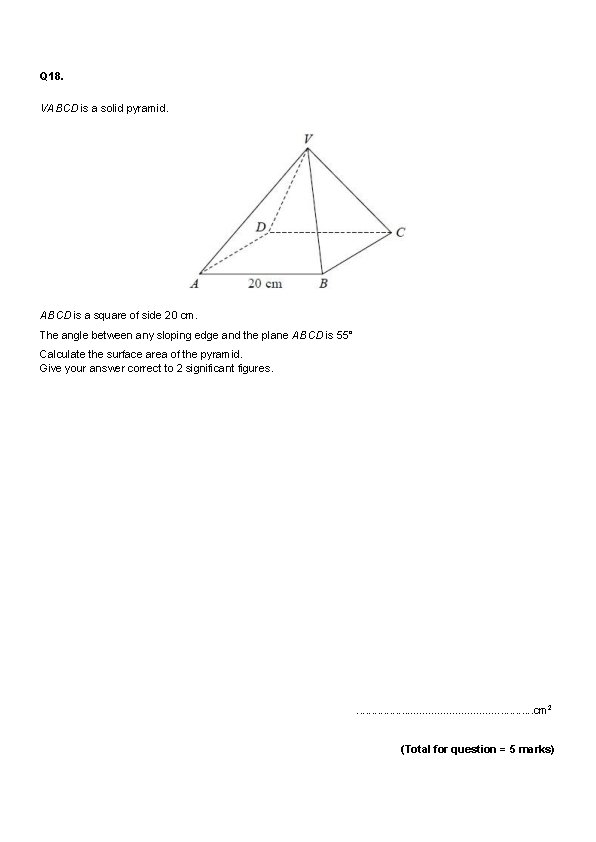
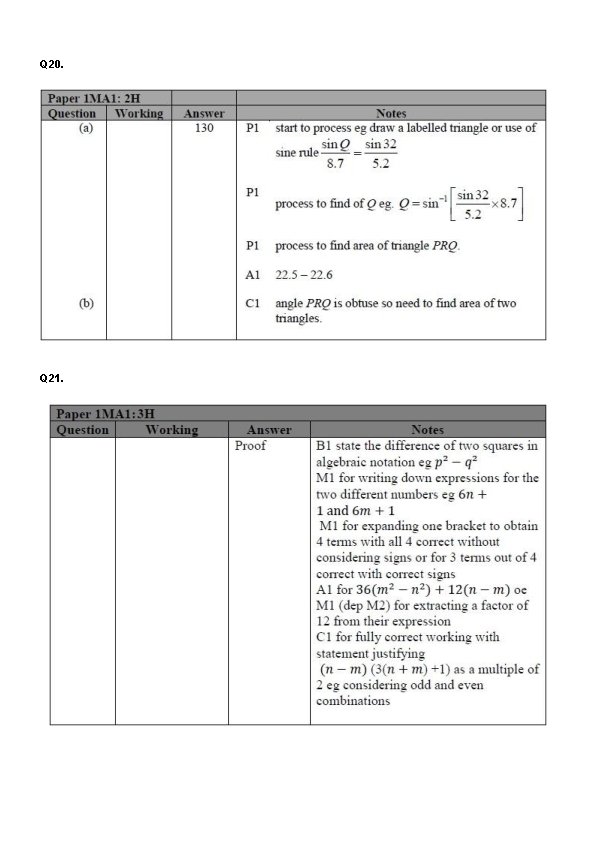
Q 18. VABCD is a solid pyramid. ABCD is a square of side 20 cm. The angle between any sloping edge and the plane ABCD is 55° Calculate the surface area of the pyramid. Give your answer correct to 2 significant figures. . . . cm 2 (Total for question = 5 marks)

Q 18. VABCD is a solid pyramid. ABCD is a square of side 20 cm. The angle between any sloping edge and the plane ABCD is 55° Calculate the surface area of the pyramid. Give your answer correct to 2 significant figures. 1300 . . . . cm 2 (Total for question = 5 marks)

Q 19. (a) Expand simplify x(x + 1)(x − 1) (2) In a list of three consecutive positive integers at least one of the numbers is even and one of the numbers is a multiple of 3 n is a positive integer greater than 1 (b) Prove that n 3 − n is a multiple of 6 for all possible values of n. (2) 261 − 1 is a prime number. (c) Explain why 261 + 1 is a multiple of 3 (2) (Total for question = 6 marks)

Q 19. (a) Expand simplify x(x + 1)(x − 1) x (x²-1) x³-x (2) In a list of three consecutive positive integers at least one of the numbers is even and one of the numbers is a multiple of 3 n is a positive integer greater than 1 (b) Prove that n 3 − n is a multiple of 6 for all possible values of n. (n-1)n(n+1)=(n²-n)(n+1)=n³-n²+n²-n=n³-n n-1 and n+1 are consecutive numbers If middle one is even the next one or previous one would be a multiple of three therefore a multiple of 6 (2) 261 − 1 is a prime number. (c) Explain why 261 + 1 is a multiple of 3 261 − 1 , 261 and 261 +1 These are 3 consecutive numbers the first is odd as all prime numbers are odd except 2 so the next is even so the next is a (2) multiple of 3 (Total for question = 6 marks)

Q 20. In triangle RPQ, RP = 8. 7 cm PQ = 5. 2 cm Angle PRQ = 32° (a) Assuming that angle PQR is an acute angle, calculate the area of triangle RPQ. Give your answer correct to 3 significant figures. . . . cm 2 (4) (b) If you did not know that angle PQR is an acute angle, what effect would this have on your calculation of the area of triangle RPQ? . . . . . . . . . . . . . . . . . (1) (Total for question = 5 marks) Q 21. Here are the first five terms of an arithmetic sequence. 7 13 19 25 31 Prove that the difference between the squares of any two terms of the sequence is always a multiple of 24 (Total for question is 6 marks)

Q 20. In triangle RPQ, RP = 8. 7 cm PQ = 5. 2 cm Angle PRQ = 32° (a) Assuming that angle PQR is an acute angle, calculate the area of triangle RPQ. Give your answer correct to 3 significant figures. . . . cm 2 (4) (b) If you did not know that angle PQR is an acute angle, what effect would this have on your calculation of the area of triangle RPQ? . . . . . . . . . If it were obtuse you would need to find the area of 2 triangles . . . . . . . . . (1) (Total for question = 5 marks) Q 21. Here are the first five terms of an arithmetic sequence. 7 13 19 25 31 Prove that the difference between the squares of any two terms of the sequence is always a multiple of 24 (Total for question is 6 marks)

Mark Scheme Q 1. Q 2. Q 3. Q 4.

Q 5. Q 6. Q 7.

Q 8. Q 9. Q 10.

Q 11. Q 12. Q 13.

Q 14. Q 15. Q 16.

Q 17. Q 18.

Q 19.

Q 20. Q 21.
 Name date class teacher
Name date class teacher Name, class, subject
Name, class, subject Name teacher class date
Name teacher class date Predicted outcome value theory
Predicted outcome value theory Desired service and adequate service
Desired service and adequate service Dividend declaration date
Dividend declaration date Dividend eligibility
Dividend eligibility Calculating infusion time and completion time
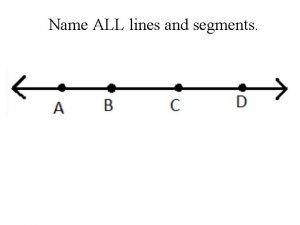
Calculating infusion time and completion time Name three lines
Name three lines Wave function calculator higher maths
Wave function calculator higher maths Higher history paper 2
Higher history paper 2 Higher english mrs midas past paper
Higher english mrs midas past paper Advanced higher biology unit 2
Advanced higher biology unit 2 Start time, end time and elapsed time
Start time, end time and elapsed time Name class date
Name class date Name title date
Name title date Name date period
Name date period Speaker title
Speaker title Name title date
Name title date The giver utopia project examples
The giver utopia project examples By name title date
By name title date Session title examples
Session title examples By name title date
By name title date Name title date
Name title date By name title date
By name title date By name title date
By name title date By name title date
By name title date By name title date
By name title date By name title
By name title By name title date
By name title date Name class teacher date
Name class teacher date Name title date
Name title date Name class teacher date
Name class teacher date Name title date
Name title date Name title date
Name title date Name date period
Name date period Name date class
Name date class Cs 391
Cs 391 Name title date
Name title date Desirable weight
Desirable weight