nalisis de lgoritmos Tomado de la Universidad Nacional

nalisis de lgoritmos Tomado de la Universidad Nacional Sede Bogota Depto. De Sistemas

OUTLINE v Recurrences • Examples of recurrences and the Iteration method • Characteristic equation method • Substitution method • Recursion tree method • Master method • Z transform

EXAMPLES OF RECURRENCES INCREMENTAL RECURRENCES: • Min • Insertion Sort DIVIDE AND CONQUER RECURRENCES: • Chip Testing Problem • Binary Search • Convex Hull

INCREMENTAL RECURRENCES Min Insertion Sort

General form T(n-1)+f(n) for n 1 0 for n =0 T(n)=

Iteration Method T(n) = T(n-1) + f(n) = T(n-2) + f(n-1) + f(n) : = T(0) +f(1) +f(2)+ … + f(n-1) + f(n) T(n)=

Min T(n)= T(n-1)+ 1 = =n Insertion sort T(n)= T(n-1)+(n-1) = = n(n-1)/2

Arithmetic Series T(n) = T(n-1) + ( n-1 ) f(i)=i -1 S= n(n -1)/2 S = 1 + 2 + 3 +. . . + (n-1) S = (n-1)+(n -2)+(n -3)+. . . + 1 2 S = n + n +. . . + n {n-1 terms}

Geometric Series f(i)=a ri-1 S= -S = -a - ar 2 -. . . - arn-1 r. S = + ar 2 +. . . + arn-1 + arn (r-1)S= -a+ arn If r is a constant bounded away from 1 then S is approximately a constant times the largest term in the series.

Mixed Series f(i)= iri S =

-S = -1 r 1 -2 r 2 - … - nrn r. S = 1 r 2+. . . + (n-1)rn + nrn+1 (r-1)S = - (r + r 2 +. . . + rn) + nrn+1 (r-1)S = - r(1+ r+. . . + rn-1) + nrn+1 S

DIVIDE AND CONQUER Chip Testing Problem

This problem is motivated by the VLSI industry, where millions of VLSI chips must be tested for defaults. The idea is to let the chips test each other by built-in circuitry. Note that VLSI stands for very large scale integration which is the integrated-circuit chip technology used to fabricate most microprocessors today. There are two kinds of chips - good and bad. Good chips always tell the truth, i. e. will report accurately whether the tested chip is good or bad. Bad chips say anything about the other chip, thus cannot be trusted. Our goal is to identify all good chips. The problem must be solved in O(n) ) time.

It is assumed that there are more good chips than bad. In other words, |G| > |B|. Our computational model states that each chip tested counts for one time unit. It suffices to define one good chip in time O(n). This is because one good chip can identify all good chips in O(n) time

A naive method We are going to test each chip individually by comparing it against all remaining chips. We take votes from the remaining chips and let the majority decide. In case of equality, good wins. If a chip is declared bad, it is junked and we continue. Time Analysis : (n-1)+(n-2)+(n-3)+. . . +(n/2) n +. . + n = (n 2)/2 = O(n 2) However such time is unacceptable, for it greatly exceeds O(n) time.

Divide and conquer Definitions : · G : set of all good chips · B : set of all bad chips · B-B : pair of chips that has been declared "bad, bad" · B-G : pair of chips that has been declared "bad, good" · G-G : pair of chips that has been declared "good, good"

Iteration: If n = 1 or n = 2, then return one chip (it is good). If n is odd, test odd chip. If odd chip is good, return the chip (it is good). If odd chip is bad, with remaining chips do : · pair all chips · junk all B-G, B-B pairs · junk one chip of every G-G pair · find (recursively) one good chip among the remaining chips

Correctness If before the iteration, |G| > |B|, then after the iteration, |G| > |B|. Before the pairing step, we have |G| |B| + 2. Each B-B, B-G pair has at one bad chip. So we junk at least as many bad chips as good ones obtaining G 1 and B 1. So, we still have |G 1| |B 1| + 2.

Each G-G pair has either two good chips or two bad ones; what matters is that both chips are alike. Thus, the halving step leaves us with G 2 = G 1 /2, B 2 = B 1 /2. So, we still have |G 1| /2 |B 1|/2 + 2 /2 , |G 2| |B 2| + 1. Then before the next iteration |G| |B| + 1.

Time complexity If T(n) is the worst-case time for n chips, then T(2) = T(1) = 0 and T(n) n - 1 + n/2 + T( n/2 ) < 3 n/2 + T(n/2 ) Then T(n) 3 n/2 + T(n/2 )

Iteration Method T(n) 3 n/2 + T(n/2 ) 3 n/2 + 3 n/4 + T(n/4 ) 3 n/2 + 3 n/4 + 3 n/8 + T(n/8 ). . . So that clearly T(n) 3 n/2 (1 + 1/2 + 1/4 + 1/8 +. . . ) = 3 n = O(n)

Applet from http: //www. cs. mcgill. ca/~cs 251/Old. Courses/1997

Binary Search

We are searching for a value x in a sorted array A[1. . n] of size n. We examine the middle value. Either this is the value we are looking for and we are done, or we must search for the value in either the left or the right half of the table. Thus we obtain a smaller problem of the same type as we had before (which we can solve recursively).

Binary search strategy (bisection method) Find out if x is equal, larger or smaller than an/2 x = an/2 A A x < an/2 x > an/2 x = an/4 x < an/4 x > an/2 Discarded x = an/8 A Discarded :

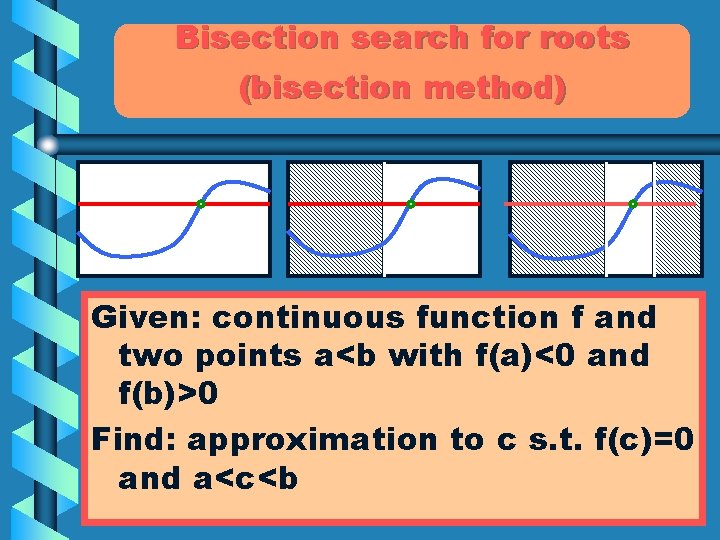
Bisection search for roots (bisection method) Given: continuous function f and two points a<b with f(a)<0 and f(b)>0 Find: approximation to c s. t. f(c)=0 and a<c<b

The recurrence we obtain is T(n) T( n/2 ) + 1

Iteration Method n=2 k, k = lg n T(n) = T( n/2 ) + 1 = 1+1+ T( n/4 ) = (1+1+ …+1) = O(lg n) k = lg n

for general n T(n) T( n/2 ) + 1 1+1+ T( n/4 ) (1+1+ …+1) lg n So that clearly T(n) = O(lg n)

Convex Hull

Convex Hull, CH(X), is the smallest convex polygon containing all points from X, |X|=n X “It is similar to placing a rubber band around the set and letting go! “

The following algorithm to find a convexhull uses a divide and conquer method similar to merge-sort: Convex. Hull(A) B= Convex. Hull (first half of A) C= Convex. Hull (second half of A) Merge. Convex. Hull(B, C) divide-and-conquer divides into two subsets left and right in O(n), then combine into one convex hull in O(n).

The recurrence we obtain is T(n) 2 T( n/2 ) + O(n)

The Towers of Hanoi

The Legend It is said that after creating the world, God set on Earth three rods made of diamond and 64 rings of gold. These rings are all of different size. At the creation they were threaded on one of the rods in order of size, the largest at the bottom and the smallest at the top. God also created a monastery close to the rods. The monk´s task in life is transfer all the rings onto another rod. The only operation permitted is to move one single disk form one rod to another, in such way that no ring is ever placed on top of another smaller one. When the monks finish their task the monastery will turn to dust and the world will come to an end.

Hanoi(n, i, j) if (n > 0) then Hanoi(n-1, i, 6 -i-j) move i ® j Hanoi(n-1, 6 -i-j, j) end_if

The recurrence we obtain is T(n) = 2 T(n-1 ) + 1

Applet from http: //www. mazeworks. com/hanoi/

CHARACTERISTIC EQUATION METHOD

Linear Homogeneous Difference Equations antn + an-1 tn-1 + an-2 tn-2+ … + an-k tn-k =0 with k initial conditions t 0= l 0 , t 1= l 1 , … , tk-1= lk-1 Guess that tn is of the form n therefore we must have (characteristic equation) an n + an-1 + an-2 n-2+ … + an-k =0 an k + an-1 k-1+ an-2 k-2+ … + ak =0

Let be = r 1 , r 2 , …. , rk the roots of the characteristic equation (all different). Then tn = rin is a solution and a linear combination of the rin is also a solution The constants ci are determined by the initial conditions. Fact: !the difference equation has only solutions of this form!

Examples Fibonacci: tn = tn-1 + tn-2 for n 2, t 0 = 0, t 1 = 1 Guess that xn is of the form n therefore must have n= n-1+ n-2 i. e. 2 - - 1=0 (characteristic eqn. ) tn= A +B

Solve for n=0 and 1 to find A and B • n=0: A+B = 0 = t 0 • n=1: ((A+B)+(A-B) )/2 = 1 = t 1 Therefore A = 1/ B =-1/ Then tn = 1/

Second example tn- 3 tn-1 - 4 tn-2 = 0 for n 2, t 0 = 0, t 1 = 1 2 - 3 - 4 = 0 (characteristic eqn. ) 1= -1, 2= 4 tn= A(-1)n + B(4)n

Solve for n=0 and 1 to find A and B • n=0: A + B = t 0 = 0 • n=1: -A + 4 B = t 1 =1 Therefore A = -1/5 B = 1/5 Then tn = 1/ 5 ((4)n - (-1)n ).

Third example tn= tn-1 - tn-2 for n 2, t 0 = 0, t 1 = 1 2 - + 1 = 0 (characteristic eqn. ) 1, 2 = = tn= A +B

Solve for n=0 and 1 to find A and B • n=0: A + B = t 0 = 0 • n=1: A +B = t 1 =1 Therefore A = 1/ B = -1/ tn = 2 / sin(n / 3) is periodic: 0, 1, 1, 0, -1, -1, . . .

Roots with multiplicity > 1 If ri is a root with multiplicity 2 of of the characteristic equation p( ) = ak k + ak-1 + … + a 1 1 + a 0 h( ) = [ n-k p( ) ]’ = ak n n + ak-1 (n-1) n-1 + … + a 0 n-k

Let assume p( ) = ( - r)2 q( ) h( ) = [ n-k p( ) ]’ = [ n-k ( - r)2 q( )]’ = [ ( - r)2 n-k q( )]’ = [2 ( - r) n-k q( ) +( - r)2 [ n-k q( )]’ ] = ak n n + ak-1 (n-1) n-1 + … + a 0 n-k Then h(r) =0 and tn = nrin is a solution of the diff. equ.

In general, if ri is a root with multiplicity m of of the characteristic equation. Then tn = nrin, tn = n 2 rin , … , tn = nm-1 rin are solutions and a linear combination of these solutions are solutions.

example tn = 5 tn-1 - 8 tn-2 + 4 tn-3 for n 3, t 0 = 0, t 1 = 1 , t 2 = 2 3 - 5 2 + 8 - 4 = ( - 1)( - 2) 2 = 0 (characteristic eqn. ) 1= 1, 2= 2 tn= A(1)n + B(2)n+ Cn(2)n

A+B =0 A + 2 B + 2 C = 1 A + 4 B + 8 C = 3 A = -2 B=2 C = - 1/2 tn= -2(1)n + 2(2)n - (1/2)n(2)n = 2 n+1 - n 2 n-1 - 2

Linear Inhomogeneous Difference Equations antn + an-1 tn-1 + 2+ … + ak tn-k = b np(n) with b constant, p(n) polynomial of degree d and k initial conditions t 0= p 0 , t 1= p 1 , … , tk-1= pk-1. Has the solutions obtained form the char. equ. (an n + an-1 + … + ak) (t-b) d+1 = 0

example tn - 2 tn-1 = 3 n Multiplying by 3: 3 tn - 6 tn-1 = 3 n+1 Replace n by n+1: tn+1 - 2 tn- = 3 n+1 Subtracting: tn+1 - 5 tn- + 6 tn-1 = 0 Char. Equ. : 2 - 5 + 6 = ( - 2)( - 3) = 0 tn= A(2)n + B(3)n

Hanoi example tn = 2 tn-1 + 1 char. equ. : ( - 2)( - 1) = 0 tn= A(2)n + B(1)n • t 0 = 0 • t 1 = 1 A+ B = 0 2 A+ B = 1 tn= 2 n - 1

Change of variables example T(n) = 4 T(n/2) + n Replace n by 2 k T(2 k) = 4 T(2 k-1) + 2 k call tk- = T(2 k) then T(2 k) = 4 T(2 k-1) + 2 k is tk = 4 tk-1 + 2 k

Char. equ. : ( - 4)( - 2) = 0 tk= C 1(4)k + C 2 2 k Back in n, 2 k = n, 4 k = (22)k = (2 k)2 = n 2 tk = T(2 k) = T(n) then T(n)=C 1 n 2 + C 2 n

Second example T(n) = a. T(n/b) + nh (cd lgdn + cd-1 lgd-1 n + c 0 ) Replace n by bk T(bk) = a. T(bk-1) + ( bh )k (cd kd + cd-1 kd+ c 0 ) call tk- = T(2 k) then tk - atk-1 =( bh )k (cd kd + cd-1 kd+ c 0 )

char. equ. : ( - a)( - bh) d+1 = 0 tk= C 1(a)k + D 0 (bh)k + D 1 k(bh) k + D 2 k 2(bh) k + D 3 k 3(bh) k + …. + Dd kd(bh) k Back in n, bk = n, ak = (bk)logba then T(n) = C 1 n logba + D 0 nh + D 1 logbn nh + D 2 log 2 bn nh + … + Dd logdbn nh

SUBSTITUTION METHOD

Steps • Guessing the form of the solutions, then using mathematical induction to find the constants and show the solution works. • It works well when it is easy to guess. But, there is no general way to guess the correct solution.

Example Solve: Guess: Proof: T(n) = 3 T( n/3 ) + n T(n) = O(n lg n), i. e. T(n) = cn lg n T(n) = 3 T( n/3 ) + n T(n) 3 c n/3 lg n/3 + n c n lg (n/3) + n = c n lg n - c n lg 3 + n = c n lg n - n (c lg 3 - 1) c n lg n * The last step is true for c 1 / lg 3.

Making a Good Guess • Guessing a similar solution to the one that you have seen before – T(n) = 3 T( n/3 + 5) + n similar to – T(n) = 3 T( n/3 ) + n when n is large, the difference between n/3 and (n/3 + 5) is insignificant

• Another way is to prove loose upper and lower bounds on recurrence and then reduce the range of uncertainty. Start with T(n) = (n) & T(n) = O(n 2) T(n) = (n log n)

Subtleties When the math doesn’t quite work out in the induction, try to adjust your guess with a lower-order term. For example: We guess T(n) O(n) for T(n) = 3 T( n/3 )+ 4, but we have T(n) 3 c n/3 + 4 = c n + 4

New guess is T(n) c n - b, where b 0 3(c n/3 - b)+4 = c n - 3 b + 4 = c n - b - (2 b-4) Therefore, T(n) c n - b, if 2 b - 4 0 or if b 2

Change of Variables Use algebraic manipulation to turn an unknown recurrence similar to what you have seen before. Consider T(n) = 2 T( n 1/2 ) + lg n Rename m = lg n and we have T(2 m) = 2 T(2 m/2) + m

S(m) Set S(m) = T(2 m) and we have = 2 S(m/2) + m S(m) = O(m lg m) Changing back from S(m) to T(n), we have T(n) = T(2 m) = S(m) = O(m lg m) = O(lg n lg lg n)

Avoiding Pitfalls • Be careful not to misuse asymptotic notation. For example: – We can falsely prove T(n) = O(n) by guessing T(n) c n for T(n) = 2 T( n/2 ) + n T(n) 2 c n/2 + n cn+n = O(n) Wrong! – The err is that we haven’t proved T(n) c n

MASTER THEOREM FOR DIVIDE AND CONQUER RECURRENCE

Master Theorem Let a 1, b>1 be constants, f(n) be a function and T(n) defined by T(n)=a. T(n/b)+f(n) then • if for >0 then T(n) = (n logba )

• if f(n) = (n logba ) then T(n) = (n logba * lg n) • if f(n) = (n logba + ) for >0 and if a(f(n/b)) cn for c < 1 and all sufficiently large n then

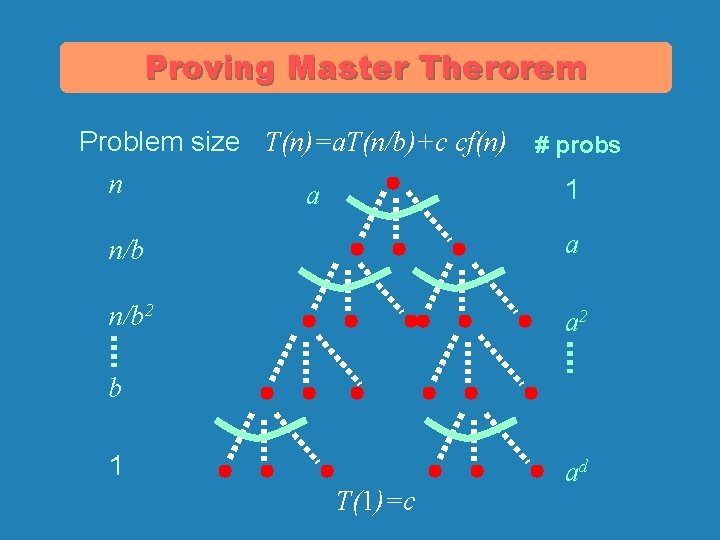
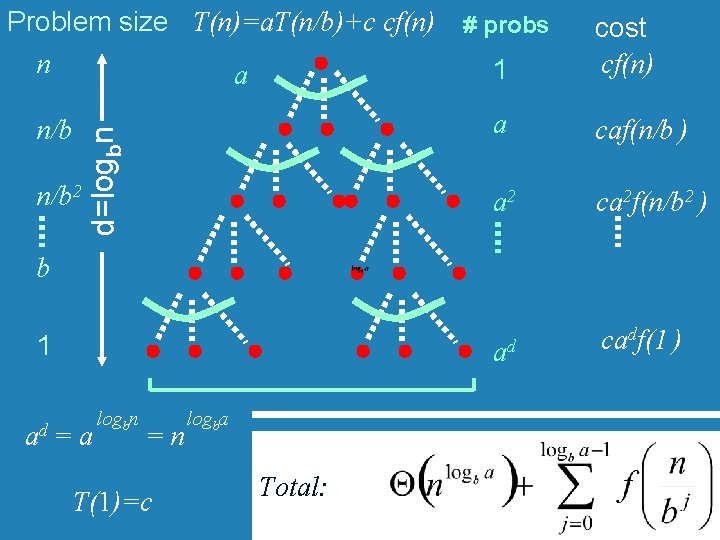
Proving Master Therorem Problem size T(n)=a. T(n/b)+c cf(n) # probs n 1 a n/b 2 a 2 b 1 T(1)=c ad

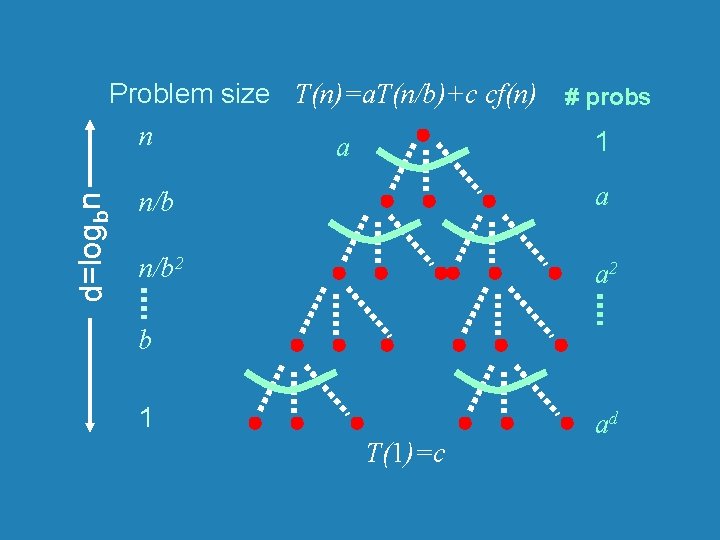
d=logbn Problem size T(n)=a. T(n/b)+c cf(n) # probs n 1 a n/b 2 a 2 b 1 T(1)=c ad

n/b 2 d=logbn Problem size T(n)=a. T(n/b)+c cf(n) # probs n 1 a cost cf(n) a caf(n/b ) a 2 ca 2 f(n/b 2 ) ad cadf(1 ) b 1 ad = a logbn =n T(1)=c logba Total:

Lemma Let a 1, b>1 be constants, f(n) be a nonnegative defined on exact powers of b. A function g(n) defined on exact powers of b by

Can then be bounded asymptotically for exact powers of b as follows • if then for >0

• if then • if for >0 and if a(f(n/b)) cn for c < 1 and all sufficiently large n then

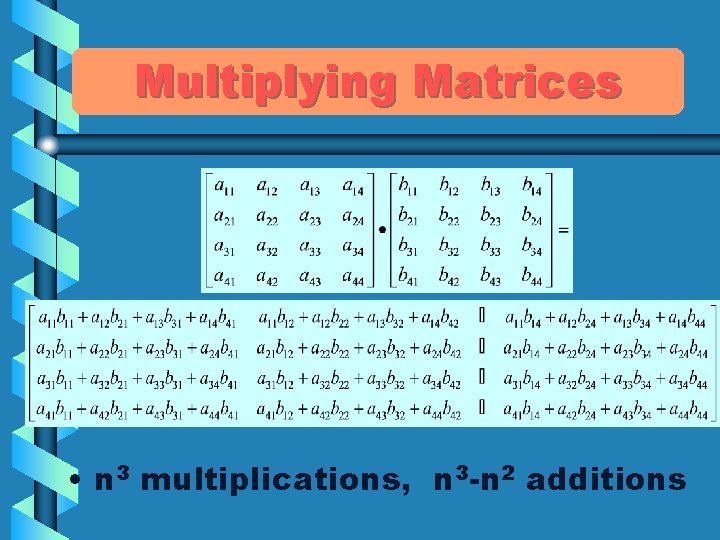
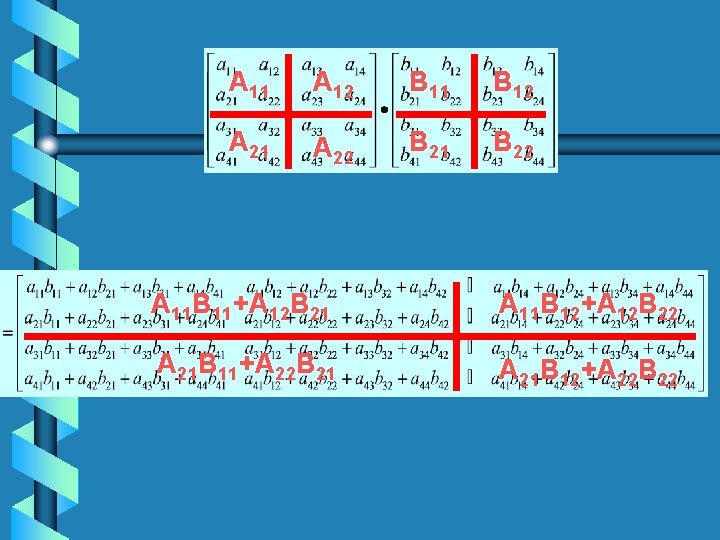
Multiplying Matrices • n 3 multiplications, n 3 -n 2 additions

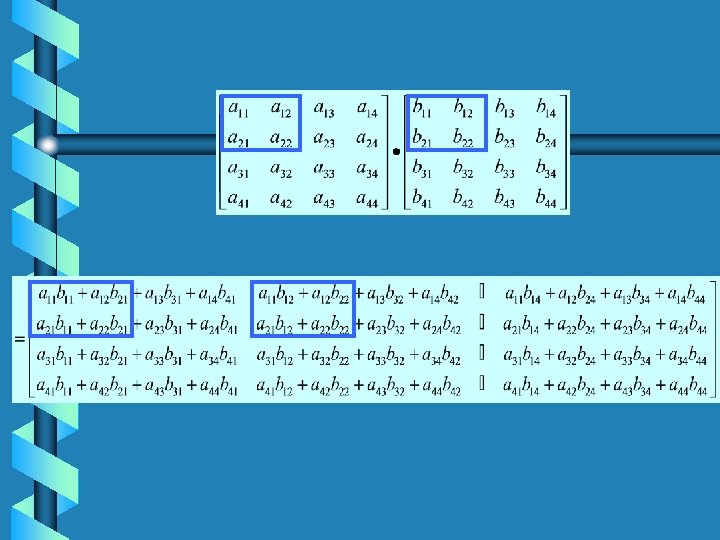
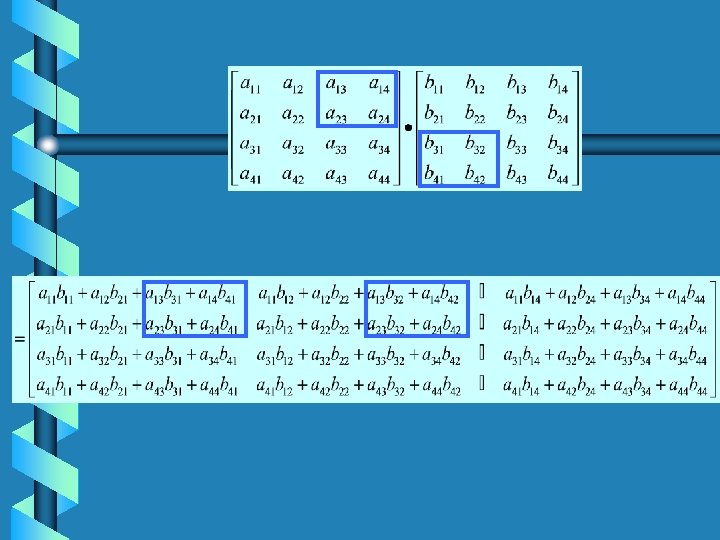
A 11 A 12 B 11 B 12 A 21 A 22 B 21 B 22 A 11 B 11+A 12 B 21 A 11 B 12+A 12 B 22 A 21 B 11+A 22 B 21 A 21 B 12+A 22 B 22

= A 11 A 12 B 11 B 12 A 21 A 22 B 21 B 22 A 11 B 11+A 12 B 21 A 11 B 12+A 12 B 22 A 21 B 11+A 22 B 21 A 21 B 12+A 22 B 22 • T(n)=8 T(n/2)+4(n/2)2=8 T(n/2)+n 2 8>22 so T(n) is

Exercises • Solution of T(n) = T( n/2 ) + 1 is O(lg n) • Solution of T(n) = 2 T( n/2 + 17) + n is O(n lg n) • Solve T(n) = 2 T(n 1/2) + 1 by making a change of variables. Don’t worry whether values are integral.