NAF Conversion An Efficient Solution for the Range

NAF Conversion: An Efficient Solution for the Range Matching Problem in Packet Filters 1 AUTHOR: NIZAR BEN NEJI, ADEL BOUHOULA PUBLISHER: IEEE INTERNATIONAL CONFERENCE , 2011 PRESENTER: KAI-YANG LIU DATE: 2011/08/31

Introduction 2 The cause of the coexistence of range based and prefix based fields within the filtering rules. In this paper, we deal with prefix-based solutions. The available solutions usually require that the filtering rules must be written only in prefix format. Arbitrary ranges need to be usually converted into standard prefixes when dealing with prefix based solutions.

Direct Range to Prefix Conversion 3

Exmaple 4

Direct Range to Prefix Conversion 5 In the worst case, the w-bit range [1, 2 w− 2] is split into 2 w− 2 prefixes. For example, the 4 -bit worst case range [1, 14] requires 6 prefixes as follows:

Non-Adjacent Form 6 Every integer n has a unique non-adjacent form (NAF). NAF is a signed binary representation (SBR) of length k and of the form n = where the digits are in {− 1, 0, 1} satisfying the property that ai×ai+1 = 0 Example: 47 is 101111 = 32+8+4+2+1 and the NAF form is

Proposed Technique 7 Notations and Terminology: 1. w is the size of the packet header field to be inspected. 2. A w-bit range R = [l , u]satisfies 0 ≤ l ≤ 2 w− 1 (lower bound) and 0 ≤u ≤ 2 w − 1 (upper bound) where l ≤ u.

Proposed Technique 8 3. Adjacent ranges: Two w-bit ranges [l 1 , u 1] and [l 2 , u 2] are adjacent if l 2 = u 1+1. 4. Consecutive elementary ranges: Two elementary ranges[l 1 , u 1] and [l 2 , u 2] are consecutive if they are adjacent and they have same widths or consecutive power of 2 widths. => |width 1−width 2| = min(width 1 , width 2)

Conversion Algorithm of a Single Range 9 Lower{ } is a list of Integers and it stores lower bounds of ranges, Upper{ } is a list of Integers and it stores upper bounds of ranges, Sign{ } is a binary list and it stores signs as 0 s and 1 s, the zero value means “＋” and one means “－”.

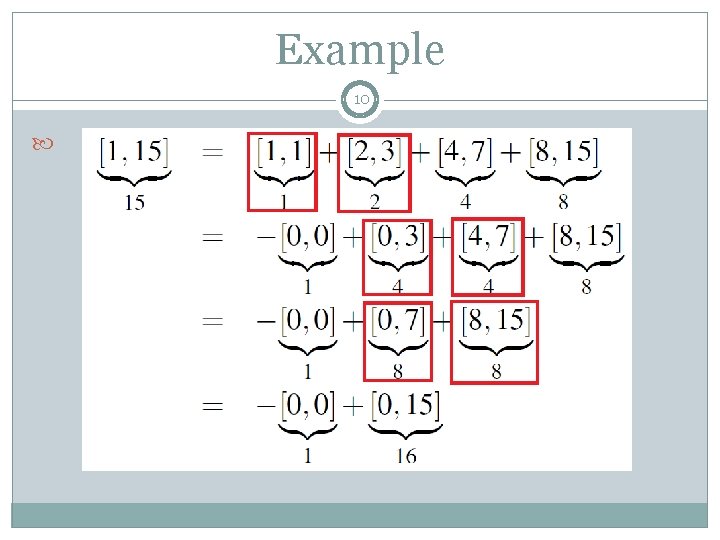
Example 10

Example 11 Case 1: difference equals to zero Ex: [4, 7] , [8, 11] [4, 7] = 01** [8, 11] = 10** U 1+1=L 2 , L 2=(1000)2 max(width 1, width 2)=4 => L 2 mod (2. max(midth 1, width 2))=0 ∴ can’t be converted

Example 12 Case 2: difference equals to width 1 Ex: [6, 7] , [8, 11] [6, 7] = 011* [8, 11] = 10** U 1+1=L 2 , L 2=(1000)2 max(width 1, width 2)=4 => L 2 mod (2. max(midth 1, width 2))=0 ∴ can’t be converted

Matching Algorithm 13 Two main phases: searching for the longest matching prefix and then searching for the shortest prefix that doesn’t match. Ex: A. 2 = (0010)2 B. 4 = (0100)2.

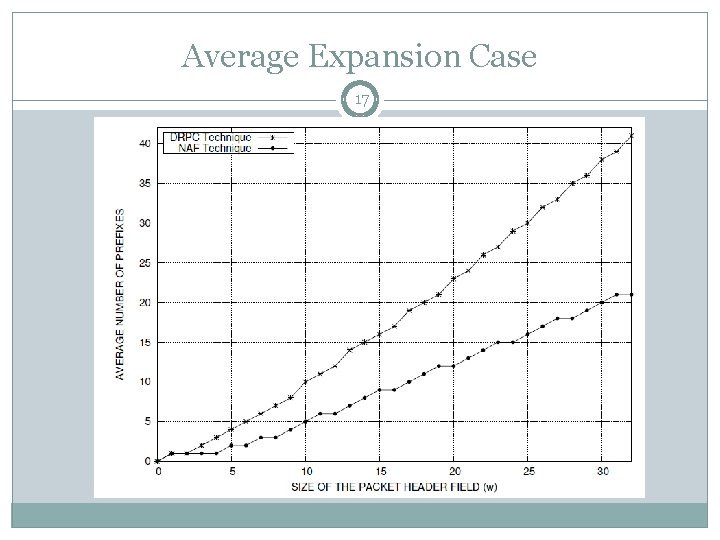
Performance Analysis 14 Worst Expansion Case The worst expansion case for DRPC algorithm gives for the w-bit range of the form [1, 2 w− 2] 2 w-2 prefixes. The proposed algorithm: → Only 3 prefixes

The Worst Case for the NAF Conversion 15 The worst case expansion is only w prefixes Example:

General Case of the Worst Result 16

Average Expansion Case 17

Special Cases 18 Converting multiple ranges: 1. Two intersecting ranges [a , b] and [c , d] and c≤b 2. Two disjoint ranges such that b+1<c Left and right extremal ranges: Left: [0, a ] with 0≤a≤ 2 W-1 ；Worst: [0, 2 W-2] Right: [b, 2 W-1 ] with 0≤b≤ 2 W-1 ；Worst: [1, 2 W-1]

Special Cases 19 Negation of an arbitrary range: The negation of the w-bit range [a, b] gives two extremal w-bit ranges [0, a− 1] and [b+1, 2 w− 1]. Worst case of DRPC : 2 w-2 prefixes given by the range of the form Worst case of NAF conversion : w prefixes given by the negation of the range of the form: