NA 4 Domain Decomposition Develop a MATLAB code

(NA 4) Domain Decomposition: Develop a MATLAB code which solve a nonlinear ode BVP using domain decomposition. start by learn how to use parfor Matlab command. Sec: 11. 3 parfor i = 1: n commands; end Finite-Difference Methods for Linear Problems Example boundary-value problem Equations at interfaces

(NA 5) Newton-type methods with cubic convergence: Develop a MATLAB code which finds roots of a function. Start by reading the first three pages of the this paper "Homeier, H. H. H. "On Newton-type methods with cubic convergence. " Journal of computational and applied mathematics 176. 2 (2005): 425432. " Newton method by approximating the integral by trapezoidal approximation Potra and Pták Frontini and Sormani considered the midpoint rule Weerakoon and Fernando rederived the Newton method

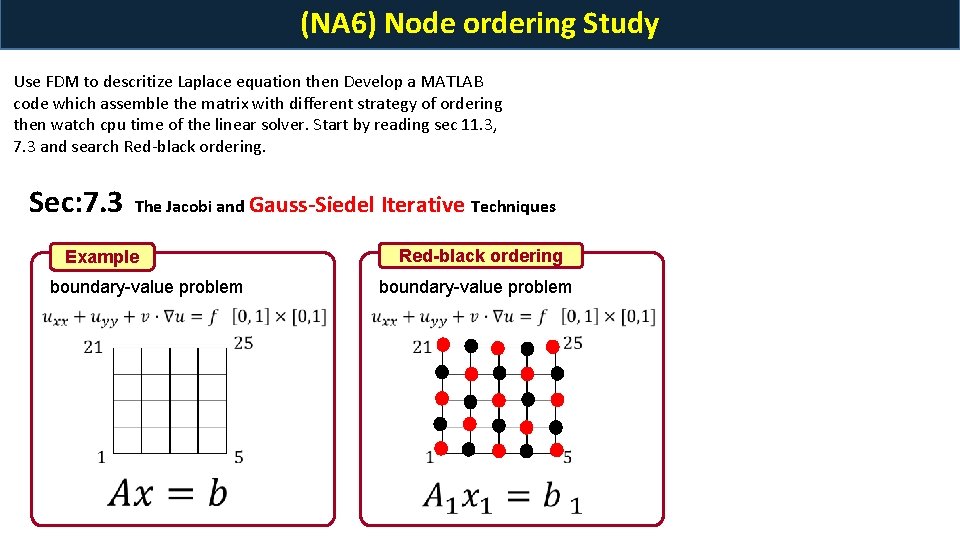
(NA 6) Node ordering Study Use FDM to descritize Laplace equation then Develop a MATLAB code which assemble the matrix with different strategy of ordering then watch cpu time of the linear solver. Start by reading sec 11. 3, 7. 3 and search Red-black ordering. Sec: 7. 3 The Jacobi and Gauss-Siedel Example boundary-value problem Iterative Techniques Red-black ordering boundary-value problem

(NA 7) Chebfun for Darcy's equation: Use Chebfun to solve 1 D Darcy-Forchheimer equation. Start by getting the equation from “A Block. Centered Finite Difference Method For The Darcy–Forchheimer Model” by Hongxing Rui and Hao Pan, SIAM J. Numer. Anal. vol. 50, no. 5, pp. 2612– 2631" then solve it by chebfun. some links https: //en. wikipedia. org/wiki/Chebfun http: //www. chebfun. org/docs/guide 10. html DARCY FORCHHEIMER Nick Trefethen Chebfun is a system written in MATLAB that looks and feels like MATLAB, except that vectors and matrices become functions and operators. Whenever MATLAB has a discrete command, Chebfun aims to have the same command overloaded to execute a continuous analogue. For example, SUM(f) gives you the integral of a chebfun f over its interval of definition

(NA 13) Preconditioning Technique Use Finite difference methods to solve 2 ed or 4 th order ode using two different scheme one with low order and the second with high order. Use the low order scheme matrix as a preconditioner to solve the linear system generated by the high order scheme. Start by reading sec 11. 3 and search for preconditioning linear system or see these slides. Sec: 11. 3 Finite-Difference Methods for Linear Problems Example high order scheme Preconditioned linear system boundary-value problem low order scheme Faster convergence (less number of iterations)

(NA 1) Multigrid Method Develop a MATLAB code which solve a linear 4 th order BVP using two-grid method. Start by reading section 7. 3 and iterative refinement in 7. 5. You may consult the slides in here or A Multigrid Tutorial, Second Edition. Coarse Mesh Sec: 11. 3 Finite-Difference Methods for Linear Problems Example boundary-value problem high order scheme Fine Mesh

(NA 1) Multigrid Method Two-Grid Cycle Algorithm Remark: 1) few GS iterations on the system Given an approximate: to obtain an approximate solution We want to improve this approximate: Pre-smoothing step 2) Compute the residual (residual) (error) 3) Restrict the residual 4) Solve residual equation on coarse mesh 5) Interpolate Restriction step Prolo. Correctio n step Prolongation step 6) Update 7) few GS iterations on the system With initial approximate Post-smoothing step

(NA 9) Numerical Comparison Study for RK and chepfun in chemical eng Select an IVP in chemical eng and solve it using RK and Chebfun. some links https: //en. wikipedia. org/wiki/Chebfun http: //www. chebfun. org/docs/guide 10. html if the rate of the reaction is r and if denote the concentration of compound A, . . . by CA, . . . , Nick Trefethen Chebfun is a system written in MATLAB that looks and feels like MATLAB, except that vectors and matrices become functions and operators. Whenever MATLAB has a discrete command, Chebfun aims to have the same command overloaded to execute a continuous analogue. For example, SUM(f) gives you the integral of a chebfun f over its interval of definition

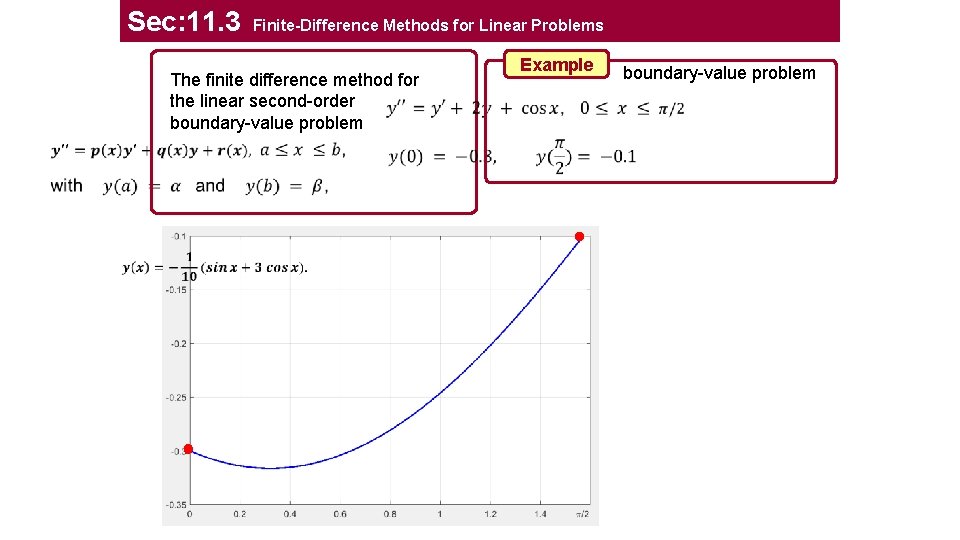
Sec: 11. 3 Finite-Difference Methods for Linear Problems The finite difference method for the linear second-order boundary-value problem Example boundary-value problem

Sec: 11. 3 Finite-Difference Methods for Linear Problems Example boundary-value problem 1 we select an integer N N=3 2 divide the interval [a, b] into (N+1) equal subintervals 3 At the interior mesh points, xi, for i = 1: N, the differential equation is approximated as ( centeral diff )

Sec: 11. 3 Finite-Difference Methods for Linear Problems Example We have the following: boundary-value problem 4 5 Write in Matrix form and solve the system

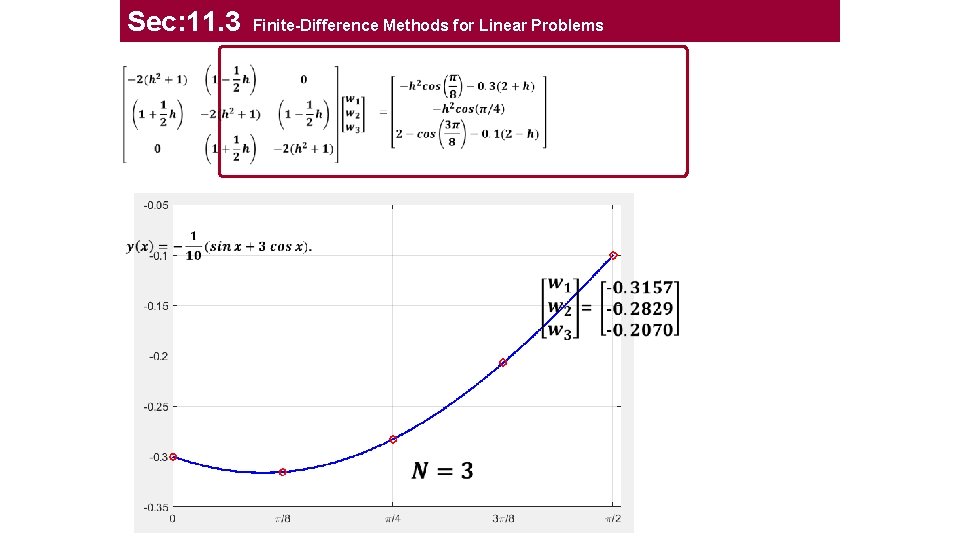
Sec: 11. 3 Finite-Difference Methods for Linear Problems Example boundary-value problem 2. 3084 -0. 8037 0 -1. 1963 2. 3084 -0. 3157 -0. 5014 -0. 1090 -0. 1394 -0. 2829 -0. 2070

Sec: 11. 3 Finite-Difference Methods for Linear Problems

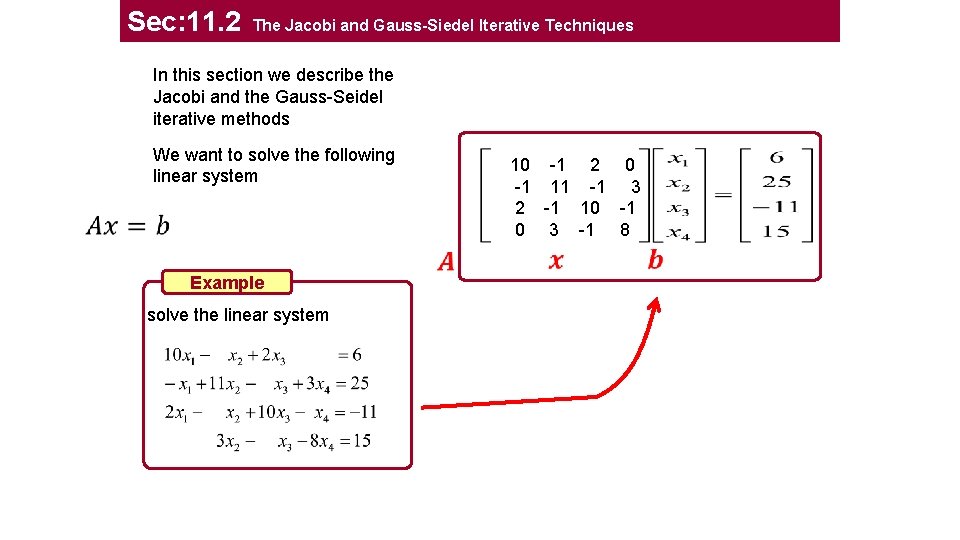
Sec: 11. 2 The Jacobi and Gauss-Siedel Iterative Techniques In this section we describe the Jacobi and the Gauss-Seidel iterative methods We want to solve the following linear system Example solve the linear system 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8

Sec: 11. 2 The Jacobi and Gauss-Siedel Iterative Techniques We want to solve the following linear system Example solve the linear system Keep the diagonal on the left hand side Jacobi Iterative Method Change the coeff of LHS to be one by division

Sec: 11. 2 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi Iterative Method

Sec: 11. 2 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi Iterative Method 0. 6000 1. 0473 0. 9326 1. 0152 0. 9890 2. 2727 1. 7159 2. 0533 1. 9537 2. 0114 -1. 1000 -0. 8052 -1. 0493 -0. 9681 -1. 0103 1. 8750 0. 8852 1. 1309 0. 9738 1. 0214 1. 0032 0. 9981 1. 0006 0. 9997 1. 0001 1. 9922 2. 0023 1. 9987 2. 0004 1. 9998 -0. 9945 -1. 0020 -0. 9990 -1. 0004 -0. 9998 0. 9944 1. 0036 0. 9989 1. 0006 0. 9998

Sec: 11. 2 The Jacobi and Gauss-Siedel Iterative Techniques Gauss Seidel Method Note that in the Jacobi iteration one does not use the most recently available information. Note that Jacobi’s method in this example required twice as many iterations for the same accuracy. 0. 6000 1. 0302 1. 0066 2. 3273 2. 0369 2. 0036 -0. 9873 -1. 0145 -1. 0025 0. 8789 0. 9843 0. 9984 1. 0009 2. 0003 -1. 0003 0. 9998 1. 0001 2. 0000 -1. 0000

Sec: 11. 2 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi iteration for general n: Gauss-Seidel iteration for general n: