n n n n Convolutional Codes Representation of

목차 n n n n Convolutional Codes Representation of Convolutional Codes Trellis Diagram Viterbi Decoder의 구조 Viterbi Decoder – Example Convolutional Encoder 설계 2

Convolutional Codes(1/7) n n 오류정정부호의 분류 1. Tree code ¨ Linear tree code n n n Linear recurrent codes Convolutional codes 2. Block code 선형부호(Linear codes) ¨ 순환부호(Cyclic code) ¨ 3

Convolutional codes(2/7) n Convolutional codes의 특징 ¨ ¨ ¨ 1955년 Elias의해 소개. Random error에 강한 특성. AWGN( Addtive White Gaussian Noise) 채널에서의 오류정정능력 우 수. 인터리버(Interleaver/Deinterleaver)를 이용하여 Burst error에 대해서 도 적용가능. 쉽게 Soft decision coding이 가능하다. n ¨ n 약 2 d. B 추가적인 coding gain을 얻을 수 있다. Easy multirate codec Implementation. Convolutional codes의 응용 ¨ Satellite communications n ¨ VSAT, INMARSAT, HDTV, MSAT, … Mobile communication, GSM, IMT-2000… n Used for most radio communication systems 4

Convolutional codes(3/7) 일반적인 통신 시스템의 구성 5

Convolutional codes(4/7) n ( n, k, m) Convolutional encoder m : 메모리 소자의 개수 ( shift registers ) ¨ k : 입력 비트 수 ¨ n : 출력 비트 수 ¨ K : 구속장(constraint length) ¨ n n 한 개의 입력 비트가 영향을 끼치는 output sequence의 길이 K = m +1 Code rate : k/n ¨ Example : ¨ n n (2, 1, 3) convolutional code k =1, n = 2, shift registers = 3, code rate = 1/2 , K = 4 6

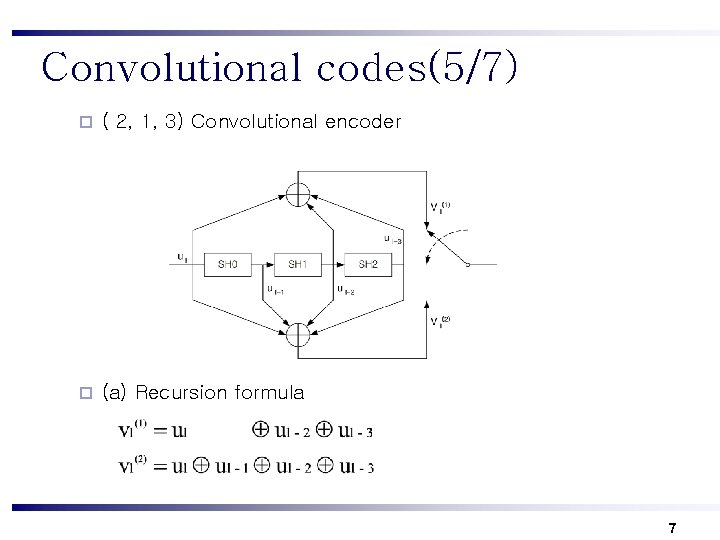
Convolutional codes(5/7) ¨ ( 2, 1, 3) Convolutional encoder ¨ (a) Recursion formula 7

Convolutional codes(6/7) ¨ ¨ Generator sequences (impulse response) Recursion formula using generator sequences ¨ Information sequence : ¨ Generator sequence : ¨ 8

Convolutional codes(7/7) ¨ Output sequence: 9

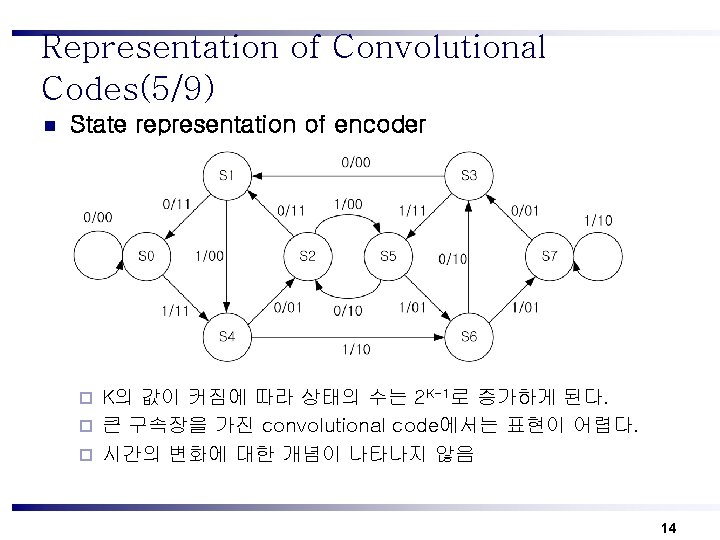
Representation of Convolutional Codes(1/9) ¨ Generation polynomials g(1)(D) = 1 + D 2 + D 3 g(2)(D) = 1 + D 2 + D 3 ¨ Gernerator matrix 10

Representation of Convolutional Codes(2/9) n Impulse response encoder Register contents Branch Word V 1 V 2 1000 1 1 0100 0 1 0010 1 1 0001 1 1 Input u 1 0 1 1 Module Branch Word 11 01 11 11 00 00 11 01 11 11 11 01 00 01 10 00 11 Input seq : 1000 Output seq : 11, 01, 11 11

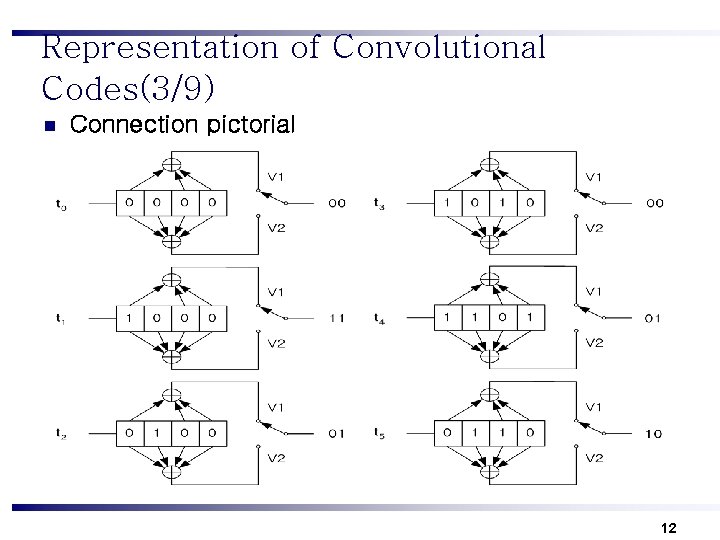
Representation of Convolutional Codes(3/9) n Connection pictorial 12

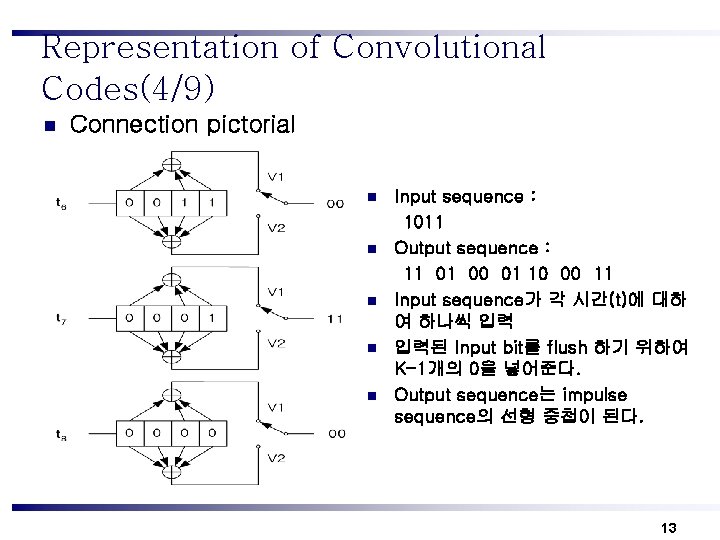
Representation of Convolutional Codes(4/9) n Connection pictorial n n n Input sequence : 1011 Output sequence : 11 01 00 01 10 00 11 Input sequence가 각 시간(t)에 대하 여 하나씩 입력 입력된 Input bit를 flush 하기 위하여 K-1개의 0을 넣어준다. Output sequence는 impulse sequence의 선형 중첩이 된다. 13

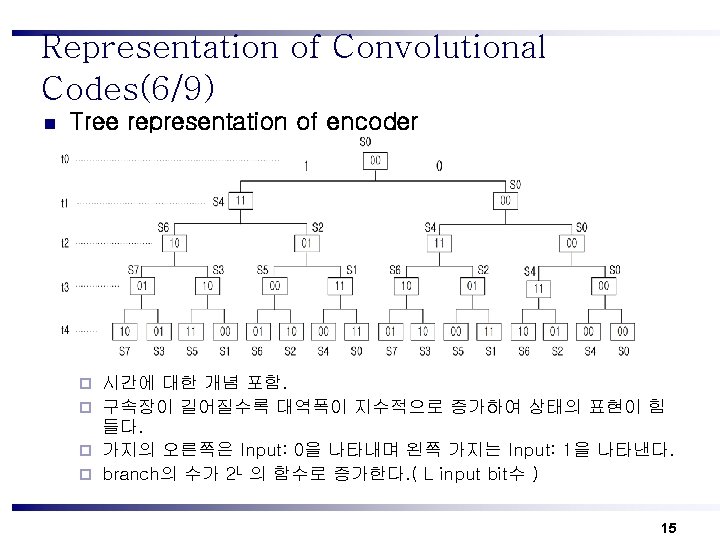
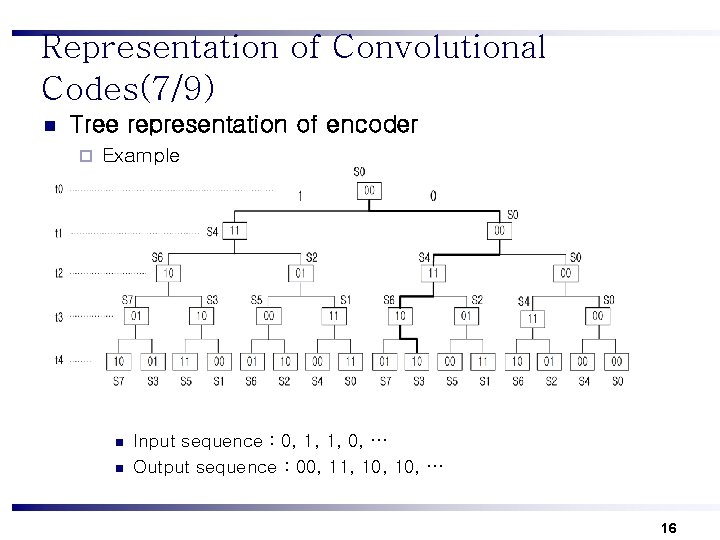
Representation of Convolutional Codes(7/9) n Tree representation of encoder ¨ Example n n Input sequence : 0, 1, 1, 0, … Output sequence : 00, 11, 10, … 16

Representation of Convolutional Codes(9/9) n Trellis diagram : butterfly structure ¨ 각각의 state는 butterfly 구조를 가지고 있다. 18

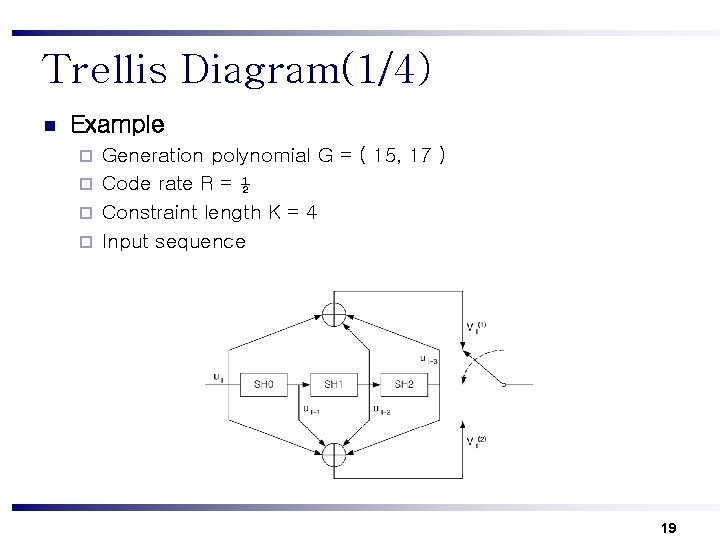
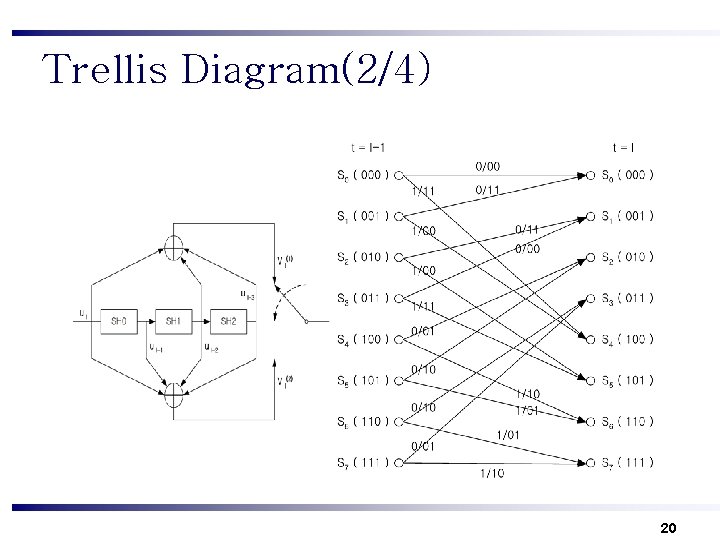
Trellis Diagram(1/4) n Example Generation polynomial G = ( 15, 17 ) ¨ Code rate R = ½ ¨ Constraint length K = 4 ¨ Input sequence ¨ 19

Trellis Diagram(2/4) 20

Trellis Diagram(4/4) Input sequence : 0, 1, 1, 0, 0, 1 … ¨ Output sequence : 00, 11, 10, 00, … ¨ 22

Catastrophic Code(1/2) ¨ # of decoding error bits -> undesirable code ) => Catastrophic code ( 23

Catastrophic Code(1/2) Generator가 최소 1차의common polynomial factor를 가지면 catastrophic error 발생 ¨ noncatastrophic code의 조건 ¨ n n ¨ For ( n, 1, m ) code Generator polynomials Example: n gcd (1 + D, 1 + D 2 ) = 1 + D => Catastrophic code 24

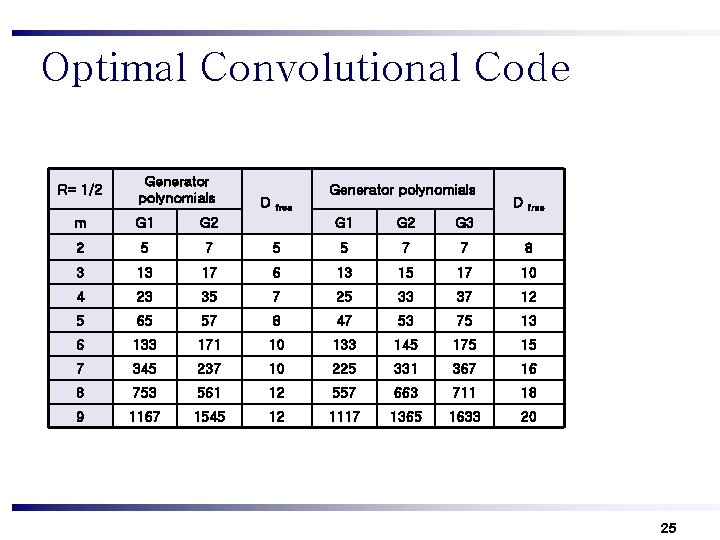
Optimal Convolutional Code R= 1/2 Generator polynomials m G 1 G 2 2 5 7 3 13 4 D Generator polynomials free D free G 1 G 2 G 3 5 5 7 7 8 17 6 13 15 17 10 23 35 7 25 33 37 12 5 65 57 8 47 53 75 13 6 133 171 10 133 145 175 15 7 345 237 10 225 331 367 16 8 753 561 12 557 663 711 18 9 1167 1545 12 1117 1365 1633 20 25

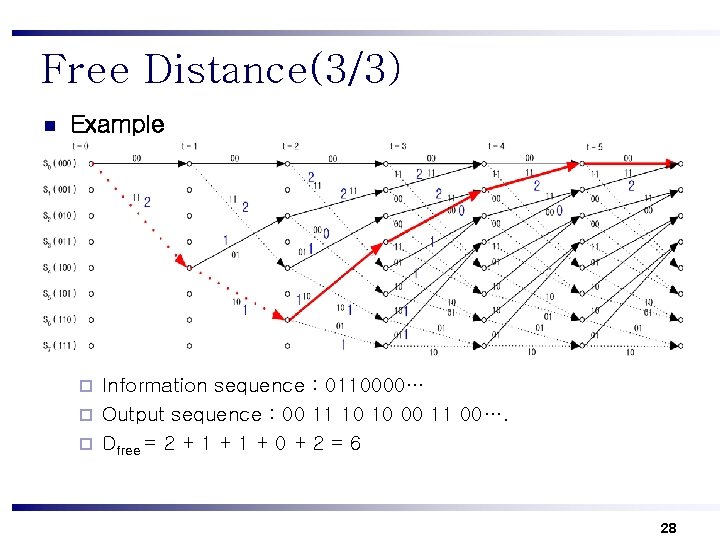
Free Distance(3/3) n Example Information sequence : 0110000… ¨ Output sequence : 00 11 10 10 00 11 00…. ¨ Dfree = 2 + 1 + 0 + 2 = 6 ¨ 28

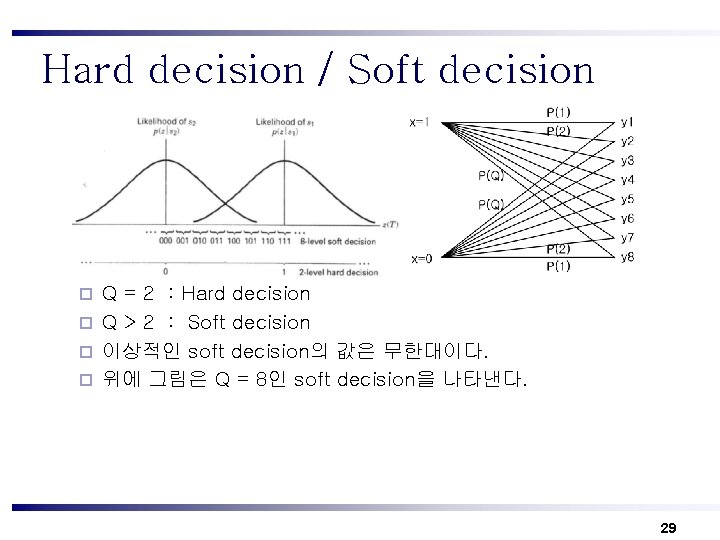
Hard decision / Soft decision Q = 2 : Hard decision ¨ Q > 2 : Soft decision ¨ 이상적인 soft decision의 값은 무한대이다. ¨ 위에 그림은 Q = 8인 soft decision을 나타낸다. ¨ 29

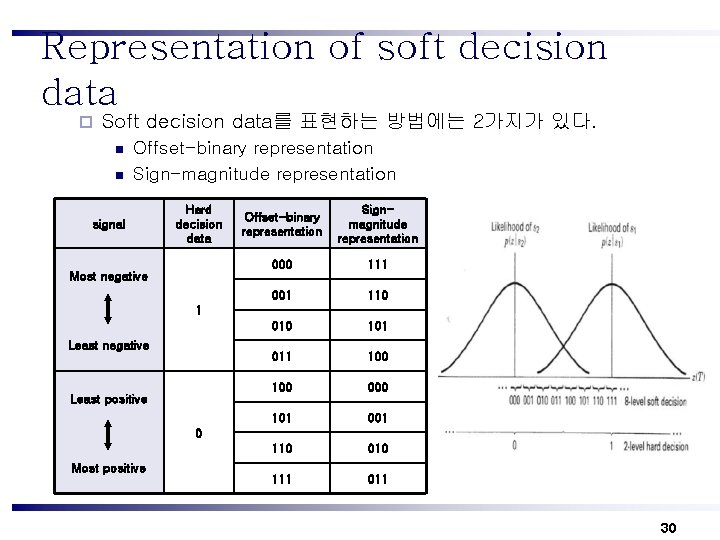
Representation of soft decision data ¨ Soft decision data를 표현하는 방법에는 2가지가 있다. n n Offset-binary representation Sign-magnitude representation signal Hard decision data Most negative Offset-binary representation Signmagnitude representation 000 111 001 110 010 101 011 100 000 101 001 110 010 111 011 1 Least negative Least positive 0 Most positive 30

Application of Convolution Codes(1/2) ¨ Constraint length K = 5 (m = 4) n n n ¨ Constraint length K = 6 (m = 5) n n n ¨ (a) Generator polynomials : ( 23, 35 ) (b) dfree = 7 GSM system (a) Generator polynomials : ( 65, 57 ) (b) dfree = 8 (c) IS-54 american digital cellular system Constraint length K = 7 (m = 6) n n n (a) Generator polynomials : ( 133, 171 ) (b) dfree = 10 Most satellite communication system 31

Application of Convolution Codes(1/2) ¨ Constraint length K = 9 (m = 8) n n n ¨ (a) Generator polynomials : ( 753, 561 ) (b) dfree = 12 IS-95 CDMA system( forward channel ) Constraint length K = 9 (m = 8) n n n (a) Generator polynomials : ( 557, 663, 711 ) (b) dfree = 18 IS-95 CDMA system( reverse channel ) 32

Viterbi Decoder(1/2) n Convolutional codes의 복호화 방법 ¨ Sequential decoding n n n ¨ Code tree 에 서 정확한 경로를 찾아가는 시행 착오적인 방법 탐색상태의 수는 constraint length 와 무관 Sequential decoding, Fano algorithm, stack algorithm 탐색 되는 state metric수가 random 변수 잘못된 가정과 역방 탐색의 예상 수 채널 SNR 함수 계산량의 다양 성을 때문에 도착되는 sequence 들을 저장하기 위해 buffer사용 Threshold decoding n n 낮은 부호 이득 가장 간단한 decoding hardware 33

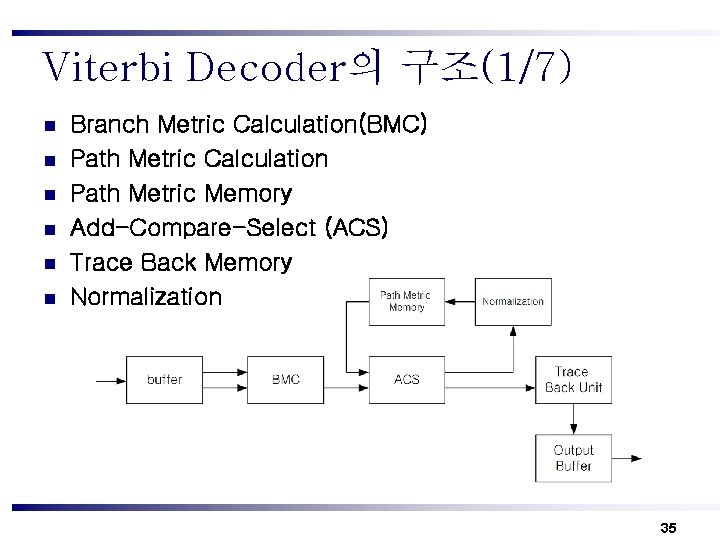
Viterbi Decoder의 구조(1/7) n n n Branch Metric Calculation(BMC) Path Metric Calculation Path Metric Memory Add-Compare-Select (ACS) Trace Back Memory Normalization 35

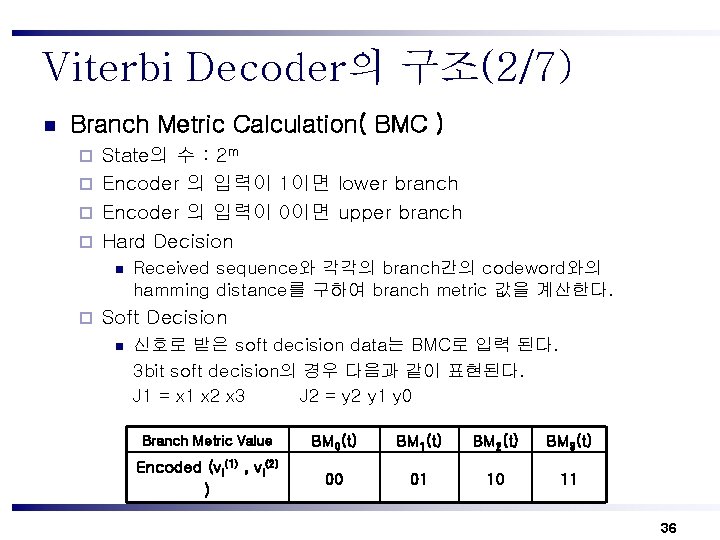
Viterbi Decoder의 구조(2/7) n Branch Metric Calculation( BMC ) State의 수 : 2 m ¨ Encoder 의 입력이 1이면 lower branch ¨ Encoder 의 입력이 0이면 upper branch ¨ Hard Decision ¨ Received sequence와 각각의 branch간의 codeword와의 hamming distance를 구하여 branch metric 값을 계산한다. Soft Decision n 신호로 받은 soft decision data는 BMC로 입력 된다. 3 bit soft decision의 경우 다음과 같이 표현된다. J 1 = x 1 x 2 x 3 J 2 = y 2 y 1 y 0 Branch Metric Value BM 0(t) BM 1(t) BM 2(t) BM 3(t) Encoded (vi(1) , vi(2) ) 00 01 10 11 36

Viterbi Decoder의 구조(4/7) n ACS ( Add Compare Select ) 와 Path Metric Memory BMC(Branch Metric Calculate)에서 계산된 branch metric값과 현재상태의 Path metric 값을 이용하여 새로운 path metric 값을 계산한다. ¨ Path Metric의 개수 = state의 개수 = 2 K-1 = 2 m ( K : 구속장 ) ¨ K가 4인 convolutional encoder의 path metric 값은 다음과 같 다. ¨ n n Path metric 개수 = 24 -1 = 8 PM 0(t), PM 1(t), PM 2(t), PM 3(t), PM 4(t), PM 5(t), PM 6(t), PM 7(t) 38

Viterbi Decoder의 구조(5/7) PMi 3(t) = Min{ PMi 1(t-1) + PMi 4(t) = Min{ PMi 1(t-1) + 여기서 (i 1, i 2) , (j 1, j 2) => (i 3, i 4) , (j 3, j 4) => BM 1(t), PMi 2(t-1) + BM 2(t), PMi 2(t-1) + BM 1(t) BM 0(t), PMi 2(t-1) + BM 3(t), PMi 2(t-1) + BM 0(t) ( 2 P, 2 P+1 ) ( P, P+4 ) 단(K=4) } } 39

Viterbi Decoder - Example(1/16) n Example Generation polynomial G = ( 15, 17 ) ¨ Code rate R = ½ ¨ Constraint length K = 4 ¨ Input sequence ( 011000 ) ¨ 42

Viterbi Decoder - Example(2/16) 43

Viterbi Decoder - Example(3/16) ¨t = 0, 1, 2, 3 각각의 branch에 branch metric을 구하고 각각의 node마다 path metric을 구한다 ¨ Branch metric : 수신된 값과 각 branch에서의 천이 값과의 hamming distance를 구한다. ¨ Path metric : 전 단의 path metric + 각 branch에서의 branch metric을 구한다. ¨ 44

Viterbi Decoder - Example(4/16) ¨ t 0 -t 1의 branch metric, path metric n n n ¨ Received seq : branch : S 0 -S 0 : S 0 -S 4 : Path metric : S 0 : 0 + S 4 : 0 + 00 00 11 0= 2= => branch metric : 0 => branch metric : 2 0 2 t 1 -t 2의 branch metric, path metric n n n Received seq : branch : S 0 -S 0 : S 0 -S 4 : Path metric : S 0 : 0 + S 4 : 0 + 11 00 11 0= 2= => => 0 2 branch metric : : 0 2 45

Viterbi Decoder - Example(5/16) n t=4 Received sequence를 이용하여 branch를 구한다. ¨ T 3에서의 path metric 값과 t 3과 t 4사이의 branch metric값을 더 하여 t 4에서의 path metric 값을 구한다. ¨ 각 stage마다 가장 작은 state를 찾아 ¨ 46

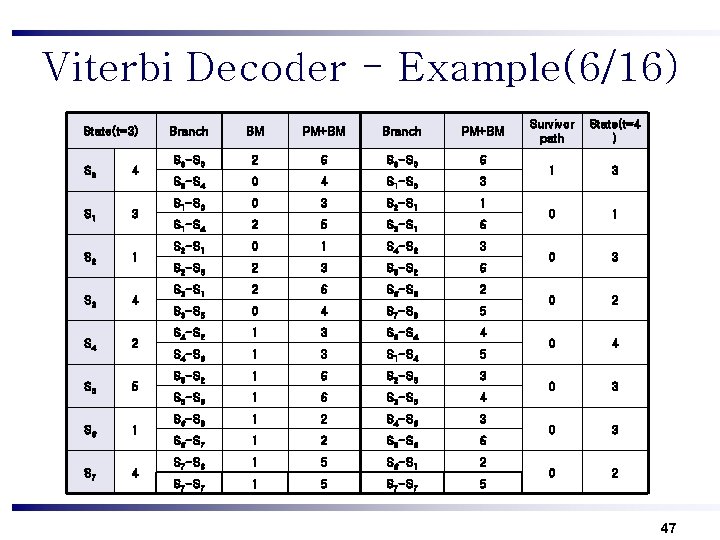
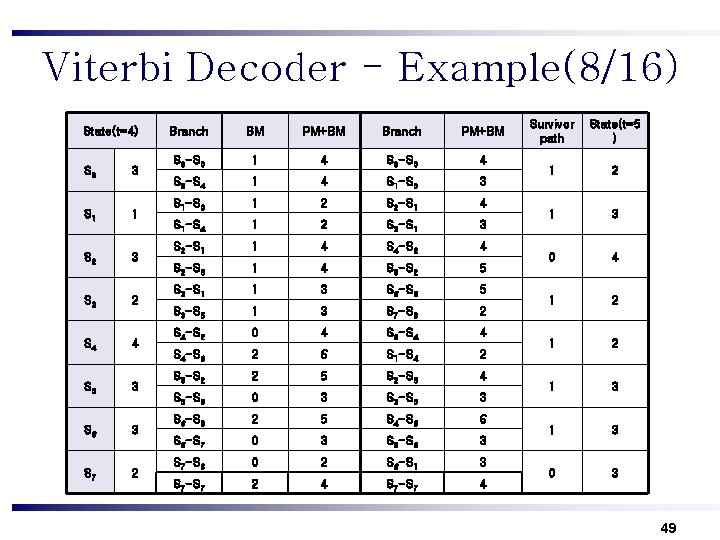
Viterbi Decoder - Example(6/16) State(t=3) S 0 4 S 1 3 S 2 1 S 3 4 S 4 2 S 5 5 S 6 1 S 7 4 Branch BM PM+BM Branch PM+BM S 0 -S 0 2 6 S 0 -S 0 6 S 0 -S 4 0 4 S 1 -S 0 3 S 1 -S 0 0 3 S 2 -S 1 1 S 1 -S 4 2 5 S 3 -S 1 6 S 2 -S 1 0 1 S 4 -S 2 3 S 2 -S 5 2 3 S 5 -S 2 6 S 3 -S 1 2 6 S 6 -S 3 2 S 3 -S 5 0 4 S 7 -S 3 5 S 4 -S 2 1 3 S 0 -S 4 4 S 4 -S 6 1 3 S 1 -S 4 5 S 5 -S 2 1 6 S 2 -S 5 3 S 5 -S 6 1 6 S 3 -S 5 4 S 6 -S 3 1 2 S 4 -S 6 3 S 6 -S 7 1 2 S 5 -S 6 6 S 7 -S 3 1 5 S 6 -S 1 2 S 7 -S 7 1 5 S 7 -S 7 5 Survivor path State(t=4 ) 1 3 0 1 0 3 0 2 0 4 0 3 0 2 47

Viterbi Decoder - Example(7/16) n t=5 48

Viterbi Decoder - Example(8/16) State(t=4) S 0 3 S 1 1 S 2 3 S 3 2 S 4 4 S 5 3 S 6 3 S 7 2 Branch BM PM+BM Branch PM+BM S 0 -S 0 1 4 S 0 -S 0 4 S 0 -S 4 1 4 S 1 -S 0 3 S 1 -S 0 1 2 S 2 -S 1 4 S 1 -S 4 1 2 S 3 -S 1 3 S 2 -S 1 1 4 S 4 -S 2 4 S 2 -S 5 1 4 S 5 -S 2 5 S 3 -S 1 1 3 S 6 -S 3 5 S 3 -S 5 1 3 S 7 -S 3 2 S 4 -S 2 0 4 S 0 -S 4 4 S 4 -S 6 2 6 S 1 -S 4 2 S 5 -S 2 2 5 S 2 -S 5 4 S 5 -S 6 0 3 S 3 -S 5 3 S 6 -S 3 2 5 S 4 -S 6 6 S 6 -S 7 0 3 S 5 -S 6 3 S 7 -S 3 0 2 S 6 -S 1 3 S 7 -S 7 2 4 S 7 -S 7 4 Survivor path State(t=5 ) 1 2 1 3 0 4 1 2 1 3 0 3 49

Viterbi Decoder - Example(9/16) n t=6 50

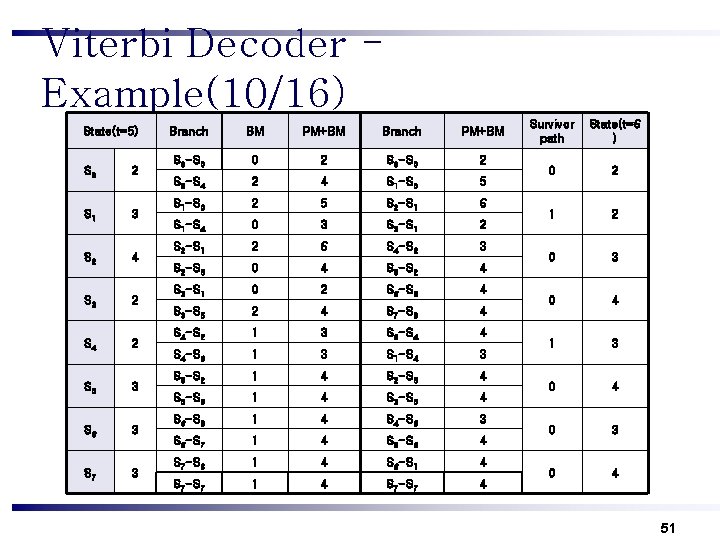
Viterbi Decoder Example(10/16) State(t=5) S 0 2 S 1 3 S 2 4 S 3 2 S 4 2 S 5 3 S 6 3 S 7 3 Branch BM PM+BM Branch PM+BM S 0 -S 0 0 2 S 0 -S 4 2 4 S 1 -S 0 5 S 1 -S 0 2 5 S 2 -S 1 6 S 1 -S 4 0 3 S 3 -S 1 2 S 2 -S 1 2 6 S 4 -S 2 3 S 2 -S 5 0 4 S 5 -S 2 4 S 3 -S 1 0 2 S 6 -S 3 4 S 3 -S 5 2 4 S 7 -S 3 4 S 4 -S 2 1 3 S 0 -S 4 4 S 4 -S 6 1 3 S 1 -S 4 3 S 5 -S 2 1 4 S 2 -S 5 4 S 5 -S 6 1 4 S 3 -S 5 4 S 6 -S 3 1 4 S 4 -S 6 3 S 6 -S 7 1 4 S 5 -S 6 4 S 7 -S 3 1 4 S 6 -S 1 4 S 7 -S 7 4 Survivor path State(t=6 ) 0 2 1 2 0 3 0 4 1 3 0 4 0 3 0 4 51

Viterbi Decoder Example(11/16) n t=7 52

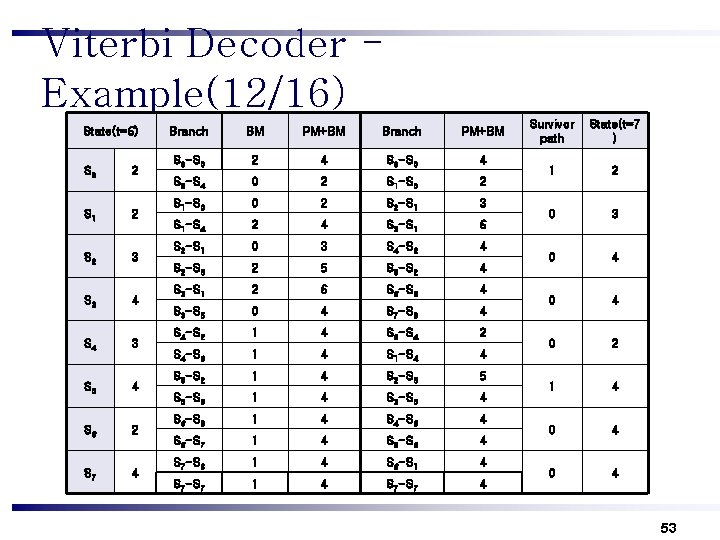
Viterbi Decoder Example(12/16) State(t=6) S 0 2 S 1 2 S 2 3 S 3 4 S 4 3 S 5 4 S 6 2 S 7 4 Branch BM PM+BM Branch PM+BM S 0 -S 0 2 4 S 0 -S 0 4 S 0 -S 4 0 2 S 1 -S 0 0 2 S 2 -S 1 3 S 1 -S 4 2 4 S 3 -S 1 6 S 2 -S 1 0 3 S 4 -S 2 4 S 2 -S 5 2 5 S 5 -S 2 4 S 3 -S 1 2 6 S 6 -S 3 4 S 3 -S 5 0 4 S 7 -S 3 4 S 4 -S 2 1 4 S 0 -S 4 2 S 4 -S 6 1 4 S 1 -S 4 4 S 5 -S 2 1 4 S 2 -S 5 5 S 5 -S 6 1 4 S 3 -S 5 4 S 6 -S 3 1 4 S 4 -S 6 4 S 6 -S 7 1 4 S 5 -S 6 4 S 7 -S 3 1 4 S 6 -S 1 4 S 7 -S 7 4 Survivor path State(t=7 ) 1 2 0 3 0 4 0 2 1 4 0 4 53

Viterbi Decoder Example(13/16) n t=8 54

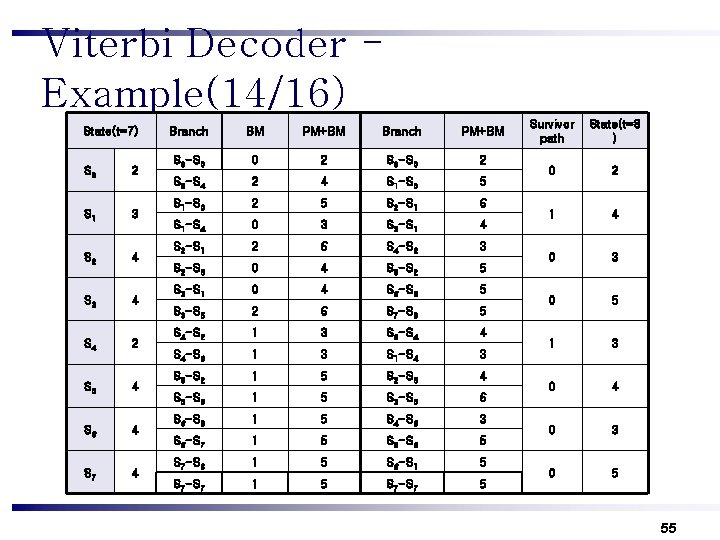
Viterbi Decoder Example(14/16) State(t=7) S 0 2 S 1 3 S 2 4 S 3 4 S 4 2 S 5 4 S 6 4 S 7 4 Branch BM PM+BM Branch PM+BM S 0 -S 0 0 2 S 0 -S 4 2 4 S 1 -S 0 5 S 1 -S 0 2 5 S 2 -S 1 6 S 1 -S 4 0 3 S 3 -S 1 4 S 2 -S 1 2 6 S 4 -S 2 3 S 2 -S 5 0 4 S 5 -S 2 5 S 3 -S 1 0 4 S 6 -S 3 5 S 3 -S 5 2 6 S 7 -S 3 5 S 4 -S 2 1 3 S 0 -S 4 4 S 4 -S 6 1 3 S 1 -S 4 3 S 5 -S 2 1 5 S 2 -S 5 4 S 5 -S 6 1 5 S 3 -S 5 6 S 6 -S 3 1 5 S 4 -S 6 3 S 6 -S 7 1 5 S 5 -S 6 5 S 7 -S 3 1 5 S 6 -S 1 5 S 7 -S 7 5 Survivor path State(t=8 ) 0 2 1 4 0 3 0 5 1 3 0 4 0 3 0 5 55

Viterbi Decoder Example(16/16) Input sequence 0 1 1 1 0 Decoding data 00 11 10 11 01 0 00 11 00 t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 S 0 0 0 1 1 0 Lowest state S 1 0 0 0 1 1 0 1 S 2 0 0 0 0 0 S 3 0 0 0 1 0 0 0 S 4 0 0 0 1 1 0 1 S 5 0 0 0 1 0 S 6 0 0 0 1 0 0 0 S 7 0 0 0 0 0 ¨ Traceback memory안에 저장되어있는 값을 이용하여 최종 decoding data를 구할 수 있다. 57

Convolutional Encoder 설계 n Example Generation polynomial G = ( 15, 17 ) ¨ Code rate R = ½ ¨ Constraint length K = 4 ¨ Input sequence ( 011000 ) ¨ 58

Convolutional Encoder 설계 parameter /*********************************************/ // MODULE : Parameter // // FILE NAME: parameter. v // VERSION: 1. 0 // DATE: FAB 2, 2004 // AUTHOR: DONG KI CHOI // // Description: This file defines a parameter. // /*********************************************/ // defines simulation period `define FULL `define HALF `define PERIOD 20 10 `FULL // defines delay `define DEL 1 // define parmeter `define CONS_K `define DATA_WIDTH `define BUS_WIDTH 4 4 16 59

Convolutional Encoder 설계 – DF. F(1/2) /*********************************************/ // MODULE : D-type flip flop // // FILE NAME: dff_n. v // VERSION: 1. 0 // DATE: JAN 14, 2004 // AUTHOR: DONG KI CHOI // // Description: This module defines a D-type flip flop. // reset is active-low /*********************************************/ `include "parameter. v" module dff_n( clk, rst_n, d, q ); // parameter CARDINALITY = 1; 60

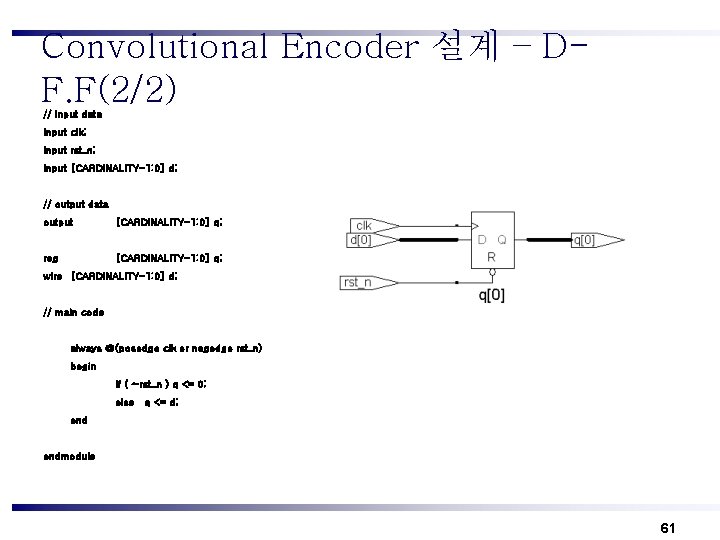
Convolutional Encoder 설계 – DF. F(2/2) // input data input clk; input rst_n; input [CARDINALITY-1: 0] d; // output data output [CARDINALITY-1: 0] q; reg [CARDINALITY-1: 0] q; wire [CARDINALITY-1: 0] d; // main code always @(posedge clk or negedge rst_n) begin if ( ~rst_n ) q <= 0; else q <= d; endmodule 61

Convolutional Encoder 설계 – Convolutional encoder(1/2) /*********************************************/ // MODULE : Convolution encoder // // FILE NAME: convol. v // VERSION: 1. 0 // DATE: JAN 14, 2004 // AUTHOR: DONG KI CHOI // // CODE TYPE: RTL Level // // Description: This module defines a Convolution encoder. // K = 4, generation polynomial = (13, 17), bit rate = 1/2 /*********************************************/ `include "parameter. v" module convol( clk, rst_n, data_in, data_out ); // input data input clk; input rst_n; input data_in; 62

Convolutional Encoder 설계 – Convolutional encoder(2/2) // output data output [1: 0] data_out; wire [`CONS_K-1: 0] poly_a; wire [`CONS_K-1: 0] poly_b; // poly a = 13 // poly b = 17 wire [`CONS_K-1: 0] wa; wire [`CONS_K-1: 0] wb; wire [0: `CONS_K-1] sh_reg; // main code assign dff_n poly_a = 4'b 1011; poly_b = 4'b 1111; df 0( df 1( df 2( df 3( clk clk , , rst_n, data_in, sh_reg[0] ); sh_reg[0], sh_reg[1] ); sh_reg[1], sh_reg[2] ); sh_reg[2], sh_reg[3] ); assign wa = poly_a & sh_reg[0: `CONS_K-1]; assign wb = poly_b & sh_reg[0: `CONS_K-1]; assign data_out[0] = wa[3]^wa[2]^wa[1]^wa[0]; data_out[1] = wb[3]^wb[2]^wb[1]^wb[0]; endmodule 63

Convolutional Encoder 설계 – testbench(1/2) /*********************************************/ // MODULE : test bench-convolution encoder // // FILE NAME: test_conv. v // VERSION: 1. 0 // DATE: JAN 14, 2004 // AUTHOR: DONG KI CHOI // // CODE TYPE: Behavioral Level // // Description: This module defines a test bench convolution encoder. // /*********************************************/ `include "parameter. v" module test_conv(); reg rst_n; reg data_in; reg clk; wire [1: 0] data_out; // main code convol conv (. clk(clk), . rst_n(rst_n), . data_in(data_in), . data_out(data_out) ); always #(`PERIOD/2) clk <= ~clk; initial begin 64

Convolutional Encoder 설계 – testbench(2/2) clk <= 0; rst_n <= 1; #10; rst_n <= 0; #10; rst_n <= 1; data_in <= 0; #`PERIOD; data_in <= 1; #`PERIOD; data_in <= 0; #`PERIOD; $stop; endmodule 65