n list edges and end point vertices gas


























- Slides: 35



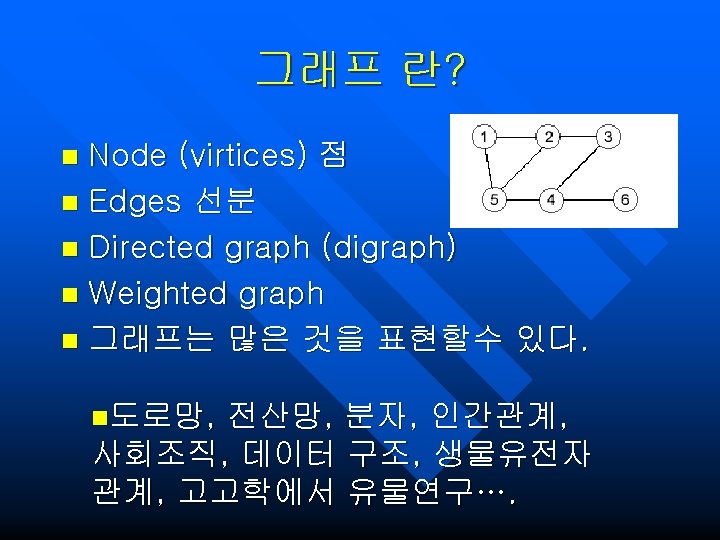
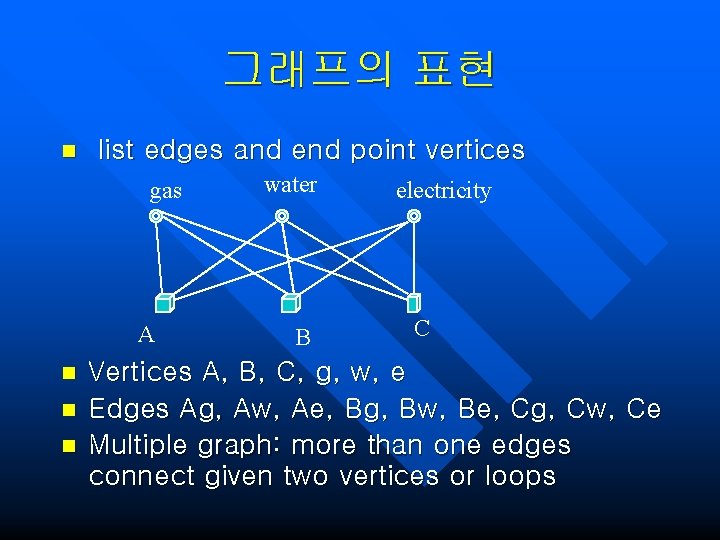
그래프의 표현 n list edges and end point vertices gas A n n n water B electricity C Vertices A, B, C, g, w, e Edges Ag, Aw, Ae, Bg, Bw, Be, Cg, Cw, Ce Multiple graph: more than one edges connect given two vertices or loops

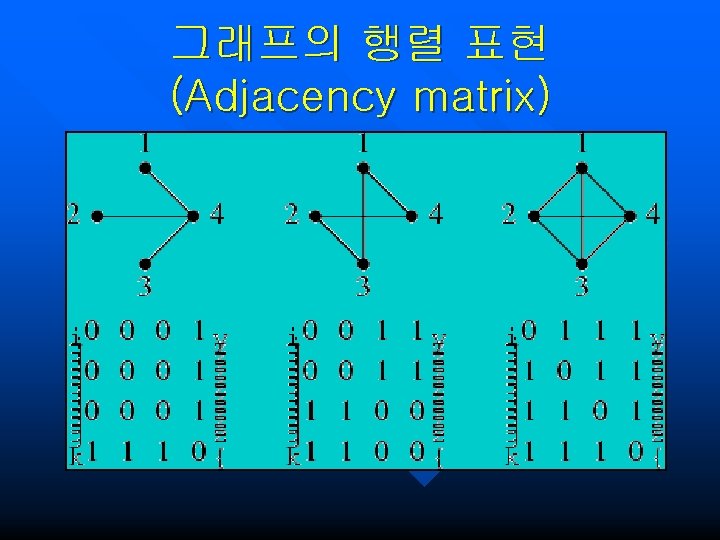
그래프의 행렬 표현 (Adjacency matrix)

Incidence Matrix

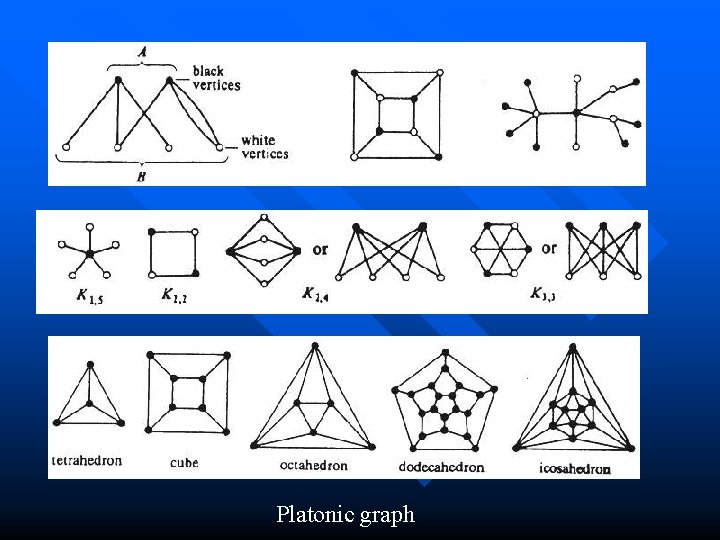
그래프의 종류 Null graph: 연결안됨 n Complete graph: 두점은 반드시 한선분 으로 연결됨 n Cycle graph: single cycle n Path graph: single path n Bipartite graph: vertices into two groups ; complete bipartite graph n

Platonic graph

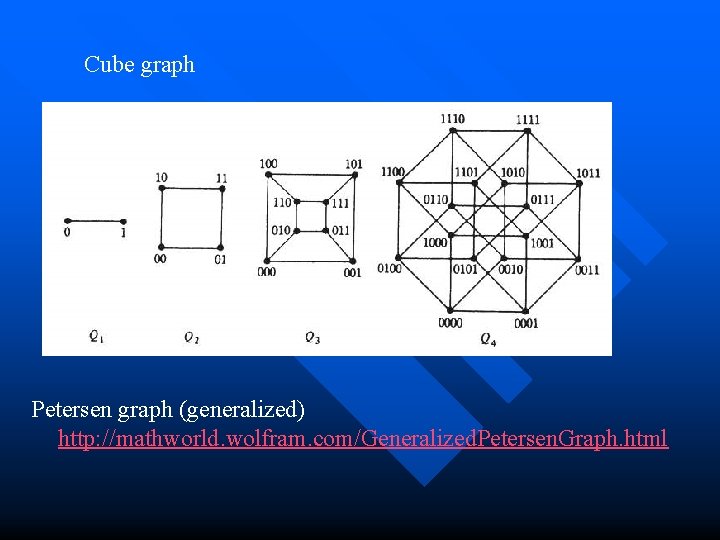
Cube graph Petersen graph (generalized) http: //mathworld. wolfram. com/Generalized. Petersen. Graph. html

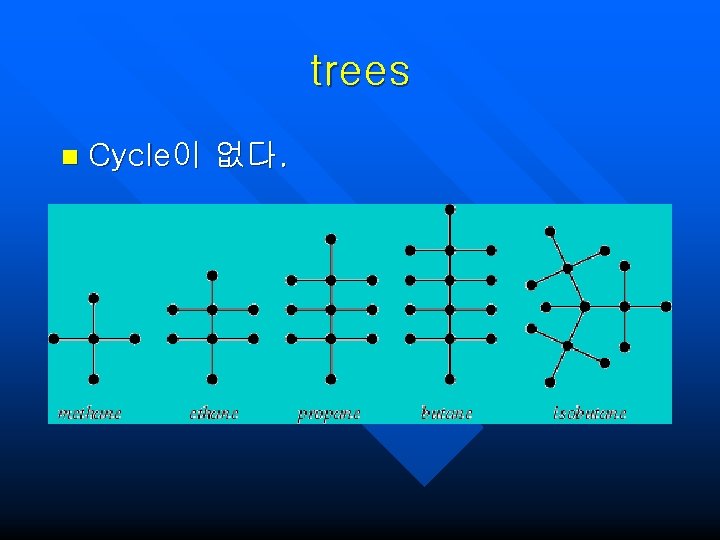
trees n Cycle이 없다.

그래프이론의 주문제 n n n n Euler path problem (Chinese postman problem) Shortest path problem Minimum spanning tree problem Traveling salesman problem Coloring problem (4색문제) Flow problem Isomorphism problems (Graph matching) Canonical Labeling, subgraph isomorphism and monomorphisms, Maximal common subgraph n Graph embedding problem (Planarity)

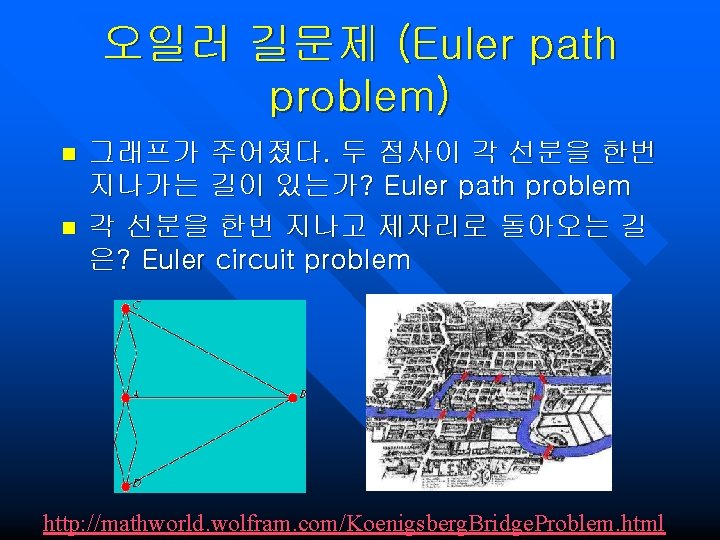
오일러 길문제 (Euler path problem) n n 그래프가 주어졌다. 두 점사이 각 선분을 한번 지나가는 길이 있는가? Euler path problem 각 선분을 한번 지나고 제자리로 돌아오는 길 은? Euler circuit problem http: //mathworld. wolfram. com/Koenigsberg. Bridge. Problem. html

Handshaking Lemma Degree of a node: number of edges ending at a node (no loops) n Handshaking Lemma Sum of all degree is twice the number of edges. n The sum of vertex-degrees are even. n Any graph has an even number of vertices of odd degree n



Fleury's Algorithm n Input: A connected graph G each of whose vertices has an even degree. Output: An Eulerian trail C of G. Method: Expand a trail Ci while avoiding bridges in G-Ci, until no other choice remains.

n n n n Choose and v 0 in V(G) and let C 0=v 0. Set i: =0. Suppose that the trail C=v 0, e 1, v 1, . . . , ei, vi has already been choosen: At vi choose any edge ei+1 that is not on Ci and that is not a bridge of the graph Gi=GE(Ci) unless there is no other choice. Define Ci+1=Ci, ei+1, vi+1. Set i: =i+1. If i=|E(G)|, then halt since C=Ci is the desired circuit; else go to 2. 이 알고리즘은 P일까 NP일까? P

Eulerian Type Problems n Diagram tracing puzzles L. Poinsot 1809 n개의interconnected point n홀 가능 n짝 불가능

Mazes, Labyrinths n http: //www. flint. umich. edu/Departme nts/ITS/crac/maze. form. html Gastron tarry 1895: 이미지나온 교차점으로 가는 길로 가능하면 돌아가지 말라.


Shortest Path Problem Weighted graph가 주어진경우 두점을 연결하고 weight의 합이 최소인 경로찾 기. n http: //en. wikipedia. org/wiki/Dijkstra% 27 s_algorithm n Application to scheduling. n

Spanning tree problem n n A minimum spanning tree is a tree formed from a subset of the edges in a given undirected graph, with two properties: It spans the graph - it includes every vertex in the graph It is a minimum - the total weight of all the edges is as low as possible http: //en 2. wikipedia. org/wiki/Minimu m_spanning_tree

http: //en 2. wikipedia. org/wiki/Kruskal%27 s_algorithm http: //en. wikipedia. org/wiki/Prim's_algorithm

Traveling salesman problem A Hamilitonian cycle: a loop that visits each node once http: //mathworld. wolfram. com/Hamiltonian. Circuit. html NP-Hard http: //www. math. princeton. edu/tsp/

Algorithms for tsp http: //en. wikipedia. org/wiki/Nearest_ neighbour_algorithm n http: //www. pcug. org. au/~dakin/tsp. h tm n

Flows: minmax cut theorem n http: //en. wikipedia. org/wiki/Nearest_ neighbour_algorithm

Coloring problem n The assignment of labels or colors to the edges or vertices of a graph. The most common types of graph colorings are edge coloring and vertex coloring.

Chromatic number X(G): the minimum number of colors for vertex covering of G Chromatic polynomial PG(k): the number of ways to k color. Chromatic index X’(G): the minimum number of colors for edge-coloring of G

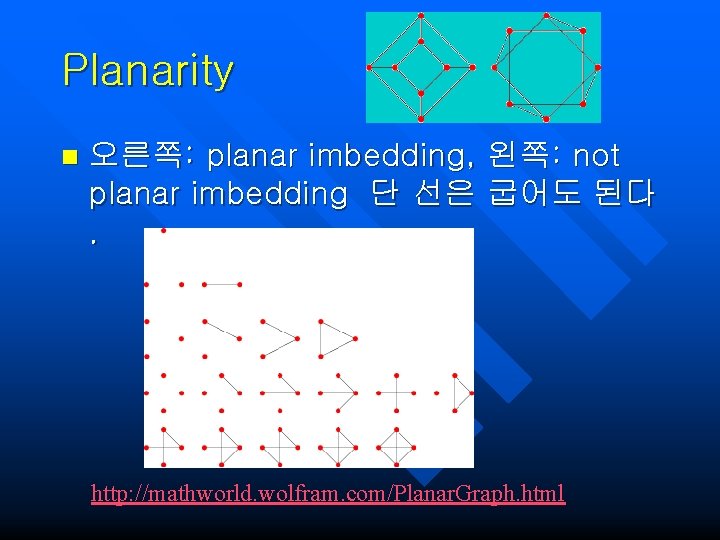
Planarity n 오른쪽: planar imbedding, 왼쪽: not planar imbedding 단 선은 굽어도 된다. http: //mathworld. wolfram. com/Planar. Graph. html

오일러 공식 n G를 연결된 planar 그래프라하자. V: # nodes, E: # edges, F: # regions V – E + F = 2 (주의: 책과 조금 F의 정 의 다름) http: //www. math. ohio-state. edu/~fiedorow/math 655/Euler. html


Kuratowski’s theorem A graph is planar if and only if it does not contain a subdivision of K 5 or K 3, 3. n K 5 는 5개의 node의 complete graph. n K 3, 3 는 6개의 node의 complete bipartite graph. n

4 -color problem n n Guthrie, De Morgan 1852 G a connected planar graph with no bridges. Faces correspond to countries a map

Every map is 4 -colorable. n Equivalent form: every planar graph is 4 -colorable. n Euler’s formula every map contains a digon, triangle, square, or a pentagon. n Kempe’s argument n Final solution: Appel, Haken, (Univ. Illinois) using computer and Heesch’s discharging argument n http: //www-gap. dcs. st-and. ac. uk/~history/Hist. Topics/The_four_colour_theorem. html

Isomorphism problem When is two graph the same? n Connectivity edge connectivity: the smallest number of edges whose removal disconnects G. Vertex connectivity: the above for vertices n Various algorithms n
